电力系统主动解列优化断面的实用化快速搜索方法

苗伟威，雷 鸣，廖大鹏，刘 军，姜 涛

（1.国网山东省电力公司电力调度控制中心，济南 250001；2.天津大学电气自动化与信息工程学院，天津 300072）

电力系统主动解列优化断面的实用化快速搜索方法

苗伟威1，雷 鸣1，廖大鹏1，刘 军1，姜 涛2

（1.国网山东省电力公司电力调度控制中心，济南 250001；2.天津大学电气自动化与信息工程学院，天津 300072）

本文提出一种电力系统主动解列断面的优化搜索方法，以多层图分割理论为框架，通过粗化、初始分区和还原优化3个阶段实现解列断面的快速搜索。结合粗化阶段信息，在还原优化阶段提出一种基于寻优和校验的优化搜索策略，依次进行寻求目标最优解和连通性校验两个过程，借此替代含复杂逻辑约束0-1规划问题的求解，在提高求解效率的同时具有更高的可靠性和可扩展性。为提高拓扑连通性校验效率，提出一种最小化校验子图的构造方法。最后通过两个算例验证了本文方法的有效性。

多层图分割；电力系统主动解列；最小化校验子图；拓扑连通性

Abstract:In this paper，an optimal searching method for the controlled splitting surface in power system is proposed within the framework of multi-level graph partitioning theory.Three stages including coarsening，initial partitioning and refinement are utilized to achieve a rapid search for the splitting surface.Combined with the information in the coarsen⁃ing stage，an optimal searching strategy is proposed in the refinement stage based on optimal searching and verifying in⁃stead of the 0-1 programming with complex logical constraints.With this strategy，optimizing and connectivity-verifying processes are executed sequentially to achieve higher reliability and better extensibility while improving the solving effi⁃ciency.To improve the efficiency in verifying the topology connectivity，a construction method for a minimum sub-graph for verification is proposed.Finally，two numerical examples are used to illustrate the effectiveness of the proposed method.

Key words:multi-level graph partitioning；power system controlled splitting；minimum sub-graph for verification；to⁃pology connectivity

以广域量测系统WAMS（wide area measure⁃ment system）为代表的先进电力技术正不断推动传统输电网向智能电网快速发展[1]，大量可再生能源的接入也使得电网运行方式发生了快速的变化。这些因素都促使着调度运行工作不断转变行为方式，由经验型调度进入到科学型调度模式。对于电网的解列控制，电网运行场景变得更加复杂与多变，传统基于预想场景设定系统解列点的方式适用性不断降低。因此，近年来很多学者开始关注具有协调和智能特征的主动解列方式，并探索出了很多主动解列问题的理论和方法[2-3]。

主动解列是一个涉及到电网运行、控制和保护等多个方面的课题，而该问题的核心是如何快速地确定系统解列方案，使得解列后的子系统各自保持同步运行且最大程度上保持功率供求平衡。上述问题可以看作是图的平衡分割问题，可以利用图论中的相关理论来进行电力系统主动解列问题的研究。例如利用二元决策图[4]、谱分析[5]、k-way[6-7]等方法求解平衡图分割问题，或者将问题转化为最大流最小割问题[8]、含连通拓扑约束的背包问题[9]加以求解，同时还有一部分方法借助于智能优化算法，例如蚁群算法[10]等。

鉴于电力系统庞大的节点数，许多方法在应用时还会受掣于最终简化系统的规模，因此在进行平衡图分割之前要先对原系统进行简化，利用电力系统的部分物理特性，在尽量不影响解列断面搜索的前提下缩减节点规模。例如文献[4，6，11]基于图的等效原理对系统冗余节点进行合并。文献[11-12]分别基于电气距离计算和潮流追踪技术确定发电机和紧密负荷的依附关系从而可对系统进行大幅简化。文献[13]提出一种基于弱联接理论的决策空间预筛方法以有效降低预决策的空间规模。

近年来，图论中大型图划分方法的研究具有重要的参考意义。其中，多层图分割方法通过多次粗化还原过程来保证划分规模和自由度，求解策略可在求取速度和分割质量之间取得较好的平衡[14-17]，在解决图论中平衡图分割这类NP-hard问题时，该方法也被证明是高效和可靠的。而且，在这种解列断面搜索的有效架构[17]下，通过考虑电力系统物理特性和多种启发式逻辑可以进一步提高划分优化效率。

本文沿用多层图分割理论框架，提出一种快速实用的求解方法。在粗化阶段将节点聚合信息有效存储，在还原优化阶段将解列断面的优化搜索分为寻优和校验两个过程，寻优过程筛选出备选方案，校验过程判断子分区是否具有拓扑连通性。其中，校验过程提出一种利用粗化过程节点聚合信息构造最小化校验子图的方法，实现子分区连通性的快速判断校验，提高了断面搜索策略的整体效率。

1 多层图分割理论及还原优化阶段断面优化模型

文献[17]提出的基于多层图分割理论的电力系统主动解列断面搜索方法主要分为粗化、初始分区和还原优化3个阶段，方法如图1所示。首先，在粗化阶段归并节点减小图的规模，直至简化到规模较小的图Gn，快速给出一个较优的初步划分结果。然后在还原优化阶段，逐步将Gn还原到G0，通过恢复节点改善分区结果。

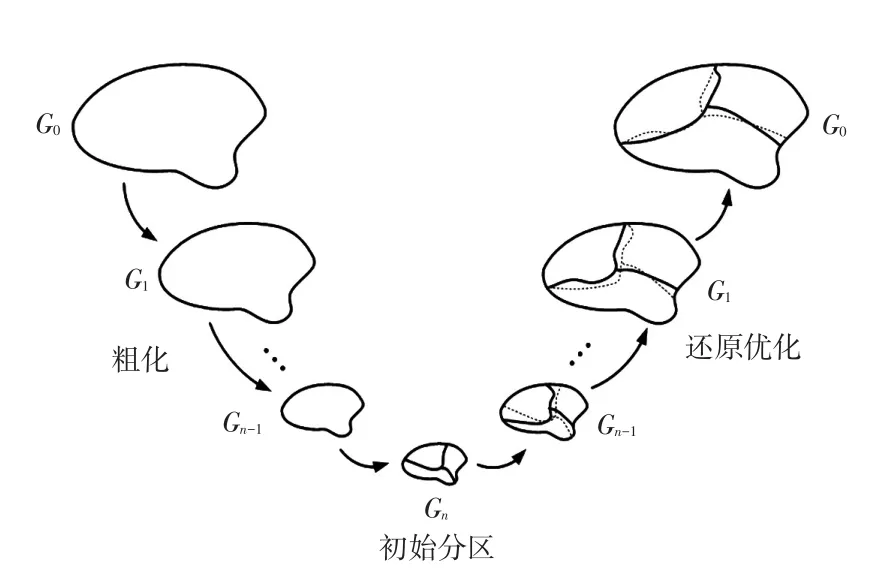
图1 多层图分割理论示意Fig.1 Schematic of multi-level graph partitioning

但是，电力系统的解列断面搜索问题并非是对平衡图分割问题的简单套用，在还原优化阶段要同时考虑解的改进和子分区的连通性。针对还原优化问题，文献[17]给出了1次还原优化过程的求解模型，即

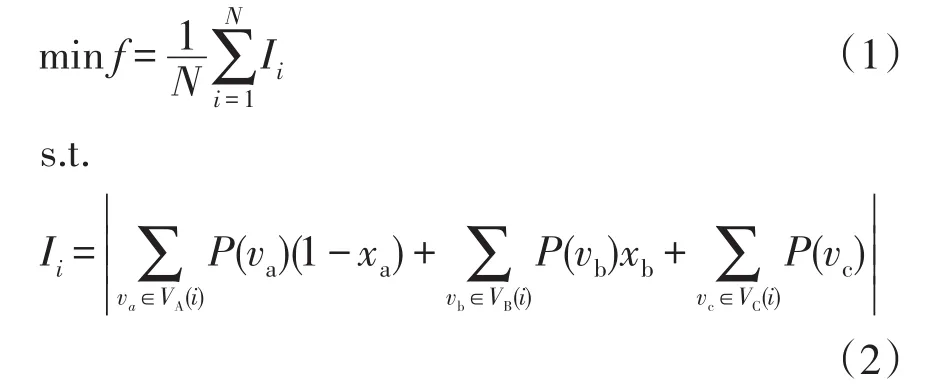
对于所有va∈VA（i），需满足

式中：f为分区功率不平衡度优化的目标值；N为划分的子分区个数；Ii为分区i的功率不平衡度；对应分区i，VA（i）为从相邻分区可能交换至分区i的节点集合，VB（i）为分区i可能交换至其他分区的节点集合，VC（i）为分区i中不参与优化的其余节点集合；对于分区i中任一可能参与交换的节点，定义VSA（i，m）∪VSB（i，m）表示构成该节点与分区i的第m条相连通路所包含的节点集合，其中VSA（i，m）∈VA（i）、VSB（i，m）∈VB（i），相连通路总数记为NS；类似地，定义VRA（i，n）∪VRB（i，n）表示构成该节点与相邻分区的第n条相连通路所包含的所有节点，其中VRA（i，n）∈VA（i）、VRB（i，n）∈VB（i），相连通路总数记为NR；va、vb、vc、vsa、vsb、vra、vrb表示集合VA（i）、VB（i）、VC（i）、VSA（i，m）、VSB（i，m）、VRA（i，n）、VRB（i，n）中的节点；xa、xb、xsa、xsb、xra、xrb为待求0-1变量，表示节点va、vb、vsa、vsb、vra、vrb的交换状态，等于0表示该节点通过割集支路交换到相邻分区，等于1表示留在原分区；xˉ表示对x取反；P（va）、P（vb）、P（vc）为节点va、vb、vc的功率注入，发电为正，负荷为负。

式（1）和式（2）描述了断面优化的目标，即各分区功率不平衡量绝对值之和最小。式（3）和式（4）构造了必要的连通性逻辑约束，由于分区的边界节点都有可能被交换，则需要保证最终可行解满足以下条件：①参与优化的节点若未被交换，则至少需要与原分区保留一条相连通路；②若被交换，则需要与相邻分区存在至少一条相连通路。

2 还原优化问题的快速求解策略

式（1）～式（4）构造了一个完整的考虑连通性约束的边界优化模型，模型可以看作包含多个逻辑约束的0-1规划问题。对该问题的直接求解是可行的，一方面，系统网架结构的稀疏性决定了参与计算的割集边界节点数目并不会随系统规模的扩大明显增大，能够保持在一个较小的范围内；另一方面，通过求解发现多个逻辑约束的加入可以减小寻优空间，进而提高求解效率。通过调用商业软件（例如GAMS的sbb计算软件包）直接求解的求解时间是ms级，计算速度可以接受。

但考虑边界优化问题的实际特点，本文提出了一种实用的快速求解策略替代0-1规划的求解，进一步提高求解效率，其整体流程如图2所示。

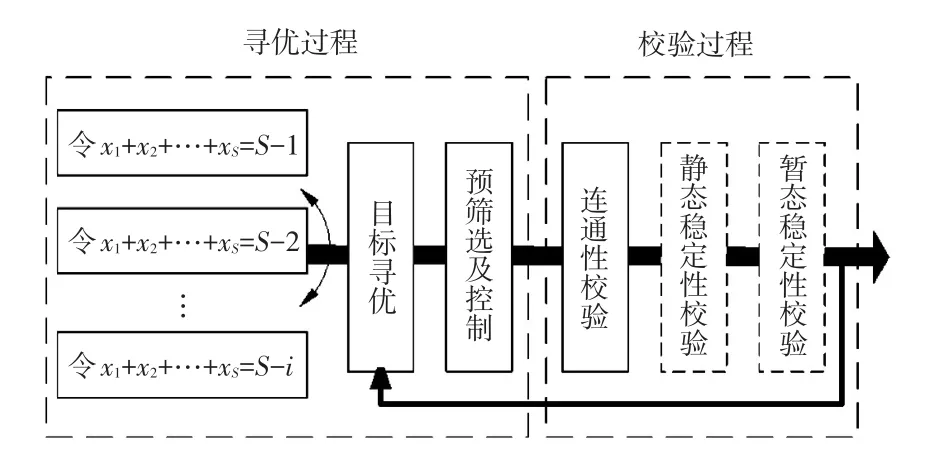
图2 基于寻优、校验过程的求解策略Fig.2 Solving strategy based on optimal searching and verifying

图2给出了一种基于寻优和校验的求解策略，流程分为策略寻优和校验两个过程，寻优过程对应式（1）和式（2），拓扑搜索校验对应式（3）和式（4）。假设规划问题具有S个变量，则寻优过程可分为S个子问题。在不考虑拓扑连通约束的情况下加入约束条件x1+x2+…+xS=S-i(i=1,2,…,S)，其中待求变量x的含义同式（2），约束条件表示该子问题仅允许i个节点交换。通过目标寻优将待校验的结果依次送入校验模块对连通性、静态、暂态稳定性等进行校验，未通过校验时返回寻优过程再将次优解依次送入校验环节直至得到满足校验约束的最优解。该策略有以下3个特点。

（1）在寻优过程中，不含拓扑约束的各子问题计算简单，变量规模较为有限。同时，因为节点权重往往具备足够的多样性，一般不需要交换大量节点来改善优化解。通常完成i≤4的子问题可得到最优解或者相当接近最优解的结果。而且该方法各子问题之间互相并行，适合于采用并行技术加快计算速度。

（2）在还原优化阶段，连通拓扑约束是强制约束，这是潮流收敛和电网稳定的基础，保证拓扑连通性是可行解的必要条件。

（3）设置预筛选和控制模块，预筛选模块中存放当前通过校验的最优解，如果待校验子问题的最优解未能优于目前最优解，则直接忽略校验。此外，还可以扩展定制一些简单的筛选逻辑，提前终止某些无效解的校验进而实现快速识别。例如，部分交换节点通过调整后直接变为孤立节点等。如果在线环境对计算时间有严格要求，那么控制模块可设置最大等待时间（或迭代次数），当计算时间（迭代步数）超过设定值时，终止各进程并比较输出当前最优可行解，其至少是一个满足连通拓扑约束的改进解。

由此可以看出，通过该求解策略可以在实际中有效地求解具有复杂约束的0-1规划问题。与优化算法相比，该策略在取得理想结果时可以不考虑收敛性问题，可以对计算时间和流程进行良好控制，同时也便于与其他校验模块（例如潮流、静暂态分析等）进行衔接，具有良好的可扩展性。但是，该策略要求连通性的校验必须具有较高的效率。下面本文结合粗化和还原阶段提出一种最小化校验子图的检验策略来提高校验阶效率。

3 最小化校验子图构造及校验方法

连通性校验的主要任务是对不同分区的节点进行拓扑，以保证归在同一分区内的所有节点构成一个连通图[18-21]。从搜索量上来看，每次校验搜索的范围是图中的所有节点，对于节点规模较大的网络，以这种形式进行校验显然是不合适的。考虑到该问题的具体特点，优化过程仅仅是边界节点，其他节点的拓扑关系并未受到影响。因此本文考虑利用粗化过程中形成的聚合节点来替代分散的各个节点参与拓扑搜索，聚合节点本身是一个连通子图，以此为代表参与拓扑搜索忽略了其内部节点间的拓扑关系，可大大减少了节点数量，提高搜索的效率。图3描述了利用聚合节点构造最小化校验子图的方法。

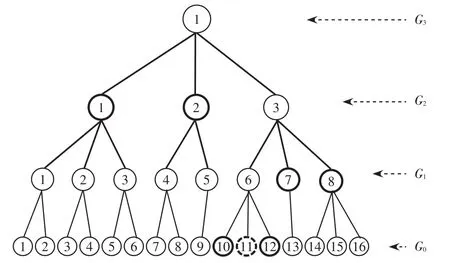
图3 粗化阶段的节点聚合信息Fig.3 Node-clustering information in coarsening stage

图3中自下而上可以理解为粗化过程，而自上而下可以理解为还原过程。原始图G0在粗化过程中，节点数不断变少，直至初始划分阶段图G2仅剩余3个节点。还原过程是粗化的逆过程，粗化过程图G2、G3中的聚合节点本身便是一个连通子图。

图3中节点用符号vi，j来表示，vi，j为图Gi中的节点j。假设图G0已有初步分区结果，寻优过程给出的优化解为移动节点v0，11，节点v0，11在图3中以虚线节点表示，可知节点v0，11在节点v1，6中的局部拓扑结构发生了变化，进而导致v1，6与邻近节点的局部拓扑结构发生了变化，其他节点间的关系未受影响。因此，未受影响的范围应尽可能使用包含节点数最大的聚合节点，从而构成一个节点规模最小的校验子图。具体可通过以下步骤来实现：

（1）创建一个空容器用来存放需要参加连通性校验的节点，同时将所有节点的可添加标志符置1；

（2）以变动节点为起点发起一次深度优先搜索，从叶节点一直寻找到根节点，将过程中搜索到节点的可添加标志符置0；

（3）由根节点开始发起一次广度优先搜索，将可添加标志位为1的节点放入容器中，同时停止搜索标志位为1的节点的子节点，对标志位为0的节点递归采用广度优先搜索，直至搜索到标志位为1的子节点。

按照上述步骤通过一次正向的深度优先搜索和一次逆向的广度优先搜索，便可将需参与校验的聚合节点构成最小校验子图。

由图3可知，移动节点v0，11需要校验的最小化校验子图仅包含节点v2，1、v2，2、v1，7、v1，8、v0，10、v0，11、v0，12等7个节点，除v0，11外，其他节点在图3中以粗实线节点标出。节点v0，11与邻近节点间的拓扑关系并未简化或忽略，然而节点数目却减少了50%以上，而且随着节点规模的扩大，需交换节点的比例占全部节点的比例变低，说明本搜索方法的优势会更加显著。

另外，为了保证构造最小化校验子图的效率，在图的粗化过程中应同时完成高效节点聚合信息结构的存储，即在每个对象（聚合节点）生成过程中完成关联结构的构建，父辈及子辈的指针、支路的对应关系等应有效存储在各节点对象中，以便在访问子辈及父辈时可直接通过内存寻址完成。在步骤（3）的逆向广度优先搜索过程中也可同时完成连通性的校验，这里不再赘述。

4 算例验证

本文通过新英格兰系统和IEEE118节点测试系统两个算例来说明所提方法的有效性，使用C++编制相关程序，并在Intel Dual 2.0GHz CPU，2G RAM计算机环境下测试。

4.1 算例1

算例1首先以新英格兰10机39节点系统为例阐述本文所提出的解列断面搜索方法，该系统包含10台发电机，总发电容量5 107 MW，具体网架结构如图4所示。这里假设由WAMS得到的同步机群分别为{30，37，38，39}和{31，32，33，34，35，36}，两个机群之间因严重故障失步，以此为基础搜索相应的解列断面。

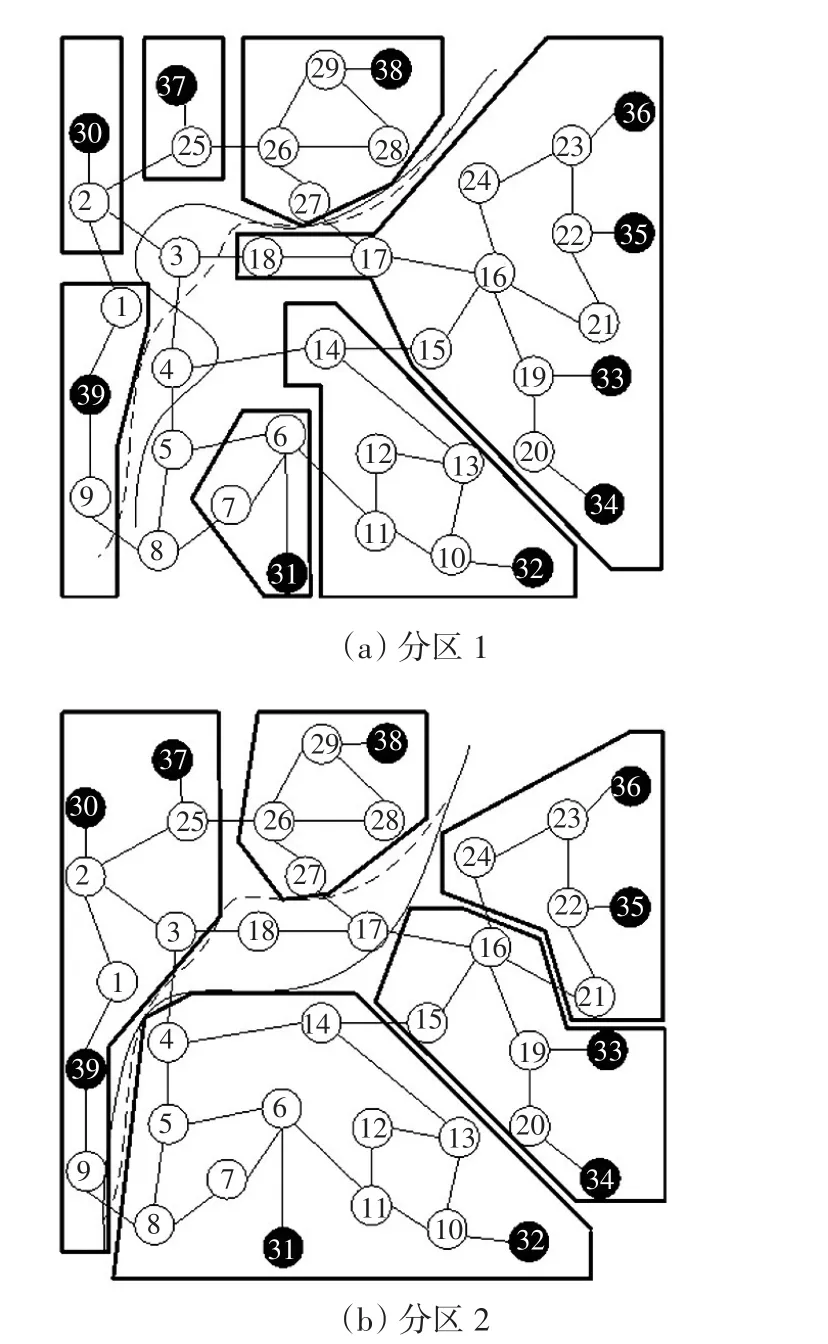
图4 新英格兰测试系统的解列断面优化说明Fig.4 Illustration of splitting surface optimization on New England test system

图5为39节点系统由G0→G6的粗化过程，即节点聚合的过程。由G0→G6依次将节点规模由39下降至23、15、8、4、2、1。由于算例较为简单，本文仅执行最后一次还原优化过程以说明本文方法，还原至初始图G0后，初始解列断面如图4中虚线所示。此时，两个分区的不平衡度及边界节点权重如表1所示，其中正表示发电，负表示负荷。

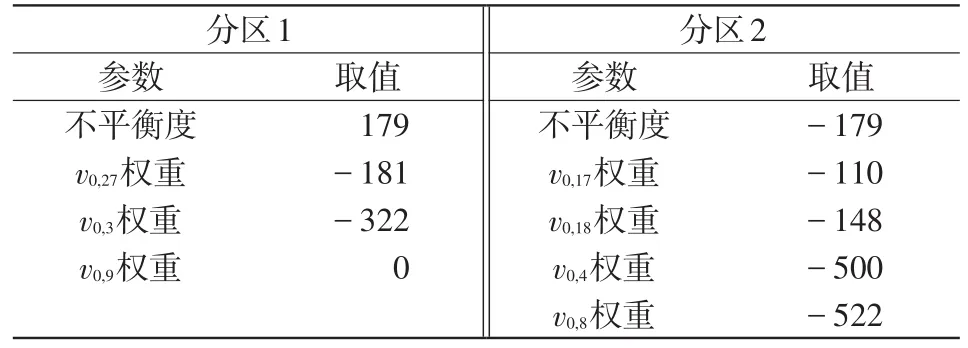
表1 子分区不平衡度及边界关联节点权重Tab.1 Imbalance of partition and the weight of relative nodes next to the boundary

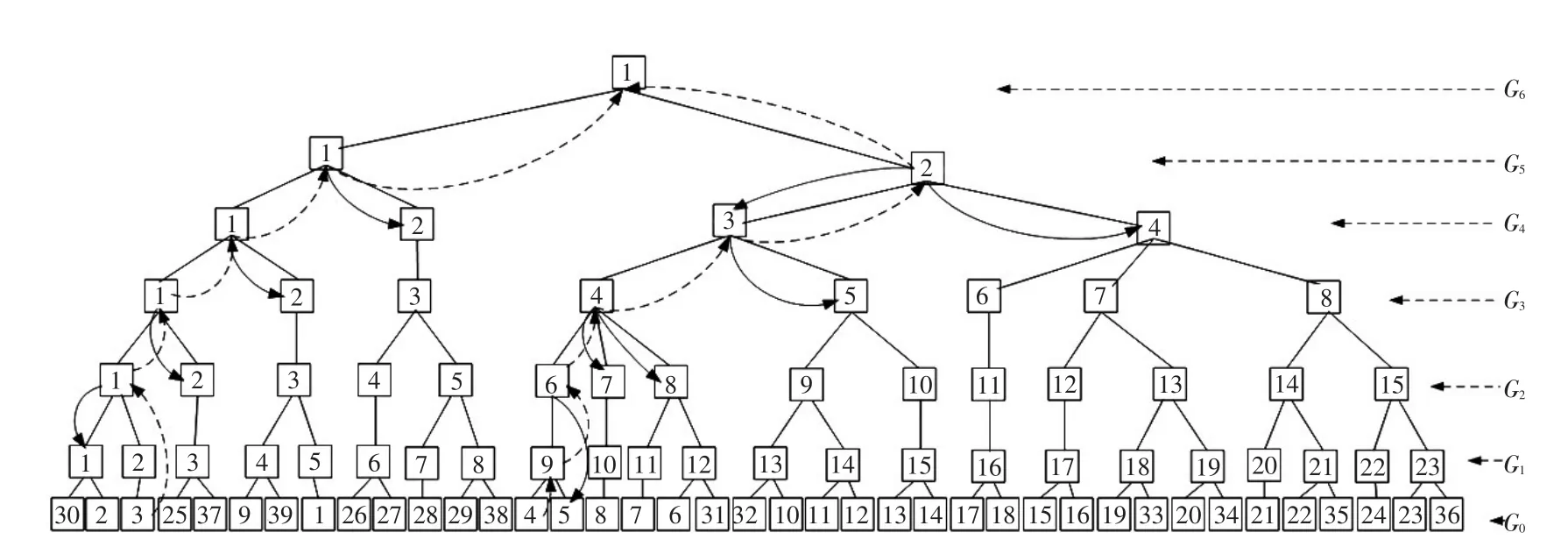
图5 最小化校验子图A的构造过程Fig.5 Construction process of minimum subgraph A for verification

当不考虑拓扑约束时，寻优过程的最优解为节点v0，3、v0，4交换分区，如图4（a）中的实线断面所示，目标不平衡度降至1，进一步通过校验过程检查其拓扑连通性。

按照最小化校验子图的构造方法，由于节点v0，3、v0，4是被移动节点，图5中虚线给出了从起点v0，3、v0，4寻至根节点v6，1的路径。虚线连接的节点表示其部分拓扑结构发生了变化，实线表示逆向搜索过程，实线箭头指向的节点表示其拓扑结构未发生变化，可直接代表其所聚合的节点进入校验子图。通过图5的搜索过程得出的最小化校验子图记为校验子图A，其包含11个节点，具体节点构成如图4（a）所示，其中聚合节点通过框线标出。通过对图4（a）的连通性校验可发现，节点v0，3、v0，4交换分区并非一个可行解，v0，4被交换后与左侧分区不存在连接通路。

寻优过程的出的次优解将节点v0，17、v0，18交换至分区1，如图4（b）中的实线断面所示，调整后子分区的不平衡度为49。与上一步的校验过程类似，最小化校验子图的搜索过程如图6中虚线及实线所示，最终参与校验的校验子图记为校验子图B，节点数为7个，具体接点构成如图4（b）所示。调整后各子系统均为连通子图，因此将v0，17、v0，18交换至分区1为满足连通拓扑约束的最优解。

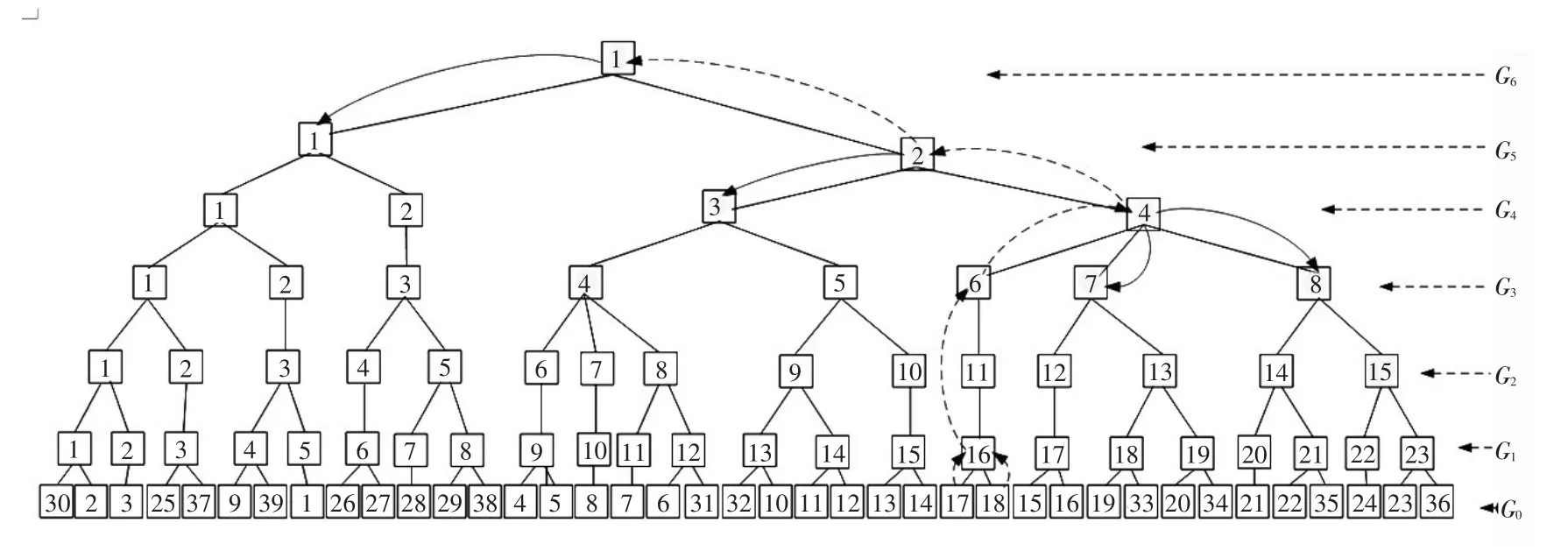
图6 最小化校验子图B的构造过程Fig.6 Construction process of minimum subgraph B for verification

4.2 算例2

算例2以IEEE118节点系统为例对所提出的方法进一步验证。系统接线如图7所示，该系统的总发电负荷约为3 800 MW，发电机失稳模式为机群{10，12，25，26，31，49，54，59，61，65，66，69，80}对机群{87，89，100，103，111}失稳，以此为基础进行解列断面搜索。

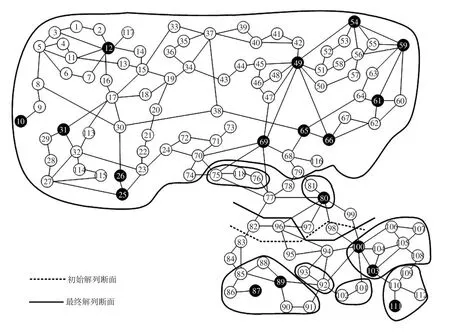
图7 IEEE 118节点测试系统的解列断面优化Fig.7 Splitting surface optimization on IEEE 118-node test system

表2为最后一次优化过程的解列断面及不平衡度变化，初始解列断面如图7中虚线所示，初始分区的不平衡度为61.22，寻优过程给出的最优解为将节点v0，82，v0，96、v0，98交换，不平衡度可降至1.17。由于两个分区的连接关系较为简单，通过本文方法构造的最小校验子图仅包含19个节点，规模与图G0的初始规模（118节点）相比大大减小，聚合节点通过图7中的框线标出。对图7进行校验可知，该解为最优可行解，继续通过后续的还原优化过程无法继续改善该结果，最终的解列断面即如图7中实线断面所示。通过IEEE118节点算例测试本文方法的优化校验过程耗时小于1 ms，证明了方法的有效性。

表2 优化前后的解列断面及分区不平衡度变化Tab.2 Splitting surface before and after optimization and the change of imbalance degree of partition

4 结语

本文沿用多层图分割理论框架，通过粗化、分区和还原优化3个阶段完成电力系统主动解列断面的搜索。考虑电力系统解列问题的具体要求，着重讨论了子图的连通拓扑约束。通过寻优和校验两个过程进行边界的还原优化，避免了含复杂逻辑约束的0-1规划问题的求解，在提高求解效率的同时具备更好的可靠性和扩展性。在图的粗化过程有效存储节点的聚合信息，并利用该信息构造一个用于连通性校验的最小化校验子图，该子图不改变与边界有关的拓扑关系，但节点规模大幅降低，进一步提高了断面优化搜索的效率。通过算例证明了本文方法的有效性。

[1]崇志强，戴志辉，焦彦军（Chong Zhiqiang，Dai Zhihui，Jiao Yanjun）.典型广域保护通信网络的信息传输可靠性评估（Information transmission reliability assessment of com⁃munication network in typical wide area protection）[J].电力系统及其自动化学报（Proceedings of the CSU-EP⁃SA），2014，26（4）：20-24．

[2]高鹏，王建全，甘德强，等（Gao Peng，Wang Jianquan，Gan Deqiang，et al）.电力系统失步解列综述（Review on power system out-of-step separation）[J].电力系统自动化（Automation of Electric Power Systems），2005，29（19）：90-96．

[3]宋洪磊，吴俊勇（Song Honglei，Wu Junyong）.基于广域量测信息的电力系统主动解列控制研究综述（A sum⁃marization of research on wide-area measurement informa⁃tion based power system controlled islanding）[J].电网技术（Power System Technology），2013，37（12）：3467-3474.

[4]Sun Kai，Zheng Dazhong，Lu Qiang.Splitting strategies for islanding operation of large-scale power systems using OBDD-based methods[J].IEEE Trans on Power Systems，2003，18（2）：912-923．

[5]杨健，唐飞，廖清芬，等（Yang Jian，Tang Fei，Liao Qing⁃fen，et al）.基于半监督谱聚类的最优主动解列断面搜索（An optimal controlled partitioning scheme based on semi-supervised spectral clustering algorithm）[J].电网技术（Power System Technology），2015，39（1）：242-249．

[6]Xu Guangyue，Vittal Vijay.Slow coherency based cutset determination algorithm for large power systems[J].IEEE Trans on Power Systems，2010，25（2）：877-884．

[7]Yang Bo，Vittal Vijay，Heydt Gerald T，et al.A novel slow coherency based graph theoretic islanding strategy[C]// IEEE Power Engineering Society General Meeting.Tam⁃pa，USA，2007．

[8]Wang Xiaoming，Vittal Vijay.System islanding using mini⁃mal cutsets with minimum net flow[C]//IEEE PES Power Systems Conference&Exposition.New York，USA，2004．

[9]林济铿，王旭东，李胜文，等（Lin Jikeng，Wang Xudong，Li Shengwen，et al）.基于含连通图约束的背包问题的图分割方法（Graph partition method based on connected graph constraints knapsack problem）[J].中国电机工程学报（Proceedings of the CSEE），2012，32（10）：134-141．

[10]王乙斐，唐飞，廖清芬，等（Wang Yifei，Tang Fei，Liao Qingfen，et al）.带连通性约束的蚁群优化算法主动解列断面求解策略（Controlled splitting surface searching strategy based on ant colony optimization algorithm under connectivity constraints）[J].电力系统及其自动化学报（Proceedings of the CSU-EPSA），2016，28（9）：56-62．

[11]吴学娟，沈沉，向学军，等（Wu Xuejuan，Shen Chen，Xiang Xuejun，et al）.主动解列策略求解过程中的网络化简（Network simplification for active splitting strategy searching）[J].中国电机工程学报（Proceedings of the CSEE），2008，28（7）：7-12．

[12]Wang C G，Zhang B H，Hao Z G，et al.A novel real-time searching method for power system splitting boundary[J].IEEE Trans on Power Systems，2010，25（4）：1902-1909．

[13]乔颖，沈沉，卢强（Qiao Ying，Shen Chen，Lu Qiang）.大电网解列决策空间筛选及快速搜索方法（Islanding de⁃cision space minimization and quick search in case of large-scale grids）[J].中国电机工程学报（Proceedings of the CSEE），2008，28（22）：23-28．

[14]Hendrickson B，Leland R.A multilevel algorithm for parti⁃tioning graphs[R].Albuquerque：Sandia National Labora⁃tories，1993．

[15]Karypis G，Kumar V.A fast and high quality multilevel scheme for partitioning irregular graphs[J].SIAM Journal on Scientific Computing，1998，20（1）：359-392．

[16]Karypis G.METIS：A software package for partitioning un⁃structured graphs，partitioning meshes，and computing fillreducing orderings of sparse matrices version 5.0[EB/OL].http：//glaros.dtc.umn.edu/gkhome/views/metis，2012.

[17]苗伟威，贾宏杰，田圳（Miao Weiwei，Jia Hongjie，Tian Zhen）.电力系统主动解列断面的快速搜索方法（A fast partitioning method for power system controlled splitting）[J].电力系统自动化（Automation of Electric Power Sys⁃tems），2013，37（12）：24-30．

[18]Gao Bo，Yang Yuhang，Ma Huiye.An effective distributed approximation algorithm for constructing minimum con⁃nected dominating set in wireless and Hoc networks[C]// The Fourth International Conference on Computer and In⁃formation Technology.Wuhan，China，2004：658-663．

[19]Kernighan B W，Lin S.An efficient heuristic procedure for partition graphs[J].Bell System Technical Journal，1970，49（2）：291-308．

[20]尹专，刘天琪，江东林，等（Yin Zhuan，Liu Tianqi，Jiang Donglin，et al）.含风力发电的配电网计划孤岛搜索方法（Search method for international islanding of distribu⁃tion network with wind power generation）[J].电力系统及其自动化学报（Proceedings of the CSU-EPSA），2013，25（1）：142-147．

[21]Fiduccia C M，Mattheyses R M.A linear time heuristic for improving network partitions[C]//ACM IEEE Nineteenth Design Automation Conference Proceedings.Las Vegas，USA，1982：174-181．

Practical and Rapid Searching Method for Controlled Splitting Surface Optimization in Power System

MIAO Weiwei1，LEI Ming1，LIAO Dapeng1，LIU Jun1，JIANG Tao2
（1.Dispatch and Control Center，State Grid Shandong Electric Power Company，Jinan 250001，China；2.School of Electrical and Information Engineering，Tianjin University，Tianjin 300072，China）

TM77

A

1003-8930（2017）09-0122-07

10.3969/j.issn.1003-8930.2017.09.020

2015-07-13；

2017-05-25

苗伟威（1985—），男，博士，工程师，研究方向为电力系统运行、稳定与控制，大规模新能源集成。Email：miaowei⁃wei@tju.edu.cn

雷 鸣（1974—），男，硕士，高级工程师，研究方向电力系统运行分析。Email：leiming@sd.sgcc.com.cn

廖大鹏（1974—），男，硕士，高级工程师，研究方向电力系统运行分析。Email：liaodapeng@sd.sgcc.com.cn