基于LMD_SVD的矿山微震与爆破信号特征提取分析
2017-09-29何玉凤
何玉凤


摘 要:针对矿山微震与爆破信号难以识别的问题,提出一种基于局部均值分解(LMD)和奇异值分解(SVD)的微震信号特征提取方法。首先对矿山微震信号和爆破信号进行LMD分解,将多分量的调频信号分解成一系列頻率由高到低的乘积函数(PF)分量;其次,借助相关系数和方差贡献率筛选出包含信号主要信息的PF分量;最后利用SVD计算所选的PF分量构成矩阵奇异值,以此作为区分矿山微震与爆破信号的特征向量。实验结果表明,LMD和SVD相结合的特征提取方法能准确、有效地提取矿山微震和爆破信号特征,为信号识别研究提供了一种新方法。
关键词:局部均值分解;奇异值分解;微震信号;方差贡献率;特征向量
DOI:10.11907/rjdk.172237
中图分类号:TP301 文献标识码:A 文章编号:1672-7800(2017)009-0028-04
Abstract:A method of microseismic signal feature extraction based on local mean decomposition (LMD) and singular value decomposition (SVD) is proposed for the identification of microseismic and blasting signals in mines. Firstly,the mine microseismic signal and blasting signal are decomposed by LMD, and the FM multi-component signal is decomposed into a series of frequency from high to low product function (PF) components; secondly, the PF component contains the main information signal are selected by correlations and variance contribution ratios . finally the singular values of selected PF component matrix are calculated by SVD, which are used as a characteristic vector to distinguish the microseismic and blasting signals of the mine.The experimental results show that the feature extraction method combined with LMD and SVD can accurately and effectively mine the characteristics of microseismic and explosion signals, and provides a new method for signal recognition research.
Key Words:local mean decomposition; singular value decomposition; microseismic signal; variance contribution rate; feature vector
0 引言
矿山微震信号容易受到外界干扰,在干扰因素中,人工爆破震动源较难识别。国内外研究者在矿山微震与爆破信号的识别方面作了大量探索,主要包括多参数分析法和频谱分析法。
微震信号由于具有非平稳、非线性特征,利用传统信号分析方法处理较为困难。关于微震信号的特征提取,姜福兴等[1]提出基于“初步判断”、“联合判断”和“优化判断”的微震单事件多通道特征提取与联合识别方法;董陇军等[2]选取微震“能量对数”、“信号主频”等作为Fisher分类的特征值。这些多参数分析法提取的特征参数比较复杂且实现较为困难;赵毅鑫等[3]采用傅里叶变换对微震频谱特征进行分析,但是傅里叶变换只能对微震信号作初步识别;朱权洁等[4]借鉴地震学理论,采用小波包分析技术,对爆破震动与岩石破裂波形在多频带内的能量分布差异进行了对比研究。小波与小波包都是将微震信号划分到特定频带,对信号的自适应分解性较差;吴响等[5]采用经验模态分解(EMD)将原信号分解,利用Volterra级数对分解后的本征模态分量(IMF)建立非线性预测模型,提取模型参数作为特征向量;尚雪义[6]提出了基于EMD和SVD的矿山信号特征提取及分类方法,将主要IMF构成矩阵的奇异值作为表征微震信号的特征向量。但是EMD分解存在过包络、欠包络和端点效应等问题,影响了提取的特征向量。
鉴于此,本文建立基于LMD_SVD的微震信号特征提取模型:首先采用LMD分解得到矿山微震与爆破信号的PF分量,然后借助相关系数和方差贡献率筛选出包含信号主导的PF分量,最后利用SVD分解由主要的PF分量构成矩阵奇异值,将此作为识别微震信号的特征向量。本文方法不仅解决了参数分析法提取的特征参数较复杂的问题,还消除了EMD分解过程中存在的过包络和端点效应等现象,能更有效地提取矿山微震和爆破信号的特征向量。
1 基本理论
1.1 局部均值分解(LMD)方法
局部均值分解是一种新的自适应非平稳信号的处理方法,该方法将一个复杂的非平稳初始信号x(t)分解成k个PF分量和uk(t)(其中uk为残余项)之和。LMD分解与Huang等[7]提出的EMD分解类似,均会出现虚假分量,真实分量与原始信号具有较强相关性,而虚假分量由误差造成,相关性很弱。分量的方差贡献率可以衡量分量的重要性,其值越大,相应分量越重要[8]。对于PF分量是否为有效分量,本文采用了相关系数和方差贡献率进行筛选,各PF分量与原始信号的相关系数和方差贡献率越大,其对应的PF分量越重要。具体定义如式(1)、(2)所示。c(i)=∑nj=1(x(j)-x)(PFi(j)-PFi)∑nj=1(x(j)-x)2·(∑nj=1(PFi(j)-PF)2)endprint
(1)
v(i)=1n∑nj=1PFi(j)2-1n∑nj=1PFi(j)2∑ni=11n∑nj=1PFi(j)2-1n∑nj=1PFi(j)2
(2) 式中c(i)为PFi与原始信号的相关系数,v(i)为PFi的方差贡献率,n为信号的总采样点数。
1.2 奇异值分解(SVD)
SVD是一种矩阵分解和变换技术,在信号处理和数据压缩方面应用广泛。设原始信号的采样点个数为n,真实的PF分量个数为m,则可以构造m×n阶的矩阵X。X的SVD如式(3)所示。X=USVT=∑ri=1σiuivTi
(3) 式中U、V分别为m×m和n×n阶的正交矩阵,S为m×n阶的斜对角矩阵(S=σ0
00,其中σ=diag(σ1,σ2,σ3,…,σr)),σi(i=1,2,3,…,r)为矩阵的奇异值,并且σ1≥σ2≥…≥σr≥0。
由上式可知,矩阵X也可看作特征向量ui,vTi作外积之后与奇异值σi的加权和,权重即为非零的奇异值,权重越大,相应的特征向量在重建信号中所占比例则越大。因此,以奇异值构建的特征向量能有效地反映变换矩阵X,也能反映信号的本质特征,故可用奇异值实现对微震信号的数据降维和特征提取的目的。
2 基于LMD_SVD的微震信号特征提取
本文提出的基于LMD_SVD的微震信号特征提取方法主要消除了EMD分解出现的端点效应等问题,而且提取的特征参数较为简单。主要包括如下步骤:
第一步:为了减小信号幅值对LMD分解的影响,先对原始信号进行归一化处理,得到归一化后的信号x*(t)=x(t)/xmax(t)。
第二步:对信号x*(t)进行LMD分解,得到一系列按照频率由高到低的PFi(i=1,2,…,n)分量。
第三步:利用相关系数和方差贡献率选取信号主导的j个PF分量,剔除虚假PF分量,得到真实的PF分量,构成特征矩阵X=[c′1,c′2,…,c′4]T。
第四步:对特征矩阵X进行SVD分解,得到矩阵的奇异值σi(i=1,2,3,…,r),此奇异值作为表示微震信号的特征向量。
第五步:分别求出同时测量的N个样本的奇异值,并计算各对应奇异值的均值,比较平均奇异值之间的关系,判断其作为微震信号特征值的可行性。
3 實例分析
处理微震数据的关键是从微震监测系统接收到的信号中识别出有效的微震事件,而其中干扰最多的就是爆破震动。为了有效识别矿山微震和爆破信号,本文选取某矿山两种信号进行对比分析,信号的采样频率为1 000Hz,采样点数为5 000。
3.1 频谱特性分析
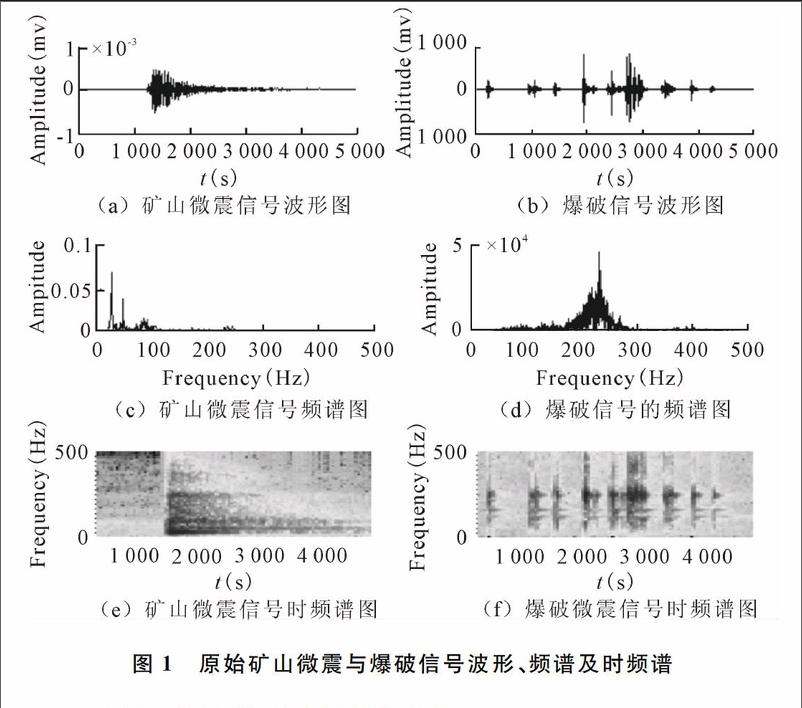
微震检测系统采集的信号一般为时序信号,对信号进行频谱分析可以将信号描述从时域转换到频域,进而分析信号的频率成分及特征,其波形、频谱图以及时频谱图如图1所示。
分析图1的信号波形图可知,矿山微震信号表现为连续单一的形态,并且波动持续时间较长,起振与衰减过程较为缓慢;爆破信号表现为单个信号中有多个相似的波形形状。由频谱图可知,微震信号的频率分布比较集中,主要集中在20~100Hz之间,且主频比较低;爆破信号的频率成分较复杂,分布相对分散,主要在150~300Hz之间,且主频较高,主要在200~300Hz之间。由时频谱图也可知,矿山微震信号能量分布较为密集,而爆破信号能量分布较为分散。从整体上看,矿山微震的主频比爆破信号主频低。
3.2 LMD-SVD微震信号特征提取
为了说明本文提出的方法,对上述选取的矿山微震和爆破信号进行分析。首先对选取的两种信号进行LMD分解,分别得到6个(见图2(a))和7个(见图2(b))PF分量。矿山微震各PF分量的最大振幅分别为0.748 0、0.892 2、0.424 9、0.115 8、0.049 3、和0.015 2;爆破信号各PF分量的最大振幅分别为0.930 5、0.118 2、0.037 5、0.014 0、0.011 8、0.002 9和0.004 2m/s。由此可知,矿山微震和爆破信号的振动强度主要集中在PF1~PF4和PF1~PF2。由式(1)、(2)分别计算各PF分量与原始信号的相关系数和各自的方差贡献率,得到它们与分解层次的关系,如图3所示。分析图3可得如下结论:①微震信号LMD各分量的相关系数与方差贡献率随着分解层数增加,基本上呈现先增加后降低的趋势,且具有很好的正相关,爆破信号随着分解层数增加,整体上呈降低趋势;②微震信号LMD各分量中,PF1~PF3与原始信号的相关系数和方差贡献率较大,而PF4~PF6较小,均小于0.02,爆破信号PF1、PF2的相关系数较大,且PF1的贡献最大,PF3~PF7的相关系数均小于0.01,且PF2~PF7的方差贡献率均小于0.03。因此,LMD的主要分量为PF1~PF4。综上所述,选取PF1~PF4作为SVD分解特征矩阵最为合理。
由图2可知,PF分量包含了多维信息,从微震检测系统中随机抽取矿山微震和爆破事件各7个,并且对每个事件传播距离最近的波形信号进行特征提取。使用按照前述方法筛选得到的PF分量构成特征矩阵X=[c′1,c′2,…,c′4]T,然后进行SVD分解,得到矿山微震和爆破信号奇异值共56个,分别对各奇异值求平均值如图4所示。
由图4可知,矿山微震平均奇异值σ1、σ2较大,而σ3、σ4较小;矿山微震和爆破信号的平均奇异值σ1、σ2、σ4差异较大。由此可以得出,奇异值可以作为识别矿山微震和爆破信号的定量表征。
4 结语
本文围绕矿山微震与爆破信号难以识别的问题,提出了一种基于LMD_SVD的矿山微震和爆破信号特征提取的分析方法。主要结论如下:
(1)借助LMD分解对微震信号进行分析,不仅能够有效分解归一化处理后的原始信号,分解过程中还消除了EMD分解出现的端点效应等问题。endprint
(2)信号的奇异值矩阵反映了信号特征,且矿山微震和爆破信号有不同的奇异值矩阵。通过SVD分解信号主导的PF分量构成的特征矩阵得到奇异值,两种信号奇异值差异较大,故以此作为识别矿山微震与爆破信号的定量表征。该方法的研究为获取微震信号特征提供了一种新思路。
参考文献:
[1] 姜福兴,尹永明,朱权洁,等.单事件多通道微震波形的特征提取与联合识别研究[J].煤炭学报,2014(2):229-237.
[2] 董陇军,孙道元,李夕兵,等.微震与爆破事件统计识别方法及工程应用[J].岩石力学与工程学报,2016(7):1423-1433.
[3] 赵毅鑫,姜耀东,王涛,等.“两硬”条件下冲击地压微震信号特征及前兆识别[J].煤炭学报,2012(12):1960-1966.
[4] 朱权洁,姜福兴,于正兴,等.爆破震动与岩石破裂微震信号能量分布特征研究[J].岩石力学与工程学报,2012,31(4):723-730.
[5] 吴响,钱建生,王海燕,等.微震信号多尺度非线性特征提取与辨识研究[J].仪器仪表学报,2014(5):969-975.
[6] 尚雪义,李夕兵,彭康,等.基于EMD_SVD的矿山微震与爆破信号特征提取及分类方法[J].岩土工程报,2016(10):1849-1858.
[7] HUANG N E, SHEN Z, LONG S R, et al. The empirical mode decomposition and the hilbert spectrum for nonlinear and non-stationary time series analysis[C].Proceedings of the Royal Society of London A: Mathematical, Physical and Engineering Sciences. Great Britain: The Royal Society, 1998:903-995.
[8] 徐鋒,刘云飞.基于EMD-SVD的声发射信号特征提取及分类方法[J].应用基础与工程科学学报,2014(6):1238-1247.
(责任编辑:黄 健)endprint
