基于CUDA的计算架构求解集装箱码头连续泊位分配问题
2017-09-28韦华杨智应
韦华,杨智应
(上海海事大学信息工程学院,上海 201306)
基于CUDA的计算架构求解集装箱码头连续泊位分配问题
韦华,杨智应
(上海海事大学信息工程学院,上海 201306)
具有强大并行计算能力的GPU成为高性能计算的重要平台之一。基于CUDA的计算架构,实现求解线性规划问题的单纯形算法。在此基础上,实现求解整数规划问题的分支定界法,并将它应用于求解集装箱码头连续泊位分配问题。实验结果表明,基于CUDA的计算架构可大大缩短计算时间。
并行计算;GPU;CUDA;单纯形算法
0 引言
并行计算已广泛应用于许多领域。海量的信息及数据蕴藏着无法估量的价值,如何及时高效地分析处理是高性能计算所面临的重要问题。随着计算架构的演进,需求变得多样化、复杂化,并行编程模型也随之动态改变,应用领域也不断地延伸、扩大[1]。从单核到多核再到众核,从串行、单线程到并行、大规模多线程,求解问题的模式的转换,以往的串行编程模型正在被替代。
中央处理器(Central Processing Unit,CPU)有强大的算术运算单元,逻辑运算单元和大容量的缓存。在复杂的逻辑运算方面CPU拥有强大的优势;图形处理器(Graphics Processing Unit,GPU)拥有巨大的浮点计算性能和极高的存储器带宽,与生俱来就拥有大规模并行的处理器核心,在计算密集型及易于并行的程序上具有明显的优势。在浮点处理能力上GPU有强大的优势,低端的GPU能和主流的CPU相媲美,主流的GPU与同期的主流CPU就性能而言,竟能相差10倍左右。
自2006年11月NVIDIA公布了第一个基于CU⁃DA架构的GPU—GeForce 8800 GTX,打破了只能执行传统图形计算的局限,继而使得GPU在通用计算中广泛使用,且获得了令人惊喜的成绩。这也吸引了更多不同领域的学者基于CUDA进行研发,取得了令人瞩目的成绩,不仅在性能上提升了多个数量级,而且就单位成本和能耗与传统的CPU运行程序相比较而言都要低好多[3]。它不仅可以获得计算性能收益,而且可以充分利用能耗,这种基于CUDA的GPU计算将是计算机界的一大里程碑[4]。
线性规划问题是工业生产和经济管理中常见的最优化问题。它由一组线性约束和一个线性目标函数构成。需要求决策变量的值使得目标函数最大化(最小化)。单纯形算法[5]是解决线性规划问题的经典高效算法。它的求解过程是一个不断迭代的过程,直到最优解出现。在迭代的操作中是不断重复换元操作,这一过程能利用并行计算以加快其速度。
求解整数规划问题的分支定界法以单纯形算法为基础。当规模很大时,整数规划的求解是非常费时的。本文基于CUDA的计算架构,实现求解线性规划问题的单纯形算法。在此基础上,实现求解整数规划问题的分支定界法,并将它应用于求解集装箱码头连续泊位分配问题。实验结果表明,基于CUDA的计算架构可大大缩短计算时间。
1 基于CUDA计算架构的单纯形算法的实现
1.1 CCUUDDAA编程模型
虽说GPU的浮点处理能力强于CPU,但是一个完整的CUDA程序,还是离不开CPU的。在CUDA编程模型中,CPU与GPU协调工作、各司其职[4]。作为主机(Host)的CPU负责将部分串行代码完成,及内核函数启动前设备端所需数据的准备及初始化工作;GPU作为设备端(Device)或协处理器,完成并行性的计算。具体功能如下:
(1)Host端完成的功能:启动CUDA、分配内存空间、显存空间及初始化内存数据、利用CudaMemcpy()复制数据到显存、调用内核函数、将结果利用Cu⁃daMemcpy()复制数据到内存、释放空间、退出CUDA。
(2)Device端完成的功能:读数据到GPU片内、处理数据、将结果写回显存。
1.2 基于CCUUDDAA的单纯形算法实现
单纯形算法是一个不断进行迭代的过程,迭代的次数与目标函数非基本变量的系数相关。单纯形算法的基本思想[6]:在与原规划等价的松驰型中,换元操作按照选择标准,选择一个非基本变量作为替入变量和一个基本变量作为替出变量,重写松弛型。然后将非基本变量设为0,求得基本变量的值,得到一个基本可行解,判断重写后的目标函数中非基本变量的系数是否有正数,如有则继续换元迭代,重复上述过程;反之,停止迭代,得到最优解。单纯形算法主要的三个操作是:找到替入变量、替出变量和重写等式。寻找替入变量这一过程并不适宜使用并行计算,寻找替出变量,即是找到最紧约束,首先并行计算得出每个式子的约束,然后并行缩减,得出最近约束,但是可能数据在GPU中读取写入的时间里CPU已经完成了相当数量的工作。因此,这种简单,数据量少的计算不适宜在GPU上执行。重写等式的数据量多且计算量大,在GPU上运行具有明显的优势,所以,本文将重写等式[5]这一操作并行计算。在这一过程中具体的并行过程的核心代码如下:

上述的代码是设备端即内核函数中重要代码。根据替入变量和替出变量的下标,重写线性规划松驰型,约束等式中的非基本变量的系数及常数相应改变,目标函数中的常数及非基本变量的系数也改变。CUDA的每个线程都有自己的线程号Id,通过核函数里的int tid1=blockDim.x*blockId.x+threadIdx.x和 int tid2=block⁃Dim.x*blockIdx.x+threadIdx.x语句,每个线程可以获得自身的Id号,从而找到自己的任务去执行。一个线程执行一个任务后还要继续执行余下未执行的任务,所以通过blockDim.x*gridDim.x这一递增量,让线程知道自己的下一个任务。递增的步长即为线程格中正在运行的线程数量。其中gridDim.x、blockDim.x、threadIdx.x为内建函数,它们代表的含义分别为网格中x轴上块的数量、块中x轴上线程数量、线程所在块(block)中的索引号。
2 集装箱码头连续泊位分配问题建模
集装箱码头泊位分配问题分为离散泊位分配和连续泊位分配[8]。下面简述连续泊位分配模型。
2.1 前提假设
连续泊位分配模型基于以下假设条件:
(1)港口的船舶数、岸线长度、时间周期、桥吊数及每条船的长度、到港时间、作业路数、作业量都是已知的;
(2)泊位岸线的水面深度满足船的吃水深度且泊位是连续的;
(3)将船之间的安全距离算入船舶的长度,允许零距离泊位;
(4)船舶到港后,没有合适的泊位,就等待,直到有合适的泊位,船舶只有一次靠泊机会,且在作业期间,桥吊要一直服务,直到船舶离港;
2.2 连续泊位分配模型
基于以上连续泊位分配模型的假设条件建立以下模型:
目标函数:

TSi为船舶i开始工作的时间;BSi为船舶i开始工作的泊位;WTi为船舶i的工作时间;Li为船舶i的长度;Ti为船舶i的到港时间;CRi为船舶i的工作路数即桥吊数;B、S为岸线长;T为时间周期;A为船的个数;CRS为总的桥吊数;σij表示船i在船j的下方且不重叠即两条船在时间方向上不重叠,则为1,否则为0;δij表示船i在船j的左侧且不重叠即两条船在泊位空间上不重叠,则为1,否则为0。
式(1)表示最小化所有船舶开始泊位工作的时间之和;式(2)保证任意两船不交叠;式(3)表示船舶到港后才可以进泊位分配,开始工作,式(4)表示船舶工作的结束时间不大于T,即所有船舶必须在计划期内完成装卸作业;式(5)表示任意船舶的船头部分不超出总的泊位空间;式(6)表示泊位后,任意船舶的船尾部分不超出总的泊位空间;式(7)表示任意时刻,所有在泊的船的工作路数之和不超过桥吊总数。
在上述模型中,目标函数是一个线性函数,约束条件为线性不等式,它们是一个整数规划问题。刘莉莉等应用分支定界法[8]求解以上整数规划模型。但其编程主要是串行模式,当船舶数量较大时,问题的求解变得很慢,效率较差。为此,本文基于CUDA的计算架构实现求解整数规划问题的分支定界法,并将它应用于求解集装箱码头连续泊位分配问题,以期能大大缩短计算时间。
3 连续泊位分配问题的计算实验
本文实验环境是VS2010+CUDA6.5+NVIDIA Ge⁃Force 610M,文中的实验部分数据是采用文[7]中实现的算例,如5,7,9条船。其中的单纯性算法是基于CUDA而实现,得出如表1的统计结果。当船的数量增加至9条船时,文[8]中的实验时间在4小时以上;而在本文的实验中,9条船的泊位分配策略在数秒内就得以实现了。具体的实验结果如下表1:

表1 基于CUDA的单纯性算法的分枝定界法实验结果与刘的SBB算法实验结果
本文又继续做了实验,以测试基于CUDA的计算架构的性能,11条到港作业船泊的基本信息如下表2所示,在这里 A=11,S=80,T=24,CRS=12。

表2 十一条船舶的基本信息
基于CUDA的计算架构的单纯形算法的分支定界法11条船泊的泊位分配计划信息如图1所示,其中time1即为运行时间。
基于CUDA的单纯形算法的分支定界法的十一条船舶二维直观图泊位分配图如图2所示:
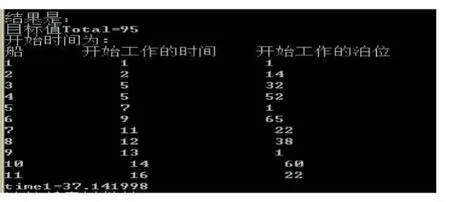
图1 十一条船基于CUDA的单纯形算法的分支定界法泊位分配计划信息图
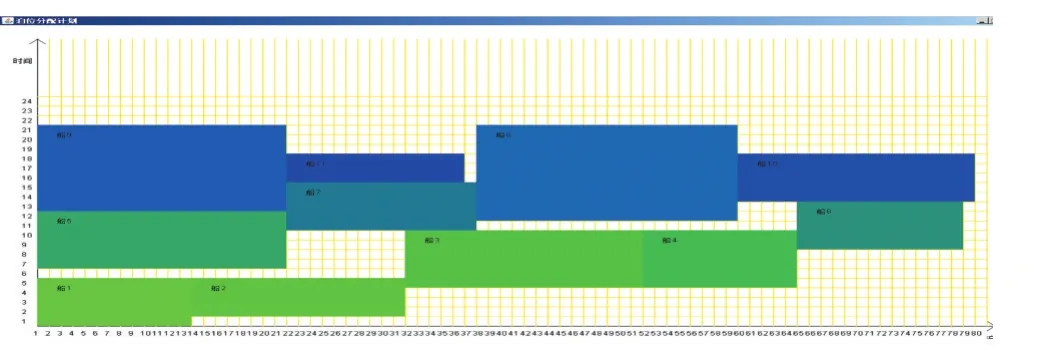
图2 十一条船基于CUDA的单纯形算法的分支定界法泊位分配图
12条到港作业船舶的基本信息如表3所示,在这里 A=12,S=80,T=36,CRS=20。
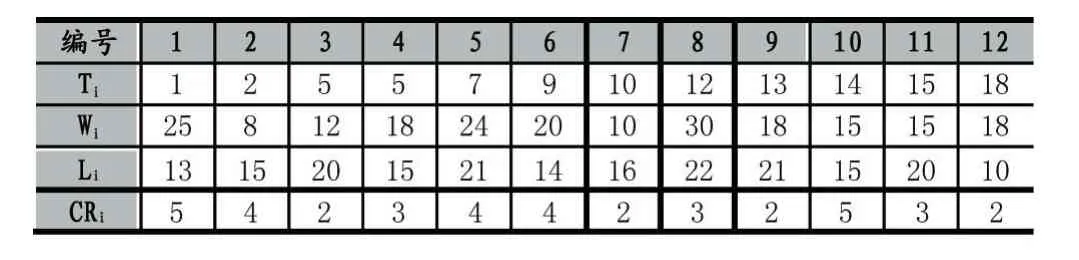
表3 十二条船舶的基本信息
基于CUDA的计算架构的单纯形算法的分支定界法12条船泊的泊位分配计划如下图3所示,其中time1即为运行时间。
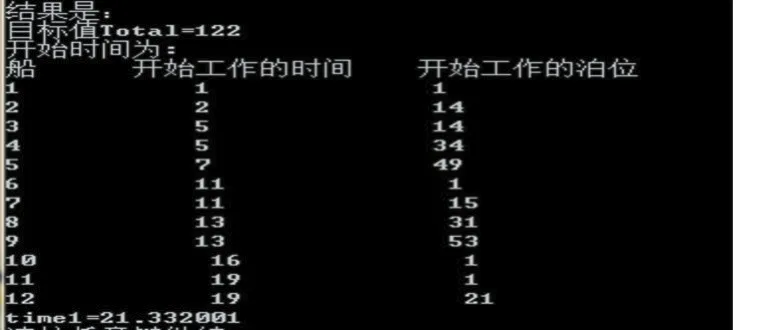
图3 十二条船基于CUDA的单纯形算法的分支定界法泊位分配计划信息图
基于CUDA的单纯形算法的分支定界法的十二条船舶二维直观图泊位分配图如图4所示:
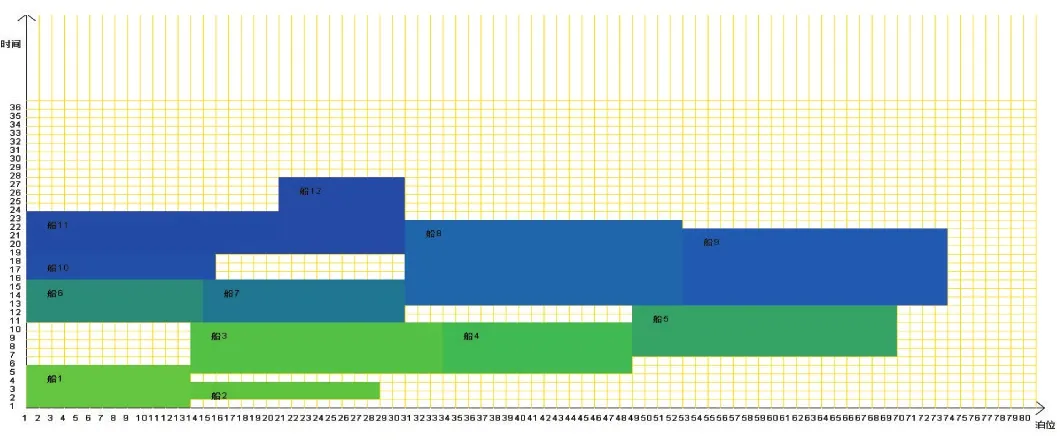
图4 十二条船基于CUDA的单纯形算法的分支定界法泊位分配图
上述实验结果表明,基于CUDA的计算架构能大大缩短连续泊位分配模型的计算时间。文[8]中的实验并没有给出11,12条船舶的实验数据,且在9条船时,实验所用时间就相当的大。本文基于CUDA的计算架构的分支定界法求解连续泊位分配问题,对11和12条船的情况仍然可以在理想的时间里获得泊位分配计划。通过分析实验结果,明显的突出了利用GPU进行并行计算的优势,挖掘出了GPU高性能的特点。
4 结语
本文利用GPU强劲的并行处理能力,基于CUDA的计算架构实现求解线性规划问题的单纯形算法,在此基础上实现分支定界法求解集装箱码头连续泊位分配问题。使得计算时间大大缩短。对提高集装箱港口生产管理效率有着重要的应用价值。本文的后续研究工作将建立一个完善的港口集装箱码头岸边资源分配系统,并将基于CUDA的计算架构计算模式加以应用。
[]金晶,陈山枝.并行计算普适编程模型及系统架构研究[D].北京:北京邮电大学,2012.
[2]Shane Cook.CUDA Programming:A Developer's Guide to Parallel Computing with GPUs[M].苏统华,李东等译.北京:机械工业出版社,2014.1.
[3]Jason Sanders、Edward Kandrot.CUDA By Example:an Introduction to General-Purpose GPU Programming[M].聂雪军等译.北京:北京工业出版社,201.1.
[4]张舒,褚艳利等.GPU高性能运算之CUDA[M].北京:中国水利水电出版社,2009.10.
[5]A Fast Simplex Algorithm for Linear Programming[J].Journal of Computational Mathematics,2010,v.2806:837-847.
[6]Thomas H.Cormen,Charles E.Leisersonet,殷建平等译.Introduction to Algorithm,Third Edition[M].北京:机械工业出版社,2013.1.
[7]吴庆丰.改进的单纯形法迭代计算方法[J].计算机工程与应用,2014,50,No.81718:59-62+69.
[8]刘莉莉,杨智应.集装箱码头连续泊位[D].上海海事大学,2010.
Solution of Container Terminal Berth Allocation Problem Based on CUDA Calculation Architecture
WEI Hua,YANG Zhi-ying
(College of Information Engineering,Shanghai Maritime University,Shanghai 201306)
GPU with the powerful ability of parallel computing is one of the most important platforms for high performance computing.Based on the CUDA computing architecture,realizes the simplex algorithm for solving linear programming problems.On that basis,presents the branch and bound method for solving integer programming problems,which is applied to solve the problem of continuous berth allocation in con⁃tainer terminals.The experimental results show that the computing architecture based on CUDA can greatly reduce the computation time.
1007-1423(2017)23-0017-05
10.3969/j.issn.1007-1423.2017.23.004
韦华(1990-),女,山东菏泽人,硕士,研究方向为并行分布式计算与软件工程
2017-05-04
2017-08-05
Parallel Computing;GPU;CUDA;Simplex Algorithm
