一种改进的SVPWM开关调制方案

华国新

（浙江广厦建设职业技术学院，东阳 322100）

一种改进的SVPWM开关调制方案

华国新

（浙江广厦建设职业技术学院，东阳 322100）

在对PWM控制技术发展现状进行分析的基础上，提出旨在降低电磁干扰的SVPWM控制策略，分析其控制原理，得出SVPWM控制策略优化方案，最后对其进行仿真和实验，结果证明此方案的合理性以及运用的可行性。

软开关；三相逆变器；SVPWM

0 引言

电压空间矢量法（SVPWM）以空间矢量原理为基础，适用于低开关频率调制的级数较高的多电平逆变器。跟一些经典的脉宽调制方式相比具有如下优点：输出电压和电流的THD较低；控制过程较为简单，并易于用DSP芯片实现；开关频率较低[1]。在SVPWM模式下，采用不同的零矢量分配方法及零矢量作用时间，会产生不同的共模干扰电压、输出电压谐波含量和开关损耗[2]，所以采用合适的零矢量分配方案，可以有效降低逆变器的开关损耗，减小共模干扰电压。基于此考虑，本文提出一种改进的空间矢量控制方案，以降低开关损耗，同时减少逆变器的共模干扰。

1 三相逆变器SVPWM控制原理

参见图1，三相逆变器电压空间矢量法（SVPWM）源于交流电机变频传动控制的电压空间矢量PWM控制技术原理图[3]。图1中定义P点电位为VD，Q点电位为0。T1有门极驱动信号VG1时，T4的门极驱动信号VG4=0，T1导通，这时vA0=VD。当T4有门极驱动信号VG4时，T1的门极驱动信号VG1=0，T4导通，这时vA0=0。引用A、B、C桥臂的开关变量为Sa、Sb、Sc，由于Sa、Sb、Sc各有两种状态：0或1，因此整个三相逆变器共有23=8种开关状态。即(Sa、Sb、Sc)为0（0 0 0），1（0 0 1），2（0 1 0），3（0 1 1），

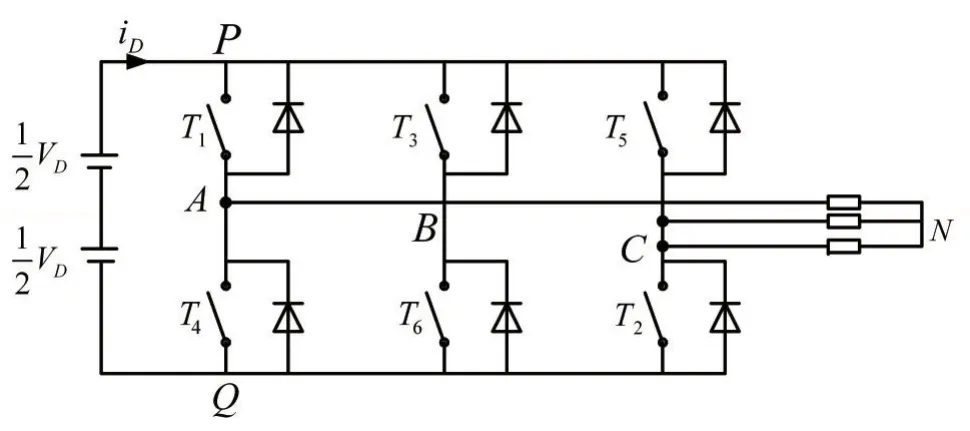
图1 三相逆变器原理图

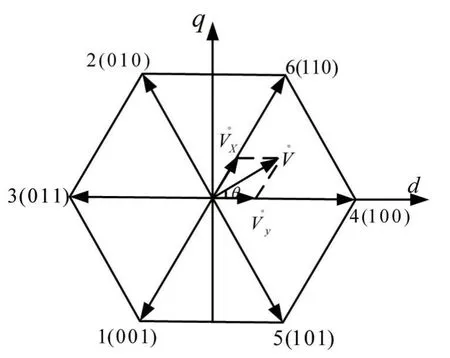
图2 空间矢量

4（1 0 0），5（1 0 1），6（1 1 0），7（1 1 1）[4-6]。上述 8种开关状态被称为状态 0，1，2，3，4，5，6，7。我们只通过上桥壁功率管的开关状态，就可以推算出线电压向量[vAB，vBC，vCA]T及相电压向量[vAN，vBN，vCN]T：

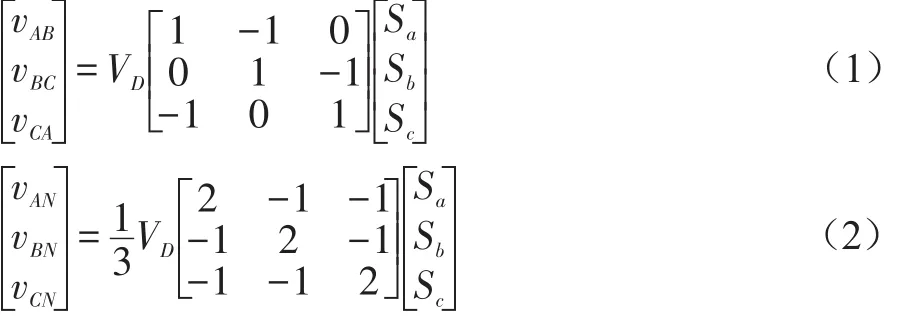
利用三相坐标到两相D、Q坐标的变换公式，可得：

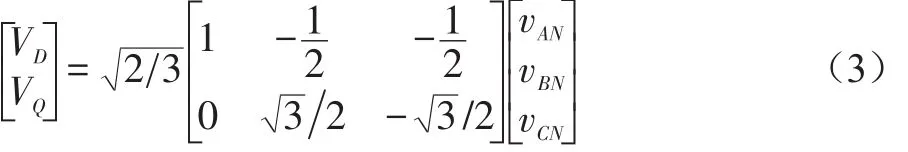
利用两相垂直电压[VD，VQ]T替代三相电压[vAN，vBN，vCN]T，得到两个位于坐标原点的零电压矢量和六个相互夹角为60°的非零电压向量，如图2所示。

若要求 的相位角θ=wt为任意指令值，则矢量可由其所在扇区边界的相邻特定矢量V。X、V。y和零矢量V。Z合成。在很短的一个开关周期TS中，令TX、Ty及T0分别为特定矢量V。X、V。y和零矢量V。Z的存在时间，则任意位置的矢量V。可通过利用逆变器的三个开关状态及一个周期TS中对应的TX、Ty、T0来合成，即：

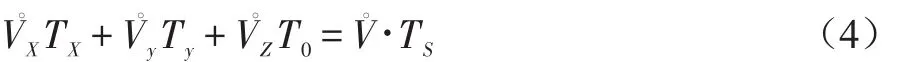
2 优化SVPWM开关调制模式

从式（4）我们可知，参考矢量V。的合成与零矢量V。Z（V0和V7）无关，然而当采用不同的零矢量分配方法时，将形成不同的共模干扰电压、开关损耗和输出电压的谐波含量[8]。由文献[6]可知，采用零矢量产生的共模电压峰值，3倍于其它非零矢量的共模电压峰值。文献[4]中利用其他相位相反的非零电压矢量进行组合，达到与零矢量相同的效果，但减小了共模电压。但该SVPWM控制方法与传统SVPWM相比，在每一次开关状态的改变中需要至少两多个功率器件发生动作[6]。从而引起线电压的半周期内出现反极性的电压脉冲，导致产生转矩脉动。

针对此问题，本文提出一种降低共模电压的空间矢量控制方案，来降低传统SVPWM的共模电压。SVPWM优化开关调制方案控制算法的实现过程可描述为：首先确定参考电压矢量Vref*所在扇区，然后为离参考矢量相邻的四个矢量计算作用时间；最后利用开关电压矢量作用时间合成三相脉宽调制信号[7-8]。

根据三相逆变系统原理，利用α-β坐标系易于实现空间电压矢量调制，故应将三相轴系变换到α-β坐标系[9]。以扇区I为例，利用坐标变换，参考电压矢量Vref*与分量Vα及Vβ的关系如图3所示，得到Vα和Vβ后，实现空间电压矢量调制将大大简化。

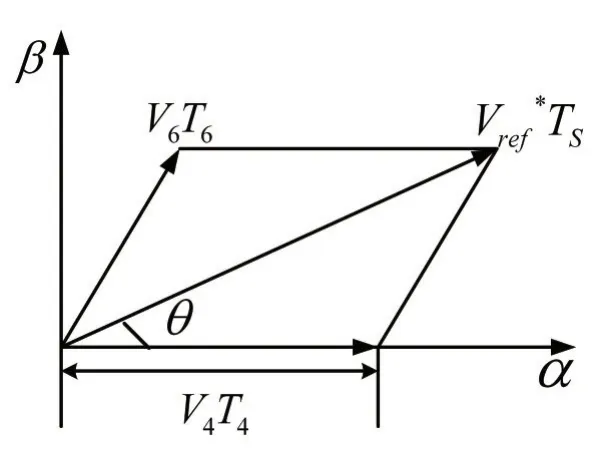
图3 参考电压的合成及分解图

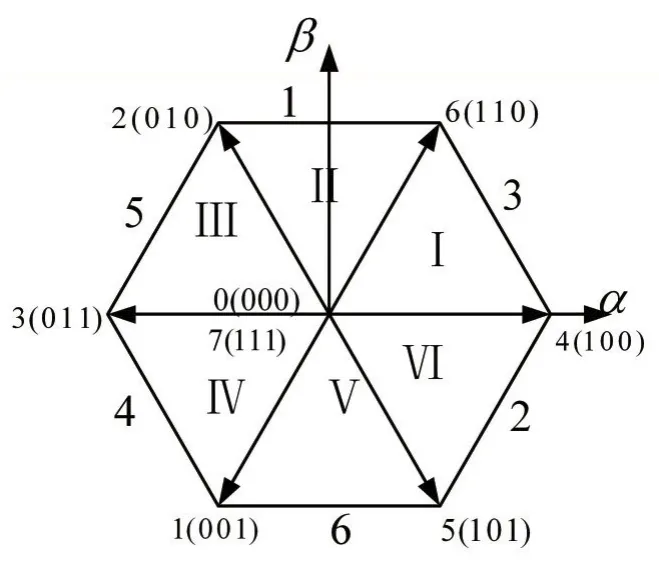
图4 参考电压矢量所在扇区的确定

2

2.1 参考电压矢量所处扇区NN的确定

在SVPWM中，首先是确定由Vα及Vβ所决定的空间电压矢量所处扇区，由前述分析可知，SVPWM优化开关调制模式下，参考矢量的合成与分解和传统空间矢量完全一样。所以参考矢量所在扇区的判断，可采用一样的方法，传统的确定方法是：利用Vα和Vβ求出电压矢量幅值，再根据Vα和Vβ的正负进行确定，但该方法因含有非线性函数，计算复杂度高。因此本文提出一种简单有效的确定方法[10]。

其先定义如下三个变量：

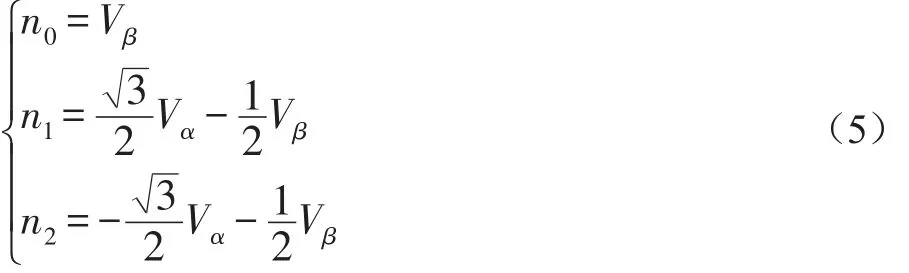
并定义：如果 n0＞0，则有 H=1，反之 H=0；如果n1＞0 ，则有 I=1，反之 I=0；如果 n2＞0 ，则有 J=1，反之J=0。

由H，I，J可形成八种组合，而由PWM原理可知H，I，J不能同时取1或同时取0，因此实际只有六种组合，且 H，I，J的取值与对扇区一一对应，故可由 H，I，J的不同组合来确定其所在扇区[11]。

为区别H，I，J的六种不同状态，设：

由上式可知，S可取整数值1至6，分别与六个扇区相对应，图4给出了利用式（6）确定的取值与实际扇区一一对应关系，图中棱形区域内的I至VI表示实际扇区号，而棱形区域外的1至6代表由式（6）求出的数值。

2.2 计算相邻四电压空间矢量的作用时间

完成参考电压矢量Vref*所处扇区判断后，要求计算出与Vref*相邻的四个电压矢量的作用时间。在传统电压空间矢量脉宽调制中，需要采用三角函数和空间角度，因此实现时大量数据需要计算并存储[12]。为此本文通过利用Vα和Vβ，来简化计算。

以图3中扇区I的矢量关系为例，令Vd、Ts分别为逆变器主电路的直流母线电压和采样周期，T4、T6分别为矢量V4、V6的作用时间，并通过下式求解V2、V5的作用时间T02：

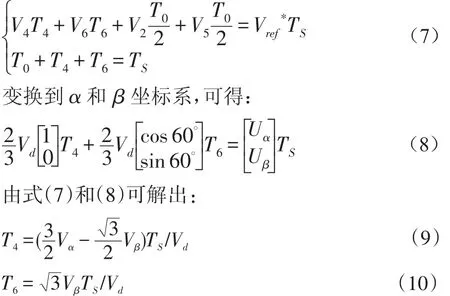
因V5和V2方向相反，且作用时间相等，故V5和V2的综合作用等同于零矢量，所以我们关注的是与参考电压相邻的V4、V6的作用时间T4、T6，当Vref*位于其他扇区中时，同理可求得各矢量作用时间，设与参考电压相邻的两电压矢量作用时间为Tu、Tv。解各方程后结果如表1所示。

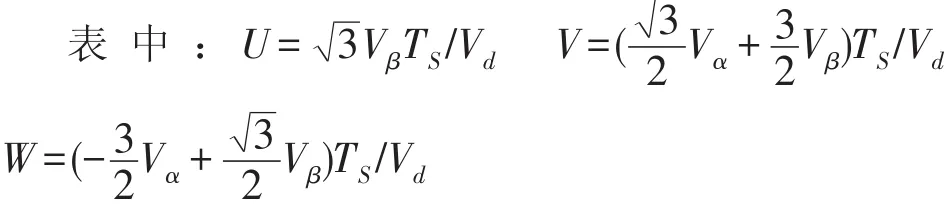
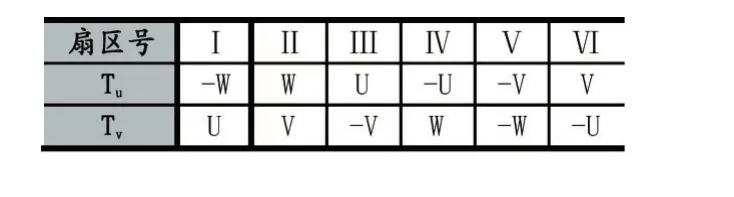
表1 Tu和Tv取值表

2.3 计算H,I,JH,I,J的开关时间Th、Ti、Tj

本文以第I扇区为例（如图5所示），利用输出SVPWM波形来计算Th、Ti、Tj。图5中给出了三相输出电压波形、三角载波及第I扇区的电压空间矢量序列[13]，Th、Ti、Tj表示与三角波比较后，用于产生SVPWMPWM波形的比较值，假设三角载波周期和幅值相等，并利用式（12）计算比较值：

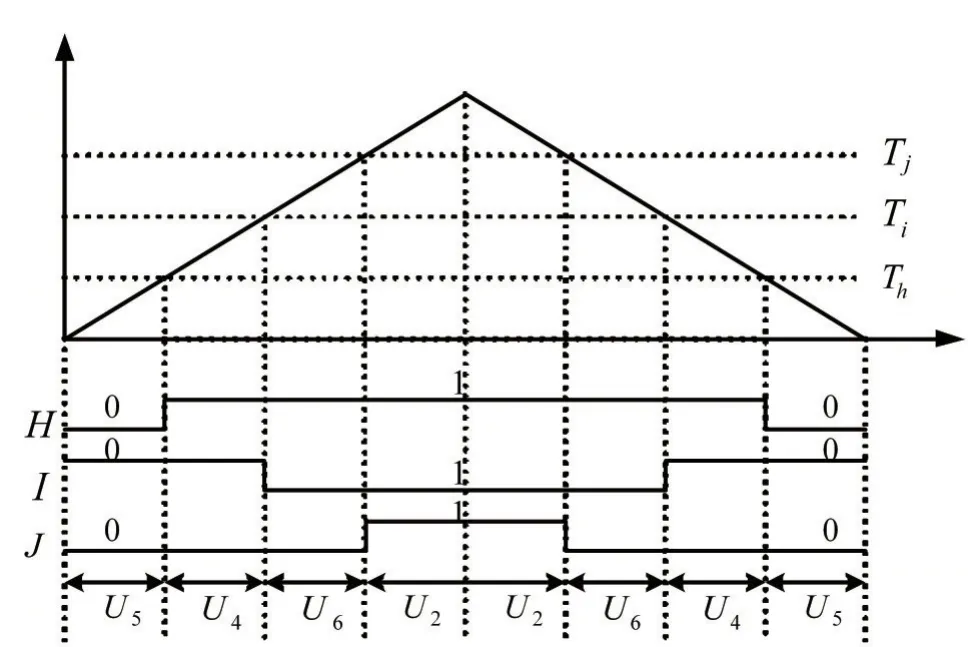
图5 扇区I内的SVPWM波形示意图

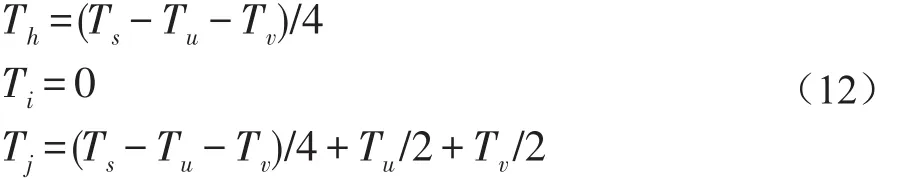
上式中，两个非零矢量的作用时间分别用Tu、Tv表示，不同扇区中对应不同矢量的作用时间Tu、Tv，但不管在任何一个扇区，最先作用的非零矢量时间均对应Tu（例如在扇区I中T4对应Tu），另一个非零矢量的作用时间对应Tv（例如在扇区I中T6对应Tv）。在一个载波周期中，根据各扇区PWM波形来确定三个比较值具体分配给哪一相，如占空比最大的相由Th分配，占空比最小的相由Tj分配。

由前述分析，并根据在连续开关调制模式中各扇区的PWM波形，可得不同的扇区内H，I，J三相对应的开关时间Th、Ti、Tj可根据表2进行赋值：

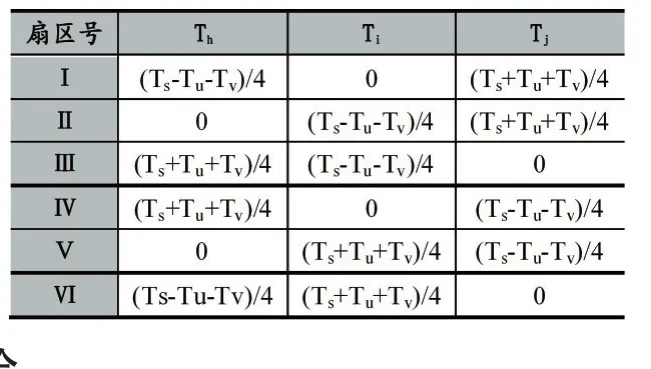
表2 切换点Th、Ti、Tj的取值表

3 实验

为验证所提方案的有效性，利用一台异步电动机为研究对象，进行了相关的实验论证。实验中异步电动机的参数设置如下：异步电动机采用星型接法，PWM开关频率设为10KHz，母线电压Vdc=310V。图6和图7分别为采用传统SVPWM控制方式和采用优化SVPWM控制方式的电机共模电压的电机共模电压VCM。

比较图6和图7，可以看出，优化SVPWM控制方式有效降低了共模电压。

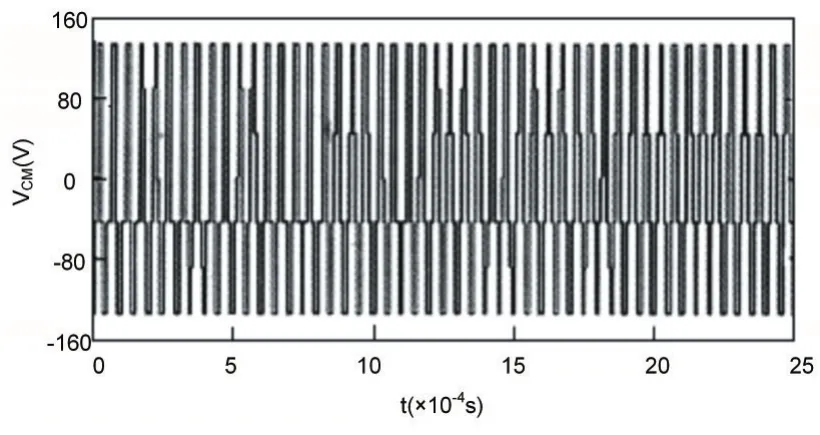
图6 采用传统SVPWM控制方式的共模电压

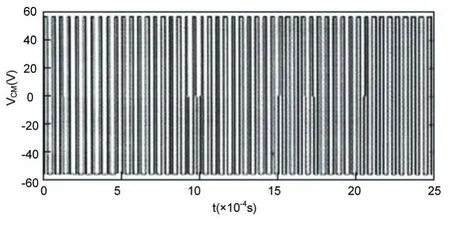
图7 采用优化SVPWM控制方式的共模电压

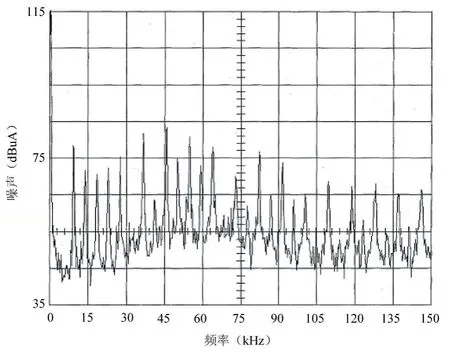
图8 实验的传统SVPWM共模EMI

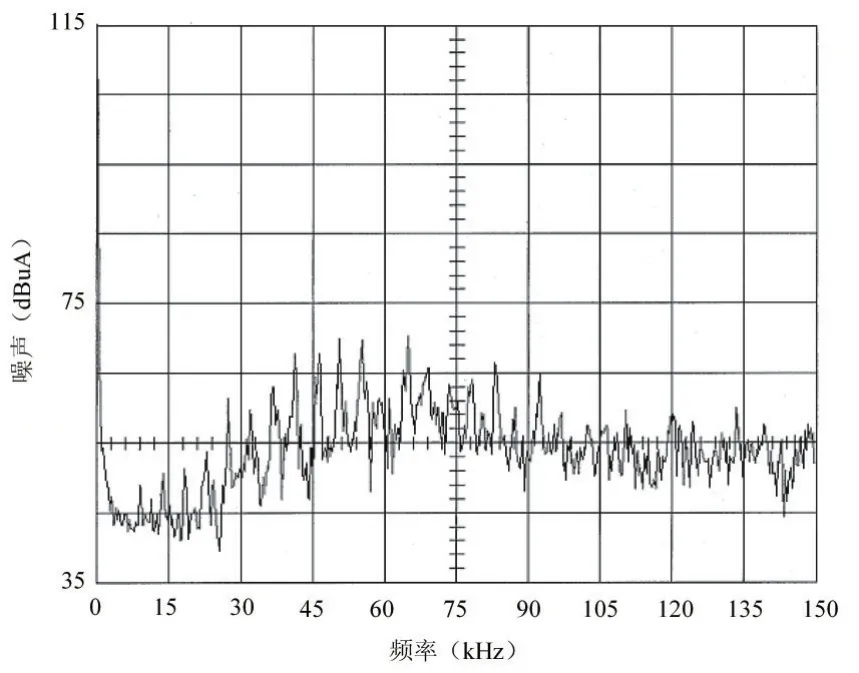
图9 实验的优化SVPWM共模EMI

另外，从频域考虑，对共模电流利用高频电流夹钳在两种调制模式下（传统SVPWM和优化SVPWM）在同样的条件下 f0=20Hz,fs=5kHz进行了实验。测量的频谱如图8和9所示。对比图8和图9可以看出，采用优化的SVPWM调制方法时系统的共模干扰比采用传统的SVPWM调制方法时大大减小，最高达到20dB以上。

4 结语

本文在对PWM控制技术发展现状进行分析的基础上，介绍了三相逆变器的电磁干扰和共模电压，提出了旨在降低EMI的SVPWM控制策略的优化方案，分析了其控制原理，得出了SVPWM控制策略优化方案。并分别采用传统SVPWM控制方式和优化SVPWM控制方式控制一台异步电动机，进行了实验研究。实验结果表明，优化SVPWM控制方式在保证逆变器输出电压的同时，有效地减小了共模电压。另外，从频域考虑，在同样的条件下对共模电流在两种调制模式下（传统SVPWM和优化SVPWM）进行了实验。通过对比两种调制模式下所测量到的EMI频谱说明，采用优化的SVPWM调制方法时系统的共模干扰比采用传统的SVPWM调制方法时大大减小，最高达到20dB以上。

[1]陈国呈.PWM变频调速及软开关电力变换技术[M].北京：机械工业出版社，2001：175-180．

[2]张蓉.数字控制SPWM逆变器研究[D]．南京：南京航空航天大学，2006.

[3]杜荣权，陈乐柱，穆瑜.PWM型动态无功补偿技术的研究[J].电源学报，2015，13（4）：53-57.

[4]陶兴华，李永东，孙敏.一种H桥级联型PWM整流器的直流母线电压平衡控制新方法[J].电工技术学报，2011，26（8）：85-90.

[5]戴珂，徐晨，丁玉峰，康勇.载波轮换调制在级联H桥型STATCOM中的应用[J].中国电机工程学报，2013，12（33）：99～106

[6]李宁，王跃，雷万钧，王兆安.三电平NPC变流器SVPWM策略与SPWM策略的等效关系研究[J].270电网技术，2014，38（05）：1283-08.

[7]王水平，周培志，张耀进.PWM控制与驱动器使用指南及应用电路[M].西安：西安电子工业出版社，2005：1-25．

[8]于泽琦，王凤琴，李祖贺等.一种改进的数字PWM发生器非线性误差预校正方法[J].计算机应用研究，2017，2（34）：433-437．

[9]刘云，贾洪平，张鹏等.基于SVPWM的无刷直流电机矢量控制系统研究[J].机电工程，2014，31（9）：1177-1181.

[10]武健，刘瑜超，徐殿国.基于模块多电平变换器的并联有源滤波器控制策略研究[J].电工技术学报,2013,28（12）：52-59.

[11]吴洪洋，何湘宁.多电平载波PWM法与SVPWM法之间的本质联系及其应用[J].中国电机工程学报.2002，22（5）：10-15.

[12]徐鹏，施火泉，刘会超.容错逆变器的三相四开关矢量控制策略[J].江南大学学报，2015，14（5）：601-605.

[13]张伽伟.嵌入式系统在通信装备状态监测中的应用[D].武汉：海军工程大学，2012.

An Improved Scheme of the SVPWM Control Strategy

HUA Guo-xin
（Zhejiang Guangsha Construction Vocational&Technical College,Dongyang 322100）

On the basis of analyzing the developing history and present status of soft-switching technique,analyzes the operating principle and char⁃acteristic of SVPWM in detail,proposes the optimization scheme of the SVPWM control strategy that aiming at reducing EMI,analyzes and tests the soft-switching inverter prototypes are simulation,and the results show the correctness of the analysis,and the rationality of param⁃eter design.

1007-1423（2017）23-0027-05

10.3969/j.issn.1007-1423.2017.23.006

华国新（1965-），男，浙江东阳人，高级工程师，本科，研究方向为机电一体化技术

2017-04-27

2017-07-30

Soft-Switching;Three-Phase Inverter;SVPWM