基于提升小波变换与EEMD的神经网络齿轮故障诊断方法*

宋萌萌，肖顺根,2，陈肇祥

(1.宁德师范学院 物理与电气工程系，福建 宁德 352100； 2.上海大学 机电工程与自动化学院，上海 200072)

基于提升小波变换与EEMD的神经网络齿轮故障诊断方法*

宋萌萌1，肖顺根1,2，陈肇祥1

(1.宁德师范学院 物理与电气工程系，福建 宁德 352100； 2.上海大学 机电工程与自动化学院，上海 200072)

针对单一的信号处理诊断方法难以实现齿轮故障准确诊断的局限性，文章将提升小波变换、集成经验模态分解(ensemble empirical mode decomposition，EEMD)与相关系数相结合，提出一种新的信号消噪方法，并在此方法的基础上，分别利用BP、Elman和RBF神经网络完成了齿轮故障诊断。首先采用提升小波变换对故障信号进行初步消噪，然后对其作EEMD分解，得到一组固有模态函数(intrinsic mode function, IMF)分量；然后计算各分量的相关系数，剔除相关性较小的伪分量后进行重构，完成二次消噪；最后计算剩余分量的能量特征，并将其作为神经网络的输入向量，进而完成齿轮断齿、裂纹和磨损状况下的故障诊断。仿真分析和应用实例表明：基于提升小波变换与EEMD分解并结合相关系数筛选的消噪方法，比仅用提升小波方法消噪的效果更好。三种神经网络均成功辨别出了齿轮的故障类型，但不同方法各有优劣之处；就诊断效率和准确性而言，BP神经网络的诊断效果最好。

提升小波变换；EEMD；相关系数法则；神经网络

0 引言

齿轮是机械设备中最重要的连接和传动部件，及时发现齿轮在传动过程中的故障，能经济合理地安排设备的维护与维修时间，避免发生事故[1]。目前的齿轮故障诊断方法多建立于采集振动信号的基础上，尚无较为系统的诊断方法，因此本文对齿轮故障诊断方法的探索具有一定的应用价值。

早期的傅里叶变换只给出了信号在时频域的统计平均结果，无法同时兼顾信号在时频域中的全貌和局部化信息[2]。小波分析的多尺度特性能较好地表征局部信息、辨别信号突变，但其本质上是窗口可调的傅里叶变换，小波基函数有限的长度导致对信号作小波变换时会产生能量泄露[3-4]。同时，当确定了小波基函数及其分解层数时，每个节点只反映固定频段的分析结果，缺乏自适应性[5]。Huang.N.E.等提出的EMD可依据信号本身的时变特性进行自适应分解，相比于小波变换，它对故障信息更敏感、网络识别率更好[6]，但EMD在分解过程中易出现模态混叠、端点效应，基于此，Huang又提出了改进算法EEMD。

故障诊断的实质是模式识别问题。由于齿轮故障信号是非线性非平稳的，而神经网络具有很强的非线性映射与容错能力，特别适合非线性的模式识别与分类[7]，故将其引入故障诊断之中。本文采用提升小波变换对故障信号进行初步消噪，然后对其EEMD分解得到一组IMF分量，剔除相关性较小的伪分量后进行重构，完成消噪；最后计算剩余各分量的能量百分比，作为神经网络的输入。仿真分析充分验证了本文提出的消噪方法具有良好的消噪效果，应用实例证明了三种神经网络均能成功辨别齿轮的故障类型。

1 诊断方案原理简介

1.1 EEMD原理

EEMD是EMD的改进方法，它基于数据本身分解、不需要事先设定基函数，这使得各分量的瞬时频率具有物理意义，同时也避免了分量间的模态混叠。所谓的模态混叠，是由于极值点分布不均或极值点数目不够，在对信号作包络时产生拟合误差所引起的。EEMD利用高斯白噪声具有频率均匀分布的特性，使加噪信号的分解尺度均匀分布，抑制了脉冲干扰；同时，改变了信号极值点的特性，使信号在不同尺度上具有连续性[8]。

EEMD分解过程步骤如下[9]：

步骤1：给输入信号x(t)添加N次均值为零、标准差为常数的高斯白噪声ωi(t)，构建初始信号xi(t)，即：

xi(t)=x(t)+ωi(t)

(1)

其中，ωi(t)的大小取决于白噪声标准差和初始信号标准差的比值Nstd，i=1～N，Nstd通常设为0.2。

步骤2：对初始信号xi(t)进行EMD分解，获得l个固有模态函数IMF分量及1个余项ri(t)。

(2)

其中，yij(t)是第i次加入高斯白噪声后经EMD分解产生的第j个IMF分量。

步骤3：求各个IMF分量yij(t)的均值，获得IMF分量yj(t)和余项r(t)，这一步骤能降低甚至消除所加入的ωi(t)对IMF的影响。

(3)

(4)

其中，yj(t)是对信号x(t)作EEMD分解后得到的第j个IMF分量。

因此，被EEMD分解的信号x(t)可由l个yj(t)和1个r(t)构成，如式(5)所示。

(5)

1.2 提升小波变换

提升小波变换(lifting wavelet transform，LWT)与传统小波的区别在于构造小波基函数时不依赖傅立叶变换，不再通过某个函数平移或伸缩而产生，直接在时域中实现信号在不同频带上的分离[10]。LWT采用插值法来拟合信号高频分量，构造尺度函数以获得低频分量，将提升变换分三个步骤：分解、预测和更新。

步骤1：分解。根据输入信号si的奇偶性将其分为2个低分辨率子集si-1和di-1，di-1称为小波子集。

si-1,k=si,2k

(6)

di-1,k=di,2k+1

(7)

其中，k=0,1,…，2i-1-1。

步骤2：预测。用偶数序列si-1去预测奇数序列di-1，通过对相邻两个偶数si,2k和si,2k+2作线性平均来预测奇数位置si,2k+1的di-1,k，奇数序列与预测值的差作为细节系数构造小波函数。

di-1,k=si,2k+1-(si,2k+si,2k+2)/2

(8)

步骤3：更新。更新的目的是寻找一个子集si-1以保持原信号的某些标量特性不变(如均值)，在子集si-1中继续保持某些全局特性。

1.3 相关系数准则

由于信号包含丰富的噪声，分解得到的信号中只有一部分分量含有有效信息，因此需要剔除相关性较小的伪分量，实现消噪。关于相关系数阈值的设置方法目前尚无统一的标准，依经验与具体的数据情况而定.相关系数公式如式(9)所示。

(9)

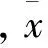
1.4 神经网络原理

为了对比不同网络的诊断效果，本文分别采用BP、RBF和Elman三种网络进行诊断。网络由输入层、隐含层和输出层构成。输入层接收的输入信号经由各输入单元传递给对应的隐含层单元；隐含层是神经网络的内部处理中枢，网络的模式变换(如模式分类)主要体现于隐含层单元的处理；输出层产生网络的输出模式[11]。

BP网络是一个前向型网络，训练过程中误差反向传播，通过隐含层向输入层逐层分摊误差、调整权值连接强度，交替重复训练直至收敛到一个固定阈值。

RBF网络的输入层由信号源节点组成；隐含层采用径向基函数，不需要权连接即可将输入向量映射到隐含层；输出层是线性层，完成对隐含层空间模式的分类。网络的输出是隐单元输出的线性加权和，网络的权可由线性方程直接解出，避免了陷入局部极小问题。

Elman网络具有从隐含层输出到隐含层输入的反馈，这种反馈结构使得其被训练后不仅能够识别和产生空域模式，还能够识别和产生时域模式。它的第一层有一个反馈节点，该节点的延迟量储存了上一时刻的值，并将其运用于本时刻计算。所以即使两个网络的权值阈值相同，对于同样的输入，反馈状态不同，同一时刻的输出也不尽相同。

2 信号采集与能量特征提取

2.1 故障信号采集

实验装置搭建涉及到的硬件主要有QPZZ-II旋转机械振动分析及故障诊断试验平台系统、信号调理仪一台、数据采集器两台、加速度传感器若干，实验台示意图如图1所示。该实验平台的小齿轮为主动轮，与电机轴相连；大齿轮为从动轮，通过联轴器与磁粉制动器相连。在主动轴上贴一圈黑胶布(留2mm左右的狭缝反光)，采用红外测速器测量轴的转速。小齿轮的齿数为55，大齿轮的齿数为75，在齿轮箱外侧大齿轮处的水平与垂直两个方向各安装一个加速度传感器，两个传感器的标定值分别为102mV/g与99mV/g，测点布置如图2所示。

图1 实验平台示意图

分别采集正常信号及裂纹、断齿和磨损三种典型故障信号，采用双通道数据采集，其中故障数据采用通道一的数据。为保证采集到足够的数据样本，采样频率必须是分析频率的2.56倍以上。

图2 传感器测试点布置

2.2 故障信号的能量特征提取

系统受到激励时，产生的振动信号将使某些分量的幅值或频率发生调制，引起信号的能量变化。因此，各分量的能量变化反映了齿轮的故障情况，将各分量能量归一化后作为网络的输入。

提取能量特征的步骤如下：

(1)用提升小波变换和EEMD相结合方法进行消噪，然后采用相关系数准则筛选出含有主要故障信息的前k个IMF分量；

(2)求各分量能量Ei，如式(10)所示；

(10)

(3)构造能量特征向量T：考虑到各分量的能量值差别较大，不利于网络的收敛，故先将能量归一化。归一化的方法有好多种，其中求各分量能量占总能量的百分比是比较典型的一种，能量特征如式(12)所示。

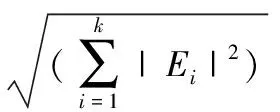
(11)

T=[E1/E,E2/E,…Ek/E]

(12)

3 信号消噪仿真

(1)为了模拟含噪信号，采用MATLAB中自带的leleccum信号，添加幅值为100的矩形方波信号作为冲击成分，构成原始信号x(t)。用randn函数添加幅值为15的标准噪声，两种信号的采样点均数设为1000，构成含噪信号x1(t)。原始信号x(t)如图3所示。

图3 原始信号x(t)

(2)采用提升小波变换法和本文提出的新方法分别对含噪信号进行消噪。本文提出的新消噪方法是在提升小波消噪基础上，再采用EEMD对信号进行分解，将EEMD算法中的Nstd设为0.2，添加1000次高斯白噪声，得到9个IMF分量和1个余量，如图4所示。最后，再利用相关系数准则进行筛选有效IMF分量，筛选过程如下的步骤(3)和(4)所示。

(3)计算各分量的相关系数，如表1所示。

(4)根据经验值，设置相关系数阈值μ=0.2，IMF1、IMF2、RES的相关系数都小于0.2，因此将其剔除。重构剩余分量，得到筛选后的有效信号，如图5d所示。结果表明，采用提升小波消噪方法效果(如图5c所示)的信噪比低于新方法，因此，新方法的消噪效果更好。

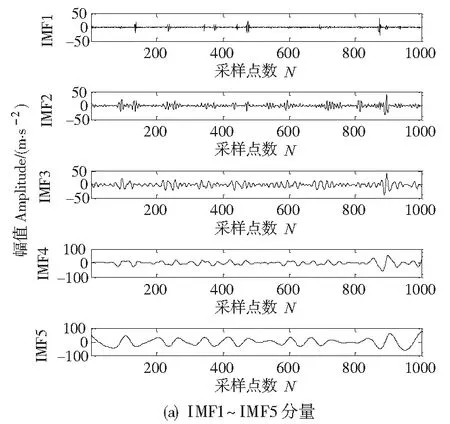
图4 各IMF分量示意图

表1 各分量相关系数

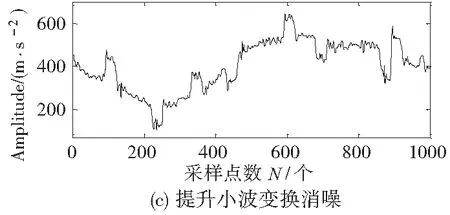
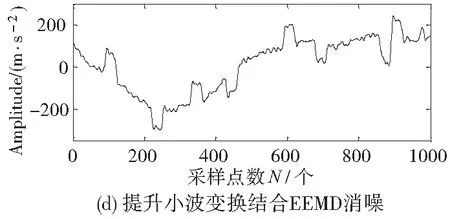
图5 信号消噪效果

4 应用实例

为了对比不同网络的诊断效果，找到最佳的诊断系统，本文采用了RBF、BP和Elman三种神经网络，诊断流程图(以BP网络为例)如图6所示。

图6 BP网络诊断流程图

具体诊断步骤如下(因篇幅原因，以断齿为例)：

(1)对断齿信号作提升小波变换消噪，如图7所示。

图7 断齿信号初步消噪

(2)对初步消噪信号作EEMD分解，分解示意图如图8所示。

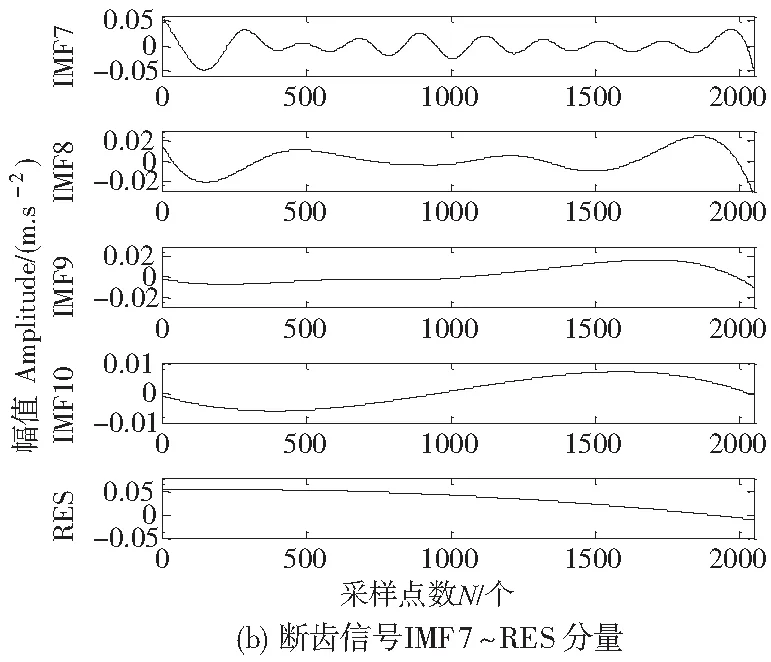
图8 断齿信号IMF分量

(3)计算各分量的相关系数，如表2所示。

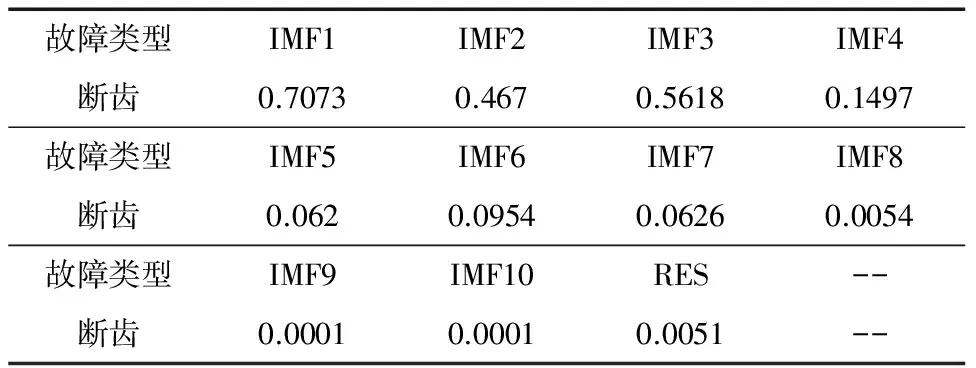
表2 各分量的相关系数

(4)设定阈值μ为0.1，IMF4之后的相关系数已小于0.1，故选择大小位于前4的分量计算其能量特征，作为网络的输入。信号的能量谱如图9所示。

图9 信号故障能量谱分布

(5)设置网络的参数。网络参数设定可参考文献[12]。输入神经元数为4，对应四个能量特征；输出神经元数也为4，分别对应四种故障模式编码：断齿(1,0,0,0)、裂纹(0,1,0,0)、磨损(0,0,1,0)、正常(0,0,0,1)。关于隐含层数目的确定方法，目前应用较多有以下两种：

2)实验法。当隐含层数目设在输入层数目和输出层数目之间或附近时，网络的收敛速度较快。

通过仿真实验，综合上述两种方法，确定隐含层数目为4。BP网络和Elman网络输出层和隐含层的传递函数分别设为purelin和logsig，最小均方误差设为10-8，训练步长为1000；RBF网络的输出层和隐含层的传递函数分别设为purelin和radbas，最小均方误差仍设为10-8，扩展系数为1。

为了检验三种神经网络对齿轮故障诊断的效果，均以齿轮故障能量信号特征作为神经网络的输入，齿轮的故障类型为网络输出。以60组齿轮故障能量信号特征量进行网络训练，如表3所示(因篇幅关系，仅列出3组)。

用20组样本数据分别对三种神经网络进行故障诊断测试，其中BP神经网络成功诊断18次，RBF神经网络成功诊断16次，Elman神经网络成功诊断18次。表4和表5分别为三种神经网络在诊断成功情况下的实际输出平均值和诊断误差的平均值。

表3 故障信号能量特征

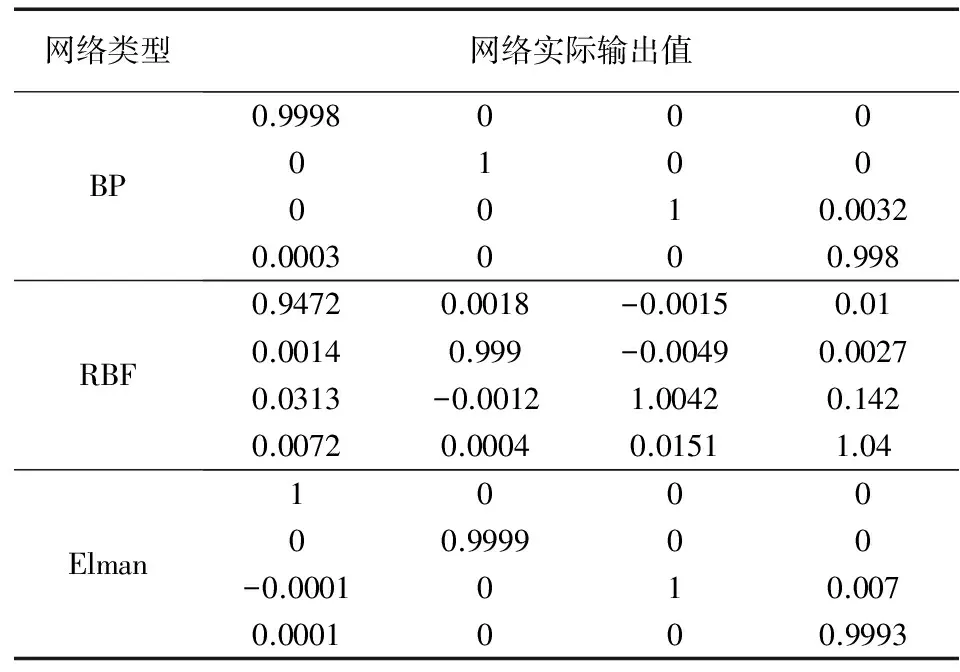
表4 三种神经网络实际输出平均值

上述三种网络所用的训练步长及诊断时间如表6所示，网络训练步长示意图如图10、图11所示。

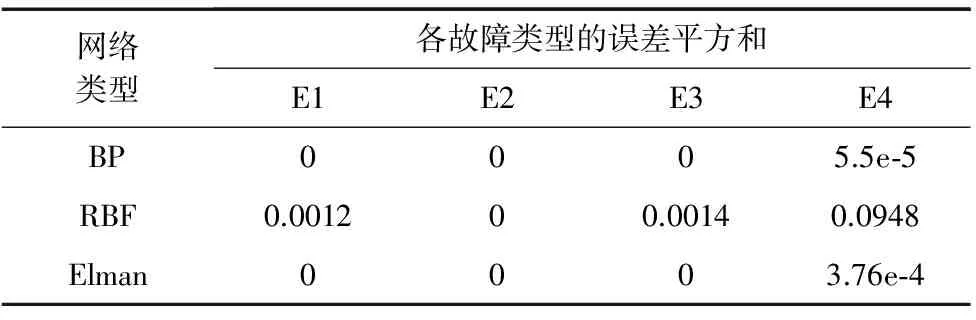
表5 三种神经网络诊断误差平均值

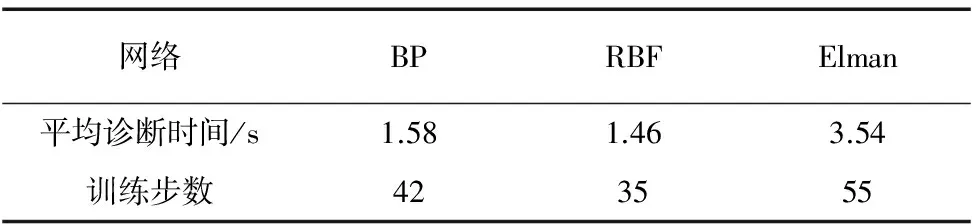
表6 三种网络诊断时间与训练步长的平均值

图10 BP网络达到最小均方误差训练步数

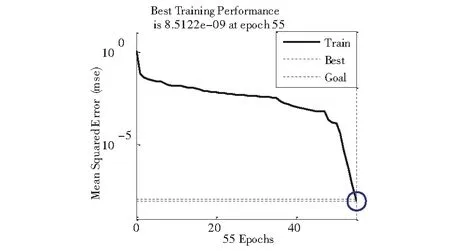
图11 Elman网络达到最小均方误差训练步数

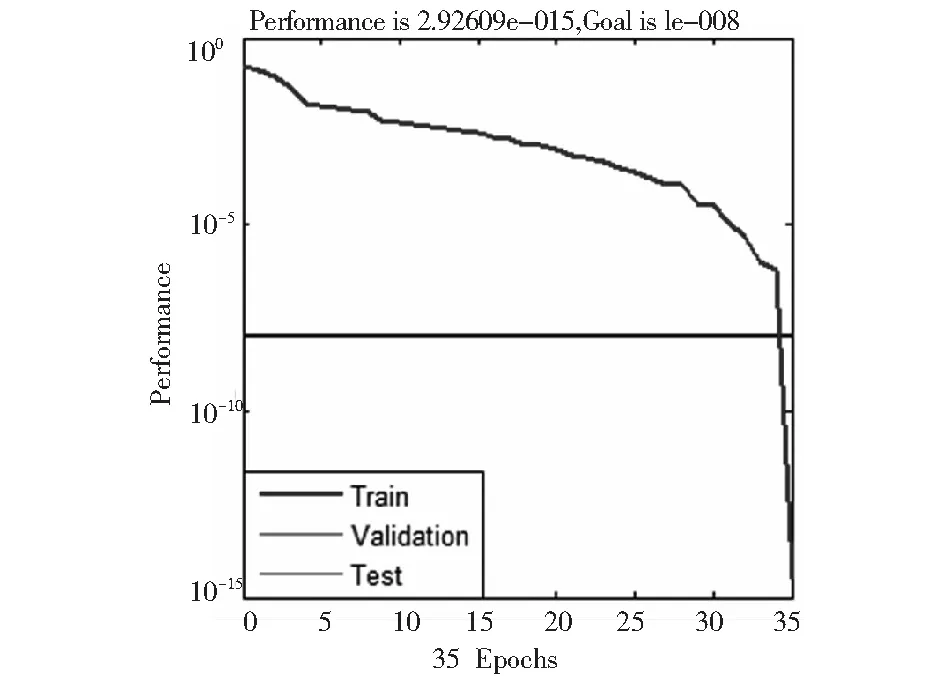
图12 RBF网络达到最小均方误差训练步数

结果表明：RBF网络的收敛速度最快但诊断精度很大程度上依赖于测试样本的好坏，诊断结果波动较大，诊断精度最低；Elman网络的诊断时间较长,诊断精度较好；BP网络的诊断精度与Elman网络相近，且略胜于Elman网络，就诊断精度与诊断效率综合而言，BP网络的诊断效果最佳。

5 结论

通过以上的仿真及实例分析，得出如下结论：

(1)在信号消噪仿真过程中，采用小波包消噪会致使消噪力度过大，导致幅值较小的有效信号也被消除，对于幅值较小的信号尤其如此。而本文提出的基于提升小波变换与EEMD分解并结合相关系数筛选的消噪方法，具有很好的消噪效果。

(2)BP网络、RBF网络和Elman网络均能成功辨识出故障类型，其中RBF网络过于依赖测试样本数据好坏，诊断误差最大，但诊断效率最高；

(3)Elman网络和BP网络的诊断误差相近，但Elman网络诊断效率不足BP网络诊断效率的一半。综合而言，BP神经网络更适合用于齿轮故障的诊断系统中，为后期进一步开展优化神经网络故障诊断系统奠定较好基础。

[1] 潘巍巍, 宋彦萍, 于达仁. 齿轮裂纹程度识别的有序分类算法[J]. 哈尔滨工业大学学报, 2016, 48(7):156-162.

[2] Shao Renping, Hu Wentao, Huan Xinna, et al.Multi-damage feature extraction and diagnosis of a gear system based on higher order cumulant and empirical mode decomposition[J]. JOURNAL OF VIBRATION AND CONTROL, 2015, 21(4):736-754.

[3] 于德介,程军圣,杨宇. Hilbert-Huang变换在齿轮故障诊断中的应用[J].机械工程学报,2005,41(6):102-106.

[4] 杨晋溥, 崔超, 冯辅周,等. 基于小波相关—包络排列熵的齿轮故障特征提取[J].机械设计与制造, 2015(11):268-272.

[5] Huang N E,Shen Z, Long S R.The empirical mode decomposition and the Hilbert spectrum for nolinear and non-stationary time series analysis[J].In:Proc.R.Soc.Lond.A,1998,454:903-995.

[6] 肖成勇, 石博强, 冯志鹏. 基于EEMD和进化支持向量机的齿轮混合智能诊断方法研究[J]. 机械科学与技术, 2015, 34(1):86-89.

[7] 陈换过,江金寿,李剑敏,等. 基于提升小波包和神经网络的结构损伤检测[J]. 振动、测试与诊断,2013,33(1):116-121.

[8] 吕建新,吴虎胜，田杰. EEMD的非平稳信号降噪及其故障诊断应用[J].计算机工程与应用，2011,47(28) :223-227.

[9] 肖顺根,宋萌萌,孔庆光,等. 基于EEMD降噪与非抽样提升小波包的滚动轴承故障诊断新方法[J].延边大学学报,2015,41(1):57-63.

[10] 曹满亮，潘宏侠.基于第二代小波及PNN的自动机智能故障诊断[J]. 机械设计与研究, 2015, 31(3):22-26.

[11] 张德丰. MATLAB神经网络应用设计[M]. 2版.北京: 机械工业出版社,2011.

[12] Li, Qing. Fault Diagnosis of Some Equipment Based on BP Neural Network [J]. Applied Mechanics and Materials, 2014(644-650):1193-1196.

[13] 沈花玉,王兆霞,高成耀,等. BP神经网络隐含层单元数的确定[J]. 天津理工大学学报,2008,24(5):13-15.

(编辑李秀敏)

NeuralNetworkFaultDiagnosisMethodofGearBasedonEEMDandLiftingWaveletTransform

SONG Meng-meng1, XIAO Shun-gen1,2, CHEN Zhao-xiang1

(1.Department of Physics and Electrical Engineering, Ningde Normal University, Ningde Fujian 352100, China;2.School of Mechatronical Engineering and Automation, Shanghai University, Shanghai 200072,China)

There are limitations which are difficult to achieve accurate diagnosis of gear fault using a single signal processing diagnosis method, this paper presents a new signal denoise method of fault diagnosis which is based on ensemble empirical mode decomposition and lifting wavelet transform and correlation coefficient.And on the basis of this method, the gear fault diagnosis is completed by using BP, Elman and RBF neural networks.The lifting wavelet transform is used for preliminary denoise of the fault signal, and then get a set of intrinsic mode function components by using EEMD. Calculated the correlation coefficients between the IMF components and the initial signal, then reconstruct the signal by remove the spurious components with a small correlation to achieve the purpose of further denoise. Calculating the energy characteristic of the remaining components, and set them as the input vector of the neural networks to complete the fault diagnosis of the gear tooth broken, the crack and the wear condition.Simulation analysis and application examples show that this denoise method has a very better effect than the lifting wavelet transform, which is based on the lifting wavelet transform and EEMD and the correlation coefficient. Three kinds of neural networks have successfully identified the fault type of the gear, but different methods have their own advantages and disadvantages.In terms of diagnostic efficiency and accuracy,BP neural network has the best diagnostic effect.

lifting wavelet transform; EEMD; correlation coefficient rule; neural network

TH165+.3;TG506

：A

1001-2265(2017)09-0093-06

10.13462/j.cnki.mmtamt.2017.09.024

2016-11-20

福建省自然科学基金项目(2015J01643)；福建中青年教师教育科研项目(JA15545)；宁德市科技计划项目(20150034)；福建省高校杰出青年科研人才培育计划资助(闽教科〔2015〕54号)

宋萌萌(1982—)，女，河北保定人，宁德师范学院讲师，硕士，研究方向为人工智能和机械设备故障诊断，(E-mail)544824964 @qq.com。