不定方程整数解的讨论

尚 旭,李龙刚

(1.浙江师范大学数学系,浙江金华321004;2.济邦教育科技,陕西西安710000)

不定方程整数解的讨论

尚 旭1,李龙刚2

(1.浙江师范大学数学系,浙江金华321004;2.济邦教育科技,陕西西安710000)

在高斯整数环中,利用代数数论的方法,研究几个不定方程的整数解,推进了不定方程的研究.

高斯整环;不定方程;整数解;代数数论

设A、B∈N,A无平方因子,关于不定方程

Ax2＋B＝Cyn,(x,y,n∈N,n≥2)(1)解的问题是数论中的一个重要问题.近些年,研究者用代数数论的方法研究了许多形式的不定方程,如:当A＝1,B＝1,C＝1时Ledesgue证明了无整数解;Nagell证明了当A＝2,B＝1,C＝1,n＝5时,仅有整数解(x,y)＝(±11,3);孙树东证明了A＝1,B＝64,n＝13,C＝1时无整数解;杨全证明了A＝1,B＝16,n＝9,C＝1时无整数解;李中恢,张四保证明了A＝1,B＝16,n＝11,C＝1时无整数解;张四保,吕明富证明了A＝1,B＝64,n＝13,C＝4时无整数解.基于此,研究当A＝1,B＝256,C＝4,n＝3,5,7时方程x2＋256＝4yn的整数解问题.[1－6]

1 定理及其证明

引理17[]设M是惟一分解整数环,正整数k≥2,以及α,β∈Z,(α,β)＝1αβ＝τk,τ∈M,则有α＝ε1μk,β＝ε2νk,μ,ν∈M,其中ε1,ε2是M中的单位元素,并且ε1ε2＝εk,ε为单位元素.

引理28[]不定方程x2＋64＝y3当x≡1 (mod 2)时,无整数解.

引理39[]不定方程x2＋64＝y5无整数解.

引理410[]不定方程x2＋64＝y7仅有整数解(x,y)＝(±8,2).

定理1:不定方程x2＋256＝4y3x,y∈Z (2)

仅有整数解(x,y)＝(0,4).

证明:分两种情况说明

(1)当x≡1(mod2)时

则在Z i[]中,(2)可以等价为(x＋16i)(x－16i)＝4y3,x,y∈Z.

因为x≡1(mod2)时,有x＋16i≡1(mod2),所以η≠2.

产生矛盾,所以η＝1.

由此和引理1得

x＋16i＝4(a＋bi)3,x,a,b∈Z

因此得

由(4)式得b＝±1,±2,±4

当b＝1时,由(4)式得

16＝4(3a2－1),

即 5＝3a2.(5)

因为a∈Z,所以找不到a使(5)式成立.

所以b＝1时不成立.

当b＝－1时,由(4)式得

16＝－4(3a2－1),

－3＝3a2.(6)

显然(6)不成立.所以b＝－1时不成立.

似上述证明,可知当b＝±2,±4时不成立.

则当x≡1(mod2)时,不定方程(2)无整数解.

(2)当x≡0(mod2)时

易知x为偶数,可设x＝2x1,x1∈Z代入(2)得x12＋64＝y3(7)

接下来,讨论x2＋64＝y3的整数解情况.

也分两种情况,当x≡1(mod2),引理2已经证明无整数解.

当x≡0(mod2)时

易知x为偶数,y也是偶数,则设x＝2x1,y＝2y1x1∈Z,y1∈Z代入x2＋64＝y3中得

x12＋16＝2y13

易知x1为偶数,设x1＝2x2,x2∈Z,代入上式得:2x22＋8＝y13

易知y1为偶数,设y1＝2y2,y2∈Z,代入上式得:x22＋4＝4y23

易知x2为偶数,设x2＝2x3,x3∈Z,代入上式得:x32＋1＝y23

易求得上式只有整数解(x3,y2)＝(0,1).

从而我们可知x12＋64＝y3仅有整数解(x1,y)＝(0,4).

综上,可知不定方程(2)仅有整数解(x,y)＝(0,4).

定理2:

不定方程 x2＋256＝4y5x,y∈Z(8)

无整数解.

证明:分两种情况说明

(1)当x≡1(mod2)时

则在Z i[]中,(8)可以等价为(x＋16i)(x－16i)＝4y5,x,y∈Z.

因为x≡1(mod2)时,有x＋16i≡1(mod2),所以η≠2.

产生矛盾,所以η＝1.

由此和引理1得

x＋16i＝4(a＋bi)5x,a,b∈Z

则在Z i[]中,(14)可以等价为(x＋16i)(x－16i)＝4y7,x,y∈Z.

因为x≡1(mod2)时,有x＋16i≡1(mod2),所以η≠2.

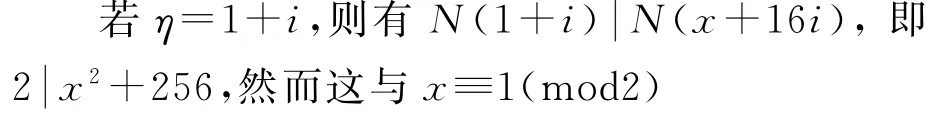
产生矛盾,所以η＝1.

由此和引理1得

x＋16i＝4(a＋bi)7x,a,b∈Z

因此得

x＝4(a5－10a3b2＋5ab4),(9)

16＝4b(5a4－10a2b2＋b4).(10)

由(10)式得b＝±1,±2,±4

当b＝1时,由(10)式得

16＝4(5a4－10a2＋1)

3＝5(a4－2a2)(11)

因为5不能整除3,所以(11)不成立.

所以b＝1不成立.

当b＝－1时,由(10)式得

16＝－4(5a4－10a2＋1)

－1＝a2(a2－2)(12)

(12)式要成立,则a2＝1,

代入(12)式a2(a2－2)＝－1成立.

将a2＝1,b＝－1代入(9)式,解得x＝±16,然而这与x≡1(mod2)矛盾,所以不成立.

所以b＝－1不成立.

似上述证明,可知当b＝±2,±4时不成立.

则当x≡1(mod2)时,不定方程(8)无整数解.

(2)当x≡0(mod2)时

易知x为偶数,可设x＝2x1,x1∈Z代入(12)得

x12＋64＝y5(13)

而对于(13)式的不定方程,引理3已证明无整数解.

综上,不定方程(8)无整数解.

定理3:不定方程

x2＋256＝4y7x,y∈Z(14)

仅整数解(±16,2).

证明:分两种情况说明

(1)当x≡1(mod2)时

因此得

x＝4(a7－21a5b2＋35a3b4－7ab6),(15)

16＝4b(7a6－35a4b2＋21a2b4－b6).(16)

由(16)式得b＝±1,±2,±4

当b＝1时,由(16)式得

5＝7(a6－5a4＋3a2)(17)

因为7不能整除5,所以不存在a∈Z满足(17)式.所以b＝1不成立.

当b＝－1时,由(16)式得

－3＝7(a6－5a4＋3a2)(18)

因为7不能整除－3,所以不存在a∈Z满足(18)式.

类似上述证明,可知当b＝±2,±4时不成立.

所以当x≡1(mod2)不定方程(14)无整数解.

(2)当x≡0(mod2)时

易知x为偶数,可设x＝2x1,x1∈Z代入(14)得x12＋64＝y7

(19)

而对于形如(19)式的不定方程,引理4已证明此方程仅有整数解(±8,2).

继而可求得(x,y)＝(±16,2)

综上,可知不定方程(14)仅有整数解(x,y)＝(±16,2)

2 结语

不定方程的整数解问题是一个悠久的研究课题,许多数学家都有所研究,推进了不定方程整数解问题的发展,本文研究了x2＋256＝4yn(n＝3, 5,7)的整数解问题,得出了不定方程x2＋256＝4yn当n＝3仅有整数解(x,y)＝(0,4),n＝5无整数解,n＝7时仅有整数解(x,y)＝(±16,2)的结论和证明,接下来希望能进一步研究不定方程的整数解的问题.

[1]Lebesgue V A.Surl′impossibilite en nomber entiers de equation xm＝y2＋1[J].Nouvelle Annals of Mathematics, 1850(1):178－181.

[2]Nagell T.Sur Limpossibilite de quelques equations deux indeterminees[J].Norsk Marem Fornmings Skrefter Senel, 1921(1):65－82.

[3]孙树东.不定方程x2＋64＝y13的整数解[J].吉林师范大学学报:自然科学版,2015(3):78－80.

[4]杨 全.关于不定方程x2＋16＝y9的解[J].牡丹江大学学报,2013(8):119－120.

[5]李中恢,张四保.关于不定方程x2＋16＝y11的解[J].海南大学学报:自然科学版,2009(3):216－218.

[6]张四保,吕明富.关于不定方程x2＋64＝4y13的解[J].喀什师范学院学报,2010(3):22－23.

[7]潘承洞,潘承彪.代数数论[M].哈尔滨:哈尔滨工业大学出版社,2014:34－39.

[8]李亚卓.关于2个不定方程的求解[J].高师理科学刊,2009(1):50－51.

[9]高媛媛,郭金保.关于不定方程x2＋64＝y5[J].延安大学学报:自然科学版,2010(1):6－7.

[10]张 杰.关于不定方程x2＋64＝y7的解的讨论[J].重庆工商大学学报:自然科学版,2012(3):27－28.

[责任编辑 范 藻]

Discussion on the Integer Solution to Diophantine Equation

SHANG Xu1,LI Longgang2
(1.Department of Mathematics,Zhejiang Normal University,Jin hua Zhejiang 321004; 2.Ji BangScience and Technology Education,Xi’an Shaanxi 710000,China)

By using themethod of algebraic number theory,we study the integer solution of some Diophantine equations in the Gauss domain,which has advanced the study of the Diophantine equation.

Gauss domain;Diophantine equation;integer solution;algebraic number theory

0156.2

A

1674－5248(2017)05－0007－03

2017－05－04

尚 旭(1989—),男,陕西西安人.硕士,主要从事算子代数与初等数论研究.