瑞利随机分布下滚筒截割载荷重构算法与数值模拟

张 丹，刘春生，李德根

瑞利随机分布下滚筒截割载荷重构算法与数值模拟

张 丹1，刘春生1，李德根2

(1.黑龙江科技大学 机械工程学院，黑龙江 哈尔滨 150023; 2.黑龙江科技大学 学术理论研究部，黑龙江 哈尔滨 150023)

为了获得滚筒截割载荷特性曲线，对截齿与滚筒的受力进行了分析研究，得到了截齿轴向阻力与滚筒截割载荷的数值关系，运用自制的多截齿旋转截割煤岩实验设备，进行了截齿截割煤岩实验，得到了截齿三向力曲线，建立了滚筒截割载荷随机载荷曲线重构模型，给出了载荷重构算法，利用测试数据对滚筒截割载荷进行了数值模拟，得到了滚筒截割载荷重构载荷谱。研究结果表明：实验条件下煤岩崩落周期约为0.04 s，滚筒截割载荷数值上大于滚筒上各截齿同一时刻各截割阻力之和;滚筒截割载荷与参与截割的截齿截割阻力峰值、随机分布状态、截齿位置角、煤岩崩落周期及各截齿作用位置有关;所提算法与修正离散正则化算法比较，计算速度提高了约70倍，少样本数据下，该算法精度优于修正离散正则化算法，但重构数据只在重构点处具有真实性;使用改进的FFT算法进行重构曲线数值拟合，与FFT算法相比，计算量减小为原来的1/16，计算速度提高了约27倍，拟合优度相同，均为0.94，拟合曲线在总体趋势上比较平滑，呈现月牙形，与截割厚度变化规律一致，波形特征比较容易辨识，特征值便于判断和提取。研究结果为截齿三向力与滚筒截割载荷的关联提供依据，同时为滚筒截割载荷重构及数值拟合提供高效便捷的算法。

采煤机;滚筒载荷重构;数值模拟;瑞利随机理论;截割实验

采煤机滚筒承担着截煤、装煤、喷雾降尘等工作，功率消耗占装机功率80%以上，其载荷特性对整机的工作性能有重要影响。因此，对滚筒载荷的研究一直是采煤机设计领域的热点课题。由于煤岩本身特性及井下工况的特殊性，滚筒截割载荷特性十分复杂，且实际工作中滚筒截割阻力作用点在实时变化，所以很难直接测得滚筒截割载荷，但截齿三向力可以通过多种手段获得，如实验法、计算机模拟法等，实验法更接近真实工况，获得的载荷信息更接近真实载荷。李晓豁先后研究了连续采煤机截齿随机载荷的数学模型和掘进机截割硬岩的载荷，并对截割硬岩的载荷进行了模拟研究[1-2];赵丽娟研究了含硫化铁结核薄煤层采煤机工作机构载荷问题，并基于经济截割相关理论，进行了采煤机运动学参数的优化研究[3-4];刘春生进行了单齿截割试验，建立了截割阻力数学模型，后又对镐型截齿截割阻力谱的分形特征进行了研究，并于2014年采用修正离散正则化算法，对实验获得的截齿截割煤岩载荷曲线进行了重构与推演[5-7]。上述研究中，前两者的研究均以理论研究及计算机仿真研究为手段，缺乏有效的实验载荷进行验证，后者的研究以实验曲线上各点为原始数据，其计算精度与选取的数据点个数密切相关，因此，若要获得较高的计算精度，势必导致计算量较大，运算缓慢。

笔者通过对截齿及滚筒载荷进行受力分析，深入了滚筒截割载荷与截齿轴向载荷的数学关系，基于瑞利随机理论，提出多截齿滚筒随机载荷曲线的重构思想及重构算法，以截齿轴向载荷实验曲线为依据，通过载荷作用时间及作用幅值的叠加，即可得到滚筒截割载荷重构曲线。继而采用改进的FFT算法进行数值仿真即可得到滚筒重构载荷拟合曲线。研究结果为截齿三向力与滚筒截割载荷的关联提供依据，同时为滚筒截割载荷重构提供高效便捷的算法，为采煤机整机及零部件结构设计提供依据。

1 滚筒受力分析

滚筒上的截齿按照一定次序依次截割煤岩，第i个截齿所产生的截割阻力矩为

式中，Dc为滚筒直径,mm;Zi(t)为第i个截齿的截割阻力,N。

滚筒上n个截齿产生的截割阻力矩之和为

滚筒截割阻力矩MG等于滚筒截割载荷与截割载荷作用点到滚筒中心径向距离L之积，假设截割载荷作用点与滚筒半径之间存在如下关系：L=KlDc(Kl为截齿作用点位置系数)，则有

式中，FZ(t)为滚筒截割载荷,N。

式中，Kli为第i个截齿作用点位置系数。

由于滚筒截割载荷作用点到转动中心的距离与滚筒直径比值呈现三角函数变化规律，即L在实时变化，因此Kli也在不断变化，但其值小于1，可见滚筒截割载荷数值上大于滚筒上各个截齿同一时刻截割阻力之和。

2 截割实验

2.1 载荷测试曲线

利用项目组自主研发的旋转截割煤岩实验设备，设置滚筒转速为40.8 r/min，进行截割角度为35°时的截齿三向力测试实验，其结构与测试原理可参照文献[7]。在截齿上建立空间坐标系，将截齿载荷分解为图1所示3个方向：沿截齿轴向为轴向阻力Y(t)，平行于滚筒轴线且垂直于截齿轴向(垂直于所示平面)的为径向阻力X(t)，在该平面内垂直于截齿轴向的载荷为侧向阻力X′(t)。由于实验台结构及测试条件的限制，测试三向力的传感器位于截齿齿身底部，使用轴向阻力进行后续载荷重构更具实用性。轴向阻力测试误差主要包括传感器标定误差、系统采集误差、齿身弹性变形引起的误差等，其中，传感器标定误差是误差主要来源，实验用传感器静态精度为1%～2% FS，初步估算轴向阻力测试误差小于5%。

图1 截齿受力示意Fig.1 Pick force diagram

设截割阻力与轴向阻力间夹角为β1，则由图1可知，截割阻力与轴向阻力、径向阻力具有如下函数关系：

大量研究表明，滚筒实际工作中，轴向阻力与径向阻力具有相同变化规律[8]，假设截齿轴向阻力与径向阻力具有如下关系：

式中，Ky为径向力系数。

联立式(3),(4)，截割阻力与轴向阻力之间有

实验取样时间为10 s，滚筒约旋转7周，得到截齿轴向阻力实验曲线如图2所示。由图2可知，截齿上轴向阻力在宏观上呈周期性变化，滚筒转动第1圈时，截齿刚刚接触煤岩，不存在大块煤崩落过程，伴随小块煤剥落，载荷波动频繁，但载荷值及波动值均较小，随截齿逐渐楔入煤岩，截割厚度逐渐增大，截齿上轴向阻力谱各峰值随截割厚度的增大而增大;当截割厚度达到最大值时，此时阻力谱同时达到峰值，当旋转截割实验台减速进给，截齿截割厚度逐渐减小，截齿破碎煤岩载荷也随之逐渐减小，最后1圈，截齿逐渐与煤岩分离。

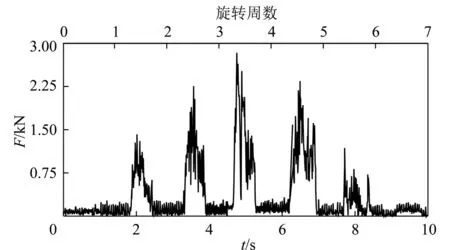
图2 截齿轴向阻力测试曲线Fig.2 Test curve of axial resistance of pick

利用上述图2所示实验曲线，便可使用截齿轴向阻力表示滚筒截割载荷。整理式(2)，(5)，得到滚筒截割载荷与截齿轴向阻力之间存在如下关系：

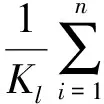
2.2 载荷测试信号的提取

单截齿阻力曲线并不能准确描述滚筒载荷特性，由于截齿排列具有一定的规律性，根据截齿排列特点及每一个截齿在滚筒上的位置，可以用实验截齿载荷曲线中所包含的截齿阻力谱信息，描述滚筒上其他截齿的载荷信息[9-10]。提取图2所示截齿最大截割厚度处的截齿轴向阻力曲线，并重新定义截割时间，将测试时间由0 s开始计数，得到截齿单周轴向阻力如图3所示。

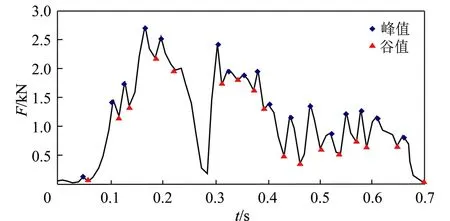
图3 截齿轴向阻力时间历程Fig.3 Timing chart of axial load of pick

截齿截割煤岩过程实质上是煤岩受到作用力不断从煤壁崩落的过程，因此，描述截齿载荷的有效信息，实际上是煤岩崩落始末时刻截齿的受力信息[11-12]。据此，以截割厚度最大处曲线作为原始数据，滤掉载荷高频信号，提取载荷峰值与谷值，可知，滚筒旋转一周过程中，截齿载荷出现17次波动，每一次峰值与谷值的形成，伴随一次煤岩的崩落过程。实验条件下，煤岩崩落周期约为0.04 s。

3 载荷时域重构模型

3.1 截齿等效截割阻力

通过上述实验方法获得的截齿轴向阻力曲线，由于含有一定的噪声干扰信号，曲线不平滑，因此需要对轴向阻力曲线进行等效处理，剔出曲线中的噪声信号并进行平滑化处理[13]，之后利用式(6)得到等效截割阻力谱。

(1)阻力谱等效模型

设z(u)为镐型截齿截割破碎煤岩等效阻力谱，f(u)为其理论阻力谱，依据B样条曲线逼近算法，提出阻力谱等效基本思想，有下述等式：

z(u)=f(u)

设Ni,p(u)是B样条曲线基函数，定义域为样条曲线节点矢量U，其数值为

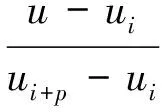
z(u)为p次B样条曲线，有[14]

式中，Pi为曲线的控制顶点。

(2)基于B样条曲线的等效算法

采煤机截齿轴向阻力谱可用二维密集扫描点进行描述，将测试数据进行等距重采样处理，得到较为光滑的数据点，计算单周轴向阻力谱节点处曲率值，并从大到小依次排列，曲率值较大的节点可以选作后续的型值点;对型值点进行参数化处理，确定节点处矢量值，对控制顶点进行反算，对型值点插值，得到型值点初始曲线;计算初始曲线与原始数据点的偏差值，若偏差不符合要求，需增加型值点，对插值曲线进行局部优化，直至偏差值符合要求。

(3)曲线型值点的选定及其节点矢量的计算

采用近似法求解曲率半径可以有效减少计算量，因此，可取任意一点di及其左右相邻两点di-1,di+1，由该3点构成一个圆弧，可将该点的曲率半径近似看作该圆弧的半径，设di到di+1矢量为A，di到di-1矢量为B，曲率半径数值可表示[15]为

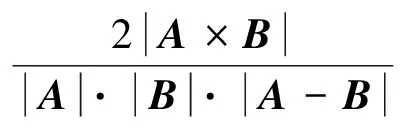
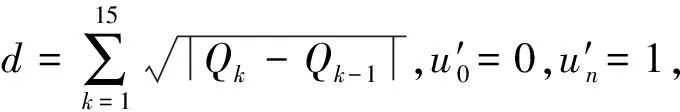
式中，k=1,2,…,14。

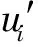
(4)控制顶点的反算和逼近偏差的计算

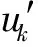
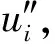
3.2 截齿截割阻力自关联模型

由于煤岩的非均质性，截齿三向阻力均具有很强的随机性，但滚筒上各截齿所受阻力存在一定的关联性[16]。假设初始接触煤岩的截齿，其截割阻力为Z1(t)，第2个接触煤岩的截齿，其截割阻力为Z2(t)，从第1齿截割煤岩到第2齿截割煤岩，其截割时间相隔为Δt，用Si表示截齿载荷随机函数，则有

Z2(t)=Z1(t+Δt,Si)

同理，有

Z3(t)=Z2(t+Δt,Si)=Z1(t+2Δt,Si)

假设t时刻，滚筒上第i个齿到第i+1个齿，其截割时间相隔为Δt，若第i个齿的截割载荷为Zi(t)，则同一时刻任一截齿截割阻力满足

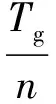
式中，Tg为滚筒转动周期,s;n为截齿个数。

4 基于瑞利分布的载荷重构算法

滚筒真实载荷与滚筒自身结构密切相关，根据获得的实验曲线，截齿三向阻力具有一定随机性，根据实验阻力曲线，可确定滚筒在某一位置的瞬时截割载荷，选择截齿位于不同位置的实验点分别进行计算，便可重构滚筒旋转一周的截割载荷曲线。

4.1 截齿截割厚度

滚筒确定后，截齿的工作载荷主要取决于截割厚度，其最大值hmax取决于采煤机牵引速度、螺旋滚筒转速及截线上的截齿数，其值[17]可表示为

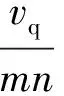
式中，vq为牵引速度,m/min;n为滚筒转速,r/min;m为截线上的截齿数。

截齿处于不同位置时，截割厚度不同。当截齿旋转至与滚筒轴线相齐的水平位置时，截齿具有最大截割厚度[18-19]。对任意截齿，其截割厚度hi为

式中，φi为第i个截齿的位置角,(°);φ为滚筒转动位置角,(°);Δφ为相邻截齿周间夹角,(°)。

4.2 瑞利随机分布

使用Matlab假设检验进行判别，实验曲线符合瑞利分布，文献[16]也有相同结论。瑞利分布中连续随机变量ξ的概率密度[20-21]为

瑞利分布的均值

瑞利分布方差

如果ξ为[0，1]区间均匀分布的随机数列，令

整理瑞利分布随机数η，而

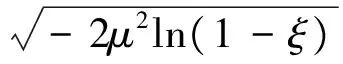
4.3 基于瑞利分布的滚筒截割载荷重构

截割过程中，伴随大块煤崩落，同时参与破煤的截齿，其截割阻力具有一定的随机性，其值与大块煤崩落周期有如下关系

式中，t为截齿截割时间,s;Ti为第i个截齿截煤过程中大块煤崩落周期,s;R(i)为瑞丽分布随机数,其值为0～1,i=0,1,…,n0,反映了同一时刻不同截齿所处的截割阻力状态;n0为同时参与截割的截齿数。

将式(8)代入式(5)，滚筒截割载荷可表示为

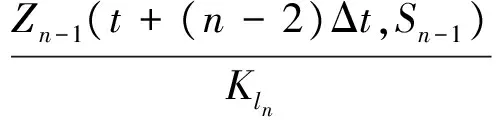
煤岩破碎过程中伴随小块煤至大块煤崩落的重复性行为。同样截割厚度下，大块煤岩崩落时，截割阻力达到最大值，假设实验煤岩与真实煤岩具有相同截割阻抗A，则实验截齿与滚筒上第i齿的最大截割阻力分别为

式(9),(12),(13)代入式(10)整理有

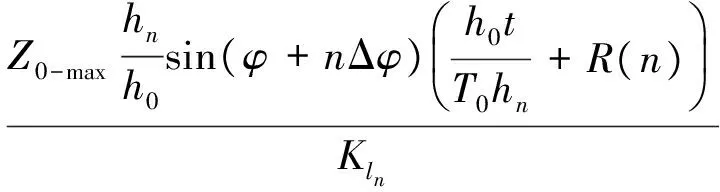
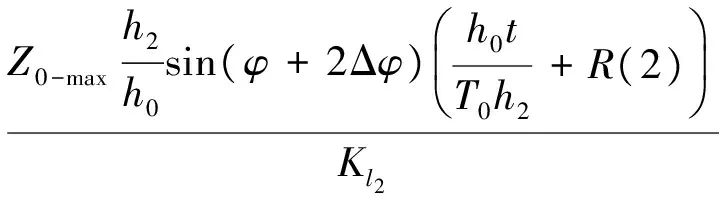
该式即为基于瑞利随机理论的滚筒截割载荷重构表达式，可见，滚筒截割载荷与参与截割的截齿截割阻力峰值、随机分布状态、截齿位置角及煤岩崩落周期有关，也与各截齿作用位置有关。

5 载荷重构算法的数值模拟

5.1 载荷时域重构

以镐型截齿楔入角为β=35°的截齿破碎煤岩实验载荷曲线为处理对象，其等距采样时间为ΔT=0.02，N=36，取[δ]=0.1，设偏差许可值为[δ]，如果有δj>[δ]，则将Dj点作为新增型值点。对B样条曲线进行优化，直至所有点满足δi≤[δ]，求得的控制顶点如图4所示，实验轴向载荷曲线的等效截割阻力如图5所示。

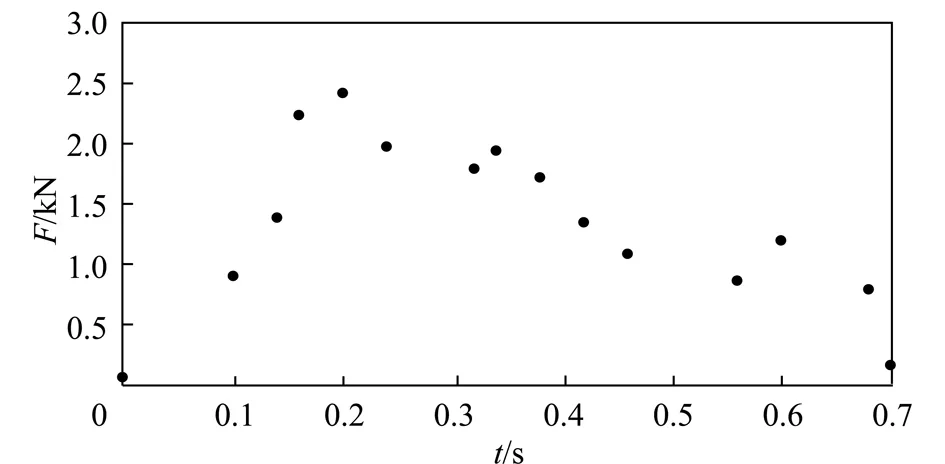
图4 截齿截割阻力B样条曲线控制点Fig.4 Cutting resistance B-spline curve control points

图5 截齿等效截割阻力曲线Fig.5 Equivalent cutting resistance curve of pick

滚筒上截齿按一定次序截割煤岩，截齿排列对滚筒截割载荷有一定影响。滚筒上截齿包括端盘截齿和叶片截齿，假设端盘截齿受力大小与叶片截齿受力大小近似呈一定比例关系，且课题重点探索载荷变化的规律，因此可按照测试间接获得的截割阻力推算端盘截齿受力大小，忽略载荷峰值特征对载荷特性的影响。图6为某采煤机滚筒叶片截齿排列图，滚筒上共20个截齿，截线距为70 mm，螺旋升角20°。易知，同时有10个截齿进行截割煤岩，假设1号截齿即将退出截割，11号截齿即将进入截割，则第1～10号截齿正在截割煤岩，各截齿截割厚度不同，假设截割阻力大小与截割厚度近似呈线性关系，则可根据滚筒不同位置上各截齿的截割厚度，结合实验测试数据推算各截齿的截割阻力。

图6 某采煤机滚筒叶片截齿排列Fig.6 Arrangement of cutting blade of shearer drum

表11～10号截齿的截割厚度
Table1Nos.1-10picksthickness

序号2，103，94，85，761截齿位置角/(°)18365472900截割厚度/mm46488212141427150

根据测得的实验曲线，大块煤崩落周期T0≈0.04s。利用本文重构算法，按时间轴等距原则，选取实验曲线中的数据，对滚筒截割载荷进行重构，得到计算点处的重构数据，如图7所示，重构曲线可通过分段函数进行描述。

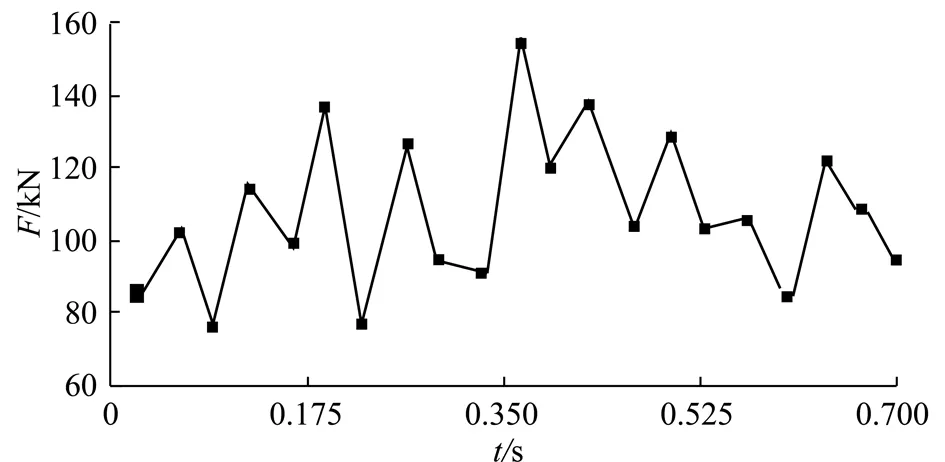
图7 滚筒载荷重构曲线Fig.7 Roller load reconstruction curve

使用上述算法与文献[7]使用的修正离散正则化算法对比情况见表2。以实验测试数据为例，从计算速度来看，由于修正离散正则化算法需要对修正稳定平稳泛函方程进行求解，而本文算法只需进行各截齿同一时刻截割力幅值的叠加，因此，本算法计算量大大减少，以21个数据点为例，其计算速度提高了约70倍，明显优于修正离散正则化算法。需要指出的是，当数据点较少时，文中算法能获得较好的计算精度。而当数据点大于21时，修正离散正则化算法具有更高的计算精度。

表2与修正离散正则化算法对比
Table2Comparisonwithmodifieddiscreteregularizationalgorithm

参 数修正离散正则化算法15212631本文算法15212631计算速度/ms72012001920312016171718计算精度/%7789919891929494

5.2 基于改进FFT算法的曲线拟合

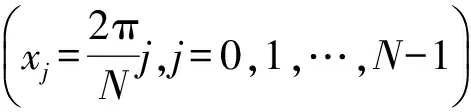
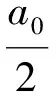
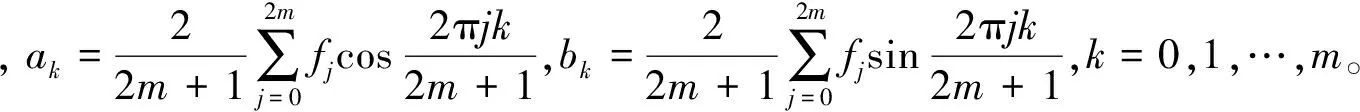
当m=n时，fj=Sm(xj)，则

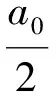
由于滚筒重构曲线中重构点之间为等分点且

eijx=cos(jx)+isin(jx)

函数族{1,eix,…,ei(N-1)x}在函数周期内正交，将eijxk组成的向量记作

能够证明，φ0,φ1,…,φN-1是正交的[23]。因此，f(x)在N个离散点上的最小二乘傅里叶逼近为

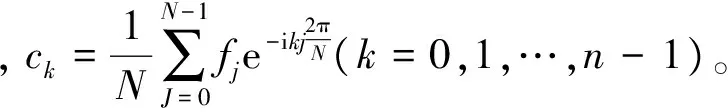
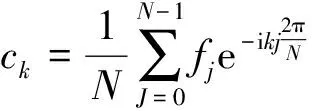
当N=23时，将k,j用二进制表示[24]为

k=k222+k121+k020=(k2k1k0)

j=j222+j121+j020=(j2j1j0)

则有

cj=c(j2j1j0),xk=x(k2k1k0)

上式可表示为

ϖ(k2k1k0)(j222+j121+j020)=

引入记号

式(16)可写为

c(j2j1j0)=A3(j2j1j0)

同理，式(17)中第2行可写为

将上式还原为十进制表示：

k=(0k1k0)=k121+k020，即k=0,1,2,3，得

同样，式(17)中第3行、第4行进行简化并还原为十进制，有

根据式(18)～(20)，由A0(k)=x(k)=xk，逐次计算即可得到cj[25]。

将式(20)推广到N=2p，则有

式中，q=1,…,p;k=0,1,…,2p-q-1;j=0,1,…,2q-1-1。

采用改进后的FFT算法与原算法对比情况见表3。改进后的FFT算法，其计算量仅为原算法的1/16，计算时间由461.9 ms减为17.4 ms，计算速度比原算法约提高了27倍，但拟合优度一致，数据点越多，这种算法的优势越明显。

利用上述算法对滚筒载荷重构曲线进行拟合，得到图8所示结果。

重构拟合曲线表达式为

表3与原算法对比结果
Table3Comparisonwiththeoriginalalgorithm

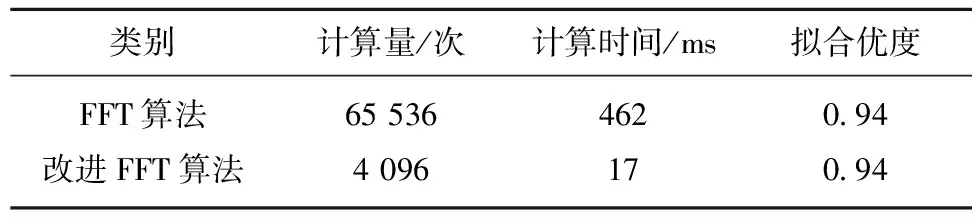
类别计算量/次计算时间/ms拟合优度FFT算法65536462094改进FFT算法409617094

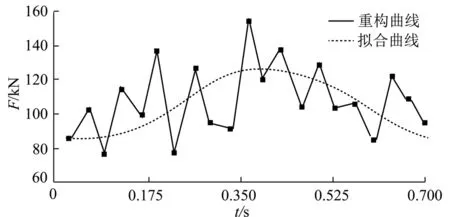
图8 滚筒载荷的傅里叶函数拟合Fig.8 Fourier function fitting of roller load

式中，ω为滚筒转动角速度,rsd/s。

其系数如下：

可以利用该曲线进行滚筒的结构设计，同时为采煤机整机的结构设计提供依据。

6 结 论

(1)进行了滚筒截割煤岩实验，截齿上轴向截割阻力在宏观上呈周期性变化，小块煤剥落过程中载荷波动频繁，但载荷值及波动值均较小，稳定截割阶段，截齿上轴向阻力峰值随截割厚度的增大而增大，实验条件下，煤岩崩落周期约为0.04 s。

(2)滚筒截割载荷数值上大于滚筒上各个截齿同一时刻截割阻力之和，瑞利随机分布下的滚筒重构载荷有效反映了滚筒截割载荷与参与截割的截齿截割阻力峰值、随机分布状态、截齿位置角、煤岩崩落周期及各截齿作用位置之间的关系。

(3)以截齿最大截割厚度处的测试载荷为依据，对滚筒载荷进行了重构，对比研究了本重构算法与修正离散正则化算法在计算速度及精度上的差别，本算法在数据点较少时，重构曲线仍能够达到较好的精度，只有当数据点大于30时，修正离散正则化算法才能达到0.9以上的精度。重构载荷曲线可通过分段函数描述，但重构曲线上的载荷数据，只在重构点处具有一致性。

(4)使用改进的FFT算法进行了重构载荷曲线拟合，改进后的FFT算法，计算量减小为原来的1/16，计算速度提高了约27倍，计算精度一致。曲线拟合优度达0.94，拟合曲线宏观趋势比较平滑，波形特征比较容易辨识，其特征值便于判断和提取，重构截割载荷曲线在总体趋势上，呈现月牙形，与截割厚度变化规律一致。

[1] 李晓豁,葛怀挺.连续采煤机截齿随机载荷的数学模型[J].中国工程机械学报,2006,4(3):262-264. LI Xiaohuo,GE Huaiting.Mathematical model of stochastic pick loads for a continuous miner[J].Chinese Journal of Counstruction Machinery,2006,4(3):262-264.

[2] 李晓豁,姜丽丽.掘进机截割硬岩的载荷模拟研究[J].中国工程机械学报,2008,6(4):415-417. LI Xiaohuo,JIANG Lili.Excavator loading simulation for hard-rock cutting[J].Chinese Journal of Counstruction Machinery,2008,6(4):415-417.

[3] 赵丽娟,董萌萌.含硫化铁结核薄煤层采煤机工作机构载荷问题[J].煤炭学报,2009,34(6):840-844. ZHAO Lijuan,DONG Mengmeng.Load problems of working mechanism of the shearer in Containing pyrites and thin coal seam[J].Journal of China Coal Society,2009,34(6):840-844.

[4] 赵丽娟,刘旭南,马联伟.基于经济截割的采煤机运动学参数优化研究[J].煤炭学报,2013,38(8):1490-1495. ZHAO Lijuan,LIU Xunan,MA Lianwei.Optimization research on shearer’s kinematic parameters based on economical cutting[J].Journal of China Coal Society,2013,38(8):1490-1495.

[5] 刘春生,李德根.基于单齿截割试验条件的截割阻力数学模型[J].煤炭学报,2011,36(9):1565-1569. LIU Chunsheng,LI Degen.Mathematical model of cutting force based on experimental conditions of single pick cutting[J].Journal of China Coal Society,2011,36(9):1565-1569.

[6] 刘春生,王庆华,李德根.镐型截齿截割阻力谱的分形特征与比能耗模型[J].煤炭学报,2015,40(6):2623-2628. LIU Chunsheng,WANG Qinghua,LI Degen.Fractal characteristic and specific energy model of conical picks cutting resistance spectrum[J].Journal of China Coal Society,2015,40(6):2623-2628.

[7] 刘春生,任春平,李德根.修正离散正则化算法的截割煤岩载荷谱的重构与推演[J].煤炭学报,2014,39(5):981-986. LIU Chunsheng,REN Chunping,LI Degen.Reconstruction and deduction of cutting coal and rock load spectrum onmodified discrete regularization algorithm[J].Journal of China Coal Society,2014,39(5):981-986.

[8] 刘春生,于信伟,任昌玉.滚筒式采煤机工作机构[M].哈尔滨:哈尔滨工程大学出版社,2010:61. LIU Chunsheng,YU Xinwei,REN Changyu.Working mechanism of drum shearer[M].Harbin:Harbin Engineering University Publishing House,2010:61.

[9] ZHANG Dan,HU Shenghai,LIU Xuntao.Level mobile shot blasting machine shot blasting wheel in the dynamic simulation based on ADAMS[J].Applied Mechanics & Materials,2011,148-149:837-841.

[10] ZHANG Dan,HU Shenghai,LIU Chunsheng.Modeling and kinematics simulation of shearer’s travelling mechanism based on virtual prototyping technology[J].Advanced Materials Research,2013,655-657:396-399.

[11] 苏秀平,李威,徐志鹏.采煤机工作面截割试验分析[J].煤炭学报,2013,38(9):1681-1685. SU Xiuping,LI Wei,XU Zhipeng.Test analysis of shearer cutting at coal face[J].Journal of China Coal Society,2013,38(9):1681-1685.

[12] 刘春生,韩飞,王庆华.双联镐齿截割煤岩力学特性的数值模拟[J].黑龙江科技大学学报,2015,25(5):476-481. LIU Chunsheng,HAN Fei,WANG Qinghua.Numerical simulation of mechanical behavior on duplex picks cutting coal[J].Journal of Heilongjiang University of Science & Technology,2015,25(5):476-481.

[13] 孔宪仁,熊怀,李海勤.一种Hilbert变换法在非线性系统分析中的应用[J].机械工程学报,2016,52(19):95-101. KONG Xianren,XIONG Huai,LI Haiqin.The modified method of hilbert transform and application in nonlinear vibration analysis[J].Chinese Journal of Mechanical Engineering,2016,52(19):95-101.

[14] ZHANG Dan,HU Shenghai,LIU Chunsheng.Elastic model of shearer walking mechanism and traction characteristics[J].Joural of Applied Mathematics and Statistics,2013,51(24):442-453.

[15] ZHAO L,LAN J.Dynamic simulation for transmission system of coal winning machine cutting part.Zhendongyu Chongji[J].Journal of Vibration and Shock,2014,33(23):106-110.

[16] 张丹,田操,孙月华.销轨弯曲角对采煤机行走机构动力学特性的影响[J].黑龙江科技大学学报,2014,24(3):262-266. ZHANG Dan,TIAN Cao,SUN Yuehua.Effect of bending angle of conveyor on dynamics of shearer running gear[J].Journal of Heilongjiang University of Science & Technology,2014,24(3):262-266.

[17] 刘春生.滚筒式采煤机理论设计基础[M].徐州:中国矿业大学出版社,2003:136. LIU Chunsheng.Design theory on drum shearer[M].Xuzhou:China University of Mining and Technology Press,2003:136.

[18] 刘春生,任春平,王磊.等切削厚度的镐型齿旋转截割煤岩比能耗模型[J].黑龙江科技大学学报,2016,26(1):53-57. LIU Chunsheng,REN Chunping,WANG Lei.Model of energy consumption based on conical pick rotary cutting coal rock for cutting thickness[J].Journal of Heilongjiang University of Science & Technology,2016,26(1):53-57.

[19] 吴卫东,单长斌.采煤机截割部扭矩轴对传动系统动态特性的影响[J].黑龙江科技大学学报,2014,24(4):394-398. WU Weidong,SHAN Changbin.Dynamics performance analysis of shearer cutting part torque shaft to transmission system[J].Journal of Heilongjiang University of Science & Technology,2014,24(4):394-398.

[20] GUNES Yilmaz N,YURDAKUL M,GOKTAN R M.Prediction of radial bitcutting force in high-strength rocks using multiple linear regressionanalysis[J].International Journal of Rock Mechanics & Mining Sciences,2007,44:962-970.

[21] RAJAN M P.Convergence analysis of a regularized approximation for solving Fredholm integral equations of the first kind[J].J.Math.Anal.Appl.,2003,27(9):522-530.

[22] ALI Ashtari.Signal processing methods for high resolution microwave image reconstruction[D].Winnipeg:University of Manitoba,2009.

[23] GU Tao,LI Xu.New equipment of distinguishing rock from coal based on statistical analysis of fast fourier transform[A].Xiamen:Global Congress on Intelligent Systems[C].2009:269-273.

[24] MITRA P,VENAYAGAMOORTHY G K.An adaptive control strategy for dstatcom applications in an electric ship power system[J].IEEE Power Electronics Society,2010,25(1):95-98.

[25] LUH G C,CHUEH C H.Multi-modal topological optimization of structure using immune algorithm[J].Computer Methods in Applied Mechanics and Engineering,2004,193:4035-4055.

ReconstructionalgorithmanditsnumericalsimulationfordrumloadbasedonRayleighstochastictheory

ZHANG Dan1，LIU Chunsheng1，LI Degen2

(1.SchoolofMechanicalEngineeringHeilongjiangUniversityofScienceandTechnology,Harbin150023,China; 2.DepartmentofAcademicResearch,HeilongjiangUniversityofScienceandTechnology，Harbin150023,China)

In order to obtain the drum cutting load characteristic curve,the relationship between the axial resistance of picks and cutting load of drum was obtained by analyzing the force of pick and drum.The experiment was carried out that the coal was cut with multiple picks rotation cutting by using self-made laboratory equipment.And the picks force curve was obtained,the drum random load spectrum reconstruction model was established and the load reconstruction algorithm was presented.The drum cutting load was simulated by using the test data and the load spectrum of drum cutting load was obtained.The results show that the coal caving cycle is about 0.04 s under the experimental conditions,and the drum cutting resistance is greater than the one of the picks at the same moment.The drum cutting resistance is related to the picks resistance peak,random distribution,pick position angle,coal caving cycles and cutter tooth position.Compared with the modified discrete regularization algorithm,the computational speed is improved by about 70 times,and the accuracy of the algorithm is better than that of the modified discrete regularization algorithm under less sample data.However,the reconstructed data only have the authenticity at the reconstruction point.Improved FFT algorithm that the amount of calculation is reduced to the 1/16 of original and the calculation speed is increased by about 27 times with the same accuracy.The fitting curve is smooth in the overall trend,showing crescent shape,consistent with the cutting thickness variation,the fitting goodness is 0.94,the waveform characteristic is easy to identify,and the eigenvalue is easy to judge and extract.The results provide the basis for the correlation of the three-direction force and the drum cutting load,and provide an efficient and convenient algorithm for the drum cutting load reconstruction.

shearer;load reconstruction;numerical simulation;Rayleigh stochastic theory;cutting experiment

10.13225/j.cnki.jccs.2016.1726

TD421.6

:A

:0253-9993(2017)08-2164-09

黑龙江省自然科学基金资助项目(QC2015053);哈尔滨科技局创新人才基金资助项目(2015RAQXJ017);国家自然科学基金资助项目(51674106)

张 丹(1982—)，女，黑龙江双城人，副教授，博士。E-mail:bishe_2006@163.com

张丹，刘春生，李德根.瑞利随机分布下滚筒截割载荷重构算法与数值模拟[J].煤炭学报,2017,42(8):2164-2172.

ZHANG Dan，LIU Chunsheng，LI Degen.Reconstruction algorithm and its numerical simulation for drum load based on Rayleigh stochastic theory[J].Journal of China Coal Society,2017,42(8):2164-2172.doi:10.13225/j.cnki.jccs.2016.1726