大倾角煤层采动裂隙演化规律
2017-09-25冯锦艳刘旭杭于志全
冯锦艳,刘旭杭,于志全
(北京航空航天大学 交通科学与工程学院,北京 100191)
大倾角煤层采动裂隙演化规律
冯锦艳,刘旭杭,于志全
(北京航空航天大学 交通科学与工程学院,北京 100191)
通过离散元UDEC数值模拟计算,分析了大倾角煤层开采过程中,扰动岩体裂隙的演化规律,同时采用相似材料模拟实验结果验证了数值计算结果的可靠性。大倾角煤层采动岩体裂隙发展初期以平行于工作面倾向的离层裂隙为主,后期离层裂隙的高度基本恒定,竖向裂隙扩展加速,直至延伸到地表,形成错断式裂缝和塌陷坑。在此基础上,建立了大倾角煤层采动裂隙分形维数D和采深的关系式,以及逾渗概率p和采深的关系式,实现了定量描述裂隙的演化规律。通过拟合分形维数D和逾渗概率p的关系式,可求得分形维数的峰值,进而可求得对应的采深,此采深即为破碎覆岩压密沿倾斜方向重新形成稳定结构所需的采深。计算结果可用于预先估算大倾角煤层开采埋深范围内是否可形成基本顶稳定结构,进而可采取不同的措施指导工作面的安全开采以及巷道的合理支护。
大倾角煤层;裂隙;分形维数;逾渗概率;稳定结构
煤层倾角是确定采煤方法的重要因素之一,随着综合机械化采煤技术的不断进步,当综采技术逐渐向倾斜煤层和急倾斜煤层开采拓展时,开始出现“大倾角煤层”称谓,中国按倾角的三类划分方法已不能满足开采实践与学术发展的要求。目前,多数文献认为“大倾角煤层”是指倾角为35°~55°的煤层,是倾斜和急斜煤层的一部分[1-3]。国际主要采煤国家(前苏联、美国、德国、波兰等)将倾角介于35°~55°的煤层称为大斜或陡斜煤层,这与中国的大倾角煤层称谓一致。
大倾角煤层约占中国煤炭探明储量的20%以及产量的10%,受特殊成煤环境的控制,50%以上的大倾角煤层为无烟煤和优质焦煤,是中国保护性开采的稀缺煤种。在经济发展相对滞后的西部地区,煤炭资源开发已成为西部地区区域经济发展的重要支柱,而西部矿区50%以上的矿井存在大倾角煤层,大倾角煤层占煤炭总储量的30%左右[3],如主要产煤省(区)的云南、贵州、四川、重庆、新疆、宁夏、甘肃等,要提高煤炭产业技术的经济效益,实现安全开采,就必须解决大倾角煤层开采中遇到的各种难题。
在经济快速发展的中国东部地区,大强度开采方式已经使许多矿区的浅部资源(储量)接近枯竭,如山东充州矿区、河北邢台矿区和开滦矿区、安徽淮南和淮北矿区、江苏徐州矿区、上海大屯矿区等,矿区必须转向复杂的大倾角或急倾斜煤层开采,要保持这些矿区高产高效和可持续发展同样需要解决大倾角煤层开采中遇到的各种问题。在老工业基地东北地区,鹤岗矿区一直致力于大倾角(急倾斜)煤层开采,双鸭山矿区的主力矿井也面临着条件异常复杂的大倾角煤层开采问题,要振兴这些区域的工业经济,就必须振兴其支柱产业—煤炭企业的经济发展。由此可见,大倾角煤层的安全开采问题是资源开发中的重大工程问题。
大倾角煤层是国际采矿界公认的难采煤层,是世界范围内综合机械化开采的“技术禁区”。早在20世纪七八十年代,前苏联、德国、法国、英国和波兰开展了相关研究,西班牙和捷克等也做了一些工作,但其综合机械化开采基础理论、核心技术和关键装备研究等一直未取得突破。近20多年来,中国历经几代科研和技术工作者的努力,如石平五[4]、章黎明[5]、杨印朝[6]、解盘石[7]、王红伟[8]、王金安[9-10]等许多科研人员的努力解决了大倾角煤层走向长壁综合机械化开采岩层控制基础理论问题,攻克了综合机械化开采关键技术,自主研发、制造了大倾角煤层综合机械化开采装备,建立了完善的工作面安全防护体系,形成了大倾角煤层走向长壁综合机械化开采理论和技术体系,这对中国乃至全世界的大倾角煤层开采具有重要意义。
大倾角煤层实现综合机械化开采的同时,受到许多安全问题的困扰,如瓦斯泄漏、底板突水、地表水入渗、地面塌陷和地表裂缝等,这些安全问题均和扰动岩体的裂隙演化规律密切相关。煤岩体中的裂隙场是流体渗透和运移的主要通道和富集区,如何定量或定性描述煤岩体裂隙网络的演化规律,一直是岩体力学领域关切的重大问题之一。
20世纪七八十年代,MNADELBROT[11]创立了分形几何学,利用分形维数描述自然界不规则及无序的现象和行为。AVILES[12],XIE[13-14],BABADAGLI[15]等的研究表明,岩体中的采动裂隙分布具有分形特征。中国的研究人员谢和平[16]、YU[17]、周宏伟[18]、王志国[19]等同样揭示了采动岩体裂隙网络具有分形特性,并给出了采动覆岩裂隙网络分形维数与采宽间的统计关系。除此之外周福军等[20]建立了二维、三维计算机裂隙网络模型,并且研究了岩体不连续面分布的分形特征;王国艳等[21]利用RFPA 软件揭示了采动岩体的裂隙网络分形特征。
除了分形方法外,逾渗理论(Percolation)也被引入用于描述覆岩裂隙的演化规律,它是处理强无序随机几何结构的重要方法之一,从本质上讲属于概率论的一个分支,概念最早是由 BROADBENT 等[22]在 1957 年提出,用于研究流体在随机介质中的渗流问题。冯增朝等[23-24]建立了煤体孔隙-裂隙的逾渗研究方法,并且研究了低渗透煤层的瓦斯渗透性;栗东平等[25]分析了水平煤层采动煤岩体裂隙网络的演化特征,得到了逾渗概率和分形维数的变化关系。
可见,国内外学者对裂隙网络的分形及逾渗特征做了大量研究,揭示了采用逾渗方法和分形理论研究开采岩层移动和裂隙演化规律的可行性和科学性,但对大倾角煤层开采条件下的采动岩体裂隙网络逾渗和分形特征以及两者间的关系研究还不多见。鉴于此,本文结合某45°大倾角煤层工作面,开展数值模拟研究,对开采扰动煤岩体的裂隙网络逾渗与分形特征进行研究,以期能够定量描述采动岩体裂隙的发展规律。
1 工程概况
以甘肃省某矿井煤层工作面为例,煤层倾角45°,地表为12 m厚的黄土,有1煤和2煤两层主采煤层,主采煤层水平间距60 m,其间为粗砂岩细砂岩互层,1煤直接顶为8 m厚的粉砂岩,下有0.5 m厚的高炭质泥岩伪顶,极易垮落,基本顶为中粗细砂岩,厚度大于25 m,直接底为0.8 m厚的泥岩,基本底为18 m厚的粗砂岩。
矿井采用走向长壁综采放顶煤采煤法从地下埋深-150 m水平开采,一次垂直采高50 m,每个水平留有垂直高15 m的煤柱,工作面走向长400 m。
2 数值计算模型及参数
根据所选区域垂向剖面的地形特征、地质条件以及岩体结构特点,采用UDEC2D进行数值模拟计算,地质模型如图1所示,模型尺寸长×宽=1 300 m×495 m。模型两侧设置水平约束,模型底侧固定、顶面自由。回采开挖过程为:在阶段水平内采用自左向右的扒皮式回采,阶段水平间采用自上而下的下行式一次采全高垮落式放顶煤开采模式,主采煤层的开采顺序如图2所示,为了更好地探索采动岩体的裂隙。数值计算采用的参数见表1,2。

图1 垂向剖面地质模型示意Fig.1 Geological model diagram of vertical section
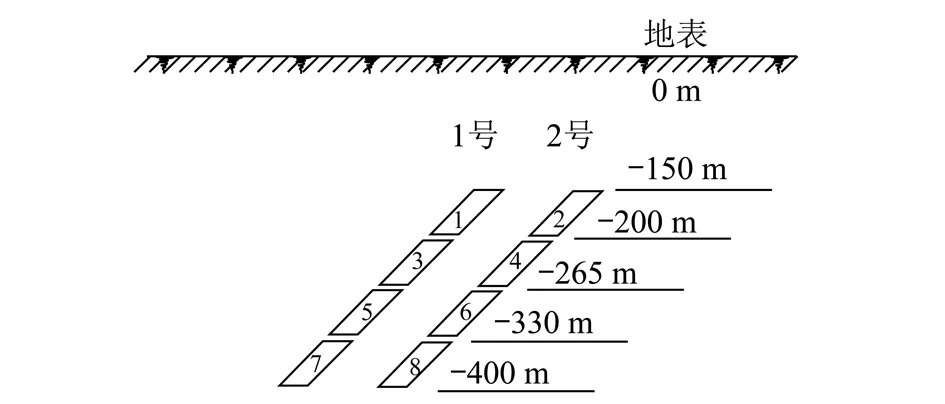
图2 主采煤层开采顺序示意Fig.2 Sketch map of step-by-step excavation process in main mineable coal seam
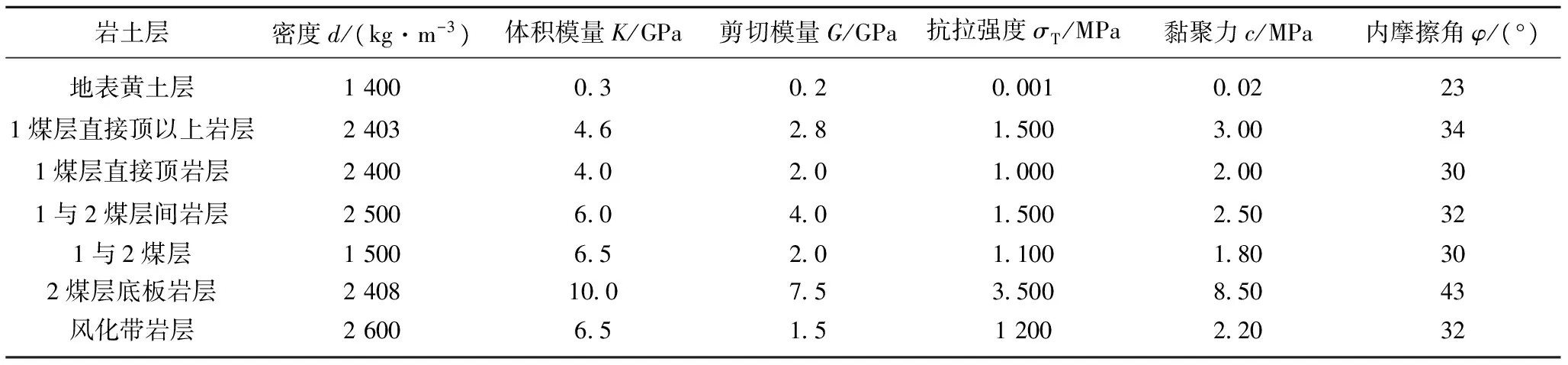
岩土层密度d/(kg·m-3)体积模量K/GPa剪切模量G/GPa抗拉强度σT/MPa黏聚力c/MPa内摩擦角φ/(°)地表黄土层140003020001002231煤层直接顶以上岩层240346281500300341煤层直接顶岩层240040201000200301与2煤层间岩层250060401500250321与2煤层150065201100180302煤层底板岩层240810075350085043风化带岩层26006515120022032
表2断层与节理力学参数
Table2Mechanicsparametersoffaultsandjoints

岩土层体积模量K/GPa剪切模量G/GPa抗拉强度σT/MPa黏聚力c/MPa内摩擦角φ/(°)地表黄土层03020001002201煤层直接顶以上岩层60400100120151煤层直接顶岩层40200020101与2煤层间岩层40300600140281与2煤层60401500250322煤层底板岩层100100250065040风化带岩层7040100016030
3 采动岩体裂隙计算结果分析
图3给出了由数值模拟计算得到的开采扰动岩体裂隙演化图。从图3可以看出,当开采埋深较小时(-200 m),上覆岩层主要产生平行于工作面倾向的离层裂隙,裂隙带高度为90 m左右。随着大倾角煤层开采深度的增加,上覆岩层裂隙带高度逐渐增加,当开采埋深为-320 m时,离层裂隙高度为170 m左右;当开采埋深为-400 m时,离层裂隙带高度为220 m左右,此时离层裂隙贯穿至地表。由此可见,大倾角煤层采动岩体裂隙包含平行于工作面的离层裂隙和垂直于工作面的竖向裂隙两种,当离层裂隙垂直于工作面发展到一定高度后,可与竖向裂隙结合贯穿至地表。

图3 采动岩体裂隙Fig.3 Fractures evolution of mining rocks
计算结果同时揭示出,多个主采煤层之间的裂隙扩展速度小于工作面上覆扰动岩体的裂隙扩展速度。
为了验证数值计算结果的准确性,同时进行了相似材料模拟实验。试验结果显示,随着开采深度的增加,裂隙逐渐扩张,当开采到埋深-400 m时,采动岩体离层裂隙快速发展,直至贯通地表,诱发大范围的错断和塌陷(图4),这与数值计算结果基本一致,说明了数值计算结果的可靠性,可在此基础上进行进一步分析。

图4 覆岩裂隙贯通至地表Fig.4 Fractures were through the earth’s surface
4 采动裂隙演化的分形计算
分形维数是定量表征事件分形性质的重要参数,这对于定量描述采动裂隙的演化规律具有重要意义。本文采用改变粗视化程度的方法求取分形维数,该方法适用于具有统计意义的自相似事件求取分形维数,Mandelbrot提出的方格统计法就是该法的一例。用不同尺度r的方格网覆盖所研究的覆岩裂隙,计数每一次覆盖时围岩裂隙所占有的方格数N(r),两者之间的关系为
将这种关系表示在双对数坐标系中,可以得到lgN(r)~lgr关系曲线,在双对数图中呈简单的直线,其中斜率正好为-D。
图5给出了分形研究中的覆岩裂隙网格划分示意图,根据相似材料模拟实验结果,覆岩和底板的破坏影响范围为长×宽=500 m×495 m,在此基础上,r采取了5个数量,分别为250,125,62.5,31.25和15.625 m。根据不同采深情况下的采动岩体裂隙lgN(r)~lgr曲线,可以得出分形维数D,断层和节理均按照裂隙处理。

图5 采动岩体分形几何格子覆盖法示意Fig.5 Lattice layout of mining rocks by fractal theory
将裂隙的分形维数与采深的关系绘制如图6所示,可以看出当采深小于400 m时,采动岩体裂隙的分形维数随开采深度的增加而增加,且呈线性增加趋势,拟合得到扰动岩体裂隙分形维数与埋深H的关系满足式(2):


图6 采动岩体裂隙分形维数与采深关系曲线Fig.6 Relationship between the fractal dimension and mining depth of mining rocks
5 采动裂隙演化的逾渗概率计算
为了更好地定量描述采动岩体裂隙的演化规律,为安全开采提供理论依据,同时采用逾渗方法计算了采动岩体的裂隙发展规律。
座逾渗也称为格点逾渗,是逾渗的两种基本模型之一,主要考虑的是网格中各点是否被占据的问题,每个格点被占据和不被占据的概率分别为p和1-p,同样每个格点占据概率与周围相邻格点的状态无关。对于煤岩体而言,整体可看作被裂隙和固体颗粒完全充满,由煤层开采引起的平行于煤层倾向的离层裂隙和竖向破断裂隙贯通,构成了许多连通的裂隙团,简称为团。随着开采深度的增加,裂隙逐步扩展且贯通,相邻的团形成更大的团,其中占格点最大的团称为最大团。随着最大团所包含的裂隙数逐渐增加,当其连通平面区域的两个对称边界时称为逾渗团,逾渗概率可定义为
其中,p为逾渗概率;M(S)为最大团中被占格点的数量;Sn为网格中格点的总数量。当为二维正方形网络时,S为每行(列)中所包含的网格数,此时n=2。
通过编制计算机程序,对数值模拟计算得到的裂隙网络二值图确定各个逾渗团,进而可确定最大团,屏蔽除最大团以外的逾渗团及孤立的裂隙,将仅含最大团的裂隙网络图转化为[0,1]矩阵,含有裂隙的格点转化为1,不含裂隙的格点转化为0;0的位置被固体颗粒占据,为不渗透格点。统计矩阵中1的个数,即为最大团被占格点的数量M(S),将其除以裂隙网络中格点总数即可得到逾渗概率p。工作面不同开采深度的裂隙图对应的逾渗概率p与开采埋深H之间的关系如图7所示,拟合公式为

从计算结果可以看出,随着大倾角煤层开采深度的增加,采动岩体裂隙的逾渗概率呈抛物线式增加趋势,当埋深小于330 m时,逾渗概率增加趋势稍缓,基本呈直线关系;当埋深大于330 m时,逾渗概率增加幅度加剧,说明采动裂隙加剧了连通速度。
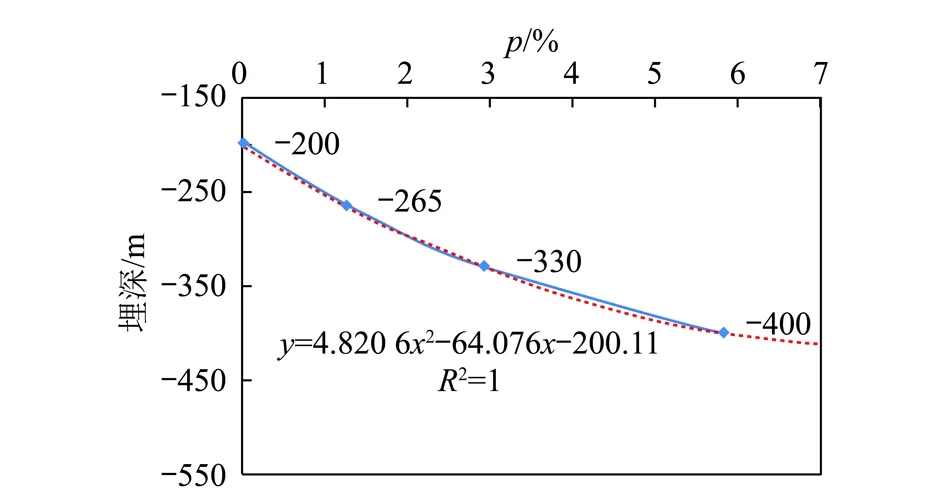
图7 采动岩体裂隙逾渗概率与采深关系曲线Fig.7 Relationship between the percolation probability and mining depth of mining rocks
6 采动裂隙的分形维数与逾渗概率的关系
由于各矿区埋深条件不同,如果能消除埋深的影响,建立采动岩体裂隙的分形维数与逾渗概率之间的关系,对于推广研究煤岩体的裂隙定量描述将具有重要意义。
由式(2)和(4)可以看出,采动岩体裂隙的分形维数与逾渗概率之间存在关系,通过联立公式可以消除开采深度的影响,有利于定量描述开采埋深小于400 m的煤岩体裂隙演化规律。经过推导,由式(2)和(4)推导出采动岩体裂隙分形维数D与逾渗概率p之间的关系为
式(5)的图形表示如图8所示,采动岩体分形维数与逾渗概率之间存在抛物线的关系式。根据公式推导预测,当采深为421 m时,分形维数达到峰值1.76;当采深小于421 m时,分形维数D随逾渗概率的增加而增加,即本工作面开采深度范围内,裂隙的分形维数一直呈增加的趋势;当采深大于421 m时,分形维数D随逾渗概率的增加而减小。计算结果充分说明了随着开采深度的增加,上部覆岩重新压密,形成稳定结构。
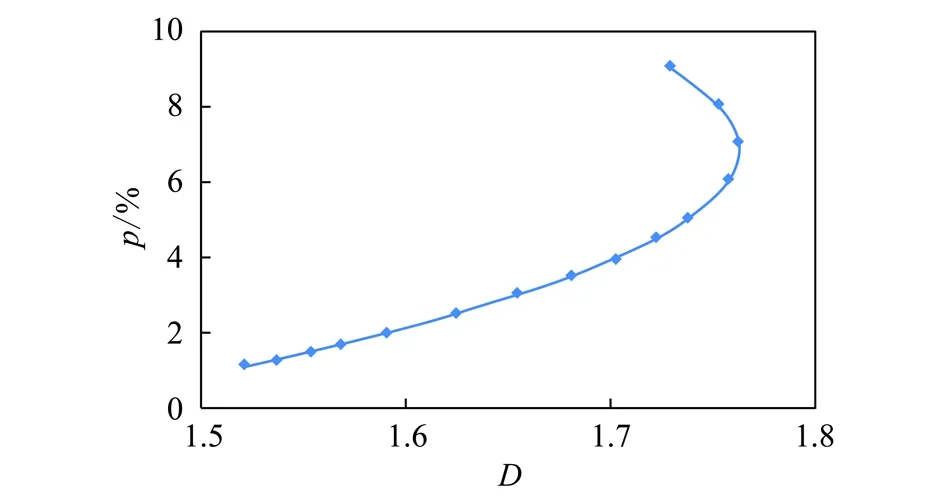
图8 采动岩体裂隙逾渗概率与分形维数关系曲线Fig.8 Relationship between the percolation probability and fractal dimension of mining rocks
图9给出了采动岩体裂隙闭合率随采深的变化曲线,可以看出,裂隙闭合率随着开采深度的增加也在增加,当采深在400 m左右时,裂隙闭合率呈现恒定值趋势,即闭合裂隙和总体裂隙都在增加,但其比率保持恒定,验证了随着开采深度的增加,大倾角煤层采动岩体重新压密,沿倾斜方向可形成新的稳定结构[26](图10)。
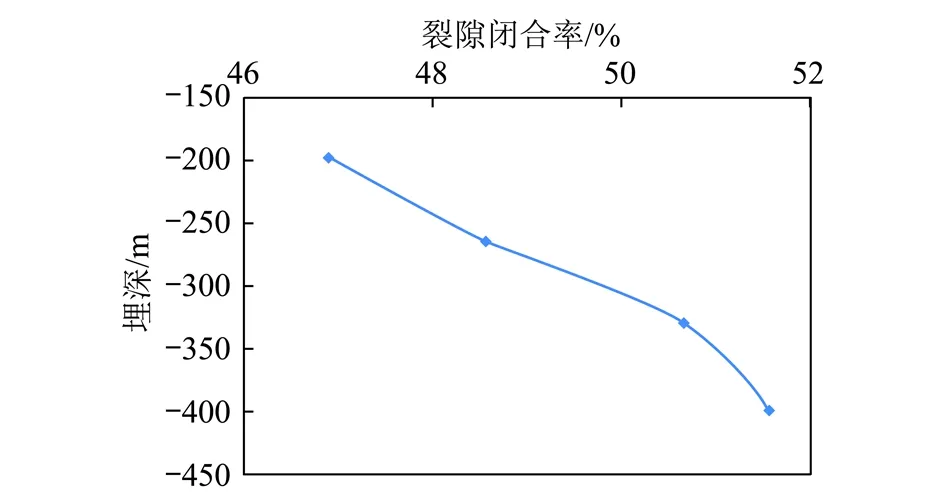
图9 采动岩体裂隙闭合率与埋深的关系曲线Fig.9 Relationship between the crack closure rate and mining depth of mining rocks

图10 采动岩体愈合的力学机制Fig.10 Healing mechanics mechanism of mining rocks
通过以上分析可知,当单一采用分形维数D或者单一采用逾渗概率p来描述采动岩体裂隙演化规律时,在开采范围内均呈增加的变化趋势,较难寻找到峰值点。为了更好地定量描述采动岩体裂隙的发展规律,寻找到分形维数的峰值点,可通过拟合逾渗概率p和分形维数D的关系式获得,依二者的关系可较容易地确定分形维数D峰值对应的开采埋深,即为基本顶沿倾斜方向重新形成稳定结构需要的采深。
根据数值模拟计算或者相似材料模拟试验结果可知,当在采深范围内基本顶可以形成承载结构时,可有效利用其稳定性实现安全开采,当基本顶在采深范围内尚未形成承载结构时,则需加强工作面和巷道的支护措施,确保安全生产。这对大倾角煤层采动岩体裂隙的演化规律研究以及安全开采提供了理论依据。
7 闭合裂隙的导水性探讨
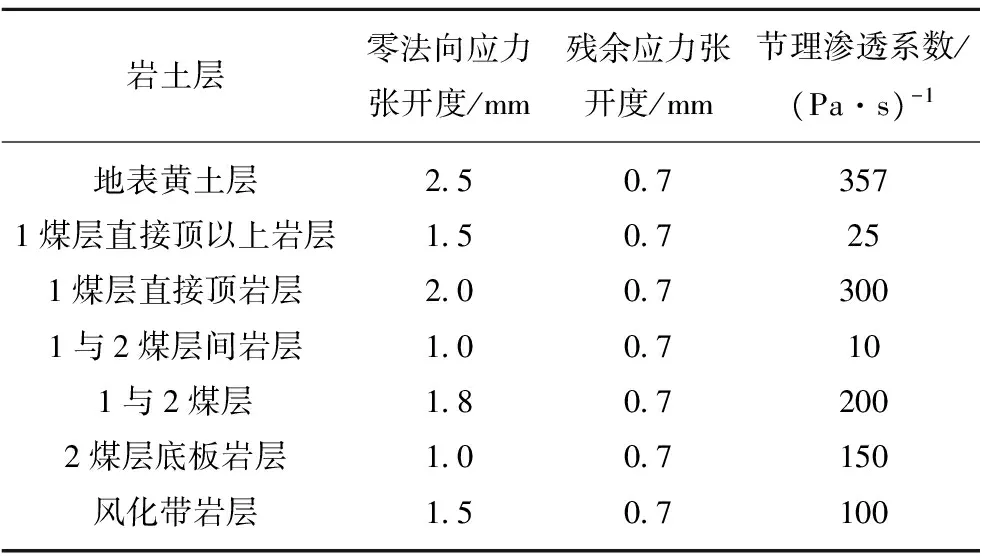
为了充分探讨大倾角煤层采动岩体裂隙的愈合机制,对扰动区域进行了渗流计算,渗流计算参数见表3。
表3水文计算参数
Table3Hydrologicalcalculationparameters
岩土层零法向应力张开度/mm残余应力张开度/mm节理渗透系数/(Pa·s)-1地表黄土层25073571煤层直接顶以上岩层1507251煤层直接顶岩层20073001与2煤层间岩层1007101与2煤层18072002煤层底板岩层1007150风化带岩层1507100
计算结果如图11,12所示,根据数值计算得到的工作面渗流矢量场,可计算工作面的总流量。计算结果显示,工作面内的流量随开采深度的增加先呈增加的趋势,当埋深在400 m时,流量出现了略微减小的趋势,验证了闭合裂隙具有了一定程度的阻水作用。

图11 开采到地下-320 m的岩体渗流矢量场Fig.11 Total water inflow when mining to the burial depth of -320 m

图12 工作面涌水量与采深的关系Fig.12 Relationship between total water inflow of the working faces and mining depth
8 结 论
(1)大倾角煤层综放开采,上部覆岩以离层裂隙为主,随着开采深度的增加,离层裂隙的高度逐渐增加,直至恒定;后期开采会进一步导致竖向裂隙加速扩展,直至连通地表,出现错断式裂缝和塌陷坑。
(2)在一定采深范围内,大倾角煤层采动岩体裂隙的分形维数D以及逾渗概率p均随采深的增加逐渐增加,说明了裂隙的不断扩展趋势。
(3)采动岩体裂隙的分形维数D与逾渗概率p之间的关系是描述裂隙演化规律的有效方法。通过拟合逾渗概率p和分形维数D的关系式获得,依二者的关系可较容易地确定分形维数D峰值对应的开采埋深,即为基本顶沿倾斜方向重新形成稳定结构需要的采深,当小于此埋深时,需加强工作面的支护,当大于此埋深时,可充分利用基本顶沿倾斜方向的稳定性结构,适当减弱支护结构,可为现场工作面安全开采以及巷道合理支护提供理论依据。
[1] 伍永平,刘孔智,贠东风,等.大倾角煤层安全高效开采技术研究进展[J].煤炭学报,2014,39(8):1611-1618. WU Yongping,LIU Kongzhi,YUN Dongfeng,et al.Research progress on the safe and efficient mining technology of steeply dipping seam[J].Journal of China Coal Society,2014,39(8):1611-1618.
[2] 伍永平,贠东风,张淼丰.大倾角煤层综采基本问题研究[J].煤炭学报,2000,25(5):465-468. WU Yongping,YUN Dongfeng,ZHANG Miaofeng.Study on the elementary problems of full-mechanized coal mining in greater pitching seam[J].Journal of China Coal Society,2000,25(5):465-468.
[3] 王红伟.大倾角煤层开采覆岩结构特征分析[D].西安:西安科技大学,2010. WANG Hongwei.Analysis of overburden structure feature in steeply dipping seam mining[D].Xi’an:Xi’an University of Science and Technology,2010.
[4] 石平五,高召宁.急斜特厚煤层开采围岩与覆盖层破坏规律[J].煤炭学报,2003,28(1):13-16. SHI Pingwu,GAO Zhaoning.The failure laws of surrounding rocks and overlying bed in the steep special thickness seam mining[J].Journal of China Coal Society,2003,28(1):13-16.
[5] 章黎明.王家山煤矿大倾角厚煤层综放采场矿压规律研究[J].煤炭科学技术,2007,35(12):22-26. ZHANG Liming.Research on ground behavior law of fully mechanized caving mining face in deep inclined seam of Wangjiashan Mine[J].Coal Science and Technology.2007,35(12):22-26.
[6] 杨印朝,徐文彬,潘卫东,等.大倾角厚煤层综采工作面设备改造与生产管理[J].现代矿业,2015(11):234-237. YANG Yinzhao,XU Wenbin,PAN Weidong,et al.The equipment modification and production management of full-mechanized coal mining in greater pitching seam[J].Modern Mining,2015(11):234-237.
[7] 解盘石,伍永平.大倾角煤层长壁大采高开采煤壁片帮机理及防控技术[J].煤炭工程,2015,47(1):74-77. XIE Panshi,WU Yongping.Mechanism and control methods of rib spalling in steeply dipping thick seam in fully-mechanized longwall mining with large mining height[J].Coal Engineering,2015,47(1):74-77.
[8] 王红伟,伍永平,曹沛沛,等.大倾角煤层开采大型三维可加载相似模拟试验[J].煤炭学报,2015,40(7):1505-1511. WANG Hongwei,WU Yongping,CAO Peipei,et al.Large scale loadable 3D-simulation tests on mining steeply dipping seam[J].Journal of China Coal Society,2015,40(7):1505-1511.
[9] 王金安,张基伟,高小明,等.大倾角厚煤层长壁综放开采基本顶破断模式及演化过程(I)——初次破断[J].煤炭学报,2015,40(6):1353-1360. WANG Jin’an,ZHANG Jiwei,GAO Xiaoming,et al.Fracture mode and evolution of main roof stratum above longwall fully mechanized top coal caving in steeply inclined thick coal seam (I):initial fracture[J].Journal of China Coal Society,2015,40(6):1353-1360.
[10] 王金安,张基伟,高小明,等.大倾角厚煤层长壁综放开采基本顶破断模式及演化过程(II)——周期破断[J].煤炭学报,2015,40(8):1737-1745. WANG Jin’an,ZHANG Jiwei,GAO Xiaoming,et al.Fracture mode and evolution of main roof stratum above longwall fully mechanized top coal caving in steeply inclined thick coal seam (II):Periodie fracture[J].Journal of China Coal Society,2015,40(8):1737-1745.
[11] MANDELBROT B B.The fractal geometry of nature[M].New York:W.H.Freeman,1982.
[12] AVILES C A,SCHOLZ C H,BOATWRIGHT J.Fractal analysis applied to characteristic segments of the San Andreas fault[J].Journal of Geophysical Research,1987,92(B1):331-334.
[13] XIE H.Fractals in rock mechanics[M].Netherlands:Balkema A A Publishers,1993.
[14] XIE H,SANDERSON D J,PEACOCK D C P.A fractal model and energy dissipation for an echelon fractures[J].Engineering Fracture Mechanics,1994,48(5):655-662.
[15] BABADAGLI Tayfun.Fractal analysis of 2D fracture networks of geothermal reservoirs in south-western Turkey[J].Journal of Volcanology and Geothermal Research,2001,11(2):83-103.
[16] 谢和平,于广明,杨伦,等.采动岩体分形裂隙网络研究[J].岩石力学与工程学报,1999,18(2):147-151. XIE Heping,YU Guangming,YANG Lun,et al.Research on the fractal effects of crack network in overburden rock stratum[J].Chinese Journal of Rock Mechanics and Engineering,1999,18(2):147-151.
[17] YU G M,XIE H,ZHAO J F,et al.Fractal evolution of a crack network in overburden rock stratum[J].Discrete Dynamics in Nature and Society,2000,5(1):47-52.
[18] 周宏伟,张涛,薛东杰,等.长壁工作面覆岩采动裂隙网络演化特征[J].煤炭学报,2011,36(12):1957-1962. ZHOU Hongwei,ZHANG Tao,XUE Dongjie,et al.Evolution of mining-induced crack network in overburden strata of longwall face[J].Journal of China Coal Society,2011,36(12):1957-1962.
[19] 王志国,周宏伟,谢和平.深部开采上覆岩层采动裂隙网络演化的分形特征研究[J].岩土力学,2009,30(8):2403-2408. WANG Zhiguo,ZHOU Hongwei,XIE Heping.Research on fractal characterization of mined crack network evolution in overburden rock stratum under deep mining[J].Rock and Soil Mechanics,2009,30(8):2403-2408.
[20] 周福军,陈剑平,牛岑岑.裂隙化岩体不连续面密度的分形研究[J].岩石力学与工程学报,2013,32(S1):2624-2631. ZHOU Fujun,CHEN Jianping,NIU Cencen.Study of discontinuity density of fractured rock masses based on fractal theory[J].Chinese Journal of Rock Mechanics and Engineering,2013,32(S1):2624-2631.
[21] 王国艳,于广明,于永江,等.采动岩体裂隙分维演化规律分析[J].采矿与安全工程学报,2012,29(6):859-863. WANG Guoyan,YU Guangming,YU Yongjiang,et al.Study on cracks fractal evolution laws of mining rock mass[J].Journal of Mining & Safety Engineering,2012,29(6):859-863.
[22] BROADBENT S K,HAMMERSLEY J M.Percolation Processes[J].Mathematical Proceedings of the Cambridge Philosophical Society,1957,53(3):629-641.
[23] 冯增朝,赵阳升,文再明.煤岩体孔隙裂隙双重介质逾渗机理研究[J].岩石力学与工程学报,2005,24(2):236-240. FENG Zengchao,ZHAO Yangsheng,WEN Zaiming.Percolation mechanism of fractured coal rocks as dual-continua[J].Chinese Journal of Rock Mechanics and Engineering,2005,24(2):236-240.
[24] 冯增朝,赵阳升,吕兆兴.强随机分布裂隙介质的二维逾渗规律研究[J].岩石力学与工程学报,2006,25(S2):3904-3908. FENG Zengchao,ZHAO Yangsheng,LÜ Zhaoxing.Research on laws of 2D percolation of fully random distribution fracture media[J].Chinese Journal of Rock Mechanics and Engineering,2006,25(S2):3904-3908.
[25] 栗东平,周宏伟,薛东杰,等.煤岩体采动裂隙网络的逾渗与分形特征关系研究[J].岩土力学,2015,36(4):1135-1140. LI Dongping,ZHOU Hongwei,XUE Dongjie,et al.Relationship between percolation and fractal properties of mining-induced crack network in coal and rock masses[J].Rock and Soil Mechanics,2015,36(4):1135-1140.
[26] 冯锦艳,王金安,朱建明,等.急倾斜长壁工作面开采老顶平衡结构阻水性能[J].煤炭学报,2009,34(2):156-158. FENG Jinyan,WANG Jin’an,ZHU Jianming,et al.The effect of water-block for the bearing structure in main roof rocks due to mining in steep long-wall seam[J].Journal of China Coal Society,2009,34(2):156-158.
Numericalsimulationstudyonthemining-inducedfractureevolutionofsteepcoalseam
FENG Jinyan,LIU Xuhang,YU Zhiquan
(SchoolofTransportationScienceandEngineering,BeihangUniversity,Beijing100191,China)
Using the discrete element numeric simulation program UDEC,the evolution law of mining-induced fractures in the mining process in steep coal seam was studied.Combined with the study of similar material simulation experiment results,the result by numerical calculation was verified.The results indicate that bed separation fissures are the main type at the initial stage,the height of the bed separation fissures remain constant and the vertical fissures speed up to extend in the later period.When the vertical fissures extend to the surface,ladder cracks and collapse pits may be formed.The relational expression between fractal dimension (D) of the mining-induced fracture and mining depth (H) was established,and the relational expression between percolation probability (p) of the mining-induced fracture and mining depth (H) was also established based on the numerical simulation,so that the evolution law of mining-induced fracture can be quantified.By fitting the relation between the fractal dimension (D) and penetration probability (p),the peak value of fractal dimension can be obtained and the corresponding mining depth,which is needed for re-forming the stable structure of broken rock masses along the dip direction,can also be obtained.The study can be used to estimate whether steep coal seam can form a stable main roof structure in the range of mining depth in advance,and then guide the rational support measures of roadway and the safe mining of working face.
steep coal seam;fracture;fractal dimension;percolation probability;stable structure
10.13225/j.cnki.jccs.2016.1859
TD823.21;TD311
:A
:0253-9993(2017)08-1971-08


国家自然科学基金资助项目(41302273)
冯锦艳(1978—),女,天津人,副教授,硕士生导师。E-mail:fengjinyan226@163.com
冯锦艳,刘旭杭,于志全.大倾角煤层采动裂隙演化规律[J].煤炭学报,2017,42(8):1971-1978.
FENG Jinyan,LIU Xuhang,YU Zhiquan.Numerical simulation study on the mining-induced fracture evolution of steep coal seam[J].Journal of China Coal Society,2017,42(8):1971-1978.doi:10.13225/j.cnki.jccs.2016.1859
