基于Euler-Lagrange方法的细粒煤脉动气流分选数值模拟
2017-09-25韦鲁滨李大虎孙铭阳朱学帅王茂源
韦鲁滨,李大虎,苗 畅,孙铭阳,朱学帅,曾 鸣,王茂源
(中国矿业大学(北京) 化学与环境工程学院,北京 100083)
基于Euler-Lagrange方法的细粒煤脉动气流分选数值模拟
韦鲁滨,李大虎,苗 畅,孙铭阳,朱学帅,曾 鸣,王茂源
(中国矿业大学(北京) 化学与环境工程学院,北京 100083)
传统的欧拉模型和离散相模型难以准确模拟细粒煤气流分选过程,为此采用DDPM(Dense Discrete Phase Model)模型,引入相体积分数和软球碰撞模型,提出了一种基于离散相体积分数和颗粒间碰撞作用的新的细粒煤气流分选过程数值模拟方法。通过数值模拟与实验室连续分选实验,研究了分选机内流场分布和6~3 mm细粒煤脉动气流分选效果。结果表明:采用DDPM模型可有效模拟细粒煤气流分选过程中颗粒相对流场的扰动作用;分选柱内流场受被分选物料的影响,速度分布和压降值较加入颗粒前变化明显,且分选机处理量越高,压降变化越明显;实验条件范围内,DDPM模型模拟得到的各密度级重产物分配率均方根误差低于3%,且相同风量时,分选机处理量越大,分选密度越高。
细粒煤;气流;分选;模拟
从多相流的角度来讲,气流分选为典型的气固两相流动体系,离散颗粒在重力、气流曳力等作用下按粒度或密度差异进行分离。目前,该技术主要用于粮食作物、电子废弃物、生活垃圾处理等领域,在矿物分选方面研究较少[1-2]。韦鲁滨等[3]对传统气流分选装置进行改进,提出细粒煤变径脉动气流分选技术,6~3 mm细粒煤分选取得了较好效果。以往关于气固两相流的数值模拟研究主要集中在流化床、旋风分离、气力输送等领域[4-6],其模拟方法主要分为两类:以多相流模型(Multiphase models)为代表的Euler-Euler方法和以DPM模型(Discrete Phase Model)为代表的Euler-Lagrange方法。Euler-Euler方法主要用于浓相流化床的数值模拟[7-9],如VOF模型、Mixture模型和Euler模型等。此类模型将颗粒相拟流体化,并近似处理为性质均一的连续介质,气相、颗粒相可相互渗透,两相均采用Euler方法描述。Euler-Lagrange方法主要用于旋风除尘、气力输送等领域的数值模拟[10-11],如DPM模型、DEM(Discrete Element Method)模型等。该类模型采用Lagrange方法对流场中每个颗粒的位置和动力学参数分别进行追踪,以求解颗粒流的运动。
目前,气流分选方面的数值模拟主要集中在流场模拟、分选机结构优化等方面。李兵、孙鹏文等[12-13]采用CFD方法对城市垃圾处理使用的气流分选机内部流场进行数值模拟,并对进风角度、入口风速等操作参数进行了优化。何亚群等[14]对阻尼式脉动气流分选机流场进行模拟,发现气流在阻尼块上部区域存在明显的加速效应。高春雨等[15]采用Euler-Euler方法,对气流分选机内部流场中固相颗粒平均速度进行了数值模拟,认为风速、固相组分的密度和粒度是影响垃圾分选效果的最主要因素。贺靖峰等[16]采用Euler多相流模型,对主动脉动气流分选回收蛭石过程进行了模拟,模拟结果与实验基本一致。然而,细粒煤气流分选过程与蛭石等分选过程相比,颗粒粒度较大、其在气相中分布不均匀,不适合采用Euler或DPM等模型进行分选过程模拟。其原因主要为,Euler-Euler方法模拟得到的多相流动结论局限于对宏观流动特征的描述[17],不能体现颗粒在流场中的差异运动行为;而DPM模型忽略了离散颗粒的体积和颗粒间相互作用[18],从而导致颗粒相体积浓度越高,模拟结果与实验值差别越大。因此,本文考虑固相体积分数与颗粒间碰撞作用,同时采用DDPM模型和DEM模型,对6~3 mm细粒煤气流分选过程进行了数值模拟,以期建立一套相对完善可靠的细粒煤气流分选数值模拟方法。
1 数学模型
变径脉动气流分选机实际分选效果与其处理量关系密切,即颗粒体积浓度和颗粒间碰撞效应显著影响其分选效果。为此,本文同时采用DDPM模型和DEM模型进行分选过程模拟,用以分别表征颗粒相的体积效应和碰撞效应。
1.1 考虑颗粒体积效应的DDPM模型
DDPM模型中气相流场的计算过程遵循连续介质假定,考虑相间质量和动量传递,其运动规律受Navier-Stocks(N-S)方程控制,且由于气相与固相间不存在质量传递,因此其质量守恒方程的源相Sy=0。DDPM模型中颗粒相体积效应的描述方法与TFM模型(Two Flow Model)[19]类似,均通过引入相体积分数来表示,即气相控制方程为
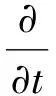
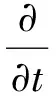
-αgp+
τg=αgμg(vg+
式中,αg为气固两相流中气相所占体积分数;ρg为气体密度,kg/m3;t为时间,s;vg为气流速度,m/s;p为静压,Pa;μg为气体动力黏度,Pa·s;vs为颗粒相速度,m/s;τ为黏性应力张量;δij为克罗内克函数;Ksg为相间动量交换系数,Ksg=Kgs。
离散相颗粒的运动轨迹通过在离散的时间步长上积分Lagrange坐标系下的颗粒运动微分方程得到,其动力学方程的积分过程中引入颗粒间碰撞力和相间作用力;同时,考虑到气流脉动引起的强烈湍流扩散,引入湍流随机脉动速度,用以体现湍流作用对颗粒运动轨迹造成的影响。忽略浮力和压力梯度力等其他较小的力,颗粒运动动力学方程为

式(4)中的各项是某颗粒受到的各类力除以该颗粒的质量,因此也可以看作对颗粒加速度的贡献。将粒群作用产生的粒间力划分成两部分Finter和Fcol。
Finter的求解采用GIDASPOW等[20]提出的颗粒流动力学理论(Kinetic Theories for Granular Flow):
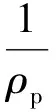
式中,τs为固相黏性应力张量。
τs=αsμs(vs+
式中,αs为固相体积分数,αs=1-αg;μs为固相动力黏度,Pa·s;其他参数具体物理意义可参照文献[20]。
CD为阻力系数,是颗粒雷诺数Rep和Wadell球形系数φ的函数,其值采用Haider-Levenspiel模型[21]近似得到
以上即为标准DPM模型的改进,称为DDPM模型,其本质上仍是基于Euler-Lagrange方法的数值模拟方法。
1.2 考虑颗粒间碰撞的DEM模型
关于颗粒间的碰撞作用,本文采用DEM模型[22]进行描述。DEM模型中,离散相颗粒与颗粒之间、颗粒与壁面之间的壁撞作用采用硬球模型[23]或软球模型[24]进行描述。由于软球模型适应性广,且可以处理多颗粒之间的接触作用,因此采用软球模型求解颗粒间碰撞问题。软球模型中,颗粒碰撞后产生微小形变,并依据变形量计算颗粒间的弹性、塑性和摩擦作用。图1为颗粒弹性碰撞示意。

图1 软球模型颗粒碰撞受力示意Fig.1 Forces resulting from particle collisions using soft-sphere approach
当两颗粒接触碰撞之后,软球模型假设其受力分为两种:一是沿碰撞方向的正向应力Fnormal,二是与碰撞方向垂直的切向应力Ffriction。
如图1所示,图中半径r1的颗粒P1和半径r2的颗粒P2的质量、坐标、速度分别为m1,x1,v1和m2,x2,v2,重叠区域厚度为δ,k为弹性系数,η为阻尼系数
其中,m12=(1/m1+1/m2)-1;χ为恢复系数,且0<χ<1。定义单位向量。
则重叠部分厚度为
颗粒P1所受正向应力可表示为
式中,d12为两颗粒圆心之间的距离,m;颗粒P2所受正向应力与颗粒P1所受正向应力方向相反。
两颗粒接触碰撞后,其切向应力为
式中,μ为摩擦因数,其值与颗粒切向相对速度有关。
特别强调,当颗粒与壁面碰撞时,认为壁面为质量无限大、半径为0的颗粒,其碰撞作用力计算方法与式(13)相同。
1.3 随机轨道模型
变径脉动气流分选机中,气流的脉动会产生强烈的湍流扩散,从而对颗粒运动产生影响。本文采用随机概率方法对湍流扩散作用进行描述,即采用随机轨道模型(Discrete Random Walk Model)[25]描述湍流扩散对颗粒运动轨迹的影响。

其中,k为湍流动能,m2/s2;θ1和θ2为计算机生成的随机数字,-1≤θ1≤1,-1≤θ2≤1,且θ1和θ2服从Gaussian分布。
通过以上DDPM,DEM和随机轨道模型的耦合求解,即可对特定条件下的细粒煤气流分选效果进行预测与评价。
1.4 计算模型离散化
变径脉动气流分选机为柱型立式分选柱,其结构经适当简化后的尺寸示意如图2所示。图2中,给料口长度为L,重产物由分选柱底部排出,轻产物由分选柱顶部排出,给料口倾斜45°方向向下。各结构参数见表1。
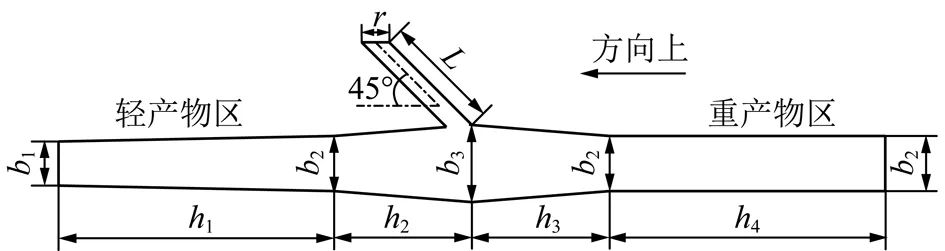
图2 分选柱结构尺寸示意Fig.2 Schematic of the separator column for simulation
通过网格绘制软件ICEM对图2所示分选机模型进行离散化处理,采用四边形划分方法进行网格划分,网格边长1 mm,网格总数为82 114个。数值算法采用Green-Gauss Node Based格式,模拟时间步长为10-4s,颗粒相时间步长10-5s,模拟时间为22 s。其中,前12 s为流场初始化阶段,后10 s为加入颗粒后的实际分选时间。气相流场模拟采用standardk-ε湍流模型,控制方程残差绝对值设为10-5。离散颗粒运动轨迹的积分采用隐式的梯形积分方法进行,为降低计算量、提升计算效率,设定连续相每迭代100步,颗粒相更新一次位置信息。
分选柱底部为均匀入流边界,顶部为压力出口边界,其余均为壁面边界。颗粒信息捕集边界条件:底部和顶部为逃逸边界,其余为反弹边界。颗粒一旦经过逃逸边界,其轨迹计算便自行终止,通过采集分选柱顶部和底部逃逸颗粒的速度、密度、粒度等信息,便可对其分选效果进行评价。
2 数值模拟及实验结果
为说明DDPM模型模拟结果的可靠性,本文分别采用DPM模型和DDPM模型进行细粒煤气流分选过程模拟,并对流场模拟结果和分选效果模拟结果进行了对比分析。
2.1 数值模拟和实验条件
2.1.1物性参数
煤样粒度和密度是影响细粒煤气流分选效果的主要物性参数。分选实验中,被分选样品为6~3 mm细粒煤,其密度组成见表2。模拟过程中,为便于统计轻、重产物逃逸信息,入射颗粒流密度为表2中各密度级平均密度,即同时入射7组不同密度的颗粒流。单位时间给入分选柱的颗粒流不同密度含量配比按照表2所示比例进行设定。
表2分选煤样密度组成
Table2Densitycomponentsoftheseparatedcoalmaterials
假定各密度级粒度组成符合Rosin-Rammler分布[26]
式中,Yd为筛上累计产率,以小数计;d为颗粒粒度,mm;dm为粒群平均粒径,mm;n为模型参数,无量纲。
令d=dm,即Yd=e-1,即可根据各密度级筛分累计曲线得到dm值,从而可知不同粒度d对应参数
其中,ni值平均即为模型参数n=(∑ni)/i,i为ni值个数。通过各密度级实验得模拟物料粒度组成见表3。
表3不同密度级Rosin-Rammler分布模型参数
Table3ModelparameterofRosin-Rammlerincoalsofdifferentdensitycomponents

密度级/(g·cm-3)120135145155170190220平均粒径/mm482477461462447434418参数n711708713699722708741
2.1.2模拟和实验条件
气流分选实验中,分选机底部鼓入由恒定主风量和辅助脉冲风量叠加而成的脉动气流,分选机内细粒煤由于气流的振荡作用实现较高精度分选。受阀门控制,脉动气流理论上为梯形脉动形式,如图3所示。

图3 脉动气流简化形式Fig.3 Simplified form of pulsing airflow
但由于电磁阀控制流量存在一定的滞后性,实际模拟时对脉动流波形进行简化,近似认为入口处周期脉动气流的速度V符合正弦波的形式:
实验和模拟条件为:主风量为恒定流235,250,260和270 m3/h,脉冲风量为10 m3/h,周期2 s,脉动阀门开闭时间比为1 s∶1 s。物料由给料口倾斜向下给入。处理量为0.018~0.076 kg/s。
2.2 流场模拟结果
2.2.1流场速度分布
图4为恒定流260 m3/h、处理量M=0.076 kg/s条件下、t=12 s时加入颗粒,分别采用DPM模型和DDPM模型模拟得到的加入颗粒前后分选机入料口附近速度分布云图。其中,t=11 s为加入颗粒之前1 s,t=16 s为加入颗粒之后4 s。

图4 加入颗粒前后分选机局部速度分布云图Fig.4 Comparison of velocity magnitude contours from different time of the simulation results from DPM and DDPM
由图4可知,采用DPM模型模拟分选过程时,加入颗粒前后,分选柱内部速度场分布变化较小,即标准DPM模型无法准确表征颗粒相对流场的影响。而采用DDPM模型模拟时,加入颗粒后,速度场分布变化明显,入料口附近速度梯度较大,离散颗粒对流场的扰动作用得以相对准确的体现。为定量分析颗粒相对流场的影响,分别测取图4中入料口下部横截面(距分选机底部高h=0.75 m)处的速度值,可得其沿水平方向变化规律,如图5所示。其中,图5(a)和(b)分别为采用DPM模型和DDPM模型模拟得到的加入颗粒前后h=0.75 m横截面处的速度变化规律。
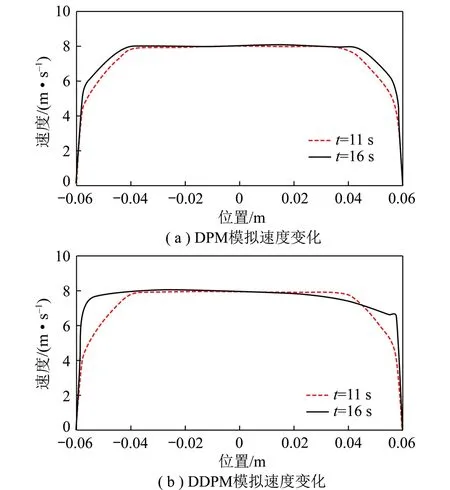
图5 h=0.75 m横截面处速度变化规律Fig.5 Changing regularity of velocity in h= 0.75 m cross-section
由图5可知,采用DPM模型模拟分选过程时,加入颗粒前后,h=0.75 m横截面处流场速度分布均较为对称,颗粒相对流场扰动作用较小。而采用DDPM模型模拟加入颗粒后的过程时,该横截面处,越靠近入料口位置,气流速度越低,流场受颗粒影响显示出一定的非对称性;同时,颗粒相对流场的扰动作用致使流场边界层厚度降低。
2.2.2分选柱压力损失
图6为恒定流260 m3/h、处理量0.018 kg/s和0.076 kg/s条件下,分别采用DPM模型、DDPM模型模拟得到的分选机内压降Δp随时间t的变化规律。

图6 分选机内压降Δp随时间t的变化规律Fig.6 Changing regularity of pressure drop Δp in the separator
图6结果表明,无论采用DPM还是DDPM模型,模拟得到的各时刻瞬时压降值差别较大,其主要原因为气流的脉动导致分选柱内流场的湍动情况复杂,压降值波动较大。图6(a)中,分选机不同处理量下,压降变化规律基本一致,即采用DPM模型模拟得到的压降主要为分选柱沿程压力损失;而图6(b)中采用DDPM模拟分选过程时,分选机处理量由0.018 kg/s提高为0.076 kg/s,压降显著增加,此时的压降除了包含沿程压力损失外,更多的是离散颗粒相加入导致风阻增大而造成的压力损失。
综上可知,采用DDPM和DPM模型模拟细粒煤脉动气流分选过程时,流场模拟结果差异较大,且DDPM模型可模拟得到颗粒相对气流场的扰动作用,流场分布模拟结果相对合理。在此基础上,下文将对两模型分选效果模拟进行详细阐述。
2.3 分选效果模拟结果
通过采用DPM模型和DDPM模型分别对6~3 mm细粒煤分选过程进行模拟,可对比不同条件下的模拟结果与实验结果。
实际分选实验条件为:处理量为M=0.018,0.076 kg/s,恒定风量分别为235,250,260和270 m3/h。表4为不同分选实验条件下精煤、尾煤的产率与灰分结果。由表4可知,采用气流分选技术排出部分矸石后,降灰效果明显,且风量较高时,其分选数量效率最高可达90%以上。
表4不同实验条件6~3mm细粒煤分选结果
Table4Resultsof6-3mmfinecoalseparationindifferentexperimentalconditions
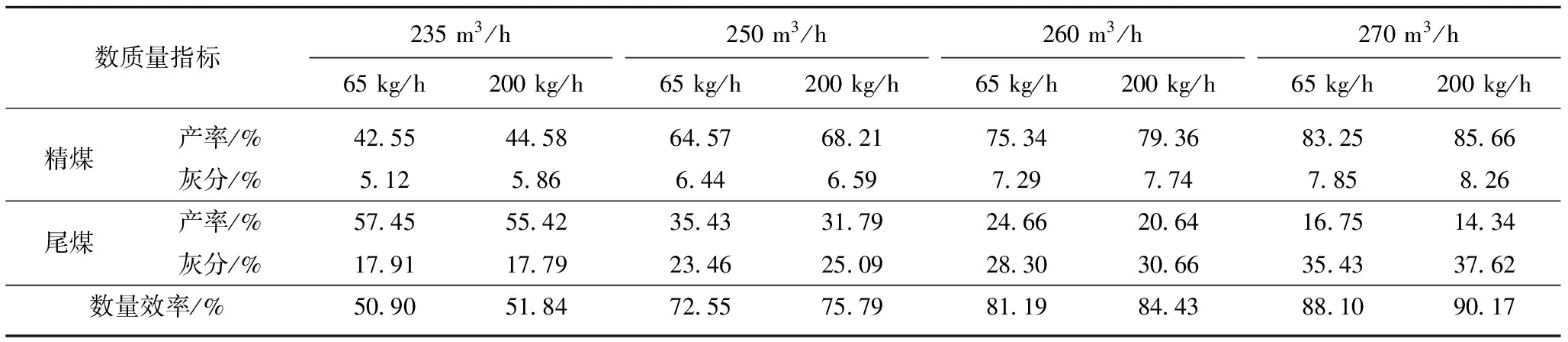
数质量指标235m3/h65kg/h200kg/h250m3/h65kg/h200kg/h260m3/h65kg/h200kg/h270m3/h65kg/h200kg/h精煤产率/%42554458645768217534793683258566灰分/%512586644659729774785826尾煤产率/%57455542354331792466206416751434灰分/%17911779234625092830306635433762数量效率/%50905184725575798119844388109017
图7为不同实验条件下,实验点与模拟分配曲线对比。由图7(a)可知,分选机处理量较低为M=0.018 kg/s时,DPM和DDPM模型的模拟结果与实验点均吻合较好,各密度级重产物分配率均方根误差RMSE分别为2.93%和2.35%,两模型模拟分配曲线基本可准确描述各密度级实际分配率。而图7(b)表明,分选机处理量增大为M=0.076 kg/s时,DPM模型模拟得到的各密度级重产物分配率总体偏大,分配率均方根误差RMSE增大为8.15%;而DDPM模型模拟得到的分配曲线仍然较好的符合实际分选结果,且RMSE=2.83%。
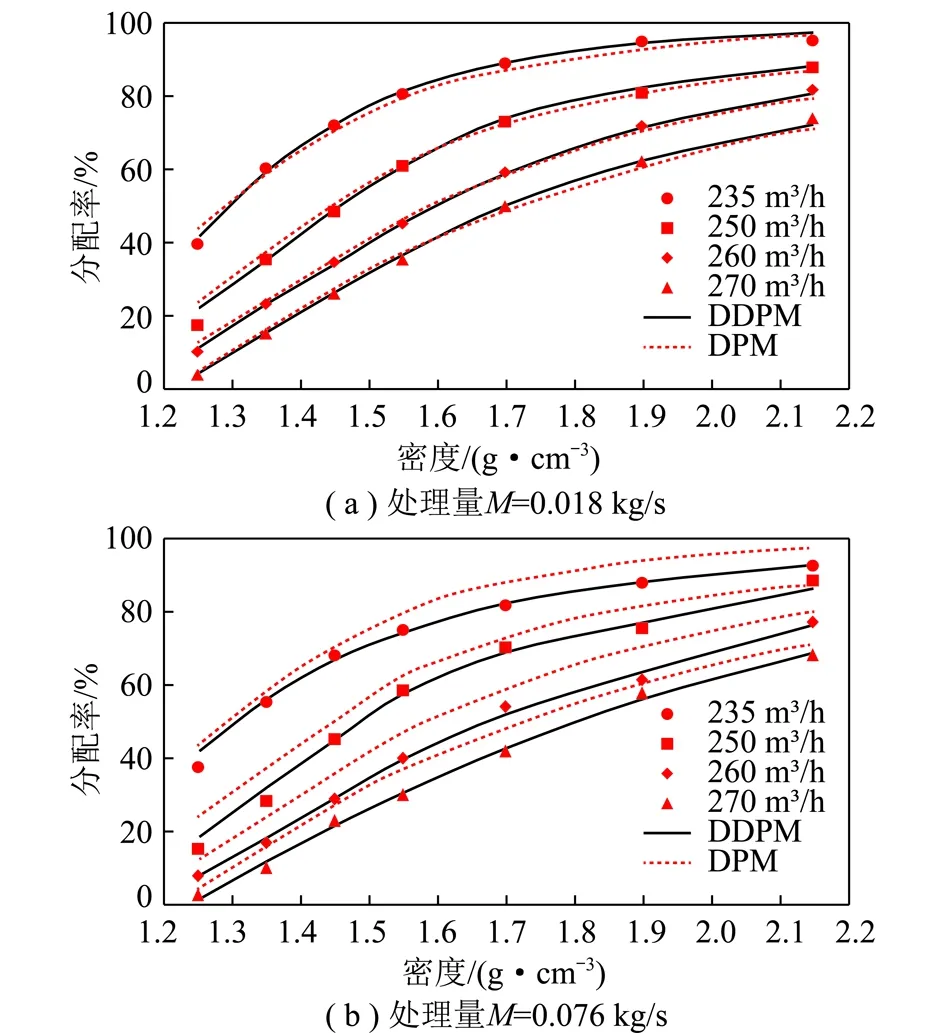
图7 实验点及模拟分配曲线Fig.7 Comparison of experimental results and simulated results
通过以上实验及数值模拟结果可知,6~3 mm细粒煤脉动气流分选过程与传统重介质分选不同,其分选效果受风量、处理量等影响较大,即在一定的分选条件下,分选密度的大小与分选机风量和处理量关系密切。总体来看,DPM模型仅适用于低处理量条件下的分选过程模拟,而DDPM模型不仅可对不同风量条件下的分选结果进行准确描述,且适用于不同处理量条件下的分选过程模拟。
3 结 论
(1)采用DDPM模型可有效模拟6~3 mm细粒煤气流分选过程中,颗粒相对流场的扰动作用:加入颗粒后,分选柱内流场均匀性下降,且在入料口下部水平横截面处,越靠近入料口位置,气流速度越低。同时,颗粒相对流场的扰动作用致使流场边界层厚度降低。
(2)DDPM模型模拟结果表明:加入颗粒前,随气流脉动速度的变化,分选柱内压降值呈周期性变化,此时的压降主要为沿程压力损失;加入颗粒后,压降值急剧增加,且分选机处理量越高,压降增加越明显,此时的压降主要为离散相颗粒加入导致风阻增大而造成的压力损失。
(3)DDPM与DPM模型的对比结果表明:相同风量时,分选机处理量越大,分选密度越高;DPM模型无法表征处理量对分选效果的影响,仅适用于低处理量条件下的分选过程模拟;DDPM模型不仅可对不同风量条件下的分选结果进行准确描述,也适用于不同处理量条件下的分选过程模拟。
[1] INNOCENTINI M D M,BARIZAN W S,ALVES M N O,et al.Pneumatic separation of hulls and meats from cracked soybeans[J].Food & Bioproducts Processing,2009,87(4):237-246.
[2] 王帅,何亚群,王海锋,等.细粒煤主动脉动气流分选试验研究[J].选煤技术,2010(3):4-8. WANG Shuai,HE Yaqun,WANG Haifeng,et al.Experimental study on separation of fine coal with active pulsating air separator[J].Coal Preparation Technology,2010(3):4-8.
[3] 赵小楠.粉煤变径脉冲气流分选技术研究[D].北京:中国矿业大学(北京),2014:84-86. ZHAO Xiaonan.Research on variable-diameter pulsed airflow separation technology for fine coal[D].Beijing:China University of Mining and Technology(Beijing),2014:84-86.
[4] SHUKLA S K,SHUKLA P,GHOSH P.Evaluation of numerical schemes using different simulation methods for the continuous phase modeling of cyclone separators[J].Advanced Powder Technology,2011,22(2):209-219.
[5] BOEMER A,QI H,RENZ U.Eulerian simulation of bubble formation at a jet in a two-dimensional fluidized bed[J].International Journal of Multiphase Flow,1997,23(5):927-944.
[6] MATUTTIS H G,LUDING S,HERRMANN H J.Discrete element simulations of dense packings and heaps made of spherical and non-spherical particles[J].Powder Technology,2000,109(1-3):278-292.
[7] SINCLAIR J L,JACKSON R.Gas-particle flow in a vertical pipe with particle-particle interactions[J].AICHE Journal,1989,35(9):1473-1486.
[8] 贺靖峰,赵跃民,何亚群,等.基于Euler-Euler模型的空气重介质流化床密度分布特性[J].煤炭学报,2013,38(7):1277-1282. HE Jingfeng,ZHAO Yuemin,HE Yaqun,et al.Distribution characteristic of bed density in air dense medium fluidized bed based on the Euler-Euler model[J].Journal of China Coal Society,2013,38(7):1277-1282.
[9] BRANDANI S,ZHANG K.A new model for the prediction of the behaviour of fluidized beds[J].Powder Technology,2006,163(1-2):80-87.
[10] 王子云,付祥钊,仝庆贵.旋风除尘器的气固两相流的数值模拟与分析[J].河南科技大学学报(自然科学版),2007,28(4):53-56. WANG Ziyun,FU Xiangzhao,TONG Qinggui.Numerical smiulation and analysis of cyclone separator with gas-solid two phase flow[J].Journal of Henan University of Science and Technology(Natural Science),2007,28(4):53-56.
[11] TSUJI Y,TANAKA T,ISHIDA T.Lagrangian numerical simulation of plug flow of cohesionless particles in a horizontal pipe[J].Powder Technology,1992,71(3):239-250.
[12] 李兵,赵由才,施庆燕,等.城市生活垃圾卧式气流分选的设计研究[J].宁波大学学报(理工版),2007,20(2):184-188. LI Bing,ZHAO Youcai,SHI Qingyan,et al.Design research on horizontal separation of MSW[J].Journal of Ningbo University(NSEE),2007,20(2):184-188.
[13] 孙鹏文,王飞,闫金顺,等.基于DPM的城市生活垃圾卧式气流分选流场仿真分析[J].内蒙古工业大学学报,2013,32(2):101-106. SUN Pengwen,WANG Fei,YAN Jinshun,et al.Simulation and analysis on horizontal flow separating field of urban garbage based on DPM[J].Journal of Inner Mongolia University of Technology,2013,32(2):101-106.
[14] 何亚群,王海锋,段晨龙,等.阻尼式脉动气流分选装置的流场分析[J].中国矿业大学学报,2005,34(5):574-578. HE Yaqun,WANG Haifeng,DUAN Chenlong,et al.Numerical simulation of airflow patterns within passive pulsing air classifiers[J].Journal of China University of Mining & Technology,2005,34(5):574-578.
[15] 高春雨,郭仁宁,纪俊红.城市生活垃圾风力分选效率研究[J].辽宁工程技术大学学报,2005,24(S1):278-280. GAO Chunyu,GUO Renning,JI Junhong.Investigation of efficiency on sorting municipal solid waste by wind power[J].Journal of Liaoning Technical University,2005,24(S1):278-280.
[16] HE J F,HE Y Q,ZHAO Y M,et al.Numerical simulation of the pulsing air separation field based on CFD[J].International Journal of Mining Science & Technology,2012,22(2):201-207.
[17] WANG Q,FENG Y,LU J,et al.Numerical study of particle segregation in a coal beneficiation fluidized bed by a TFM-DEM hybrid model:Influence of coal particle size and density[J].Chemical Engineering Journal,2015,260:240-257.
[18] ZHANG J,LI Y,FAN L S.Discrete phase simulation of gas-liquid-solid fluidization systems:Single bubble rising behavior[J].Powder Technology,2000,113(3):310-326.
[19] STUHMILLER J H.The influence of interfacial pressure forces on the character of two-phase flow model equations[J].International Journal of Multiphase Flow,1977,3(6):551-560.
[20] DING J,GIDASPOW D.A bubbling fluidization model using Kinetic-theory of granular flow[J].AICHE Journal,1990,36(4):523-538.
[21] HAIDER A,LEVENSPIEL O.Drag coefficient and terminal velocity of spherical and nonspherical particles[J].Powder Technology,1989,58(1):63-70.
[22] STRACK O D L,CUNDALL P A.The distinct element method as a tool for research in granular media[R].Department of Civil and MINERAL Engineering,University of Minnesota,1978.
[23] LUN C,SB S,DJ J,et al.Kinetic theories for granular flow:Inelastic particles in Couette flow and slightly inelastic particles in a general flowfield[J].Journal of Fluid Mechanics,1984,140:223-256.
[24] GIDASPOW D,ETTEHADIEH B.Fluidization in two-dimensional beds with a jet.2.Hydrodynamic modeling[J].Industrial & Engineering Chemistry Fundamentals,1983,22(2):193-201.
[25] GOSMAN A D,LOANNIDES E.Aspects of computer simulation of liquid-fueled combustors[J].Journal of Energy,1983,7(6):482-490.
[26] 郑钢镖,康天合,柴肇云,等.运用Rosin-Rammler分布函数研究煤尘粒径分布规律[J].太原理工大学学报,2006,37(3):317-319. ZHENG Gangbiao,KANG Tianhe,CHAI Zhaoyun,et al.Applied the Rosin-Rammler distribution function study on the law of coal dust particle-size distribution[J].Journal of Taiyuan University of Technology,2006,37(3):317-319.
NumericalstudiesofpulsingairflowseparationoffinecoalbasedonEuler-Lagrangemethod
WEI Lubin,LI Dahu,MIAO Chang,SUN Mingyang,ZHU Xueshuai,ZENG Ming,WANG Maoyuan
(SchoolofChemicalandEnvironmentalEngineering,ChinaUniversityofMiningandTechnology(Beijing),Beijing100083,China)
It is difficult to simulate the pulsing airflow separation process of fine coal accurately using the conventional numerical model,such as Eulerian Model and Discrete Phase Model.The Dense Discrete Phase Model (DDPM) of the pulsing airflow separation process of fine coal was proposed based on the volume fraction of discrete phase and Soft-sphere approach to account for the influence from the volume of particles and the forces that result from the collision of particles.The distribution of the flow field and the separation results of 6-3 mm coal particles in pulsing air classifier were simulated through numerical simulation and continuous separation experiments in laboratory.The results show that DDPM was suitable for the simulation of the pulsing airflow separation process of fine coal and it was effective to show the perturbation action on the distribution of the flow field from particle phases.The separated materials had a significant impact on the distribution of the flow field,particularly on the velocity distribution and the change of pressure drop.Moreover,the greater handling capacity of the pulsing air classifier,the more significantly change of pressure drop.Within the scope of experiment conditions,the root-mean-square error of partition coefficients of heavy product in different density fractions was less than 3% by the method of DDPM,and the greater handling capacity,the higher separation density when the blowing rate was constant.
fine coal;air flow;separation;simulation
10.13225/j.cnki.jccs.2016.1538
TD922
:A
:0253-9993(2017)08-2149-08


国家自然科学基金资助项目(51574252);国家重点基础研究发展计划(973)资助项目(2012CB214904)
韦鲁滨(1962—),男,江苏扬州人,教授,博士。Tel:010-62339616,E-mail:wlb@cumtb.edu.cn
韦鲁滨,李大虎,苗畅,等.基于Euler-Lagrange方法的细粒煤脉动气流分选数值模拟[J].煤炭学报,2017,42(8):2149-2156.
WEI Lubin,LI Dahu,MIAO Chang,et al.Numerical studies of pulsing airflow separation of fine coal based on Euler-Lagrange method[J].Journal of China Coal Society,2017,42(8):2149-2156.doi:10.13225/j.cnki.jccs.2016.1538
