热力学中的相对论变换

张 滢(美国海纳国际集团 美国 费城 PA19004)

热力学中的相对论变换

张 滢
(美国海纳国际集团 美国 费城 PA19004)

以洛伦兹变换为基础讨论了理想气体体积、压强、内能、温度、熵等热力学量的相对论变换，并从理想气体状态方程和理想气体摩尔热容的角度说明了普朗克、爱因斯坦和德布罗意给出的相对论温度变换更加合理.

理想气体 热力学量 相对论变换

1 引言

相对论力学已经十分完善，相比之下相对论热学的讨论仍然存在诸多争议.相对论变换的繁琐和热学量的统计含义使得某些问题的讨论异常复杂.迄今人们对温度这个最基本热力学量的相对论变换仍然存在着不同的看法，这也许就是热学的特征之一.相关问题的讨论有助于加深人们对热学概念的理解.

2 理想气体热力学量的相对论变换

理想气体热力学的基本内容主要涉及理想气体热力学量的含义及其相互之间的联系.气体的热力学量有状态量和过程量，状态量主要有压强、体积、温度、能量和熵等，过程量主要有功、热量等.理想气体的状态方程和热力学第一、第二定律是热力学量之间相互联系的重要形式.

2.1理想气体体积的相对论变换

不失一般性，考察形状规则、边长为L的正六面体静止于Σ′系中，根据运动方向(x轴)长度变换的洛伦兹公式[1]

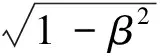
(1)

可以得到六面体体积的相对论变换为

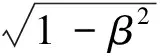
(2)

2.2理想气体压强的相对论变换

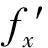
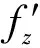
可以得出

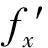
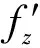
考虑到正立方体运动方向的相对论收缩，并注意到气体静止于Σ′中，在垂直于3个坐标轴方向上理想气体的压强分别为

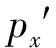
(3)

(4)

(5)

从式(3)、(4)、(5)可以得出

p=p′=p0

(6)

式(6)表明，理想气体的压强是个相对论不变量.

2.3理想气体分子平均平动动能的相对论变换

根据理想气体分子平均平动动能与压强的关系式

并注意到运动气体体积的收缩将导致其气体分子数密度的增大，可以得出

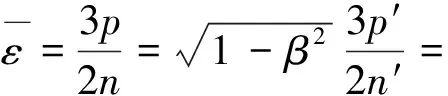
(7)

2.4理想气体内能的相对论变换

理想气体的内能等于其所有分子的动能之和，考虑到能量按自由度均分的概念，理想气体内能的相对论变换应该和式(7)相同，即

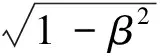
(8)

2.5理想气体功的相对论变换

按照气体功的定义并注意到理想气体压强的相对论变换式(6),可以得出

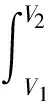
(9)

2.6理想气体热量的相对论变换

把功和内能的相对论变换式(8)和式(9)代入热力学第一定律可得

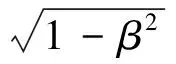
(10)

显然，热力学第一定律满足相对性原理.

2.7理想气体温度的相对论变换

温度和压强都是气体的状态参量，但温度不是力学量，它没有一个宏观确切的力学定义，套用上述方法时需要特别注意，比如不能想当然地认为理想气体的普适气体恒量R和波尔兹曼常数k与参照系的选择无关.从实验定律和统计解释两个方面来看，和温度有关的主要公式分别为

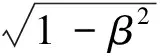
(11)

由于不能确定普适气体恒量是否与参照系的选择有关，我们将乘积作为一个整体看待.如果认为普适气体恒量R与参照系的选择无关，则有

R=R0

(12)

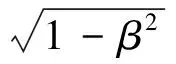
(13)

式(13)正是普朗克、 爱因斯坦和德布罗意的观点[2].

如果认为热力学温度与参照系的选择无关，那么普适气体恒量将按照式(13)的形式变化，即有

T=T0

(14)

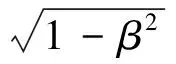
(15)

式(14)是Landsberg的观点[2].根据定义不难看出式(15)所表示的普适气体恒量的改变来源于气体体积的相对论变换.由于式(14)、(15)可以互为因果，由此得来的认定相对论温度变换关系式(14)反而显得说服力不足.

考虑到理想气体定容摩尔热容的表达式

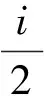
(16)

在式(16)中理想气体分子的自由度显然与参照系的选择无关.那么认为“气体体积的变化通过普适气体恒量的传递，进而引起分子摩尔热容的改变”的观点也难以使人信服.为此我们认为在都能给出同样作用的前提下，式(13)所给出的热力学温度的相对论变换更好一些.

2.8理想气体熵的相对论变换

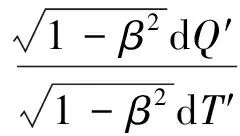
(17)

式(17)表明理性气体的熵也是个相对论不变量，相应的热力学第二定律也满足相对性原理.

3 结论

以上讨论给出了理想气体压强、体积、温度、内能、分子平均平动动能、热量、熵等常见热力学量的相对论变换.讨论还表明：考虑到普适气体恒量和摩尔热容的含义与表达式，普朗克、爱因斯坦、德布罗意等人给出的热力学温度的相对论变换式(13)更加合理.需要注意，在应用式(13)时，由于热力学温度数值本身都与参照系的选择有关，在计算热量时“温度变化1°”的概念也是相对的.

1 罗瑟.相对论导论.岳曾元，关德相，译.北京：科学出版社，1980.106～107,18～29

2 沈惠川.分析热力学的应用：平衡态热力学中温度的相对论变换.物理学报，2005，54(6)：2 482～2 488

TheRelativityTransformationinThermodynamics

Zhang Ying
(Susquehanna International Group, Philadelphia, PA19004, U.S.A.)

The paper presents the relativity transformation of the state parameters of ideal gas such as volume, pressure, internal energy, temperature, entropy etc. on the base of Lorentz transformation，and explains that the temperature relativity transformation provided by Plank, Einstein, de Broglie is more reasonable.

ideal gas; thermodynamics quantities; relativity transformation

2017-03-16)

张滢(1984- ),男，博士，数据分析师，主要从事计算机编程和数据分析工作.