基于全频带小波能量相对熵的脉冲涡流感应信号辨识
2017-09-25杨正理陈海霞
杨正理,陈海霞,徐 智
(三江学院机械与电气工程学院,江苏 南京 210012)
基于全频带小波能量相对熵的脉冲涡流感应信号辨识
杨正理,陈海霞,徐 智
(三江学院机械与电气工程学院,江苏 南京 210012)
脉冲涡流检测是一种新兴的无损检测技术,检测方便、成本低、安全性好,适用于对各种材料缺陷进行在线检测。然而,脉冲涡流感应信号强度微弱、识别困难,必须采用比较有效的信号处理方法对信号进行处理。为了提高脉冲涡流检测系统的精度和正确率,在详细分析了脉冲涡流感应信号特性后,提出了一种基于全频带小波能量相对熵的脉冲涡流感应信号辨识方法。对几种典型脉冲涡流感应信号的采样数据进行多尺度小波分解,并单支重构各尺度小波系数。利用小波变换对局部信号特征的放大作用以及小波相对熵对信号之间差异的辨识优势,计算各尺度小波能量占所有小波系数能量的权重系数,及原始信号在各频带下的小波能量相对熵,然后根据小波能量相对熵对脉冲涡流感应信号的类别进行信号辨识。理论分析和试验表明,该方法能够有效消除干扰,提高无损检测的精度和正确率。
小波能量相对熵; 脉冲涡流感应信号; 信号辨识; 无损检测; 小波变换; 多尺度分解
0 引言
脉冲涡流(pulsed eddy current,PEC)检测方法是一种新兴的无损探测技术,具有无需停机检测、成本低、安全性好等优点[1-3],从而被广泛应用于飞机结构、压力容器、核电站热交换管道等关键设备的缺陷检测中。脉冲涡流检测采用一定占空比的方波作为激励,通过对感应磁场分析来进行缺陷检测[4-5]。理论上,脉冲涡流感应信号比单频正弦涡流信号所获信息更多,因为脉冲涡流信号可提供某一范围内的连续多频激励[6-8]。通过检测脉冲涡流感应信号引起的磁场变化,许多学者分别在时域[9]、频域[10-11]以及时频域对磁场变化[12-13]进行分析,取得了一定成果。文献[14]以无试件时的检测信号或者无缺陷试件的检测信号作为参考信号,结合归一化技术减小检测系统对检测信号的影响,提高了缺陷分类的准确性。然而,脉冲涡流感应信号强度微弱,且检测信号易受传感器和检测系统的影响,并因含有多种噪声而使信号识别困难。目前,脉冲涡流感应信号辨识方法需进一步研究。
小波变换采用时域和频域的局部变换,能有效提取出信号在不同尺度下的信息,被誉为“数字显微镜”。常用的小波分析方法是对某一特定的分解尺度(对应某一特定范围频带)下的小波系数特征进行分析,从而得到原始信号的特征,并进行信号辨识。但由于系统参数和外部扰动的改变,信号特征信息并不一定正好集中在某一特定频带上,所以采用这种方法必然会丢失其他频带信息,不能考虑原始信号的所有特征,信号辨识结果也不一定准确。本文所用的方法考虑了原始信号所有频带信息,并结合小波变换对局部信号特征的放大作用以及小波相对熵对信号之间差异的辨识优势,使该方法的辨识精度得到很大提高。
本文采用上述方法对几种从试验装置得到的不同缺陷的典型信号进行辨识,介绍了基于全频带小波能量相对熵在脉冲涡流感应信号辨识中的应用。最后,通过大量的试验数据对该方法进行验证。
1 脉冲涡流无损检测装置
脉冲涡流无损检测装置由激励线圈和接收线圈组成。由信号发生器产生方波电流,经功率放大后加在激励线圈中,在电流的高电平段,被测试件中形成稳定的一次磁场[15-16];根据电磁感应原理,当电流跃变至低电平时,被测试件中将产生脉冲涡流感应信号。脉冲涡流感应信号在试件中产生二次磁场变化,由接收线圈转换为电压信号,这就是脉冲涡流感应信号[17-19]。
脉冲涡流无损检测装置结构如图1所示。
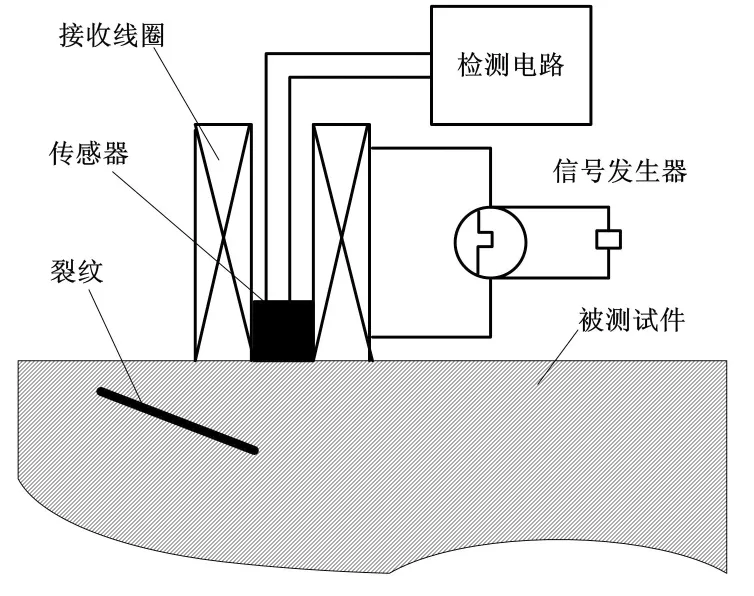
图1 检测装置结构图
检测电路接收采样脉冲涡流感应信号,将得到的数据进行滤波、分析和处理等操作,就能提取到缺陷特征。
采用图1所示的脉冲涡流检测装置,以采样频率fs=2 000 Hz对脉冲涡流感应信号进行采样,得到的各种缺陷的典型波形如图2所示。
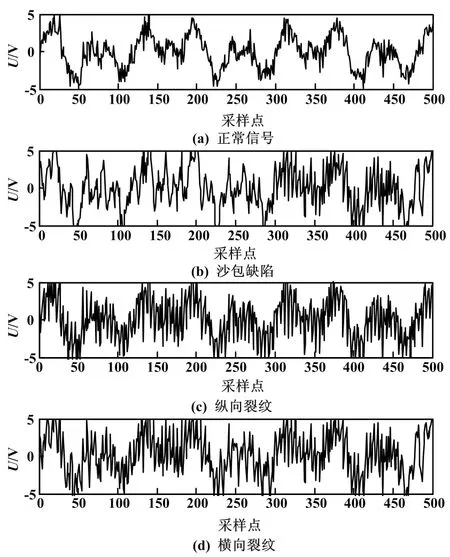
图2 各种缺陷的典型波形
从图2可以看出,这些信号波形包含了多种频率,并且含有强烈的白噪声,噪声几乎淹没了有用信号。当无损检测装置经过被测试件缺陷时,涡流感应信号会产生更为强烈的干扰信号,缺陷信号以高频形式与正常信号进行叠加。要对这些信号进行正确辨识,首先需要对采样的原始信号进行滤波,得到信噪比较高的去噪信号;再对滤波后信号进行分析、处理和辨识,区分缺陷类型。
2 全频带小波能量相对熵分析和定义
2.1 小波能量定义
设采样信号序列x(k),采用小波基对x(k)进行J尺度小波分解后,可以得到j(j=1,2,…,J,下同)尺度下k时刻低频逼近系数aj(k)和高频细节系数dj(k)。对分解结果进行一维小波单支重构,可以得到各尺度下小波系数集合AJ(k)和Dj(k)。原始信号x(k)可用小波系数集合表示:

(1)
为了便于描述,用DJ+1代替AJ(k),则式(1)又可表示为:
(2)
式中:Dj(k)为原始信号在j尺度下的小波系数集合。
当采样频率确定时,Dj(k)对应特定的频率范围。
(3)
式中:fs为原始信号的采样频率。
在相应频带下,Dj(k)包含着原始信号在该频带下的信号特征。因此,常来用作信号分析和辨识的特征子集。定义j尺度下k时刻的小波系数能量为:
(4)
根据叠加定理,有缺陷的脉冲涡流感应信号可分解为正常信号和缺陷信号。缺陷信号的频率和幅值与缺陷的类型有关,包含多种频率成分,信号特征十分丰富。当含有缺陷的原始信号经过小波变换后,缺陷信号的特征将根据缺陷类型的不同分布在不同频带的尺度上[20-25]。这也是基于频带能量进行信号辨识的理论基础。
2.2 小波基和分解尺度选择
小波变换所用的小波基不具有单一性,理论上有无数多种类型的小波基或变换核,能够满足不同的需要。但是必须根据具体问题选择合适的小波基,否则就难以达到满意的效果。而如何选择小波基还没有一个公认的统一原则。实际应用中,只能采用定性分析并结合试验比较的方法来选择合适的小波基。
小波分解尺度或层数的选取必须考虑信号中低频成分的影响和渗入。也就是说,小波分解的最大尺度主要应考虑频带划分特性,希望小波分解的最大尺度的低频逼近系数频带能够包含信号的主要能量。对本文信号进行分析处理时,当选择采样频率为2 kHz时,通过大量试验得知,选择分解尺度为5~6层比较合适,能够获得最佳的信号辨识效果。
图2中,4组采样数据中包含有大量的干扰噪声。在进行小波分解之前,采用小波阈值消噪法进行消除噪声处理,主要去除白噪声。消噪后信号能更准确体现原始信号的特征。
采用db10小波基对消噪后的4组采样数据进行5尺度小波分解,并对分解结果进行单支重构。典型信号的多尺度分解波形如图3所示。

图3 典型信号的多尺度分解波形图
图3中:A~D组波形分别对应图2中的正常信号、沙包缺陷、纵向裂纹、横向裂纹的分解结果;而1~6组波形分别对应第5尺度的低频逼近系数、第5、第4、第3、第2、第1尺度的高频细节系数。每一尺度的小波系数对应着一定的频带范围。第5尺度的低频逼近系数的频带范围为0~60.5 Hz;第5、第4、第3、第2、第1尺度下高频细节系数的频带范围分别为60.5~125 Hz、125~250 Hz、250~500 Hz、500~1 000 Hz、1 000~2 000 Hz。
比较图3的波形,正常信号的能量主要集中在第5尺度;而缺陷信号由于频率较高,其能量则主要分别集中在其他不同的尺度上。
信号经小波分解后,j尺度下的小波系数能量和为:
(5)
式中:S为采样数据组数,本文中S=4,下同;N为j尺度下小波系数的个数;Dij(k)为j尺度下的小波系数集合。
定义j尺度下,信号全频带的小波能量总和为:
(6)
由式(5)和式(6),定义j尺度下小波系数能量占全频带小波能量总和的比重,又称为频带权重系数:
pij=Eij/Ej
(7)
利用式(5)~式(7),计算图2中4个波形在各频带下的权重系数,并用柱状图表示,如图4所示。

图4 各频带下的权重系数图
2.3 小波相对能量熵定义
信息熵解决的是信息的定量描述问题,这是熵概念进一步泛化的基础。小波熵是小波分析理论和信息熵泛化定义相结合的产物,即将小波分解后的各尺度小波系数看作为一个信号源所发出的消息,所有小波系数可以看成是无序的、按一定概率进行分布的矩阵序列。用这些序列进行计算所得到的信息熵反映了这个矩阵的稀疏程度,也就是信号在各尺度下的概率分布的有序程度。由于这个信息熵和小波变换相结合,所以又称为小波熵。
不同类型的可辨识信号,其小波分解后各尺度的小波系数是不同的,因此可以在二维小波相空间上,基于不同的原理和分析方法,定义形式不同的小波熵测度,用以表征信号的特征。本文的小波能量相对熵就是基于该基本理论进行定义的。
但是,对于一些异常的信号,单纯的信息熵测度不能全面地反映信号的特殊性。正是由于小波分析技术的引入,将信息熵和小波技术相结合,利用小波分析对非平稳信号处理的局部化优点,充分体现信息熵对信号特征的表现能力,有效地分析异常信号。
根据上述关于小波能量的定义,结合小波熵理论,定义图2中各信号的小波分解在各尺度的小波相对熵Mij为:
(8)
小波相对熵表征了信号在各尺度下的概率分布散度,是对小波系数能量概率分布的一种量化方法,所以式(8)又称为小波能量相对熵。小波相对熵具有区别信号间微小差异的独特优势[23-24]。信号间差异越大,则相对熵越大;信号间差异越小,则相对熵越小。本文利用小波变换对信号的局部特征的放大作用,并结合小波相对熵对信号差异的优秀辨识能力,采用小波能量相对熵对脉冲涡流感应信号进行辨识分类,效果良好。
根据上述关于小波能量相对熵的定义,对图2中各波形进行小波分解,并计算各频带下的小波能量相对熵,构成4×6的小波能量相对熵矩阵,即:

(9)
3 信号辨识方法
根据小波能量相对熵矩阵可以看出,正常信号所含频率成分较低,所以它的能量主要集中在第5尺度上;当信号中含有沙包缺陷、纵向裂纹的缺陷信号时,这些缺陷信号包含了较正常信号频率高的信号频带,但因为这些缺陷信号频带比较集中,所以它们的小波系数能量主要集中在第4、第3尺度和第2、第1尺度上;横向缺陷信号的频率较正常信号高,但频带相对比较分散,所以其能量主要分布在第4、第3、第2、第1尺度上。信号辨识的算法流程如图5所示。
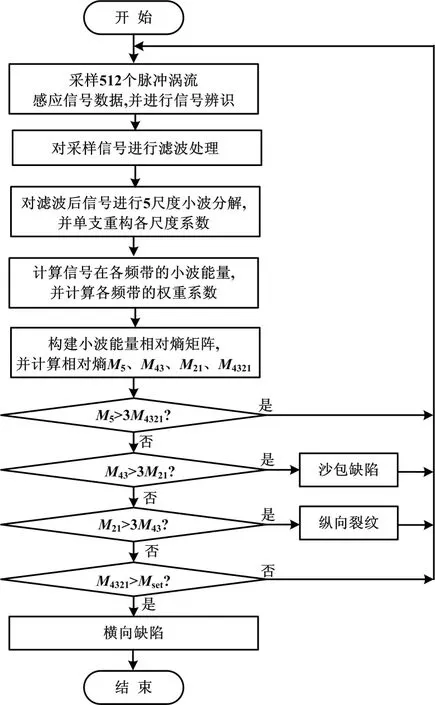
图5 信号辨识算法流程图
根据上面的分析,可以得到脉冲涡流感应信号的辨识依据:首先对采样信号进行小波阈值消噪,然后对消噪后信号利用db10小波基进行5尺度小波分解。根据对分解结构单支重构的小波系数,计算各频带下小波能量的权重系数,然后由权重系数构成小波能量相对熵矩阵。根据矩阵分别求取第5尺度,第4、第3尺度、第2、第1尺度,第4、第3、第2、第1尺度的综合小波能量相对熵M5、M43、M21、M4321。比较这些小波能量相对熵的大小,就能得到以下信号辨识依据。
①当M5>3M4321时,说明没有缺陷信号。
②当系统中有缺陷信号时,M43>3M21说明缺陷为沙包缺陷;M21>3M43说明缺陷为纵向裂纹。
③当系统中有缺陷信号时,当M4321>Mset时,说明缺陷为横向裂纹。Mset为整定值,设置其大小可用来确定脉冲涡流装置的检测灵敏度。
4 数字试验验证
通过在试验装置上随机放置测试件,然后采集脉冲涡流感应信号,并采用本文所述方法进行信号辨识(设置小波能量相对熵的整定值Mset=4.5)。本次试验的信号辨识结果正确率为100%。但系统在实际运行过程中,由于测试件及检测环境比试验环境复杂得多,辨识结果正确率没有本次试验过程中的辨识正确率高,但相比同类系统,采用本方法的辨识效果比较好。在实际运行过程中,往往只需要分辨出正常件和缺陷件,不需要再对缺陷件进行分类,所以辨识效果更好。从试验数据中任意选择20组信号辨识结果如表1所示,对信号进行辨识并对缺陷进行分类。表1中:分类正确率为100%。

表1 信号辨识结果
5 结束语
脉冲涡流感应信号经消噪处理并经小波多尺度分解后,各尺度上的能量分布特征不明显。利用小波变换对信号局部特征的放大作用,并结合小波能量相对熵对信号间差异的超强辨识能力,采用本文所述方法进行信号辨识,可以大大提高信号辨识的正确率。由理论分析和大量的试验结果得到以下结论。
①小波变换具有良好的局部化分辨能力,对信号特征有一定的放大作用。利用小波变换技术辨识脉冲涡流感应信号,可以对各种缺陷的微小差别进行辨识。
②该方法利用小波分解后的小波系数进行分析和处理信号,全面地利用了原始信号的所有特征。辨识结果更加精确和可靠。
③小波能量相对熵对信号间能量差异具有极强的辨识优势。利用该方法进行脉冲涡流感应信号辨识,加强了信号的特征,使缺陷信号辨识正确率得到了极大提高。
[1] 孙燕,董浩斌,葛健.基于涡流效应的齿轮毛坯件无损检测仪[J].自动化仪表,2015,36(8):98-102.
[2] 黄海鸿,汪燕,张曦,等.基于自旋阀GMR传感器的金属磁记忆检测[J].自动化仪表,2014,35(2):77-80.
[3] 郭锐,曹雷,贾娟,等.用于电力管道缺陷定量分析的涡流检测技术[J].自动化仪表,2016,37(5):4-9.
[4] ZHANG Y H,SUN H X,LUO F L,et al.Detection of a defect based on 3D magnetic field measurement for pulsed eddy current testing[J].Chinese Journal of Sensors and Actuators,2008,21(5):801-805.
[5] ADEWALE I D,TIAN G Y.Decoupling the influence of permeability and conductivity in pulsed eddy-current measurements[J].IEEE Transactions on Magnetics,2013,49(3):1119-1127.
[6] 武新军,黄琛,丁旭,等.钢腐蚀脉冲涡流检测系统的研制与应用[J].无损检测,2010,32(2):127-130.
[7] 陈兴乐,雷银照.导电导磁管道外任意放置线圈激励下脉冲涡流场时域解析解[J].物理学报,2014,63(24):20-29.
[8] 范孟豹,曹丙花,杨雪锋.脉冲涡流检测瞬态涡流场的时域解析模型[J].物理学报,2010,59(11):7570-7574.
[9] TETERVAK A,KRAUSE T W,MANDACHE C,et al.Analytical and numerical modeling of pulsed eddy current response to thin conducting plates[J].Review of Progress in Quantitative Nondestructive,2010,1211(1):353-360.
[10]张玉华,孙慧贤,罗飞路,等.基于三维磁场测量的脉冲涡流检测探头的设计[J].机械工程学报,2009,45(8):249-254.
[11]DESJARDINS D R,DRAUSE T W,CLAPHAM L.Transient response of a driver coil in transient eddy current testing[J].NDT&E International,2015,73(7):22-17.
[12]顾增涛,付跃文,薛盛龙.基于系统辨识的脉冲涡流信号提离效应[J].无损检测,2015,37(12):20-23.
[13]王健,滕永平,傅迎光,等.铁磁材料脉冲涡流厚度检测中的边缘效应[J].无损检测,2013(8):54-60.
[14]何一泽,罗飞路,胡祥超,等.矩形脉冲涡流传感器的三维磁场量与缺陷定量评估[J].仪器仪表学报,2010,31(2):347-351.
[15]HE Y Z,LUO F L,PAN M C,et al.Defect classification based on rectangular pulsed eddy current sensor in different directions[J].Sensor & Actuators A:Physical,2010,157(1):26-31.
[16]CHENG W,KOMURA I.Simulation for the assessment of wall thinning using eddy current method[J].Review of Progress in Quantitative Nondestructive,2011,1335(1):372-379.
[17]周德强,田贵云,王海涛,等.脉冲涡流技术在应力检测中的应用[J].仪器仪表学报,2010,31(7):1588-1593.
[18]徐志远,武新军,黄琛,等.有限厚铁磁性试件脉冲涡流响应研究[J].华中科技大学学报(自然科学版),2011,39(6):91-95.
[19]何正嘉,訾艳阳.Laplace小波及其工程应用[J].工程数学学报, 2001,18(1):87-92.
[20]訾艳阳,李庆祥,何正嘉.Laplace小波相关滤波法与冲击响应提取[J].振动工程学报,2003,16(1):67-70.
[19]徐志远,带包覆层管道壁厚减薄脉冲涡流检测理论与方法[D].武汉:华中科技大学,2012:31-33.
[20]刘金华,佘堃. 一种采用小波滤波的独立分量分析算法[J].电子测量与仪器学报,2010,24(1):39-44.
[21]LI Q,LI K C,CHEN X J.Research on lightning electromagnetic fields associated with first and subsequent return strokes based on Laplace wavelet[J]. Journal of Atmospheric and Solar-Terrestrial Physics,2013,93:1-10.
[22]何赟泽,罗飞路,胡祥超,等.矩形脉冲涡流传感器的三维磁场量与缺陷定量评估[J].仪器仪表学报,2010,31(2):109-113.
[23]尚赵伟,唐远炎,房斌,等.基于相对熵和复小波变换的纹理图像检索[J].重庆大学学报,2008,31(5):541-548 .
[24]何正友,刘志刚,钱清泉.小波熵理论及其在电力系统中应用的可行性探讨[J].电网技术,2004,28(21):17-21.
[25]冯旭哲,罗飞路,杨俊,等.基于小波支持向量机的数字通信信号调制识别[J].电子测量与仪器学报,2009,23(3):87-92.
RecognizingthePulsedEddyCurrentInductiveSignalBasedonFullWavebandRelativeEntropyofWaveletEnergy
YANG Zhengli,CHEN Haixia,XU Zhi
(School of Mechanical and Electrical Engineering,Sanjiang University,Nanjing 210012,China)
Pulsed-eddy current detection is a new type of nondestructive detection technology,which features convenient detection,low cost and safety,so it is suitable for various kinds of online detection of material defects.However,the intensity of pulsed-eddy current inductive signal is so weak that it is difficult to identify the signals,and more effective signal processing method must be adopted to deal with the weak signals.In order to improve the precision and accuracy of pulsed-eddy current testing system,the characteristics of pulsed-eddy current inductive signal are analyzed in detail,then a new identification method of pulsed-eddy current inductive signal based on the full waveband relative entropy of wavelet energy is proposed.The multi-scale wavelet decomposition is carried out for several typical sample data of the pulsed-eddy current inductive signals,and the wavelet coefficient of each scale is reconstructed.By using the amplification function of wavelet transform to local signal characteristics and the identification superior of wavelet relative entropy to the difference among signals,the weight coefficients of each scale wavelet energy in all the wavelet coefficient energy are calculated,and each signal wavelet energy relative entropy in each frequency band is calculated,then according to these characteristics of wavelet energy relative entropy,the category of pulsed-eddy current inductive signal is identified.Theoretical analysis and experimental results show that such method effectively avoids disturbance,and improves the precision and accuracy of nondestructive detection.
Wavelet energy relative entropy; Pulsed eddy current inductive signal; Signal recognition; Nondestructive detection; Wavelet transform; Multi-scale decomposition
TH-39;TP73
: A
10.16086/j.cnki.issn1000-0380.201709018
修改稿收到日期:2017-03-27
杨正理(1971—),男,硕士,副教授,主要从事金属材料无损检测方向的研究。E-mail:zhengli-yang@163.com。
