基于Backstepping的自适应模糊控制算法研究
2017-09-25王泰华王坤非姚学召
王泰华,王坤非,姚学召
(河南理工大学电气工程与自动化学院,河南 焦作 454000)
基于Backstepping的自适应模糊控制算法研究
王泰华,王坤非,姚学召
(河南理工大学电气工程与自动化学院,河南 焦作 454000)
机器人是一种不确定性、非线性系统,为了实现不确定机器人系统的精确控制,基于Backstepping的自适应模糊控制算法,对直驱电机双关节机械臂进行了研究。首先,针对直驱技术双关节机械臂的数学模型,并结合Backstepping算法,对该系统进行相关数学理论分析;其次,详细介绍了Backstepping自适应模糊控制器的设计过程,并通过Lyapunov函数证明所设计控制系统闭环有界,且稳定可靠;最后,以Matlab软件组建该控制算法仿真平台,通过试验结果与单一自适应模糊控制算法比较分析表明,所设计控制器对关节1和关节2的位置跟踪响应时间大约分别为0.12 s和0.1 s,而且位置跟踪曲线更加精确。因此,该智能控制算法可以实现对不确定机器人系统位置的精确跟踪和快速响应,为解决高精度设备的轨迹跟踪问题提供了一定思路。所提出的直驱机械臂既节省资金,又具有很高的实用价值,值得推广和应用。
Backstepping; 机器人; 电机; 自适应模糊控制; 位置跟踪
0 引言
针对现阶段我国机器人行业缺乏核心技术及关键零部件问题,王延觉等人[1-2]提出直驱力矩电机替代传统“电动机+减速器”伺服系统[3]。事实上,由传统驱动方式变为直驱后,对软件(特别是控制算法)提出了更高的要求。文献[4-5]运用人工神经网络设计控制器,来解决机器人操纵器反向运动学的问题。文献[6]设计了一种标称计算力矩控制器附加自适应模糊补偿控制器,取得了良好的期望跟踪轨迹。文献[7-8]采用基于Backstepping的方法,针对不同的机器人进行控制器设计,验证了控制算法的可行性。为此,本文以直驱技术双关节机械臂为对象,设计Backstepping自适应模糊控制算法,实现对不确定机器人系统的位置期望跟踪及精确控制。
1 系统描述
直驱技术刚性双关节机械臂示意图如图1所示。

图1 双关节机械臂示意图
其动态方程可表示为[9]:
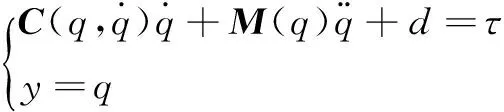
(1)
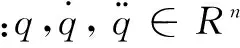
若系统的参数是未知且有界的,则由式(1)可知,该机械臂具有以下特性。
①M(q)是正定对称矩阵,且有界,即存在0<σ0 ②惯性矩阵M(q)、向心力和哥氏力矩阵C(q,q)具有以下关系: q[M(q)-2C(q,q)]=0 (2) 为了便于采用Backstepping方法,首先定义x1=q,x2=q,则式(1)变为: (3) 式中:M-1(x1)和C(x1,x2)均为未知非线性光滑函数。 2.1 控制器设计 为了进行Backstepping控制器的设计,本文先进行如下工作。 步骤1:定义变量公式。 假设yd为期望角度,且具有二阶导函数。控制目标为y跟踪指令轨迹yd。误差定义为: (4) 式中:α1为x2的估计值。 通过对α1的选取,使得z2趋近于0。 则由式(3)和式(4)得: z1=x2+α1-yd (5) (6) 如果z2=0,则第一个子系统稳定。 步骤 2:控制律设计。 由式(3)和式(4)得: z2=x2-α1=M-1τ-M-1Cx2-M-1d-α1 (7) 取控制律为: τ=-λ2z2-z1-φ (8) (9) 式中:f=-Cα1-Mα1。 将控制律式(8)代入式(9),得: (10) 由f表达式可知,其包含了该直驱技术双关节机械臂的建模信息。而为了实现无模型信息的控制,运用模糊系统的方法[9-11]逼近f。假设引入φ来逼近非线性函数f的模糊系统,采用单值模糊化、乘积推理机和重心平均反模糊化。此外,针对f的模糊逼近,这里可以采用分别逼近f(1)和f(2)的形式,则该模糊系统可设计为: (11) (12) 2.2 稳定性分析 对整个系统,取Lyapunov函数为: (13) 式中:γ>0。 对式(13)求导得: (14) 将自适应控制律式(12)代入式(14)可得: (15) 因为(θ-θ*)T(θ-θ*)≥0,则2θ*Tθ-2θTθ≤-θTθ+θ*Tθ*,所以式(15)可变为: (16) 由(θ*+θ)T(θ*+θ)≥0可知,-θ*Tθ-θTθ*≤θ*Tθ*+θTθ,则: 即: (17) 取λ2>1,由式(17)和系统特性不等式M≤σ0I得: (18) (19) 因为外界扰动d∈Rn有界,则存在D>0,满足dTd≤D,则: (20) (21) 为验证该控制算法的有效性以及先进性,取该控制对象为双关节机械臂模型,其动态方程如式(1)所示,并在Matlab/Simulink环境下进行仿真试验[12],最终对试验结果与自适应模糊控制算法进行比较,证明该算法设计合理、控制效果明显。 取系统参数:M1=2,M2=1,L1=1,L2=1,R1=0.5,R2=0.5。M1和M2分别为第一和第二连杆质量,L1和L2依次为第一和第二连杆长度,R1和R2分别是第一和第二连杆一次到相应其连杆重心距离。系统的初始状态为x(0)=[1 1 0 0]T。外界扰动为d=[0.25sint0.25sint]T。 同时,控制系统相关参数设计如下:λ1=10,λ2=15,k=1.5,γ=2,λ1=2;λ2=2.5,k=1.5;γ=2期望轨迹为yd=sin(2πt)。 模糊系统式(11)的隶属函数为: (22) 式中:i=1,2,3,4。 利用MATLAB仿真,基于Backstepping的位置跟踪和单一自适应模糊控制的位置跟踪如图2、图3所示。 图2 基于Backstepping的位置跟踪图 图3 单一自适应模糊控制的位置跟踪图 分析图2、图3可知,两种控制算法均可以实现对位置期望的跟踪,但基于Backstepping的自适应模糊控制响应更为快速,其对关节1和2的位置跟踪在系统刚开始工作时就迅速作出响应,关节1需要约0.12 s,关节2需要约0.1 s,并且所设计的控制器跟踪曲线更为圆滑;而自适应模糊控制下的关节1的响应时间大约需要0.8 s、关节2需要0.35 s左右,控制效果也没有本文所采用的算法精度高。可见,本文所设计的控制器控制效果良好,可以实现对不确定性机器人系统的精确控制。 本文以现在热门的直驱技术为背景,查阅相关文献,证明直驱力矩电机可以替代传统的“电动机+减速器”伺服系统,这为我国机器人产业的创新发展提供了参考建议。另外,本文以直驱技术机械臂为研究对象,分别进行了基于Backstepping的自适应模糊控制算法和自适应模糊控制算法研究,主要得到以下结论。 ①通过对直驱力矩电机的相关研究得到,该技术在工业机器人拥有广阔的应用前景,其中直驱力矩电机是取代减速器、增加机器人产业值以及带动机器人产业创新的理想器件。 ②依据稳定性证明可知,本文所设计的控制算法合理且稳定可靠,适合该类系统的相关研究。 ③通过将该控制算法与单一自适应模糊控制分别进行仿真和比较可知:本文所设计的基于Backstepping的自适应模糊控制算法具有更快的响应速度、更优秀的位置跟踪控制能力。 [1] 王延觉,杨凯.低速大力矩直接驱动电动机研究与应用进展[J].微特电机,2007(5):46-49. [2] 贾帅.工业机器人直接驱动技术研究[D].太原:中北大学,2015. [3] 杜品圣.回归“工业4.0”的本源,驶向智能制造的快车道[J].自动化仪表,2016,37(6):1-7. [4] NANDA SK,PANDA S,SUBUDHI P R S,et al.A novel application of artificial neural network for the solution of inverse kinematics controls of robotic manipulators[J].International Journal of Intelligent Systems and Applications(IJISA),2012,4(9):81-91. [5] JHA P,BISWAL B B,SAHU O P.Intelligent computation of inverse kinematics of a 5-dof manipulator using MLPNN[M].Heidelberg:Springer International Publishing,2014. [6] 梁捷,陈力.空间机械臂关节运动的自适应模糊补偿控制[J].系统仿真学报,2011,23(3):577-582. [7] 徐传忠,王永初,杨冠鲁.多关节机器人的反演自适应模糊滑模控制[J].电气自动化,2011,33(2):28-31. [8] 张晓霞.基于Backstepping的几类机器人控制研究[D].秦皇岛:燕山大学,2012. [9] 刘金琨.机器人控制系统的设计与MATLAB仿真[M].北京:清华大学出版社,2008. [10]张叶茂,杨晓武.自适应模糊PID在压铸机控制系统中的应用[J].热加工工艺,2016(23):96-99. [11]王蕊,李宏光.基于FRI-FCM的工业过程模糊监控[J].自动化仪表,2016,37(7):21-26. [12]王坤非,王泰华,姚学召,等.基于MATLAB/Simulink FIR数字滤波器设计的不同实现方法研究[J].电子测量技术,2017,40(1):17-20. StudyontheAdaptiveFuzzyControlAlgorithmBasedonBackstepping WANG Taihua,WANG Kunfei,YAO Xuezhao (School of Electrical Engineering and Automation,Henan Polytechnic University,Jiaozuo 454000,China) The robot is an uncertain and nonlinear system.In order to realize the precise control of the uncertain robot system,with the dual-joint manipulator which is composed of the direct drive motor as the object,the self-adaptive fuzzy control algorithm based on backstepping is studied.Firstly,in accordance with the mathematical model of the direct drive double-joint manipulator,and combining with the basis of backstepping algorithm,the relevant mathematical theory is analyzed.Secondly,the design process of backstepping adaptive fuzzy controller is introduced in detail,and relying on Lyapunov function,to prove that the designed control system is closed - loop bounded and stable and reliable.Finally,the simulation platform is established by Matlab software.The comparison between the experimental results and the single adaptive fuzzy control algorithm shows that the designed controller has about 0.12 s and 0.1 s respectively for the positional tracking response for joint 1 and joint 2,and the position tracking curve is more accurate.Therefore,this intelligent control algorithm can implement accurate tracking and fast response to the position of the uncertain robot system,and it provides a certain idea for solving the tracking of high precision equipment,and the proposed direct drive manipulator both saves money and provides high practical value,which is worth to be promoted and applied. Backstepping; Robot; Electric motor; Adaptive fuzzy control; Position tracking TP241; TH113.2 : A 10.16086/j.cnki.issn1000-0380.201709009 修改稿收到日期:2017-04-21 王泰华(1976—),男,硕士,副教授,主要从事工业过程控制及工矿自动化方向的研究。E-mail:taihua@hpu.edu.cn。 王坤非(通信作者),男,在读硕士研究生,主要从事工业过程控制、机器人智能控制方向的研究。E-mail:wkfzyx@163.com。2 控制器设计及稳定性分析

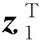

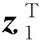







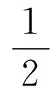
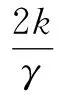
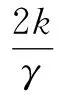


3 系统整体仿真试验


4 结束语
