利用滑动式Lagrange插值方法拟合卫星精密星历
2017-09-23郭忠臣
郭忠臣
宿州学院环境与测绘工程学院,宿州,234000
利用滑动式Lagrange插值方法拟合卫星精密星历
郭忠臣
宿州学院环境与测绘工程学院,宿州,234000
为了得到精确的卫星三维坐标,应用滑动式Lagrange插值方法对GPS精密星历内插,给出卫星位置插值公式。通过设置不同的插值阶数,对插值精度统计分析。结果表明:插值精度随着阶数的增加而提高,当阶数达到11阶时,插值精度较高,X、Y和Z三个方向的RMS分别达到0.378、0.514、0.306 mm,且均值偏差都在0.1 mm左右,精度略优于其他阶数,可满足导航方面的需求。
滑动式Lagrange;插值;精密星历;GPS
在高精度卫星导航和深空探测等领域中,需使用精确的卫星三维坐标。当前使用较多的为IGS(International GNSS Service)发布的精密星历产品,但精密星历是按照一定时间间隔提供的[1-2],若想得到任意时刻的卫星位置,必须对精密星历进行拟合和插值。本文采用滑动式Lagrange插值算法对IGS提供的精密星历进行处理,并对插值结果进行统计分析,为后续研究提供参考。
1 滑动式Lagrange插值算法原理
利用Lagrange多项式可内插出节点之内任意时刻的卫星位置。Lagrange插值函数可表示为[3-5]:
(1)
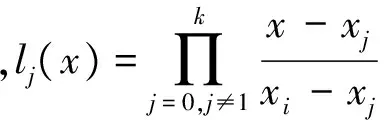
滑动式Lagrange插值算法是在原有方法的基础上构建一个活动的“窗口”,以保证插值点的位置时刻保持在插值范围的中心。当选取的节点数为奇数时,最佳插值点有2个,选取的节点数为偶数时,最佳插值点即为中间时刻。如选取9个节点时,可构造8阶Lagrange拟合多项式,此时最佳插值点位于第4至第5和第5至第6个节点之间;选取8个节点时,可构造7阶Lagrange拟合多项式,此时最佳插值点位于第4和第5个节点之间,具体说明见图1。

图1 滑动式Lagrange插值示意图
根据IGS发布的精密星历可得到各给定时刻卫星的三维坐标X(t),本文选取偶数个节点作为插值点[3],依据上述原理,可得任意时刻t的卫星位置的表达式为[6]:
(2)
其中,X(t)、X(ti)为对应时刻t和ti的位置,i,j≠0,2n-1为插值阶数。
2 实验分析
本文采用WHU站提供的时间间隔为15 min、包含卫星坐标和钟差的1 791周(GPST)的精密星历数据,共672组三维坐标,提取该周内以1 800 s为时间间隔(0 s,1 800 s,3 600 s,5 400 s,7 200 s,…,604 800 s)的坐标作为已知数据,对本周内26 100~578 700 s之间每隔1 800 s的时刻位置进行插值拟合。选取PG04号卫星进行Lagrange插值计算,并对插值结果进行统计分析。
表1和图2列出了使用不同阶数的Lagrange插值精度的统计结果,通过分析可知:(1)随着阶数的增加,插值精度明显提高,但当阶数增加到一定程度时,精度趋于稳定;(2)当阶数增加到11阶后,插值精度较高,X、Y和Z三个方向的RMS分别达到0.378、0.514、0.306 mm,且均值偏差都在0.1 mm左右,精度略优于其他阶数;(3)随着阶数增加,插值过程中的计算量增加,对计算机的耗损增加,当需要大量插值结果时,可从精度与耗时等方面综合考虑,以确定最佳阶数。
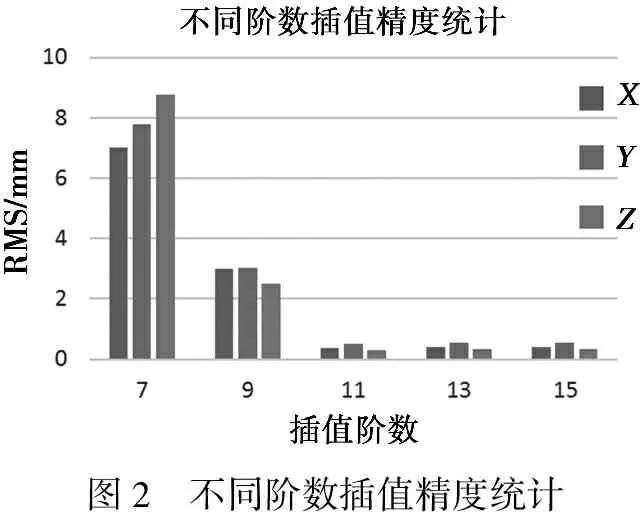
图2 不同阶数插值精度统计
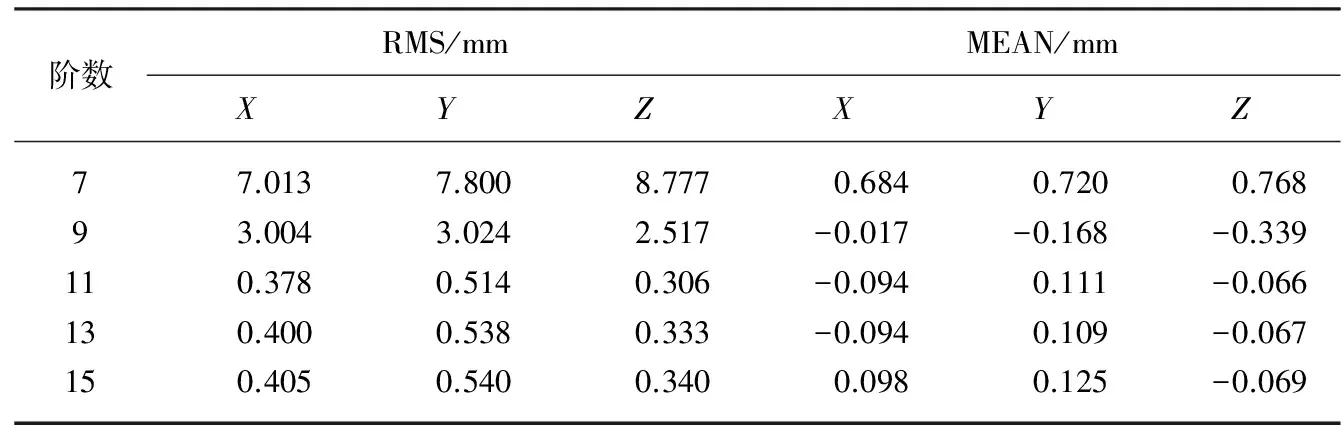
表1 不同阶数插值精度统计
表2列出了部分时刻的精密星历和当阶数为11阶时的插值结果,表3给出了相应时刻的插值误差。由表3可知,当阶数为11阶时,X、Y和Z三个方向的插值误差均优于1 mm,能满足导航方面的需求。
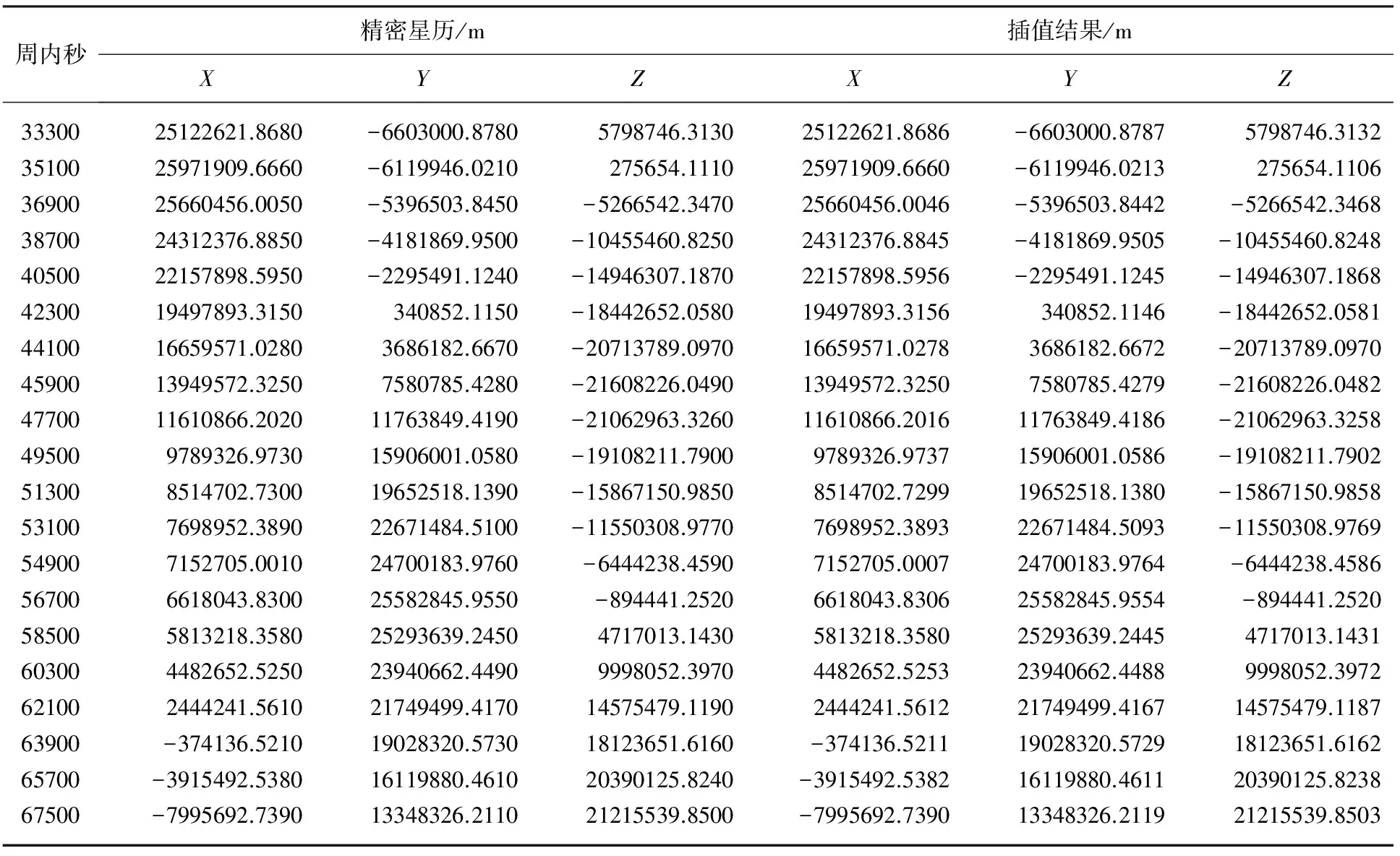
表2 部分时刻的精密星历与插值结果
4 结束语
(1)滑动式Lagrange插值算法因算法简单、插值精度高而广泛应用于各个领域,用它对精密星历插值,可使插值误差保持在1 mm以内,基本满足导航方面的需求。
(2)本文选取不同阶数进行插值,插值精度随着阶数的增加而增加,但当阶数增加到一定程度时,插值精度趋于稳定,甚至会低于低阶的插值精度。
(3)文中选取了一周的精密星历进行插值计算,但若想对该周的起始与结束时刻进行插值,需联合使用前一周和后一周数据。
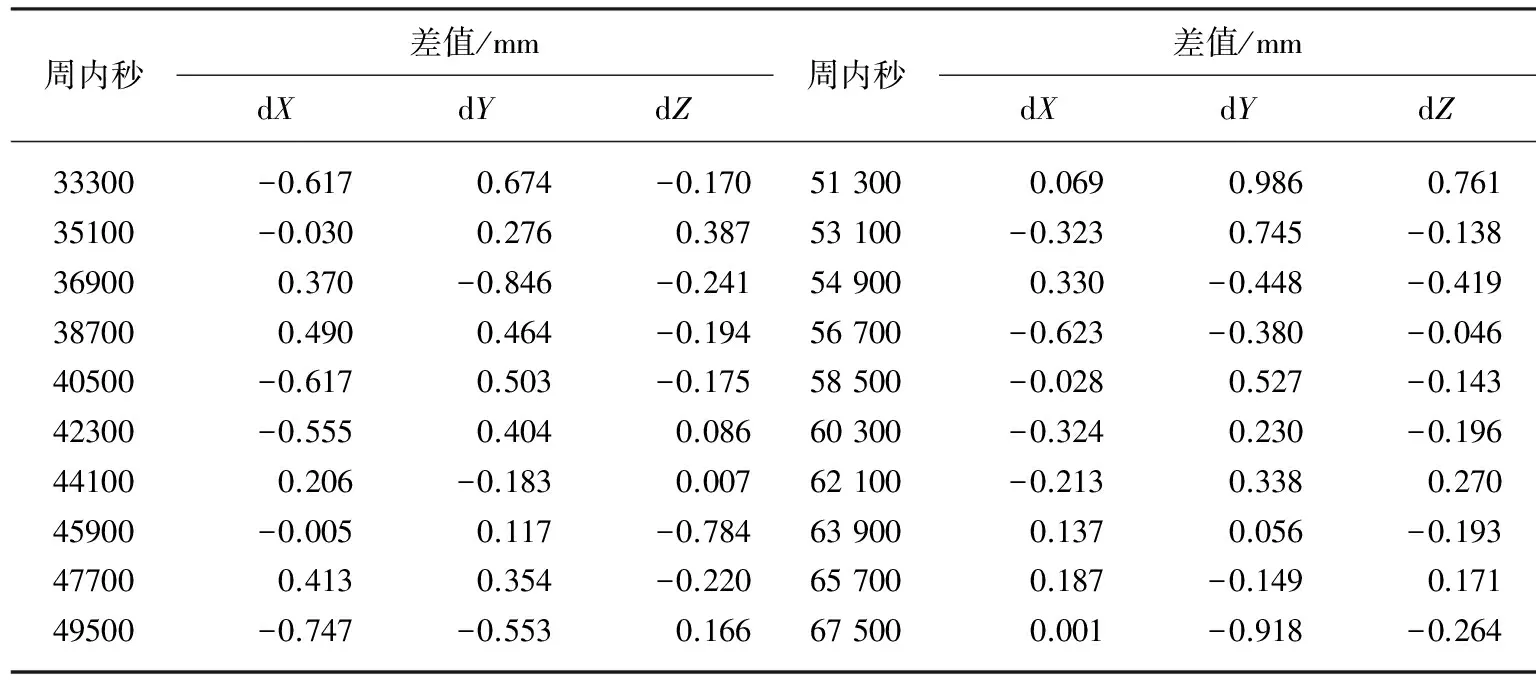
表3 部分时刻插值误差
[1]王兴,高井祥,王坚,等.利用滑动式切比雪夫多项式拟合卫星精密坐标和钟差[J].测绘通报,2015(5):6-8
[2]何玉晶,杨力.基于拉格朗日插值方法的GPSIGS精密星历插值分析[J].测绘工程,2011,20(5):60-62
[3]雷雨,赵丹宁,高玉平,等.基于滑动式Lagrange插值方法的GPS精密星历内插分析[J].测绘工程,2013,22(2):34-36
[4]向荣荣,兰孝奇,刘锋,等.拉格朗日和切比雪夫多项式在精密星历插值中的应用[J].测绘与空间地理信息,2015,38(11):131-134
[5]何玉晶,杨力.基于拉格朗日插值方法的GPSIGS精密星历插值分析[J].测绘工程,2011,20(5):60-62
[6]郭忠臣,高井祥,曹新运.北斗广播星历轨道及钟差精度分析[J].煤炭技术,2015,34(7):113-116
(责任编辑:汪材印)
P228.4
:A
:1673-2006(2017)07-0106-03
10.3969/j.issn.1673-2006.2017.07.027
2017-03-09
郭忠臣(1992-),安徽阜阳人,硕士,助教,研究方向:GNSS数据处理。
