基于迭代指导滤波的立体匹配方法

李金凤 边继龙

1(牡丹江师范学院计算机与信息技术学院 黑龙江 牡丹江 157011)2(东北林业大学计算机与信息工程学院 黑龙江 哈尔滨 150040)

基于迭代指导滤波的立体匹配方法

李金凤1边继龙2

1(牡丹江师范学院计算机与信息技术学院 黑龙江 牡丹江 157011)2(东北林业大学计算机与信息工程学院 黑龙江 哈尔滨 150040)

针对立体匹配当中的匹配精度问题，提出一种基于迭代指导滤波的立体匹配方法。该方法首先利用自适应窗口方法根据图像的灰度变化自适应地选择支撑窗口，再根据指导滤波累积原始匹配成本，并采用“胜者全取”方法计算视差，然后利用计算视差对匹配成本进行修正，进行再次累积并计算视差，最后反复迭代这一过程直到达到最大的迭代次数为止。实验结果表明，该方法可以获得较高精度的视差图，而且对立体像对中的不连续区域具有较强的鲁棒性。

立体匹配 自适应窗口 指导滤波 自适应权重

0 引 言

立体匹配是计算机视觉领域中的一个热点问题，它利用同一场景的两幅或者多幅图像抽取场景的三维信息。到目前为止，已经提出大量立体匹配方法[1]解决立体对应问题，这些立体匹配方法根据视差选择方式不同可大致分为：局部立体匹配方法和全局立体匹配方法。局部立体匹配方法[2-7]是利用“胜者全取”方法选择视差，而全局立体匹配方法[8]则是通过优化算法选择视差。这些立体匹配方法最终都是通过最小化匹配成本选择视差，因此定义和计算匹配成本是局部及全局立体匹配方法的关键所在。匹配成本的好坏直接影响立体匹配方法的匹配精度，其一般计算方法是通过在一个预定义支撑区域内累积原始匹配成本即成本累积。成本累积主要包含两类：一类是基于自适应窗口的成本累积方法，另一类是基于自适应权重的成本累积方法。基于自适应窗口成本累积方法的主要原理是为每一点选择一个合适的支撑窗口，尽量保证窗口内所有像素点的视差都等于待匹配点的视差，即保证支撑窗口内的局部场景符合“前视平坦”假设。如果当支撑窗口内像素点的视差存在较大变化时，则会导致立体匹配方法产生边界膨胀现象。这种现象多发生在物体边界处，这是因为在物体边界处的支撑窗口经常包含了不同视差。基于自适应权重成本累积方法的主要思想是根据指导图像为支撑窗口内的像素点计算权重信息，然后根据其相应的权重信息累积原始匹配成本。该方法具有较高的匹配精度，其精度接近于全局立体匹配方法，但该方法的时间复杂度过高。

Yoon[3]等在2006年提出一种基于自适应权重的立体匹配方法，该方法利用双边滤波累积原始匹配成本，然后通过“胜者全取”方法计算视差值。该方法可以获得高精度的视差图，但是该方法的时间复杂度较高，之后人们陆续提出一些改进措施降低了该方法的时间复杂度。由于基于自适应权重的立体匹配方法具有较高的匹配精度，因此该类方法已成为当前立体匹配研究领域中的一个热点问题。He Kaiming[4]在2010年提出一种指导图像滤波，该方法根据指导图像内容计算滤波输出。指导滤波是一种边保护滤波，它类似于双边滤波。但该方法在边缘附近有更好的效果，而且该方法接近于线性时间复杂度，独立于滤波核大小。Hosni[5]等在2011年利用He Kaiming提出的指导滤波设计一种基于指导滤波的立体匹配方法，该方法的立体匹配效果优于Yoon等提出的基于自适应权重的立体匹配方法。但是由于该方法利用指导滤波计算匹配成本时采用的是固定窗口，因此该方法在物体边界处发生膨胀现象。

为解决基于指导滤波的成本累积方法在物体边界处产生膨胀问题，同时为增强匹配成本的鲁棒性以提高立体匹配精度，本文提出一种基于迭代指导滤波的立体匹配方法，该方法主要有以下两点贡献：首先提出一种自适应窗口方法以解决支撑窗口跨越边界导致视差图在物体边界处产生膨胀问题；其次为增强匹配成本的鲁棒性，提出一种基于指导滤波的迭代成本累积方法。

1 基本理论

Hosni等利用He Kaiming提出的指导滤波设计一种基于指导滤波的立体匹配方法，该方法的匹配精度优于其它局部立体匹配方法。指导滤波的主要思想：假设滤波输出q与指导图像I在局部范围内符合线性模型，其线性模型表达式为：

qi=akIi+bk∀i∈Nk

(1)

式中，ak、bk分别表示线性系数，Nk表示以像素点k为中心的局部窗口。现假定在局部窗口Nk内，滤波输入p和滤波输出q满足如下关系：

qi=pi-ni

(2)

式中，n表示高斯噪声。由于局部窗口内的所有像素点都满足式(2)，因此可以为每个局部窗口建立如下形式的成本函数：

(3)

式中，ε表示规范常量。为求解线性系数ak和bk，利用最小二乘法对成本函数式(3)最小化得：

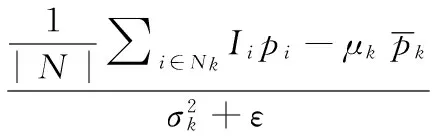
(4)

(5)

如果将式(1)的线性模型应用到整幅图像，则每个像素点i获得|N|个不同的滤波输出。这是因为在图像空间中，有|N|个不同的局部窗口包含像素点i，这些局部窗口将分别产生不同的滤波输出。为给每一像素点i确定唯一一个滤波输出值，比较简单有效的方式是对这些滤波输出求平均，由此可得：

(6)

由于矩形支撑窗口具有对称性：

(7)

因此，式(6)可以简化为：

(8)

在基于指导滤波的立体匹配中，就是利用式(8)对原始匹配成本进行累积。在计算累积成本时，其指导滤波的输入p为视差空间图中的每一视差d所对应的二维成本矩阵c(:,d)即视差空间图按d维切割的二维数组，指导图像I为参考图像IL，像素点i的累积成本C(i,d)可表示为：

(9)

2 算法实现及关键步骤

本文提出一种基于迭代指导滤波的立体匹配方法。该方法首先提出一种自适应窗口方法以解决局部立体匹配当中的边界膨胀问题，然后提出一种基于迭代指导滤波的成本累积方法以提高匹配成本对噪声的鲁棒性，确保匹配成本能准确地反映匹配约束。

2.1 自适应窗口

在此，本文首先分析指导滤波特点，然后结合立体匹配当中成本累积的要求，提出一种基于自适应窗口的指导滤波方法累积匹配成本。为了方便分析指导滤波的行为，本文假设指导图像I恒等于滤波输入p。在这种情况下，式(4)中的ak和bk简化为：

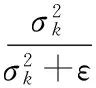
bk=1-akμk

(10)

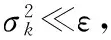
(11)

式中，φ(k)表示像素点k的最优支撑窗口大小，λ表示预定义灰度变化阈值。根据指导图像的灰度变化自适应地为每一待匹配点确定支撑窗口大小，在弱纹理区域选择较大的支撑窗口，而在纹理区域选择较小的支撑窗口。

2.2 迭代指导滤波

本文利用计算视差图提供的先验信息，提出一种迭代指导滤波方法来增加立体匹配的准确率。该方法的主要思想是利用计算视差图修正匹配代价，然后利用指导滤波再次累积匹配成本，计算视差并反复迭代，直到达到给定的最大迭代次数为止。其匹配代价修正表达式为：

(12)

式中，Dmax表示最大视差范围，d(p)表示像素点p的计算视差。

2.3 算法实现

基于迭代指导滤波的立体匹配方法首先根据灰度信息及灰度梯度信息计算匹配成本，再根据指导图像的灰度变化选择支撑窗口，并通过指导滤波累积匹配成本，然后利用“胜者全取”策略计算视差，最后利用计算视差修正原始匹配成本并用指导滤波再次累积匹配成本计算视差，反复迭代此步直到达到指定的迭代次数为止。其算法的主要步骤如下：

(1) 计算原始匹配成本。根据视差范围及左右图像的灰度信息及梯度信息计算原始匹配成本，构成一个三维视差空间图c(p,d)，其计算公式如下：

c(p,d)=α·min(‖IL(p)-IR(p-d)‖,τ1)+ (1-α)·min(‖▽xIL(p)-▽xIR(p-d)i‖,τ2)

(13)

式中，IL表示参考图像，IR表示匹配图像，α(≤1)表示权重比，d表示视差，▽x(·)表示函数在x方向的梯度变化，τ1和τ2分别表示灰度和梯度截断阈值。

(2) 根据式(11)每一待匹配点确定支撑窗口大小。

(3) 根据支撑窗口大小φ(k)，利用指导滤波累积原始匹配成本。

(4) 根据“胜者全取”方法计算视差：

(14)

(5) 根据式(12)修正原始匹配成本，然后转到步骤(3)，直到达到给定的最大迭代次数为止。

3 实验结果与分析

3.1 实验环境

该实验利用C++实现了本文提出的立体匹配方法，其运行环境为联想erazer笔记本电脑，其配置为双核CPU 2.60 GHz，4 GB内存，64位win7操作系统。实验采用了Middlebury网站提供的Tsukuba、Venus、Teddy和Cones对本文算法进行了验证。

3.2 参数分析

本文提出的立体匹配方法涉及了一些参数的选择，这些参数包括利用式(13)计算原始匹配成本时参数τ1、τ2及α；利用式(11)进行窗口选择参数λ以及迭代次数。这些参数在一定程度上会影响匹配精度，为了获得较高精度的匹配，该部分利用了Middlebury网站提供的Tsukuba图像对这些参数进行了分析，为本文方法选择一组最优参数值。

实验1首先给定一组参数τ1、τ2、α及迭代次数数值，然后通过改变窗口选择参数λ来分析它对匹配精度的影响。本组实验τ1、τ2、α及迭代次数分别为：0.027 5、0.078、0.1、10，其测试结果如图1所示。通过图1，我们可以看出λ=2.1时匹配效果最好。当λ≥2.5时，匹配精度趋于收敛，这是因为当灰度阈值λ大于该阈值时，自适应窗口策略退化为固定窗口。

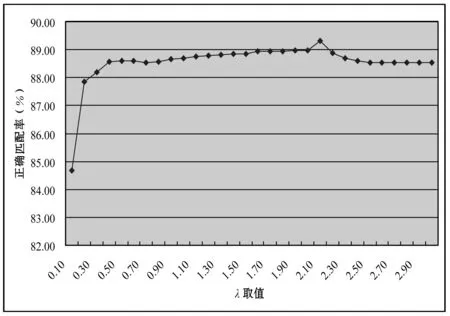
图1 窗口选择参数λ分析

实验2本实验分析了权重参数α对匹配精度的影响。本文方法在计算原始匹配成本时同时考虑了灰度成本和梯度成本。权重参数α调整他们各自对原始匹配成本的贡献量，因此α的取值在[0 ,1]范围之间。在α为0时，原始匹配成本仅由梯度成本构成；在α为1时，原始匹配成本由仅有灰度成本构成。本组实验τ1、τ2、λ及迭代次数参数值分别选择为：0.027 5、0.078、2.1、10，然后改变调整参数α观察对匹配精度的影响，其测试结果如图2所示。通过图2，我们可以看出当权重参数α为0.2时匹配精度达到最优。当随着α逐渐接近于1时，梯度匹配成本所占比例不断降低，匹配精度也随之下降，这表明了在原始匹配成本当中引入适量的梯度成本可以有利于提高匹配精度。

图2 权重参数α分析

实验3本实验分析灰度截断阈值τ1对匹配精度的影响。本组实验τ2、λ、迭代次数及α参数值分别选择为： 0.078、2.1、10、0.2，然后调整参数τ1观察对匹配精度的影响，其测试结果如图3所示。通过图3，我们可以看出当τ1等于0.35时，匹配精度达到最优。通常在立体匹配当中，假定同一场景点在不同像平面上的像点具有相似的灰度值。但是在实际当中，由于成像时物理环境差异导致某些对应点具有较大的灰度差，这导致立体匹配方法误认为错误匹配。通过截断阈值的思想在一定程度上可以减少这方面对匹配精度的影响，也有一些学者[9-10]提出了一些其他方法来解决立体匹配当中的辐射差异。

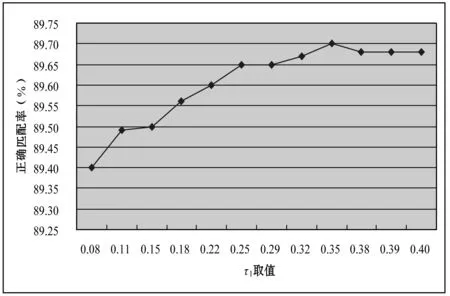
图3 灰度截断阈值τ1分析

实验4本实验分析了梯度截断阈值τ2对匹配精度的影响。首先给定τ1、λ、迭代次数及α的参数值：0.35、2.1、10、0.2，然后调整梯度截断阈值τ2观察对匹配精度的影响，其结果如图4所示。通过图4可以看出，当τ2等于0.078时，匹配精度达到最优。

图4 梯度截断阈值τ2分析

实验5本实验分析了迭代次数对匹配精度的影响。本实验参数τ1、λ、迭代次数及α值分别为：0.35、2.1、10、0.2，然后测试迭代次数对匹配的影响，其结果如图5所示。通过图5，我们可以看出本文方法只需迭代很少的次数就可以使匹配精度趋于收敛。在本实验中，该方法迭代15次使匹配精度收敛。

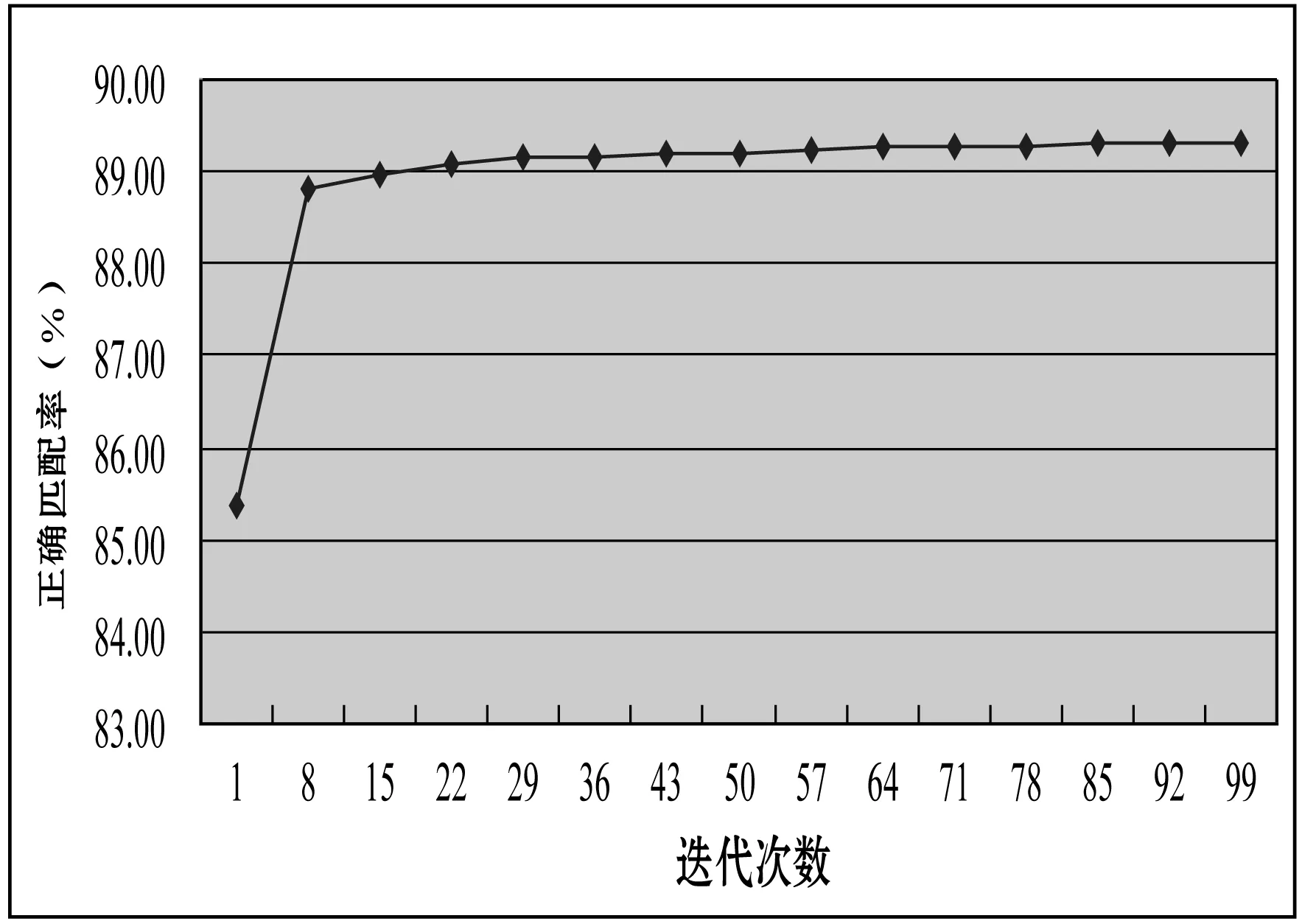
图5 迭代次数分析

3.3 精度分析

本文利用Middlebury网站提供的Tsukuba、Venus、Teddy和Cones对本文提出的立体匹配方法进行了评测，分别在非遮挡区域(nonocc)、不连续区域(disc)和全部区域(all)计算它们的坏点百分比，并与立体匹配方法TSEM[8]、RMCF[11]、AGCP[10]、FTF[9]、TF[12]及FCVT[5]进行对比。图6显示了本文算法的实验结果。从视觉角度上看，计算视差图非常接近于真实视差图，具有较好的匹配效果。表1显示本文方法与其它立体匹配方法的对比结果。对于Tsukuba图像，本文方法在nonocc、all及disc这三个区域的排名分别为：1、2、1；对于Venus图像，本文方法在这三个区域的排名依次

为：3、3、1；对于Teddy图像，本文方法在这三个区域的排名依次为：1、2、1；对于Cones图像，本文方法在这三个区域的排名依次为：3、2、2。根据这些统计数据获得本文方法在这三个区域的平均排名为：2、2、1。通过这一数据可以看出本文方法在不连续区域的匹配效果最佳，这主要是由于本文提出的自适应窗口技术的结果。实验结果表明，本文方法具有较好的匹配性能，而且该方法在不连续区域具有较强的鲁棒性。

(a) 立体像对 (b) 真实视差图 (c) 计算视差图图6 Middlebury实验结果

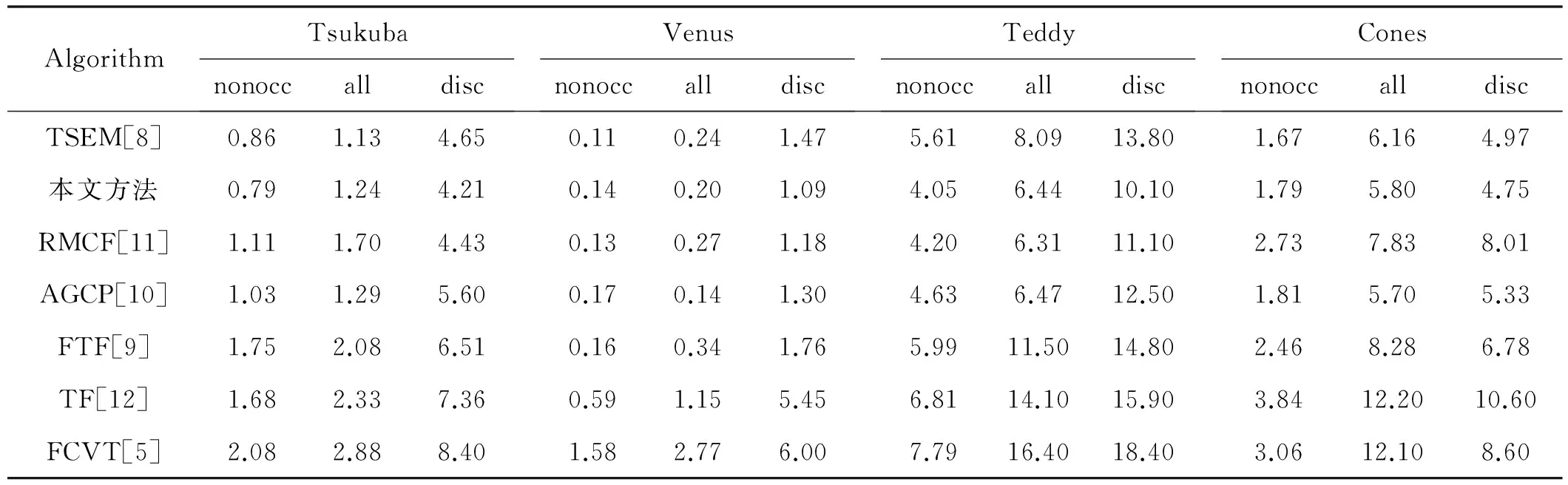
AlgorithmTsukubanonoccalldiscVenusnonoccalldiscTeddynonoccalldiscConesnonoccalldiscTSEM[8]0.861.134.650.110.241.475.618.0913.801.676.164.97本文方法0.791.244.210.140.201.094.056.4410.101.795.804.75RMCF[11]1.111.704.430.130.271.184.206.3111.102.737.838.01AGCP[10]1.031.295.600.170.141.304.636.4712.501.815.705.33FTF[9]1.752.086.510.160.341.765.9911.5014.802.468.286.78TF[12]1.682.337.360.591.155.456.8114.1015.903.8412.2010.60FCVT[5]2.082.888.401.582.776.007.7916.4018.403.0612.108.60

4 结 语

本文提出一种基于迭代指导滤波的立体匹配方法。该方法首先提出一种自适应窗口方法，并结合指导滤波技术用于成本累积，有效提高了立体匹配方法在不连续区域的匹配精度，提高了该方法在不连续区域的鲁棒性。然后提出一种迭代指导滤波方法，根据计算视差逐步优化匹配成本，从而获得了较高精度的视差图。实验结果表明，本文提出的立体匹配方法可以获得较好的匹配效果，且对于不连续区域具有较强的鲁棒性。

[1] Scharstein D, Szeliski R. A taxonomy and evaluation of dense two-frame stereo correspondence algorithms[J].International Journal of Computer Vision,2002, 47:7-42.

[2] 张彦峰, 黄向生,李杭, 等. 基于渐进可靠点生工的散斑图快速立体匹配[J]. 计算机科学, 2014, 41(6A):143-146.

[3] Yoon K J, Kweon I S. Adaptive support-weight approach for correspondence search[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence,2006, 28(4):650-656.

[4] He Kaiming, Sun Jian, Tang Xiaoou. Guided image filtering[J].IEEE Transactions on Pattern Analysis and Machine Intelligence, 2013,35(6):1397-1409.

[5] Hosni A, Rhemann C, Bleyer M, et al. Fast cost-volume filtering for visual correspondence and beyond[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence,2013, 35(2): 504-511.

[6] Mattoccia S, Giardino S, Gambini A. Accurate and efficient cost aggregation strategy for stereo correspondence based on approximated joint bilateral filtering[C]// The Ninth Asian Conference on Computer Vision. Berlin Heidelberg: Springer, 2010:371-380.

[7] Richardt C, Orr D, Davies I, et al. Real-time spatiotemporal stereo matching using the dual-cross-bilateral grid [J].Lecture Notes in Computer Science, 2010, 6313:510-523.

[18] Mozerov M G,Weijer J V. Accurate stereo matching by two-step energy minimization [J].IEEE Transactions on Image Processing, 2015, 24(3):1153-1163.

[9] Chen Dongming, Ardabilian M, Chen Liming. A fast trilateral filter-based adaptive support weight method for stereo matching [J]. IEEE Transactions on Circuits and Systems for Video Technology, 2015,25(5):730-743.

[10] Shi Chenbo, Wang Guijin, Yin Xuanwu, et al. High-accuracy stereo matching based on adaptive ground control points[J]. IEEE Transactions on Image Processing, 2015, 24(4):1412-1423.

[11] Dinh V Q, Nguyen V D, Jeon J W. Robust matching cost function for stereo correspondence using matching by tone mapping and adaptive orthogonal integral image[J].IEEE Transactions on Image Processing, 2015, 24(12):5416-5431.

[12] Yang Q. Stereo matching using tree filtering[J].IEEE Transactions on Pattern Analysis & Machine Intelligence, 2015, 37(4):834-846.

ASTEREOMATCHINGMETHODBASEDONITERATIVEGUIDEDFILTER

Li Jinfeng1Bian Jilong21

(CollegeofComputerandInformationTechnology,MudanjiangNormalUniversity,Mudanjiang157011,Heilongjiang,China)2(CollegeofInformationandComputerEngineering,NortheastForestryUniversity,Harbin150040,Heilongjiang,China)

This paper presents a stereo matching method based on iterative guided filter aimed at improving the accuracy of stereo matching. In this method, an adaptive window method is used to make an adaptive choice of a support window according to grayscale variation in images. Secondly, raw matching cost is aggregated by a guided filter and disparities are computed by the “winner-take-all” method. Thirdly, matching cost is modified on the basis of the computed disparities and is again aggregated to calculate disparities. Finally, this process is repeated until the maximum number of iterations is reached. Experimental results show that the proposed method can achieve an accurate disparity map, and has a strong robustness to the discontinuous regions in images.

Stereo matching Adaptive window Guided filter Adaptive weight

TP3

A

10.3969/j.issn.1000-386x.2017.09.036

2016-09-08。国家自然科学基金项目(51575097);牡丹江师范学院青年骨干基金项目(QG2014001);黑龙江省自然科学基金项目(E2016002)。李金凤，副教授,主研领域：图像处理，计算机视觉，立体匹配。边继龙，讲师。