基于总体平均经验模态分解的语音增强算法研究

陈建明 杨 龙

(装甲兵工程学院信息工程系 北京 100072)

基于总体平均经验模态分解的语音增强算法研究

陈建明 杨 龙

(装甲兵工程学院信息工程系 北京 100072)

总体平均经验模态分解EEMD(Ensemble Empirical Mode Decomposition)虽然能够在一定程度上抑制模态混淆，但添加的白噪声不能被完全中和，对所有本征模态函数IMF(Intrinsic Mode Function)分量进行集成平均等增加了计算工作量。基于EEMD和结合小波阈值去噪思想，提出改进的EEMD方法。首先对原始信号进行EEMD分解，得到一系列IMF分量；其次对筛选后的每个IMF计算噪声强度；然后采用小波启发式阈值估计噪声并计算阈值；最后以软阈值的方式滤除每个IMF中噪声并重构信号还原出增强的语音。通过分析仿真信号和实测信号，结果表明：该算法对带噪语音有很好的滤波效果，与其他同类算法相比提高信噪比2～4 dB。

总体平均经验模态分解(EEMD) 小波阈值去噪 语音增强算法

0 引 言

20世纪60年代，人们对语音通信质量有了更高的要求，语音增强技术成为了研究的热点，多种语音增强算法不断涌现。从70年代开始，研究者以语音生成模型为基础，根据短时平稳性相继提出了一些常用的传统语音增强算法，如谱相减法、自适应滤波法等。之后，研究者采用统计模型来估计语音信号谱，此类算法增强效果相对较好，但是需要先验性经验和训练数据且计算量偏大，处理时间长，因此，常用于信号识别处理。80年代，小波变换理论日趋成熟，研究者将研究重心转移到更适合非平稳信号分析的小波变换上。1998年，美籍华人Huang等创造性地提出一种新的信号处理方法——经验模态分解EMD(Empirical Mode Decomposition)[1]。该方法实现了对非平稳信号的平稳化处理，不但具有小波变换的多频率分辨率，且具有良好的自适应特性。虽然EMD对非平稳信号的分解有诸多优势，但是为了能够实现最优的分解效果且最大限度地保留原信号的信息，在利用EMD进行语音信号处理的时候必须要克服EMD最容易发生端点效应和混叠效应问题。针对EMD产生的混叠效应问题，Wu和Huang在2009年提出了总体平均经验模态分解EEMD方法[2-3]，EEMD是针对在EMD基础上通过噪声辅助产生的改进算法来克服模态混叠问题。EEMD在信号分解与检测、故障诊断、信号预测，以及语音去噪等许多领域都有较大的应用[4-8]，在使用中学者为了解决本领域的信号处理问题，提出了许多改进的EEMD算法。文献[9]成对地添加符号相反的白噪声到目标信号，大大减小了重构误差；文献[10] 通过提取信号中的高频成分来确定加入白噪声的幅值,再根据减小白噪声影响的统计规律得到总体平均次数，然后引入有限带宽高斯白噪声，实现对信号的快速准确分解；文献[11] 以极值点分布特性为评价参数,自适应确定EEMD方法中高斯白噪声优化幅值；文献[12]结合时域航空电磁信号的衰减特性，采用 Savitzky-Golay平滑滤波完成对时域航空电磁信号降噪；文献[13] 采用“3σ法则”，对含噪信号先“粗筛”后进行“细筛”等实现对低信噪比下的谐波检测。这些算法针对各领域的信号特性，采用多种组合方法，克服EEMD混叠效应问题达到去噪的目的。本文在EEMD的基础上，结合小波分解软阈值的思想，采用启发式阈值计算的方法，提出了基于EEMD的改进算法。该算法的启发式阈值去噪对带噪语音信号具有自适应性，有较好的滤波效果，与其他同类算法相比提高信噪比2～4 dB，能满足实际应用需要。

1 EEMD的基本原理

根据Huang对于EMD引入白噪声改进的思想，可将改进后的EEMD的原理[14]归纳如下：

1) 对待分解的信号x(t)加入一组白噪声wi(t)(i=1-N，N为次数)，构成一个总体X(t)。

Xi(t)=x(t)+wi(t)

(1)

2) 对式(1)中生成的总体Xi(t)进行EMD分解，得到每个IMFj(j=1-K)分量。

(2)

式中cij(t) 为第i次加入白噪声后，分解得到的第j个IMF。

3) 重复步骤1)～2)，每次加入不同的白噪声。

4) 取相应的IMF的均值作为最终的IMF组。

(3)

对于EEMD来说，在噪声幅度一定的条件下，总体个数越多，则平均后所得的IMFs越接近真实信号分量。但是需要注意如果加入的噪声幅度过小，信噪比较高，则噪声将无法影响极值点的选取，从而加入的白噪声失去了弥补尺度的作用，因此无法克服模态混叠的作用而适得其反。

2 基于EEMD的小波软阈值语音增强

带噪语音通过EEMD分解到不同的时间尺度上，因而整个信号的振动模态可根据频率的高低依次呈现在不同的IMF上，这样可以直观地看到语音和噪声在不同尺度上的具体表现。通常，语音信号的主要信息大多分布在较大的时间尺度且有限个IMF中，因此，对所需的IMFs重构来还原信号可为后续的信号处理提供有效支撑。

2.1 小波阈值去噪原理

语音根据其信号特征可知能量集中，从而通过小波分解后所得的小波系数较大；而噪声能量通常比较分散，分解所得的小波系数较小且随着分解尺度的增大，噪声分解后的小波系数越小，即噪声分量主要分布在小尺度的小波系数中。基于此，利用阈值的思想将噪声系数进行限制，只保留信号的小波系数以达到去噪的目的。阈值去噪的实现思想即对大于和小于阈值的小波系数作不同的处理。通常，阈值函数分为硬阈值和软阈值[15]。

硬阈值定义为：

(4)

软阈值定义为：

(5)

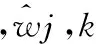
1) 固定阈值

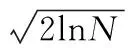
(6)

式中，σ表示噪声强度的估计，由噪声的方差求得，N表示分解系数的长度。在EMD分解的前提下，σ的求得公式如下：

(7)

式中，j表示EMD分解尺度的序数，N为IMF的长度。

2) 无偏似然估计阈值

其步骤为：先对信号中所有数据的绝对值按照由小到大的顺序排列，然后对排列好的数据依次求平方得到新的数据序列，表示为：

sx2(k)=(sort(x(n)))2k=1,2,…,N

(8)

若选取阈值为式(8)产生的序列中的第k个值，则可表示为：

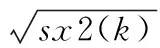
(9)

而这第k个值作为阈值所产生的风险可表示为：

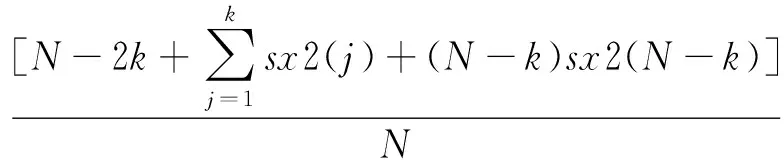
(10)

根据式(10)可获得风险曲线，其中风险最小的点所对应的值则为无偏估计的阈值，可表示为：

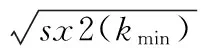
(11)

3) 启发式阈值

该阈值综合了前两种阈值计算的思想，启发式的选取最优预测的阈值，具体公式如下：

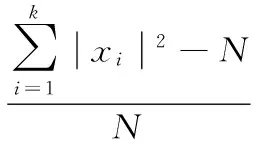
(12)

(13)

根据式(12)和式(13)，当μ<ν时，信噪比较低，采用固定阈值，反之，采用无偏似然估计阈值。

根据语音信号的非线性非平稳特性，启发式阈值具有固定阈值和无偏似然阈值两种估计的优势，可根据信号的特性自发进行估计。因此，本文采用的类小波阈值的阈值选取方法为启发式阈值。

2.2 基于EEMD的类小波软阈值语音增强

由以上描述可知，带噪语音中的语音信号和噪声信号根据其特性在EEMD分解后，语音信号随着分解尺度的增加，有效的语音分量体现的越多，而噪声的分量随着分解尺度的增加所占的信息不断减少，尤其对于含有大量高频分量的噪声特别有效。通过选取适当的IMF，即提取出可用的分解尺度上的信号分量进行重构，可有效去除无用的噪声分量。

在去除无用的IMF基础上，本文提出了小波阈值思想设定阈值来消除噪声。改进的算法的具体步骤可表示为：

步骤1首先对原始信号进行EEMD分解，得到一系列IMF分量；

步骤2对筛选后的每个IMF用式(7)计算噪声强度；

步骤3采用小波启发式阈值估计噪声并计算阈值；

步骤4以软阈值用式(5)的方式滤除每个IMF中噪声；

步骤5重构信号并还原出增强的语音。

3 语音增强仿真实验

3.1 实验素材

实验采用的纯净语音为男声“装甲兵工程学院”。其采样频率为8 kHz，参考噪声来自NoiseX92噪声库，以坦克内部噪声m109进行仿真实验。

1) 纯净语音的时频信息

纯净男声“装甲兵工程学院”的时域波形、FFT谱和语谱图如图1所示，从FFT谱中可以看出语音信号的频率范围在20 Hz～8 kHz，从频谱中可知该语音的频率主要集中在1 k～4 kHz，以中低频为主。

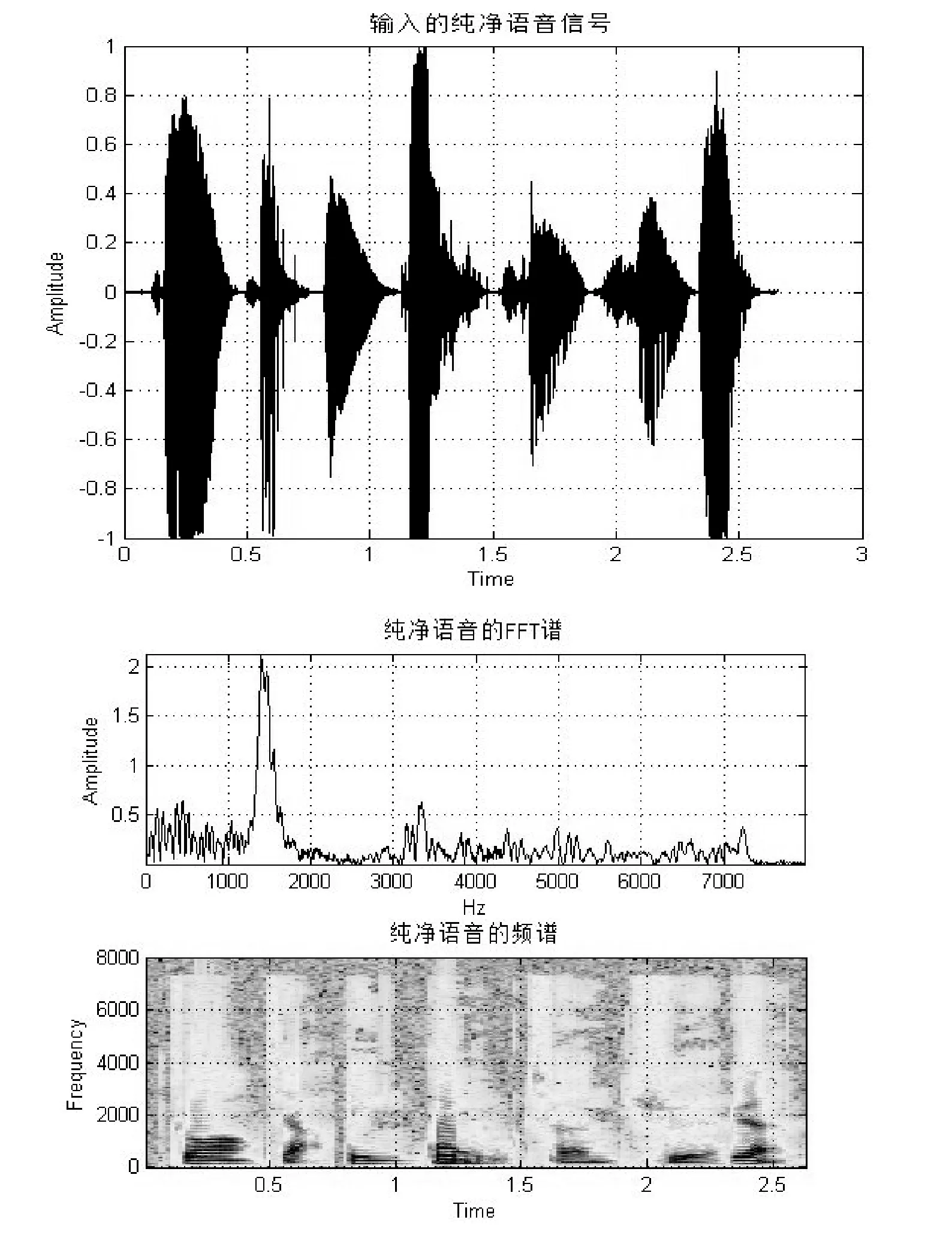
图1 纯净语音男声的时域波形、FFT谱和频谱

2) 噪声m109的时频信息

噪声m109的时域波形和频谱如图2所示，噪声m109是时速30 km/h行驶的M109坦克的内部背景噪声。从图2中可看出噪声幅值和频率均呈现一定的机动性，m109噪声的频率几乎全部集中在1 kHz以下，但是还有部分高频分量，在5 kHz、8 kHz、9 kHz附近有所体现。

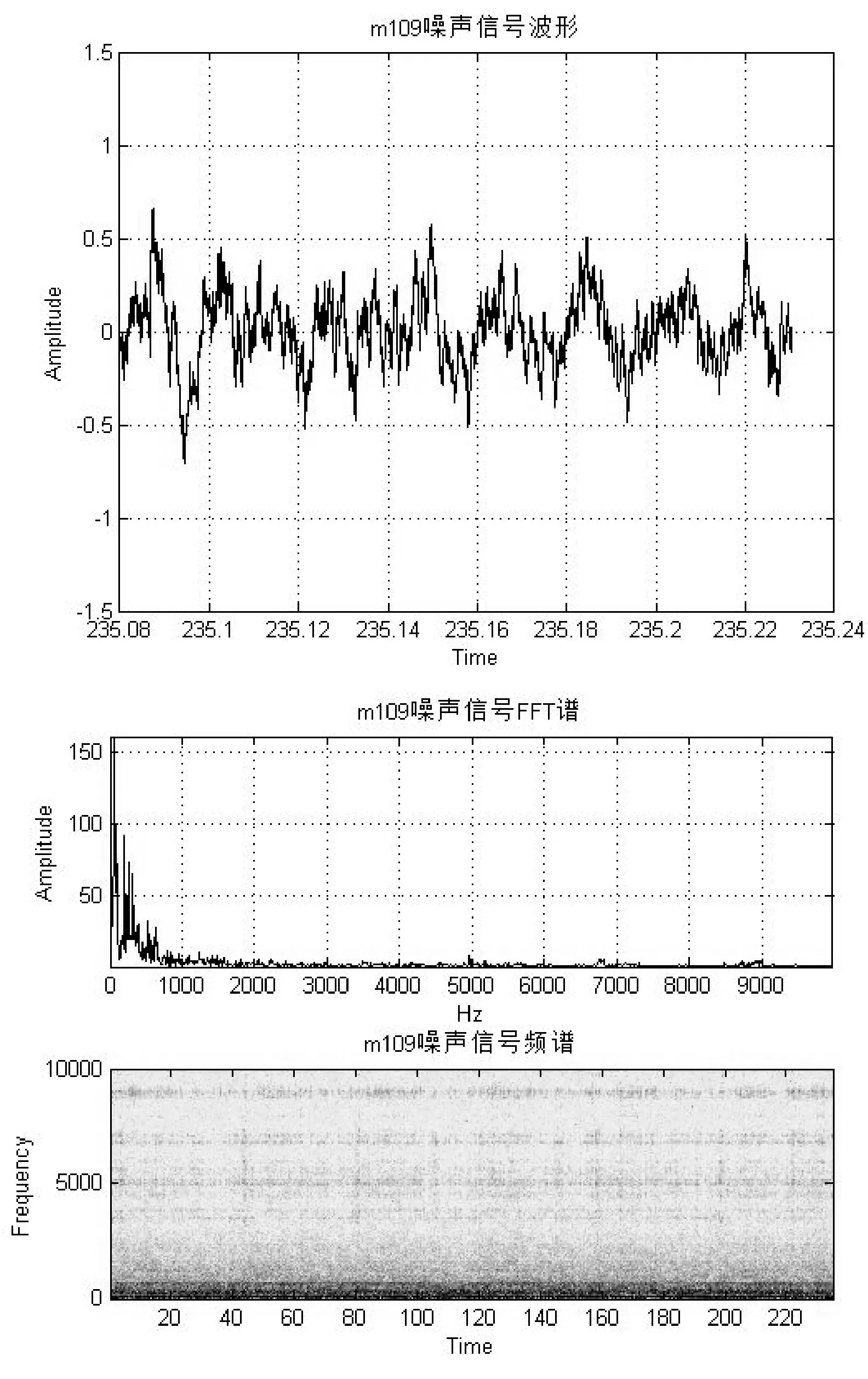
图2 噪声m109的时域波形和频谱

3.2 仿真结果与分析

为了测试本文提出的基于EEMD的类小波软阈值语音增强算法的性能，现将上节的纯净语音和参考噪声合成0 dB和5 dB的带噪语音进行仿真实验，并以目前常用的LMS和MMSE语音增强算法作为参考进行对比。

1) SNR=0时的仿真结果

图3和图4为在m109噪声条件下通过本文算法得到的增强后语音的时域波形和频谱，从带噪语音的频谱来看，中高频都受到噪声的干扰，原语音信号的低频部分受到更大的影响。从增强后的频谱来看，中高频的噪声影响被有效的抑制，而低频的影响也由阈值限定有效去除。

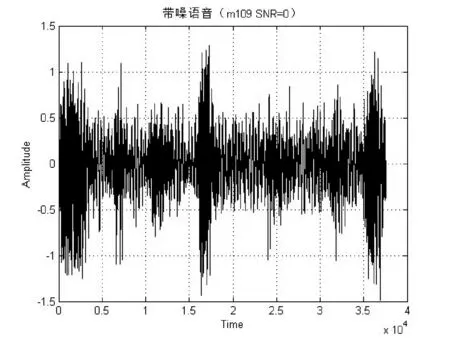
图3 m109(SNR=0)生成带噪语音波形及EEMD分解结果

图4 m109(SNR=0)噪声下本文算法增强后语音时域波形和语音频谱

图5为LMS的增强仿真结果，从时域波形上可以显示出对噪声有一定的抑制，但是频谱上呈现的增强效果不太明显。图6为MMSE的增强结果，从时域和频谱的仿真结果来看，增强效果不错，频谱上高频有少许噪点，但对于原始语音的还原度很好。

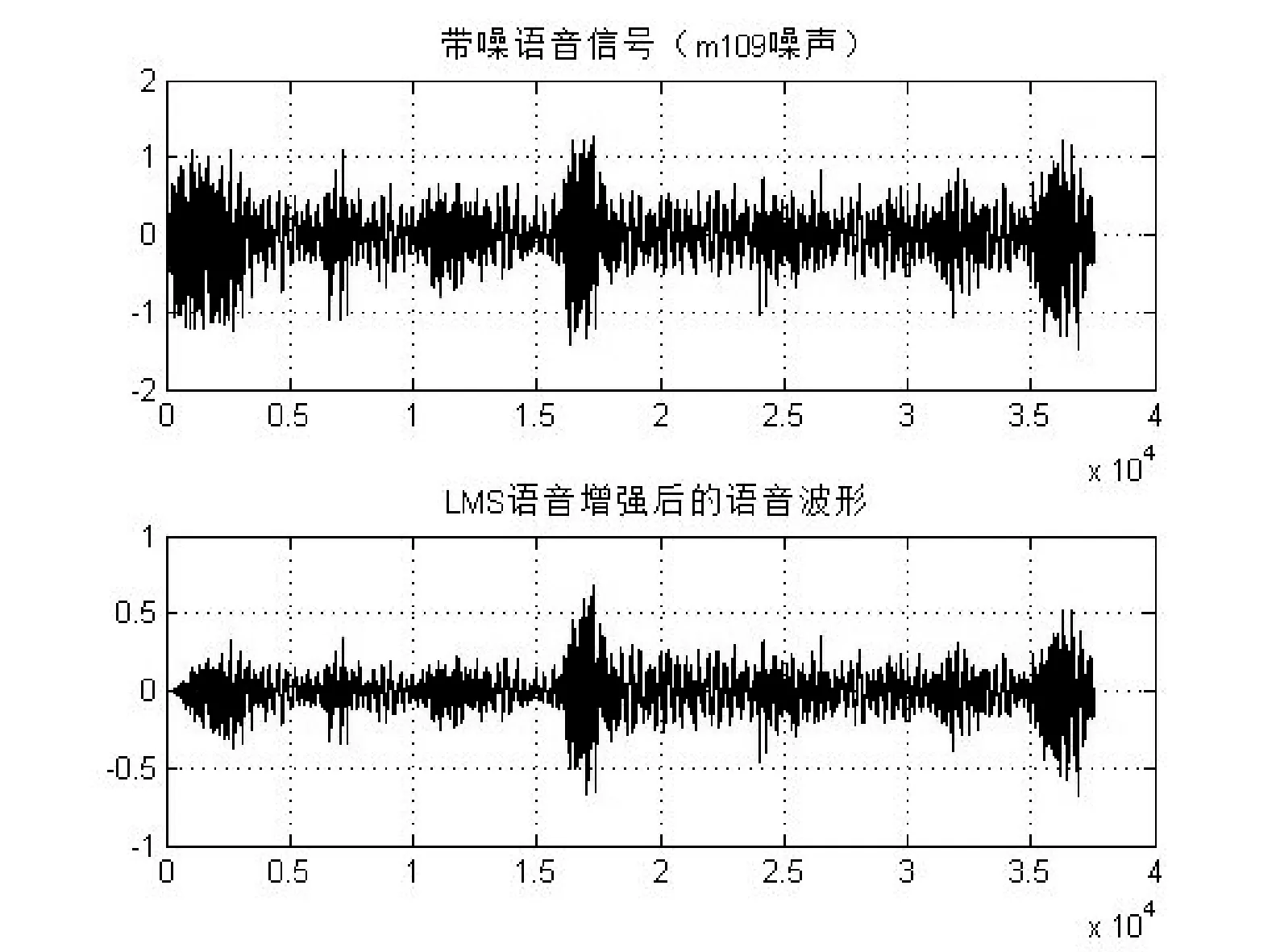
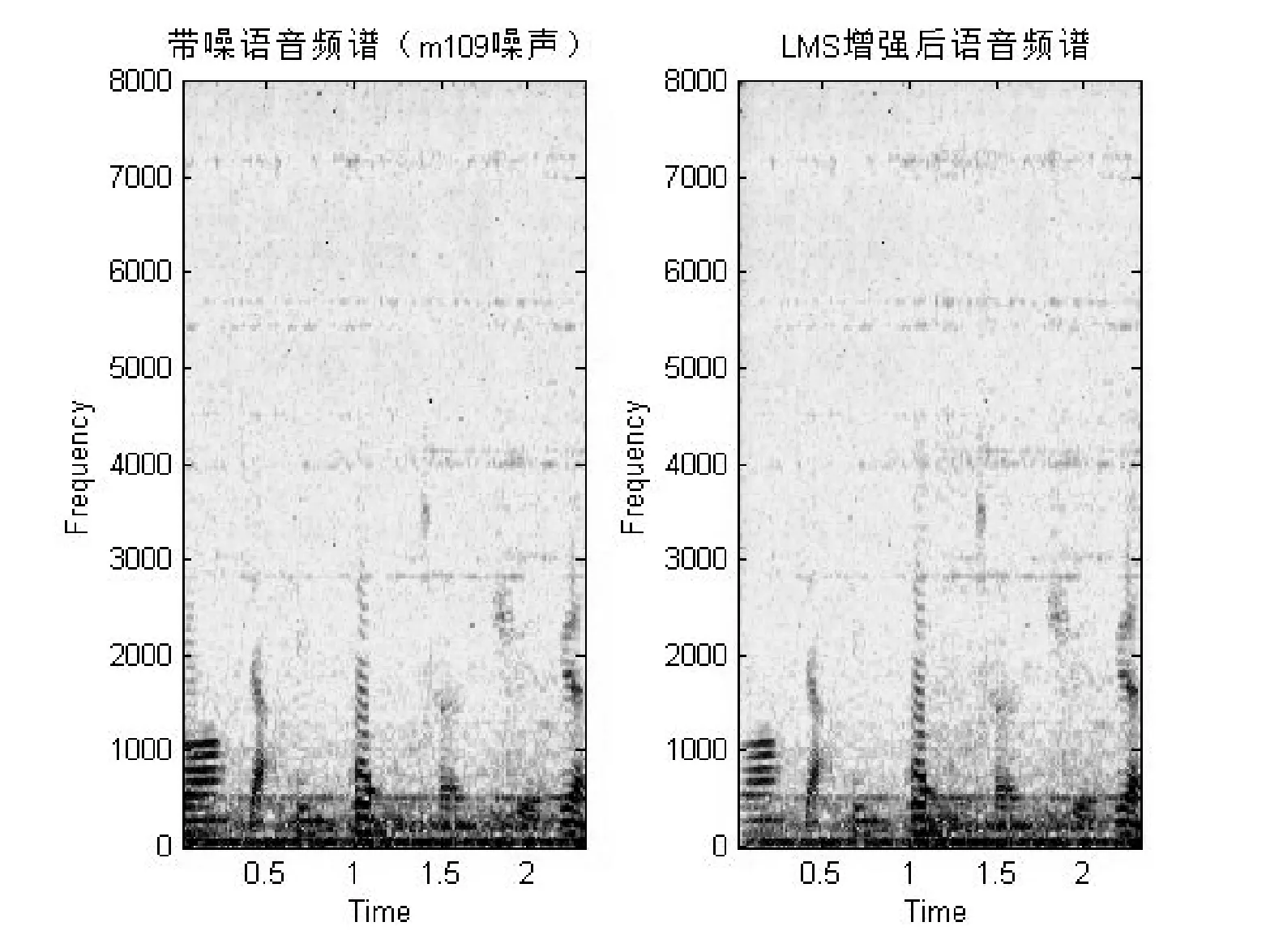
图5 m109(SNR=0)噪声下LMS语音增强时域波形和频谱

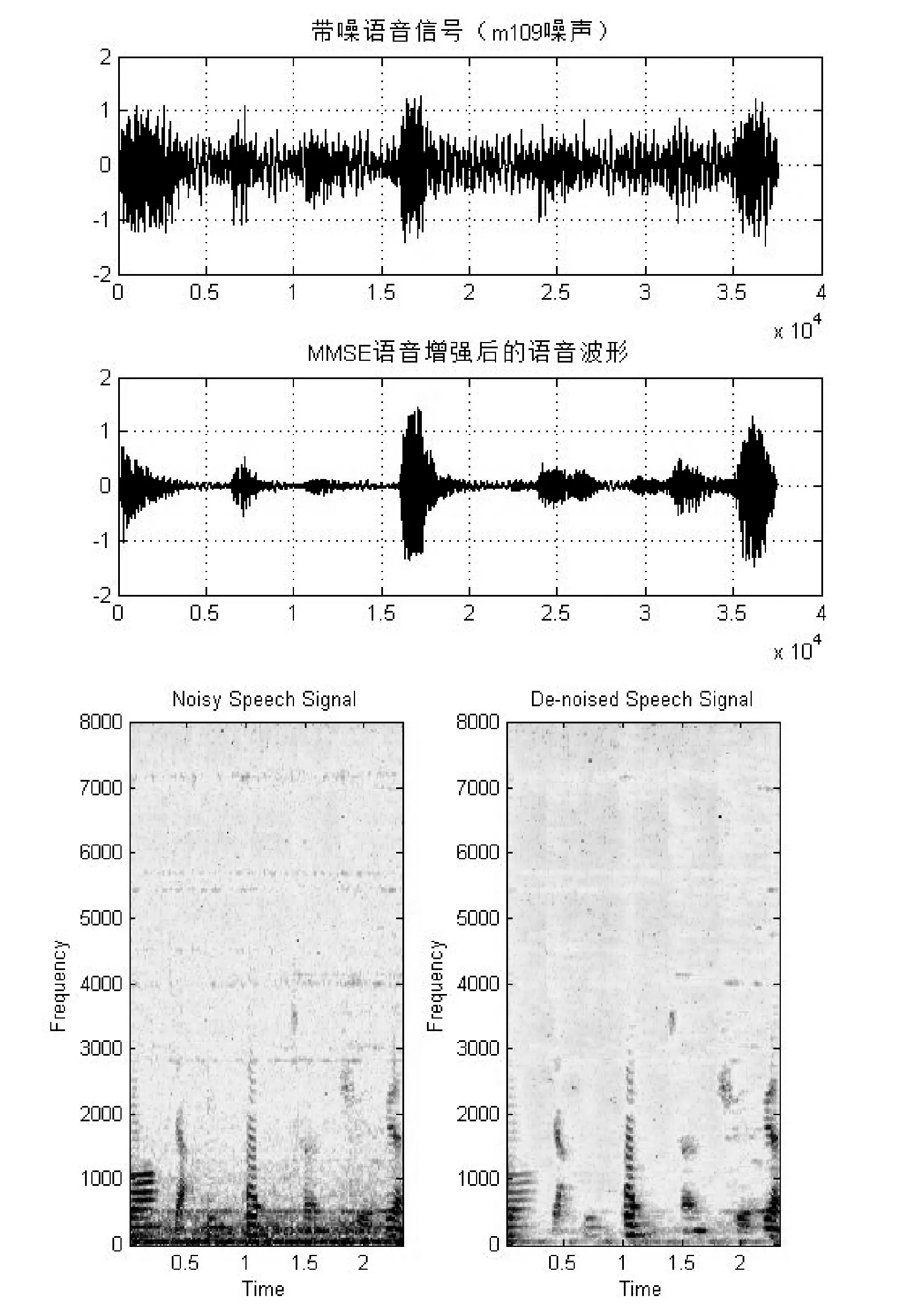
图6 m109(SNR=0)噪声下MMSE语音增强时域波形和频谱

2) SNR=5 dB的仿真结果

图7(a)为m109噪声在SNR=5条件下通过本文算法得到的增强后语音频谱，通过频谱可发现本文算法去噪效果有效。图7(b)和(c)为LMS和MMSE的增强结果，相比较于SNR=0的情况下，增强效果有所改善。

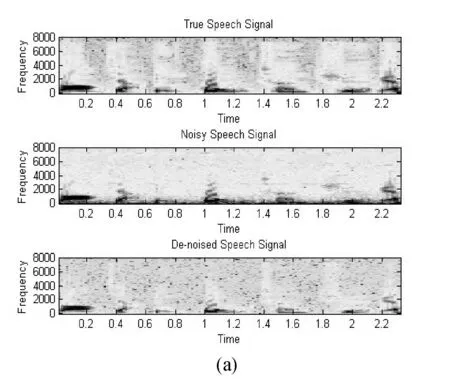
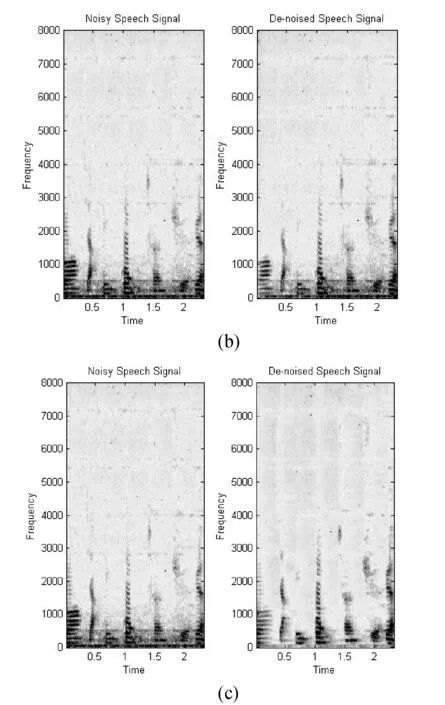
图7 m109(SNR=5)噪声下本文算法、LMS、MMSE后语音增强频谱

通过上述SNR=5条件下的频谱图可以看出，本文算法对高频噪声的滤除非常有效，但是可能导致高频的分量过少影响可懂度。从增强效果来讲，本文算法优于MMSE和LMS，表1为SNR=5时的三种算法实验的信噪比结果。

表1 三种算法增强后输出信噪比结果

4 结 语

从仿真实验看，由于采用EEMD的滤波特性，对于噪声而言，对高频的去噪效果非常显著，从图中的三种方法的频谱对比可知，噪声频率相对在低频范围。如图7所示，本文算法信噪比改善的效果要好于LMS和MMSE，但是从频谱上来看，过多的高频分量被滤除，导致可懂度有所下降。

从EEMD分解图中，噪声根据参考尺度明显分解至中频或低频部分，从而需通过小波软阈值进一步滤除，在增强后的语音中还会残存一部分噪声分量。

利用本文算法还对NoiseX92噪声库中的餐厅噪声babble、F16舱内噪声f16、军用车辆噪声leopard等进行了仿真实验，结果表明该算法与其他同类算法相比提高信噪比2～4 dB，对带噪语音有很好的滤波效果。

[1] Huang N E,Shen Z,Long S R,et al.The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J].Proceedings of the Royal Society A Mathematical Physical & Engineering Sciences,1998,454(1971):903-995.

[2] Huang N E,Wu Z.A review on Hilbert-Huang transform: Method and its applications to geophysical studies[J].Reviews of Geophysics,2008,46(2):RG2006.

[3] Wu Zhaohua,Huang N E.Ensemble empirical mode decomposition:a noise-assisted data analysis method[J].Advances in Adaptive Data Analysis,2009,1(1):1-41.

[4] Franzke C.Long-range dependence and climate noise characteristics of Antarctic temperature data[J].Journal of Climate,2010,23(22):6074-6081.

[5] Lei Y,He Z,Zi Y.Application of the EEMD method to rotor fault diagnosis of rotating machinery[J].Mechanical Systems & Signal Processing,2009,23(4):1327-1338.

[6] 李海涛,王成国,许跃生,等.基于EEMD的轨道—车辆系统垂向动力学的时频分析[J].中国铁道科学,2007,28(5):24-30.

[7] Lotfi S,Jaouher Ben A,Farhat F.Bi-spectrum based-EMD applied to the non-stationary vibration signals for bearing faults diagnosis[J].Isa Transactions,2014,53(5):1650-1660.

[8] 张彦霞,肖清泰,徐建新,等.基于经验模态分解的小波神经网络预测模型[J].计算机应用与软件,2016,33(10):284-287.

[9] 郑近德,程军圣,杨宇.改进的EEMD算法及其应用研究[J].振动与冲击,2013,32(21):21-26.

[10] 何星,王宏力,姜伟.改进的自适应EEMD方法及其应用[J].系统仿真学报,2014,26(4):869-873.

[11] 孔德同,刘庆超,雷亚国,等.一种改进的EEMD方法及其应用研究[J].振动工程学报,2015,28(6):1015-1021.

[12] 张婷,李双田.改进的EEMD算法在时域航空电磁信号降噪中的研究[J].信号处理,2016,32(7):771-778.

[13] 孙曙光,庞毅,王景芹.改进的EEMD去噪方法及其在谐波检测中的应用研究[J].电工电能新技术,2016,35(4):67-74.

[14] 张梅军,唐建,何晓晖.EEMD方法及其在机械故障诊断中的应用[M].北京:国防工业出版社,2015.

[15] 王蓓,张根耀,李智.新小波阈值函数在医学图像去噪中的应用[J].计算机系统应用,2014,23(7):175-179.

RESEARCHOFSPEECHENHANCEMENTALGORITHMBASEDONENSEMBLEEMPIRICALMODEDECOMPOSITION

Chen Jianming Yang Long

(DepartmentofInformationEngineering,AcademyofArmoredForceEngineering,Beijing100072,China)

Ensemble Empirical Mode Decomposition (EEMD) can restrain mode mixing of EMD at a certain level, however, the calculation amount of all ensemble IMF (Intrinsic Mode Function) grows due to the white noise unneutralized completely. Therefore, based on EEMD and wavelet soft threshold, we presented a modified EEMD algorithm for speech enhancement. First, the original signal was decomposed using EEMD, and a series of IMFs were acquired; second, noise intensity of the each screened IMF was calculated; third, using wavelet heuristic threshold method, the noise was estimated and the threshold was calculated; finally, noise of every IMF was filtered with wavelet soft threshold method, and speech signal was restructured. By analyzing the simulation signal and the measured signal, we show that the algorithm has a good filtering effect on the speech enhancement, and improves the SNR 2 ～ 4dB compared with other similar algorithm.

Ensemble empirical mode decomposition(EEMD) Wavelet soft threshold Speech enhancement algorithm

TP319 TN911.7

A

10.3969/j.issn.1000-386x.2017.09.064

2016-11-24。陈建明，教授，主研领域：信号与信息处理。杨龙，助教。