基于可变设计参数的平面Acrobot位置快速控制方法

王亚午，赖旭芝，吴敏

(1.中国地质大学(武汉) 自动化学院，湖北 武汉 430074；2.复杂系统先进控制与智能自动化湖北省重点实验室，湖北 武汉 430074)

基于可变设计参数的平面Acrobot位置快速控制方法

王亚午1,2，赖旭芝1,2，吴敏1,2

(1.中国地质大学(武汉) 自动化学院，湖北 武汉 430074；2.复杂系统先进控制与智能自动化湖北省重点实验室，湖北 武汉 430074)

为平面Acrobot系统(无重力项)提出一种基于可变设计参数的快速位置控制方法。首先，根据平面Acrobot系统的完全可积特性，获取驱动关节与欠驱动关节的角速度和角度约束关系。其次，根据系统的物理结构，推导出末端点坐标位置和两关节角度之间另一类约束关系。然后，基于这两类约束关系，利用粒子群优化算法求取目标位置对应的两杆目标角度。接着，通过构造李雅普诺夫函数为平面Acrobot系统设计控制器，并根据控制器中设计参数的特性，选择一个可变的设计参数，减少控制系统到达目标的时间。利用连杆角速度和角度约束关系，通过控制驱动杆到目标角度同时连带控制欠驱动杆到目标角度，实现系统的控制目标。最后，仿真结果验证所设计控制方法的有效性和快速性。

平面欠驱动机械系统；平面Acrobot；位置控制；粒子群优化算法；非线性函数

0 引 言

欠驱动机械系统是指控制输入个数少于系统自由度个数的非线性系统[1-3]，它能够利用较少的驱动装置完成控制任务，具有重量轻、低能耗、灵活等优点；然而，驱动装置的减小使得该类系统控制器设计的难度增加，很多适用于全驱动系统的控制方法无法直接推广到这类系统中。而目前，国内外对垂直欠驱动机械系统(含重力项)的研究较为成熟[4-6]，但对平面欠驱动机械系统(不含重力项)的研究还在起步阶段。

针对垂直欠驱动机械系统，现在普遍采用的控制方法是分区控制方法[1,7-8]，即将控制空间划分为摇起区和平衡区。针对摇起区的控制问题，主要采用基于系统模型[9]、运动姿态[10]、系统能量[11]和鲁棒性能[12]等指标的智能控制方法；而平衡区的控制主要通过在平衡点附近将系统近似线性化，并采用线性二次调节器(LQR)来实现系统的稳定控制[13]。而对于平面欠驱动机械系统的控制问题，由于其动力学模型不含重力项，导致其在水平面内的任意静止姿态都为它的平衡点，并且其在平衡点附近的线性近似模型不满足可控条件[14]，无法采用垂直欠驱动系统中已成熟的LQR方法实现系统稳定控制。

早期研究中学者们为降低平面欠驱动系统的控制难度，在模型中考虑摩擦力[15-16]或者在欠驱动关节加装制动装置或弹簧[17-18]，以此完成平面欠驱动系统的控制任务；但这些方法改变了系统的欠驱动性质。文献[19]通过为平面Pendubot离线规划一条轨迹，并利用滑模控制技术实现系统轨迹的稳定跟踪。文献[20]针对平面Pendubot的控制问题，通过分解系统的运动，利用分层模糊控制器实现系统的控制。但这些研究大多针对第一关节为驱动的平面机械系统，而对于第一关节为欠驱动的平面机械系统的研究则较少。Oriolo等人[21]对平面欠驱动系统的可积性进行了初步研究，并证明了第一关节为欠驱动的平面Acrobot具有完全可积分的特性。之后，文献[22]基于平面Acrobot的完全可积特性，提出了基于轨迹特性的平面Acrobot运动控制方法，但从其仿真结果来看，系统各个状态到达稳定的时间较长，并且没有提出基于末端点位置获取连杆角度的方法。

基于文献[21]和文献[22]的研究，为了克服系统控制时间较长的问题，提出一种快速实现末端点位置控制的方法。首先，基于平面Acrobot的完全可积特性，获取驱动杆和欠驱动杆的角速度约束关系和角度约束关系，即通过控制驱动杆(第二连杆)实现欠驱动杆(第一连杆)的连带控制。然后，根据系统的物理结构，获取末端点位置和两杆角度之间的约束关系。基于系统这两类约束关系，利用粒子群优化(PSO)算法求取末端点目标坐标位置对应的两杆目标角度值。最后，通过构造李雅普诺夫函数设计控制器，并根据控制器中设计参数的特性，将设计参数设计成一类非线性函数，减少控制系统到达目标的时间。通过控制驱动杆达到目标角度同时连带控制欠驱动杆达到目标角度，实现系统末端点位置控制任务。仿真结果验证所提控制方法不仅能够完成系统末端点的位置控制任务，并且控制时间较短。

1 系统模型

第一关节为欠驱动的平面两连杆系统(平面Acrobot)的物理结构如图1所示：

图1 平面Acrobot系统Fig.1 Planar Acrobot system

对于第i连杆(i=1,2)：mi表示质量；Li表示长度；li表示第i连杆的质心到第i关节的长度；Ji表示转动惯量；q1为第1连杆相对于坐标y轴方向的角度，q2为第2连杆相对于第1连杆延长线方向的角度；(x,y)为系统末端点坐标位置。

根据欧拉-拉格朗日公式可得平面Acrobot系统的动力学方程为

(1)

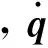
上述各元素的具体形式如下：

M11(q)=a1+a2+2a3cosq2，

M12(q)=M21=a2+a3cosq2，

M22(q)=a2，

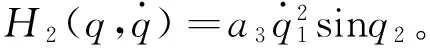
其中a1、a2、a3为系统结构参数，具体表达式如下：

a3=m2L1l2。

由于平面Acrobot系统运动时处于水平面内，不含重力项，因而简化了系统的动力学模型；但重力项的缺失会使得系统在水平面内的任意静止姿态都成为它的平衡点，并且也导致在平衡点附近的线性近似模型不满足线性可控条件[15]，故无法采用垂直欠驱动系统中已成熟的LQR方法实现系统的稳定控制。因此，为实现平面Acrobot系统从任意初始位置到目标位置的控制，下面将基于平面Acrobot的完全可积特性获取系统驱动杆与欠驱动杆之间的状态约束关系，并基于此约束关系提出平面Acrobot的位置控制方法。

2 约束关系分析

由动力学方程(1)可知，系统的二阶微分约束为

(2)

系统惯性矩阵的欠驱动部分Mu(q)=[M11(q),M12(q)]对时间求导，可得

(3)

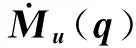
(4)

将式(4)代入到式(2)中得

(5)

式(5)对时间积分得

(6)

(7)

从式(7)可知，当第二杆的角速度为0时，第1杆的角度速度也为0，即只要能控制第2杆到静止状态，平面Acrobot系统就能稳定。

而M11(q)是正定对称矩阵M(q)对角线上的元素，则有M11(q)>0。又因M(q)不包含q1，所以式(7)可写成

(8)

式(8)对时间积分，可得

(9)

其中A1和A2是与系统结构参数有关的量，具体形式分别为：

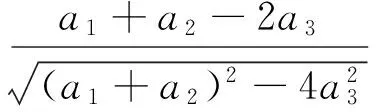
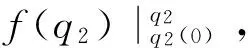
(10)

其中floor(·)为向下取整函数。

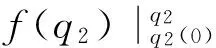
1)k≥0时，

f(q2)-f(q2(0))+kπ

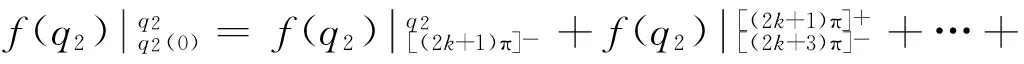
f(q2)-f(q2(0))+kπ

(11)

其中，c=-A1f(q2(0))+q1(0)+q2(0)/2。

从角度约束关系式(11)可知，当控制驱动杆(第2杆)到达某个角度，欠驱动杆(第1杆)也将被连带控制到某个角度，即可通过控制驱动杆来实现欠驱动杆的连带控制。下面，通过分析系统的几何结构，同时结合角度约束关系式(11)，来获取系统末端点目标坐标位置对应的两杆目标角度。

3 目标角度求解

在讨论目标角度求解之前，首先需建立末端点的坐标位置(x,y)和两杆角度q1,q2之间的关系，如图2所示。

图2 平面Acrobot物理结构简图Fig.2 Physical structure diagram of planar Acrobot

根据平面Acrobot的物理结构简图，运用几何知识可获得末端点坐标位置与两杆角度之间的约束关系为：

(12)

因此，当系统末端点的目标坐标位置设计为(xd,yd)时，为寻找同时满足约束关系式(11)和式(12)的目标角度q1d和q2d，首先将式(11)代入式(12)中得：

(13)

然后根据式(13)可定义如下目标函数：

h(q2)=|x-xd|+|y-yd|。

(14)

可知，h(q2)=0的解就是驱动杆目标角度q2d。当将q2d代入约束关系式(11)中，即可求得对应的欠驱动杆目标角度q1d。

考虑到直接求解h(q2)=0较为困难，并且在误差允许的范围内(h(q2)≤e1)，目标坐标位置对应的目标角度具有多解性。因此，这里选取粒子群优化算法作为求解方法。记sj=q2为粒子的位置。从而，第j(j=1,2,…,n)个粒子的进化方程为：

(15)

其中：w为惯性权重；c1和c2为权重因子；r1和r2为在[0,1]当中的随机值；sj(K)表示第j个粒子的位置；vj(K)表示第j个粒子的速度；pj代表第j个粒子的个体历史最优位置；pg表示群体历史最优位置；K为粒子进化代数；n为粒子群的大小。

个体历史最优位置更新规则：

(16)

群体历史最优值更新规则

pg=argmin{h(pj)}。

(17)

为防止粒子的进化速度过大，这里加入速度限制方程，如下式所示：

|vj(K+1)|≤vmax。

(18)

其中vmax为正的常数。

求解两杆目标角度的算法步骤如下：

1)初始化n个粒子的初始位置sj(0)与初始速度vj(0)及个体历史最优位置pj与群体历史最优位置pg。

2)按照粒子的进化方程式(15)来更新各个粒子的位置和速度，由式(18)来限制粒子进化速度。当进化代数K=Kmax，退出程序。

3)将新一代n个粒子的位置代入到目标函数h(·)中，求得此新一代n个粒子的适应度值。

4)根据各个粒子的适应度值，按照式(16)和式(17)来更新个体历史最优位置pj和群体历史最优位置pg。

5)当粒子群中最大的适应度值小于或等于e1时，群体历史位置pg即为驱动杆目标角度q2d，程序转到第六步；否则，转到第2步。

6)将q2d代入到公式(11)中，求出相应欠驱动杆目标角度q1d，退出程序。

当控制驱动杆到达目标角度q2d同时连带欠驱动杆到目标角度q1d时，系统末端点运动到目标坐标位置(xd,yd)。基于此思想，下面设计控制器实现平面Acrobot末端点的位置控制。

4 控制器设计

从上面分析可知，当控制驱动杆到达目标角度q2d时，欠驱动杆也将被连带控制达到目标角度q1d，从而实现系统的控制目标。本节将依据系统这一特性，通过为平面Acrobot系统构造李雅普诺夫函数来设计控制器，并针对控制器的设计参数，提出改进计划，实现系统末端点位置的快速控制。

(19)

其中，Fi(X)、Gi(X)是关于X的非线性函数，具体形式如下：

构造如下李雅普诺夫函数为

(20)

其中，x2d=q2d。

式(20)对时间求导得

(21)

即

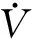
(22)

若设计

x2-x2d+F2(X)+G2(X)τ2=-rx4。

(23)

其中，r(r>0)为设计参数。

则将式(23)代入式(22)中有

(24)

因此，控制器可设计为

(25)

(26)

将式(25)或式(26)代入式(19)中可得到以下闭环系统为

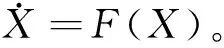
(27)

闭环系统式(27)的框图如图3所示。

图3 闭环系统(27)的框图Fig.3 Block diagram of closed system(27)

Φ={X∈R4|0≤V(X)≤C}。

(28)

其中C为正的常数。

系统式(27)任意始于Φ内的解X对于所有t≥0仍处于Φ。记Ψ为系统(27)的不变集，

(29)

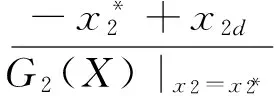
(30)

(31)

由LaSalle不变原理[23]可知，当t→，系统式(27)始于Φ内的解X趋于M，即：

因此，系统式(19)在控制器式(25)作用下可以运动并稳定到目标状态，即平面Acrobot系统末端点到达所设定的目标坐标位置(xd,yd)。

从图3可以看出，所设计控制器中包含1个PD控制器，其比例系数为1，微分时间参数为设计参数r(r>0)。当r较小时，e变化快(即x2变化快)，超调大；而当r较大时，e变化慢(即x2变化慢)，超调小。基于此想法，当第2杆角度x2与目标角度x2d偏差绝对值|e|较大时，调小r值，使e变化快；当|e|较小时，调大r值，防止系统超调。而且，为不影响系统的收敛性，应保证r>0。

基于上述思想，可将r设计成与驱动杆角度相关的一类非线性函数，即|x2d-x2|较大时，r取小；|x2d-x2|较小时，r取大。这里以分段函数和高斯函数为例进行说明。

1)r为分段函数，如下式所示：

(32)

其中：ed、rmax和rmin(rmax>rmin)为正的常数。

式(32)的函数图形如图4所示。

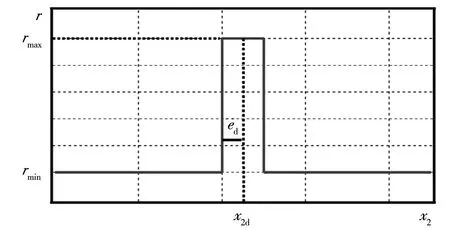
图4 分段函数Fig.4 Piecewise function

由图4可知，当x2离目标角度x2d较远时，r=rmin；当x2离目标角度x2d较近时，r=rmax。并且r一直处于正值，不影响系统式(27)的稳定性。那么控制器式(25)变为：

(33)

2)r为高斯函数，如下式所示：

(34)

其中A和σ都是正的常数。

式(34)的函数图形如下

图5 高斯函数Fig.5 Gauss function

由图5可知，当第2杆角度x2离目标角度x2d较远时，采用较小的r；而随着第2杆角度x2接近目标角度x2d时，r也随之增大。并且r一直处于正值，不影响系统式(27)的稳定性。因此控制器式(25)变为

(35)

5 仿真结果

按照上述设计方案，利用Matlab环境下的SIMULINK平台搭建系统仿真模型，完成平面Acrobot系统仿真控制。平面Acrobot系统的仿真参数如表1所示。

表1 平面Acrobot系统的仿真参数Table 1 Simulation parameter of plannar Acrobot system

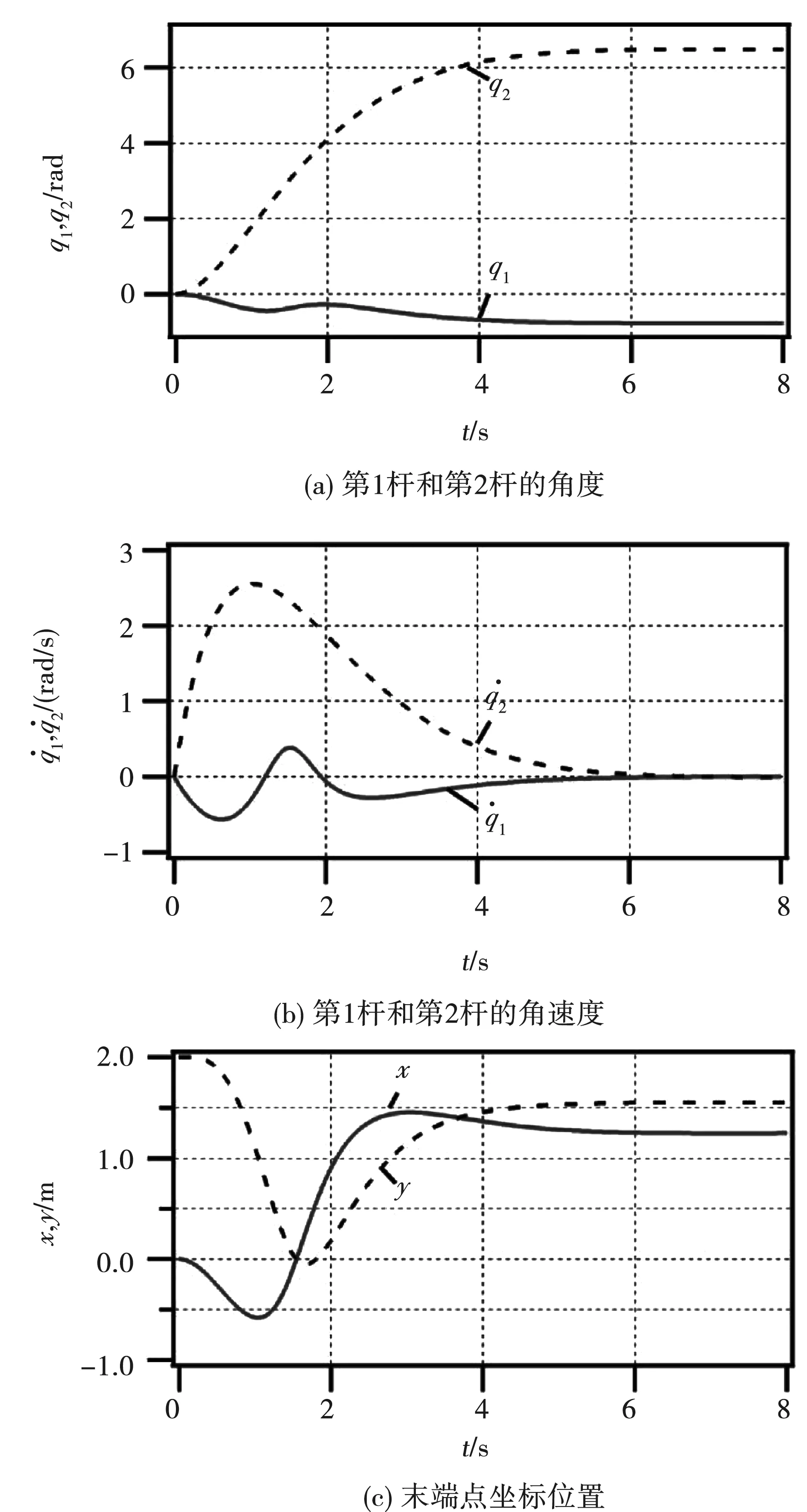
图6 r为常数时的仿真结果(r=1.8)Fig.6 Simulation results when r is a constant

1)r为常数，仿真结果如图6所示。

从图6(a)可看出，两杆均达到目标角度；从图6(c)可看出，系统末端点在6 s时已经达到所设计的目标坐标位置，说明所设计的控制器有效。

2)r为分段函数，仿真结果如图7所示。

从图7(a)可看出，两杆均达到目标角度；从图7(c)可看出系统末端点在2.7 s时已经达到目标位置(1.25,1.55)。说明所设计的控制器不仅有效，而且可缩短控制系统达到目标的时间。

3)r为高斯函数，仿真结果如图8所示。

图8 r为高斯函数时的仿真结果(A=60,σ=1)Fig.8 Simulation results when r is a gauss function

从图8(a)可看出，两杆均达到目标角度；从图8(c)可看出系统末端点在2 s时已经达到目标位置(1.25,1.55)。同样说明，所设计的控制器不仅有效，并且可缩短控制系统达到目标的时间。

因此，所设计的控制器不但能够完成系统末端点的位置控制任务，而且当将控制器的设计参数r设计成分段函数或者高斯函数这一类非线性函数时，可以较大地减少控制系统末端点到达目标坐标位置的时间。

6 结 论

为实现平面Acrobot系统末端点从初始位置到目标位置的快速控制，本文提出了一种基于可变设计参数的控制方法。该方法利用平面Acrobot系统的完全可积性质，通过控制驱动杆实现了欠驱动杆的连带控制。并根据平面Acrobot系统的两类约束关系定义目标函数，由PSO算法解出两杆目标角度值。最后通过构造李雅普诺夫函数来设计控制器，实现了平面Acrobot末端点的位置控制任务。特别是根据控制器中设计参数r的特性，将r设计成与驱动杆角度相关的一类非线性函数，实现了系统末端点位置的快速控制。仿真结果的对比验证了所提控制方法可以较大地减少系统到达控制目标的时间。

[1] LAI X Z,PAN C Z,WU M,et al.Unified control of n-link underactuated manipulator with single passive joint:A reduced order approach[J].Mechanism and Machine Theory,2012,56(12):170.

[2] 张静,孙强,关婷婷.TORA系统的自适应神经网络输出反馈控制[J].哈尔滨理工大学学报,2015,20(6):83.ZHANG Jing,SUN Qiang,GUAN Tingting.Output feedback control of the TORA system based on adaptive neural network[J].Journal of Harbin University of Science and Technology,2015,20(6):83.

[3] 高丙团,陈宏钧,张晓华.欠驱动机械系统控制设计综述[J].电机与控制学报,2006,10(5):541.GAO Bingtuan,CHEN Hongjun,ZHANG Xiaohua.Control design for underactuated mechanical systems:a survey[J].Electric Machines and Control,2006,10(5):541.

[4] 刘殿通,易建强,谭民.不确定欠驱动非线性系统的模糊滑模控制[J].电机与控制学报,2003,7(3):215.LIU Diantong,YI Jianqiang,TAN Min.Fuzzy sliding mode control of uncertain underactuated nonlinear systems[J].Electric Machines and Control,2003,7(3):215.

[5] LAI X Z,ZHANG A C,SHE J H,et al.Motion control of underactuated three-link gymnast robot based on combination of energy and posture[J].IET Control Theory and Application,2011,5(13):1484.

[6] 武俊峰,王胜达.模糊控制在二级倒立摆系统中的应用[J].哈尔滨理工大学学报,2013,18(4):12.WU Junfeng,WANG Shengda.The application of fuzzy control in double inverted pendulum[J].Journal of Harbin University of Science and Technology,2013,18(4):12.

[7] XIN X,SHE J H,YAMASAKI T,et al.Swing-up control based on virtual composite links for n-link underactuated robot with passive first joint[J].Automatica,2009,45(9):1986.

[8] ZHANG M J,TARNTJ.Hybrid control of the pendubot[J].IEEE/ASME Transactions on Mechatronics,2002,7(1):79.

[9] PATRICIO O J,OMAR S J,VIRGILIO L M.Toward a generalized sub-optimal control method of underactuated systems[J].Optimal Control Applications & Methods,2012,33(3):338.

[10] XIN X,MITAT,KANEDAM.The posture control of a two-link free flying acrobot with initial angular momentum[J].IEEE Transactions on Automatic Control,2004,49(7):1201.

[11] FANTONI I,LOZANOR,SPONG M W.Energy based control of the pendubot[J].IEEE Transactions on Automatic Control,2002,45(4):725.

[12] LAI X Z,PAN C Z,WU M,et al.Robust stabilization and disturbance attenuation for a class of underactuated mechanical systems[J].Journal of Central South University,2012,19(9):2488.

[13] MARTON L,HODEL A S,LANTOS B,et al.Underactuated robot control:comparing LQR,subspace stabilization,and combined error metric approaches[J].IEEE Transactions on Industrial Electronics,2008,55(10):3724.

[14] LUO Yibiao,LAI Xuzhi,WU Min.A positioning control strategy of planar Acrobot[C].Proceeding of the 30th Chinese Control Conference,Yantai,China,2011:743-747.

[15] SUZUKI T,MIYOSHI W,NAKAMURA Y.Control of 2R underactuated manipulator with friction[C].Proceedings of the 37th IEEE Conference on Decision and Control,Tampa,USA,1998,2007-2012.

[16] MAHINDRAKAR A D,SHODHAN R,BANAVAR R N.Point-to-point control of a 2R planar horizontalunderactuated manipulator[J].Mechanism and Machine Theory,2006,41(7):838.

[17] ARAIH,TACHIS.Position control of manipulator with passive joints using dynamic coupling[J].IEEE Transactions onRobotics and Automation,1991,7(4):528.

[18] POPESCU C,WANG Y,ROTH Z.Passivity based control of spring coupled underactuated horizontaldouble pendulum[C].Proceedings of the Florida Conference of recent Advances in Robotics,Florida,USA,2003:1-17.

[19] ALFREDO J R F,JAIME A G,Rafael C L.Trajectory planning and control of an underactuated planar2R manipulator[C].Proceedings of the IEEE International Conference on Control Applications,Mexico,2001:548-552.

[20] 刘庆波,余跃庆.基于遗传算法的欠驱动机器人模糊控制器设计[J].系统仿真学报,2008,20(8):2097.LIU Qingbo,YU Yuejin.Fuzzy controller design for underactuated robots based on GA method[J].Journal of System Simulation,2008,20(8):2097.

[21] ORIOLOG,NAKAMURAY.Control of mechanical systems with second-order nonholonomic constraints:Underactuated manipulators[C].Proceedings of 30th IEEE Conference on Decision and Control,Brighton,England,1991:2398-2403.

[22] CAO Shengqiang,LAI Xuzhi,WU Min.Motion control method of planar Acrobot based on trajectory characteristics[C].Proceeding of the 31th Chinese Control Conference,Hefei,China,2012:4910-4915.

[23] KHALIL H K.Nonlinear systems (3rd Ed.)[M].New Jersey:Prentice Hall,2002.

(编辑：张 楠)

RapidpositioncontrolapproachbasedonvariabledesignparameterforplanarAcrobot

WANG Ya-wu1,2，LAI Xu-zhi1,2，WU Min1,2

(1.School of Automation,China University of Geosciences,Wuhan 430074,China;2.Hubei key Laboratory of Advanced Control and Intelligent Automation for Complex Systems,Wuhan 430074,China)

A rapid position control approach based on a variable design parameter was presented for a planar Acrobot which has no gravity item.Firstly,angle constraint relationship and angular velocity constraint relationship between active joint and passive joint were obtained by employing the complete integral characteristics of the planar Acrobot.Next,another kind of the constraint relationship between the endpoint position and two angles of joint was deduced according to the physical structure of the planar Acrobot.Then,the target angles of joint were obtained by using particle swarm optimization (PSO) algorithm based on the above two kinds of constraint relationship.Finally,a controller was designed for planar Acrobot by constructing a Lyapunov function,and a variable design parameter of the controller was chosen to reduce the control time according to the characteristics of parameter.When the active link was controlled to the target angle,the passive link was also controlled jointly to its target angle by utilizing angular velocity constraint relationship and angle constraint relationship.That is,the endpoint of the planar Acrobot was driven to the target position.Simulation results demonstrate the effectiveness and rapidity of the proposed control approach.

planar underactuated mechanical system; planar Acrobot; position control; particle swarm optimization algorithm; nonlinear function

10.15938/j.emc.2017.09.015

TP 4

:A

:1007-449X(2017)09-0110-09

2015-01-20

国家自然科学基金(61374106)；湖北省自然科学基金(2015CFA010)；“111计划”项目(B17040)

王亚午(1990—)，男，博士研究生，研究方向为欠驱动机器人控制、非线性系统控制；赖旭芝(1966—)，女，教授，博士生导师，研究方向为智能控制、机器人控制和非线性系统控制；吴 敏(1963—)，男，教授，博士生导师，研究方向为鲁棒控制、智能控制和过程控制。

赖旭芝