混合转子无刷电励磁同步电机参数的解析计算

张凤阁，关涛，贾广隆，王皓

(沈阳工业大学 电气工程学院，辽宁 沈阳 110870)

混合转子无刷电励磁同步电机参数的解析计算

张凤阁，关涛，贾广隆，王皓

(沈阳工业大学 电气工程学院，辽宁 沈阳 110870)

研究了无刷电励磁同步电机的运行机理和混合转子的磁场调制原理，运用叠加法与绕组函数法相结合，建立了混合转子无刷电励磁同步电机电感参数模型，研究了混合转子无刷电励磁同步电机电感参数解析计算方法，通过编制程序对电机的电感参数进行计算，得出了电感参数随转子位置变化的规律，并采用有限元法计算了电机的电感参数。研制了实验样机，采用静测法进行了电感参数的测试。将解析计算结果分别与有限元计算结果和实验结果进行对比分析，验证了所提出混合转子无刷电励磁同步电机电感参数解析计算模型的正确性。为该种电机的进一步仿真分析与研究奠定了技术基础。

无刷；同步电机；混合转子；电感参数

0 引 言

无刷电励磁同步电机(brushless electrically excited synchronous machine,BEESM)是一种新型的电励磁同步电机，具有结构简单、无电刷和滑环装置、运行安全可靠以及功率因数可调等优点。

BEESM设计思想来源于传统电励磁同步电机和无刷双馈电机，其定子上嵌有两套不同极数的绕组，分别为2pp极的三相对称绕组和2pf极的单相励磁绕组，两套绕组是通过特殊转子使得两套组之间发生耦合的。该种电机的转子[1]分为笼型转子、凸极式磁阻转子和磁障式磁阻转子。笼型转子结构简单，起动性能好，但是磁场调制能力较弱以及转子上会产生铜耗。磁阻转子[2-6]一般有3种结构,分别为普通凸极转子、ALA转子和径向叠片磁阻转子。这3种磁阻转子调制效果最好的是径向叠片磁阻转子，但是该转子的起动性能较差。本文提出一种笼型转子和磁阻转子相结合的混合转子，该种转子同时具有较强的磁场调制能力、起动性能好以及制作工艺简单等特点。

BEESM结构上的特殊性，决定了该种电机的电磁关系比普通交流电机复杂得多，对其工作特性和性能分析相对困难，现有的分析方法还不能完全适用。分析电机动态性能和工作特性的基础是电机的电感参数，目前关于ALA转子、普通凸极转子和笼型转子电感参数计算已有研究[7]，但是对混合转子BEESM电感参数的计算并不适用。本文首先介绍了BEESM的结构特点和运行机理。其次根据混合转子的磁场调制原理，基于绕组函数和叠加原理推导了电机电感参数的解析计算方法。最后通过有限元法和样机实验，验证了电感参数计算模型的正确性。

1 混合转子无刷电励磁同步电机的结构原理

无刷电励磁同步电机的结构如图1所示。定子上同时嵌有两套绕组，一套为三相对称绕组，另一套为单相绕组。其中电枢绕组的极对数为pp，与电网直接相连，频率为fp；励磁绕组的极对数为pf，由直流电源供电，定子的实物如图2所示。BEESM的转子是对磁路进行限制，恒定的励磁磁场经过转子调制会产生与电枢磁场极数相同的磁场;因此定子两套绕组间产生了良好的电磁耦合。本文提出了隔磁磁障和短路笼条相结合的混合转子结构，该种转子主要构成为：在径向叠片磁阻转子铁心中加入磁层，并在构成的磁障式转子中加入短路笼条，两个端部分别短路连接，便构成了隔磁磁障和短路笼条相结合的混合转子。由于磁障可在冲制转子槽型时同时加工出来，没有增加太多的复杂性;而且通过在径向磁障转子中加入笼条，对电机中的磁路的限制更加完善，进而增加了转子的磁场调制能力，同时由于转子中加入了笼条，使得电机的起动性能较径向磁障转子有所提高。因此，该种转子具有结构简单、损耗较小，起动性能和动态性能好的优点，非常适合推广应用。混合转子结构及实物如图3所示。

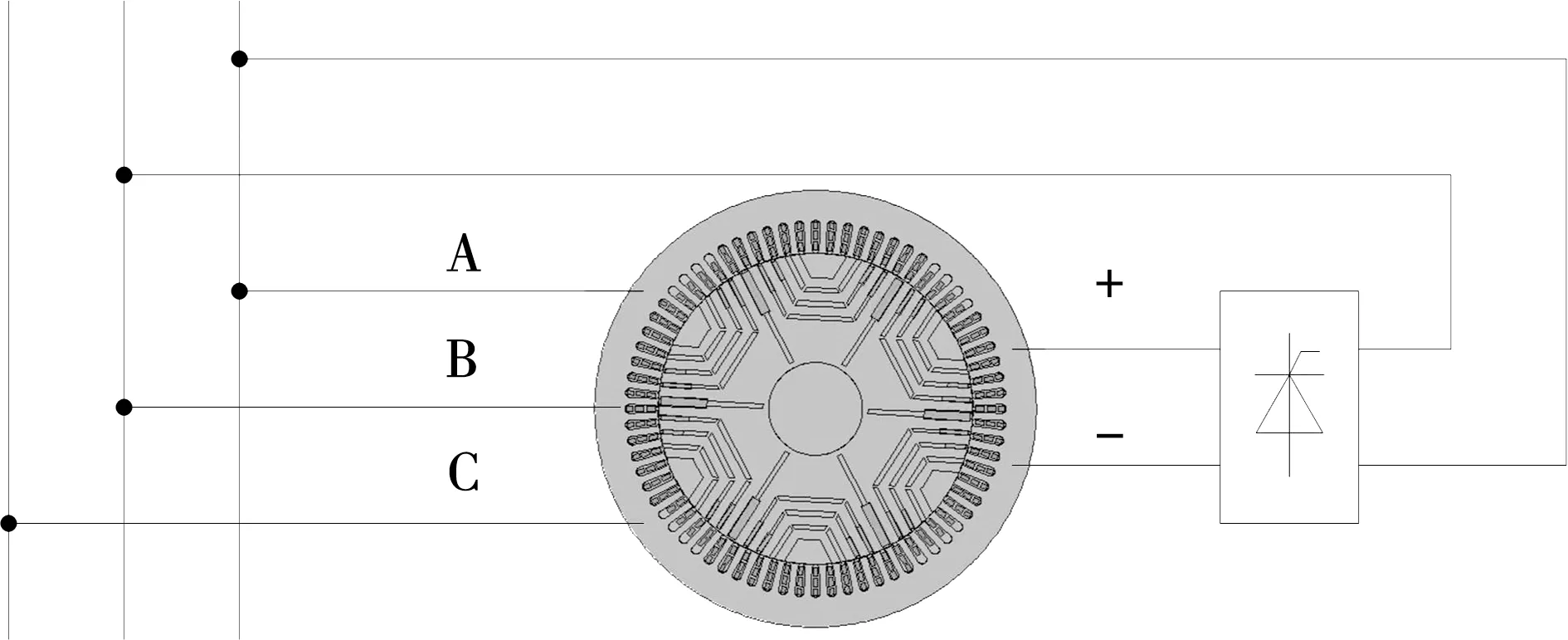
图1 BEESM的结构图Fig.1 Structure of BEESM

图2 BEESM的定子图Fig.2 Stator of BEESM

BEESM运行方式有两种，分别为电动状态和发电状态。传统电励磁同步电机起动一般分为辅助电机起动法，变频起动和异步起动法[8]。当BEESM作为电动机运行时，其运行方式与异步起动电励磁同步电机的运行方式相似。起动前先把附加电阻与励磁绕组相连，然后用异步电动机直接起动的方法将电枢绕组投入电网，依靠异步转矩起动加速转子使之接近同步转速nr，其计算式为

(1)

再加入直流励磁电流，依靠同步转矩将转子牵入同步，通过调节励磁电流改变电机的功率因数。当作为发电机运行时，BEESM被原动机拖动到同步速度nr，励磁绕组中通入直流励磁电流，发电的电枢绕组与负载相连，通过调节励磁电流维持端电压的恒定。

图3 混合转子结构Fig.3 Hybrid rotor structure

2 混合转子无刷电励磁同步电机电感参数的解析计算

电机参数是建立电机数学模型的基础，电机的性能主要取决于电机两套绕组之间的互感参数;因此，电感参数的计算就显得非常重要，但BEESM复杂的磁场使电感参数的计算显得比较困难。

混合转子BEESM结构上的复杂性使BEESM的电感参数与转子位置角的关系并没有传统电励磁同步电机那样直观，因此有必要研究其电感参数的计算方法。

2.1 绕组函数

用于电感参数计算的绕组函数法通用性比较强，特别适用于非常规电机结构。绕组函数的物理意义为：当电机某相绕组通入单位电流时，沿着电机气隙的磁动势分布亦反映了绕组匝数的空间分布规律。电机中每相绕组的磁动势可用其绕组函数和相电流的乘积来表示[9]。

任意两套绕组(如第i和第j个绕组)之间的互感计算公式为

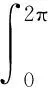
(2)

式中：r和l分别代表电机定子内圆半径和铁心长；φ为沿圆周的位置坐标；θr为电机转子轴线与定子轴线之间的机械角度；g-1(θr,φ)为气隙函数；μ0为空气的磁导率；Ni(θr,φ)和Nj(θr,φ)分别为第i(i=1,2,3,4)个绕组的绕组函数和第j(j=1,2,3,4)个绕组的绕组函数，并且由于在定子上，则绕组函数仅与φ有关。

为了简化计算，在计算中做了如下假定：a)忽略铁心磁压降；b)用卡氏系数考虑开槽对气隙磁导的影响。

2.2 求解模型的建立

混合转子BEESM电感参数的计算，无论用基于磁路的概念，还是基于网格剖分的磁场计算法，都很困难[10]。为此，本文提出了混合转子BEESM电感参数的解析计算方法。

本文采用绕组函数法对电机的电感参数进行计算。根据各自的绕组排列求出绕组函数，而电机的磁路是通过气隙函数g-1(θr,φ)确定。用叠加法将磁障转子及笼型转子的影响进行叠加。电感参数计算的具体步骤为：首先，计算每个导磁层对四相绕组电感参数的“贡献”，将所有导磁层的“贡献”叠加; 然后，再将短路笼条的“贡献”进行叠加，本文提出将笼条的影响通过气隙比磁导的形式加以考虑[11]; 最后，减去笼条的漏感，进而求得绕组的电感参数。该方法可较好地解决混合转子无刷电励磁同步电机电感参数计算的难题。

笼型转子是通过磁动势谐波的磁场调制作用实现两套定子绕组间的耦合的。由于不穿过短路笼条，定子磁场沿d轴方向很容易进入转子。沿d轴电机气隙比磁导为μ0/g0，其中g0为定转子之间的气隙长。由于穿过所有短路笼条，定子磁场沿q轴方向将要受到各转子短路笼条中感生电流产生的相反方向磁通强烈抵制，很难进入转子。理想情况下该方向的电机气隙的等效比磁导为0。在d轴和q轴之间定子磁通进入转子所受的阻力随所穿越短路笼条数逐级增加。图4为笼型转子展开图及等效气隙磁导波形。

磁障转子是通过磁导谐波的磁场调制作用实现两套定子绕组间的耦合的。定子磁通通过齿顶进入转子，因为齿顶部分的磁阻小，磁障转子齿顶的气隙比磁导为μ0/g0。由于通过齿间部分磁阻很大，定子磁通很难进入转子，理想情况下该部分的电机气隙的等效比磁导为0。图5为磁障转子展开图及气隙磁导波形。

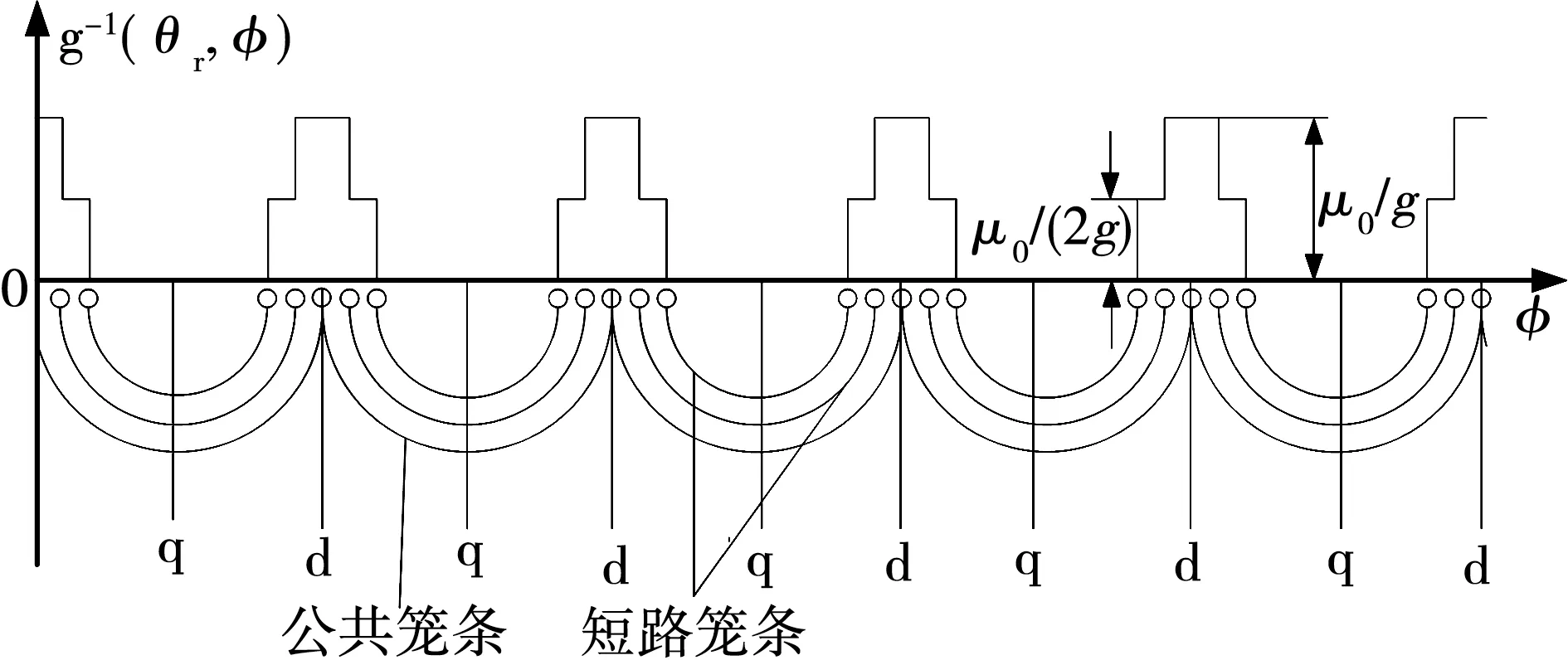
图4 笼型转子展开图及气隙磁导波形Fig.4 Cage rotor expansion graph and the gap magnetic waveform

图5 磁障转子展开图及气隙磁导波形Fig.5 Magnetic barrier rotor expansion graph and the gap magnetic waveform

混合转子的气隙比磁导函数是将笼条的气隙比磁导函数与磁障转子的气隙比磁导函数进行叠加而来，图6为混合转子的展开图及气隙磁导波形。理想情况下非导磁部分(齿间)的电机气隙的等效比磁导为0。对于导磁部分，定子磁场沿d轴方向很容易进入转子，因为该处的气隙磁导值最大，其值为2μ0/g0。沿q轴方向定子磁通最不容易进入转子，因为磁通不仅要穿过所有的转子短路线圈，而且还穿过了非导磁部分，理想情况下该方向的电机气隙的等效比磁导为μ0/g0。d轴和q轴之间定子磁通进入转子所受的阻力随所穿越短路笼条数逐级增加。

假设各个导磁层的厚度相等，且每组导磁层个数为Nr，则非导磁层个数为Nr-1。磁障厚度为t2，定子内径为Di，则导磁层厚度为

(3)

式中：αp为极弧系数；pr为转子极对数。假定图6中任何一个导磁层均具有理想的气隙比磁导函数(忽略边缘效应)，其数学表达式为：

(4)

式中kg为波形系数。其中几个关键点坐标为：

(5)

式中kr=1,2,3,…,Nr。

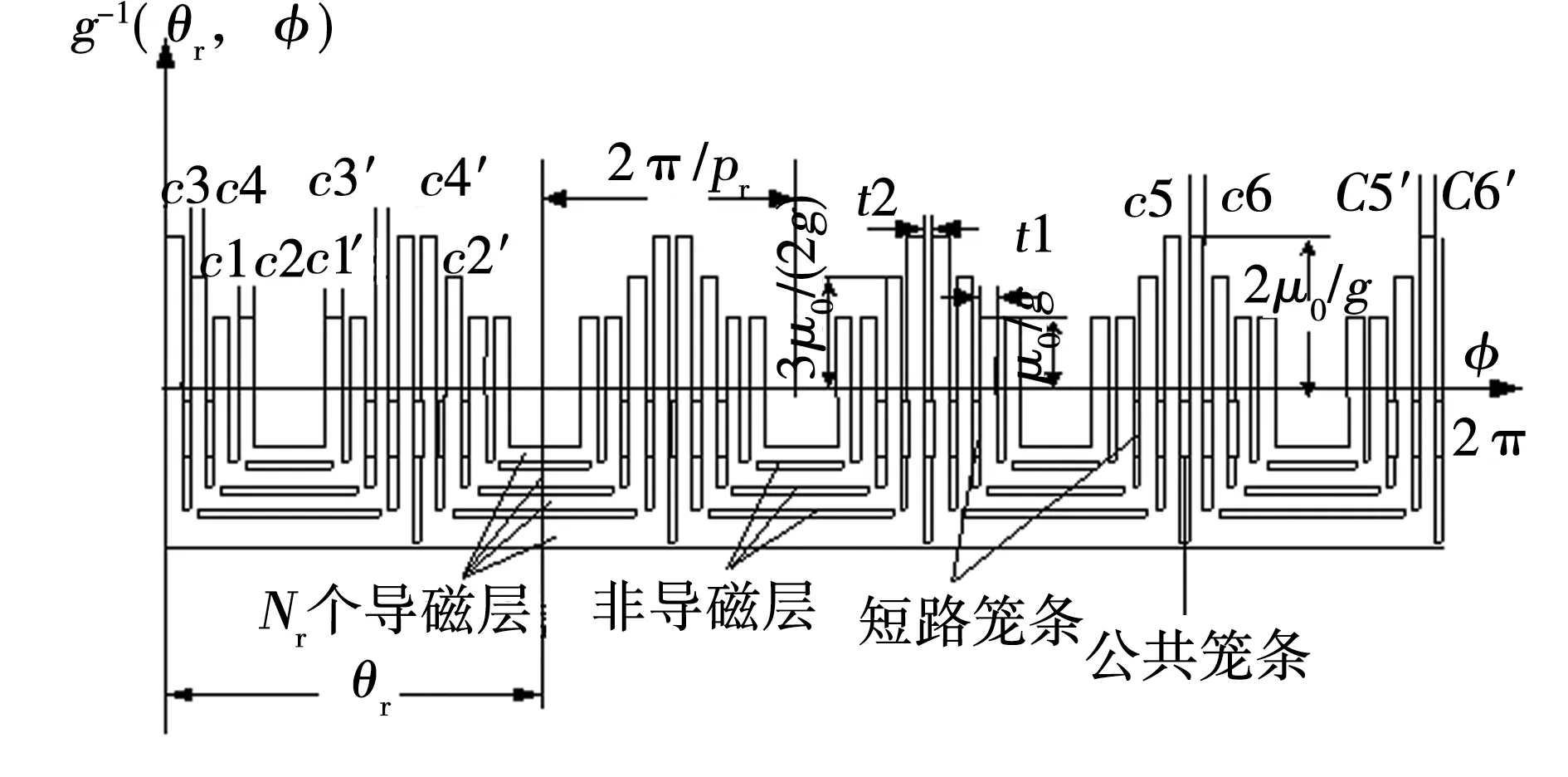
图6 混合转子展开图及气隙磁导波形Fig.6 Hybrid rotor expansion graph and the gap magnetic waveform

参照式(2)，求出单个导磁层对i相绕组与j相绕组之间互感的贡献为

(6)

将所有导磁层的“贡献”叠加，求出所有导磁层对i相绕组与j相绕组之间互感的贡献。由于混合转子中的笼条会有漏感产生，即给“贡献”打了个折扣。接下来计算转子漏感,电机中笼条的连接方式如图7所示。

转子漏感主要包括槽漏感和端部漏感,电机转子的槽如图8所示。

槽漏感的计算式为

(7)

式中：λs2为转子的总漏磁导；kσ2为漏感系数；q2为每极每相槽数。

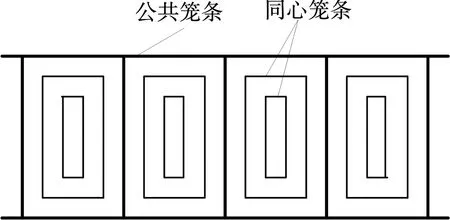
图7 笼条的连接方式Fig.7 Connection mode of cage bar

图8 转子槽型图Fig.8 Rotor slot type

电机转子的总漏磁导

λs2=λL2+λU2+λt2+λE。

(8)

式中：λL2为槽比漏磁导；λU2为槽口比漏磁导；λt2齿顶比漏磁导；λE为端部槽比漏磁导。

槽比漏磁导为

(9)

槽口比漏磁导为

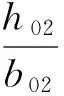
(10)

齿顶比漏磁导为

λt2=10/(7+18b02/δ)。

(11)

端部槽比漏磁导

(12)

式中：DR为转子外径；Z2p为转子每极槽数；l′为导条伸出铁心的长度(两端)。

电机的漏磁系数为

kσ2=2μ0(2prN2)2/pr。

(13)

最后，基于式(7)得出电感的计算式为

Lij=Lij(θr)-Ls2。

(14)

2.3 电感参数的计算

基于上述混合转子电感参数的求解模型，对表1给出的8+4极混合转子BEESM的电感参数进行编程计算。图9为电感随转子位置变化的曲线。

表1 样机主要参数Table 1 Main parameters of the prototype

由图9可知两套绕组之间的互感周期与转子等效极数pr相同，其峰值为84 mH，电枢绕组自感为42 mH，电枢绕组各相之间的互感为-19.5 mH。

图9 电机绕组的电感值随转子位置变化的曲线Fig.9 Curve of inductance value of the windings with the rotor position change

3 有限元法计算电机的电感参数

为了验证电感参数解析算法的准确性，采用有限元法计算电机的电感参数。首先，对电机进行建模，有限元模型如图10所示(样机的基本数据详见表1)。

图10 BEESM的有限元模型Fig.10 Finite element model of BEESM

然后对求解域的边界、定子绕组、电机转速和材料进行设置，其中励磁绕组通入直流电、功率绕组开路且电机以自然同步速度转动。最后计算出电机的动态电感，得出电机的电感随转子位置变化的曲线，如图11所示，两套绕组之间互感的峰值为75 mH，电枢绕组自感为37.5 mH，电枢绕组各相之间的互感为-17 mH。

图11 有限元分析结果Fig.11 Calculated values of the inductance parameters with the finite element analysis of BEESM

4 实验验证

4.1实验方法

本文采用“静测法[12]” 对BEESM样机的电感参数进行测量，BEESM的实验平台如图12所示。

图12 无刷电励磁同步电机的实验图Fig.12 experiment chart of BEESM

首先，仅在第j相绕中通入频率为f的正旋交流电，而其他绕组开路。然后，测得转子在不同位置时通电相的电流和其它各相的电压值。最后，不同转子位置下的电机的电感参数为：

(15)

式中：Uk为开路相的电压值；Uj为通电相的电压值；Ij为通电相的电流值；ω为通入正弦电流的角频率；Ljj为通电相的自感；Lkj为通电相与开路相之间的互感。

4.2 实验研究

采用上述方法对一台8+4极混合转子BEESM进行了测试。实验时给励磁绕组通入55 V，50 Hz的交流电，电枢绕组各相互相断开，转子每旋转2°测量电枢绕组的反电势和励磁绕组电流，根据式(15)计算出电机的电感参数，如图13所示。可知两套绕组之间的互感峰值为82 mH，电枢绕组自感为40 mH，电枢绕组各相之间的互感为-20 mH。

基于实验测得的电感参数得出混合转子BEESM的电感参数解析计算结果如表2所示。可以看出，解析计算结果与二维有限元法和实验结果基本一致，但还是存在一定的误差。解析法产生误差的主要原因是计算电机的参数时为了简化计算忽略了铁磁材料饱和以及高次谐波对电机参数的影响，而有限元法产生误差的主要原因则是计算时忽略了电机的端部漏感以及剖分网格大小对计算电感参数的影像。同时根据表2数据可知，解析计算的方法可以较为准确地对该种电机的电感参数进行计算。

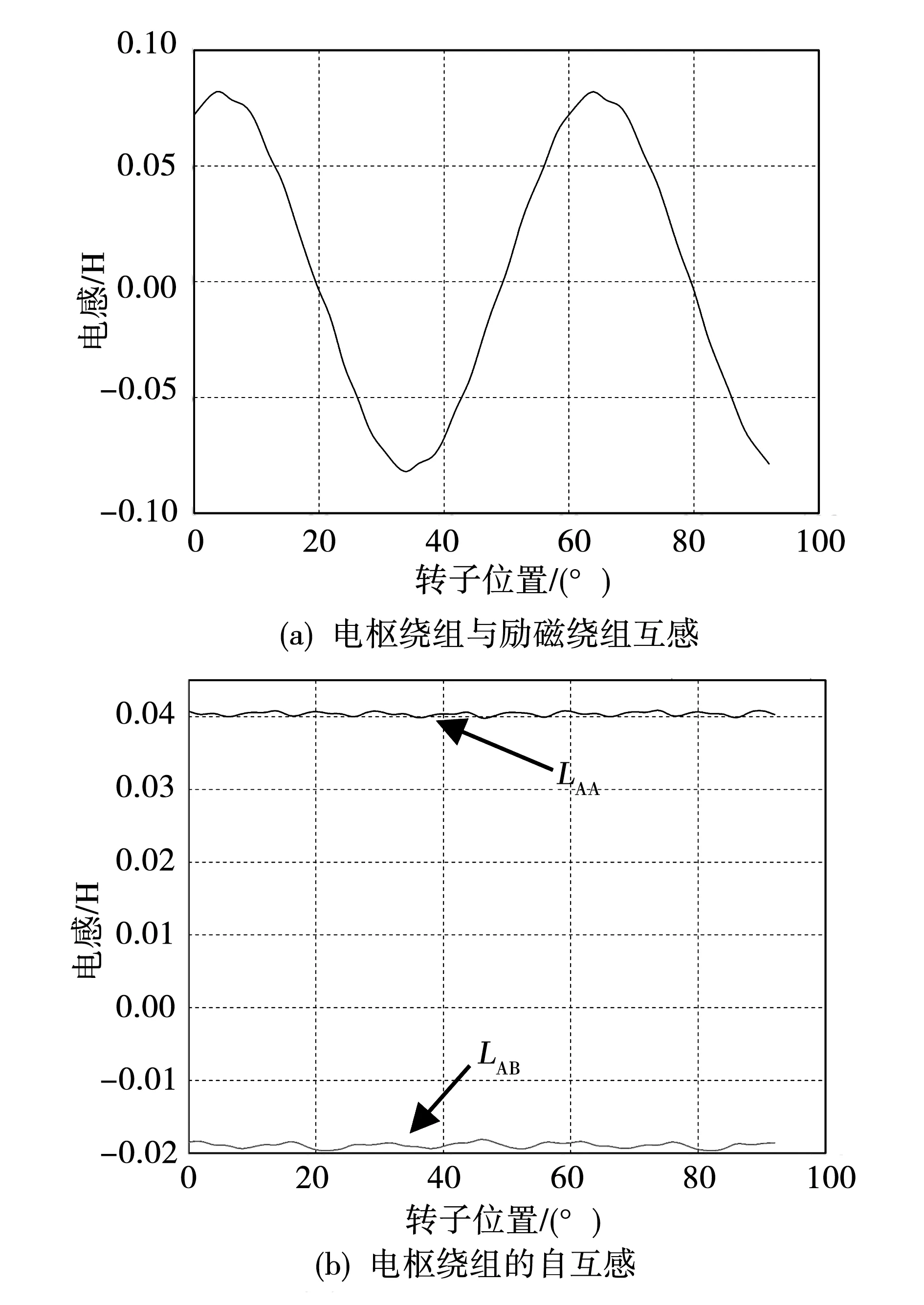
图13 实验结果Fig.13 Measured values of inductance parameters of BEESM

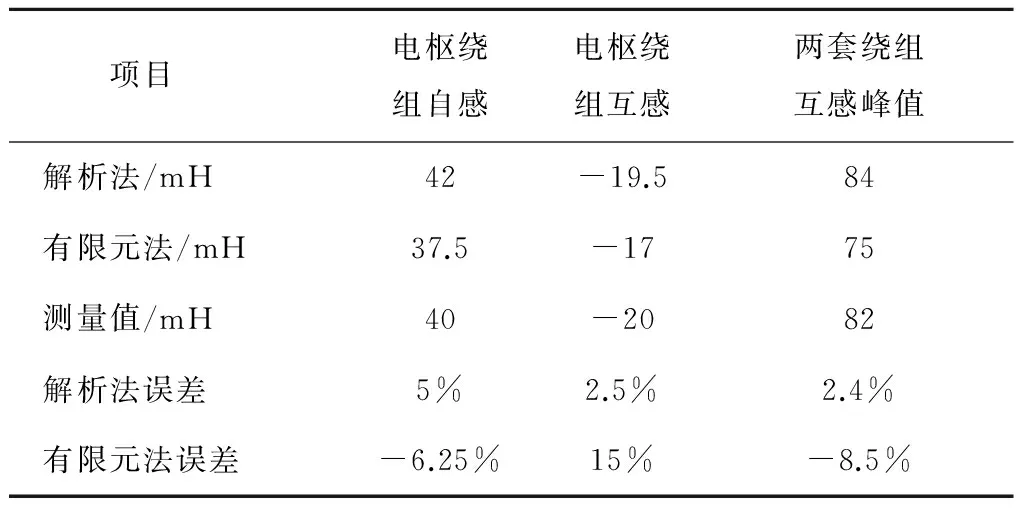
表2 电感参数计算结果Table 2 Result of calculation of inductance parameters

4 结 论

本文提出了混合转子BEESM电感参数的解析计算方法。为提高计算精度，该方法不仅考虑了笼条对磁场的影响，而且考虑了笼条的漏感。另外本文还采用了实验方法和有限元方法对电机的电感参数进行了测量与计算。从电感参数计算方法所计算的结果与实验值和有限元的结果进行对比分析，证明了本文所提出电感参数计算方法的正确性。

[1] 韩力,高强,罗辞勇,等.不同转子结构无刷双馈电机的运行特性对比[J].电机与控制学报,2010,14(3):6.HAN Li,GAO Qiang,LUO Ciyong,et al.Comparasion on the performance of brushless doubly-fed machine with different rotor structures [J].Electric Machines and Control,2010,14(3):6.

[2] 张岳,王凤翔,邢军强.磁障转子无刷双馈电机[J].电工技术学报,2012,27(7):49.ZHANG Yue,WANG Fengxiang,XING Junqiang.Brushless doubly-fed machines with magnetic barrier rotor[J].Transactions of China Electrotechnical Society,2012,27(7):49.

[3] XU L,TANG Y,YE L.Comparison study of rotor structures of doubly excited brushless reluctance machine by finite element analysis[J].IEEE Transactions on Energy Conversion,1994,9(1):165.

[4] KNIGHT A M,BETZ R E,DORRELL D G.Design and analysis of brushless doubly fed reluctance machines [J].IEEE Transactions on Industry Applications,2013,49(1):50.

[5] KNIGHT A M,BETZ R E,DORRELL D.Design principles for brushless doubly fed reluctance machines[C]//37thAnnual Conference of IEEE Industrial Electronics Society,2011:3602-3607.

[6] 刘慧娟.一种径向叠片磁障式转子双馈无刷电机的设计与性能分析[J].电工技术学报,2012,27(7):55.LIU Huijuan.Design and performance analysis of a doubly excited brushless machine with adially laminated magnetic barrier rotor[J].Transactions of China Electrotechnical Society,2012,27(7):55.

[7] 张凤阁.磁场调制式无刷双馈电机研究[D].沈阳:沈阳工业大学,1999.

[8] 汤晓燕,郭芳.凸极同步电动机的牵入同步[J].电机与控制学报,2004,7(4):272.TANG Xiaoyan,GUO Fang.The pulling into step of a salient-pole synchronous motor[J].Electric Machines and Control,2004,7(4):272．

[9] 王凤翔,张凤阁.磁场调制式无刷双馈交流电机[M].吉林：吉林大学出版社,2004.

[10] 赵争鸣.新型同步磁阻永磁电机发展及现状[J].电工电能新技术,1998,17(3):22.ZHAO Zhengming.Development and current situation of new type machine of synchronous reluctance permanent magnet machine [J].Advanced Technology of Electrical Engineering and Energy,1998,17(3):22.

[11] GONG Sheng,YANG Xiangyu,JI Liangzhou.Inductance calculation for stator winding of brushless doubly-fed machine[C]//2010 International Conference on Electrical and Control Engineering,2010:3834-3837.

[12] 潘再平,章玮.无刷双馈风力发电机的理论分析[J].新能源,2000,22(7):1.PAN Zaiping.ZHANG Wei.Theoretical analysis of brushless doubly fed wind power generator[J].New Energy,2000,22(7):1.

(编辑：刘琳琳)

Analyticalcalculationofparameterofbrushlesselectricallyexcitedsynchronousmachinewithhybridrotor

ZHANG Feng-ge，GUAN Tao，JIA Guang-long，WANG Hao

(School of Electrical Engineering,Shenyang University of Technology,Shenyang 110870,China)

The operating principle of brushless electrically excited synchronous machine(BEESM) and field modulation principle of hybrid were studied.The inductance parameter model of BEESM with hybrid rotor was established by combining the superposition method and the winding function method.The analytical calculation method of inductance parameters of BEESM with hybrid rotor was studied.The variation of inductance parameters with the rotor position was obtained by programming calculation,and the inductance parameters of BEESM were calculated by the finite element method.A prototype machine was manufactured,inductance parameters of machine was measured by method of static test.The analytical results are compared with the finite element results and the experimental results respectively,and the correctness of calculation method of inductance parameter is verified.It lays theoretical basis for further simulation and analysis of this kind of machine.

brushless; synchronous machine; hybrid rotor; inductance parameter

10.15938/j.emc.2017.09.005

TM 352

:A

:1007-449X(2017)09-0031-07

2016-04-27

国家自然科学基金重点资助项目 (51537007)；国家自然科学基金(51277125)

张凤阁(1963—)，男，教授，博士生导师，研究方向为特种电机及其控制；关 涛(1992—)，男，硕士研究生，研究方向为电机及其控制技术；贾广隆(1987—)，男，博士研究生，研究方向为特种电机及控制；王 皓(1990—)，男，硕士研究生，研究方向为电机与电器。

关 涛