基于优化权重的卡尔曼滤波与无偏灰色组合模型的短期负荷预测

林天祥 张 宁 胡 军

（1. 福州大学电气工程与自动化学院，福州 350116；2. 山西漳泽电力股份有限公司，太原 030006）

基于优化权重的卡尔曼滤波与无偏灰色组合模型的短期负荷预测

林天祥1张 宁1胡 军2

（1. 福州大学电气工程与自动化学院，福州 350116；2. 山西漳泽电力股份有限公司，太原 030006）

本文针对短期负荷预测动态、随机的特点，提出了一种基于优化权重的卡尔曼滤波与无偏灰色组合预测模型。该模型充分发挥了卡尔曼滤波准确估计动态系统的优势，并合理利用无偏灰色模型挖掘随机数据潜在规律的特点。首先根据卡尔曼滤波预测中出现特殊日收敛不足的缺陷，利用趋势稳定，规律性强，消除固有偏差的无偏灰色理论加以弥补。根据无偏灰色理论趋势稳定向上，在短期负荷预测中某些下降趋势数据点误差较大的缺陷，利用卡尔曼滤波依据大量数据最优估计的平均思想加以弥补。并且采用线性组合法进行结合进一步规避了预测风险。算例结果表明，该预测模型精度较高，具有实用性。

卡尔曼滤波模型；无偏灰色模型；短期负荷预测；组合预测

短期负荷预测在电力系统的电能调度、经济规划及安全运行方面起重要作用。短期负荷预测受天气、节假日、政策等方面的影响，呈现动态、随机、趋势上升的特点。长期研究以来，经过不断革新与探索，更多创新的理论与算法应用于负荷预测，预测精度愈趋精准，如专家系统法[1-2]、神经网络法[3-4]、回归分析法[5-6]、支持向量机[7]、灰色系统理论法等。这些方法都取得了不错的预测效果。

无偏灰色理论模型是白指数律重合性的灰色模型，具有线性变换一致性[8]。无偏灰色理论模型[9]不但具有灰色理论固有的所需数据少、规律性强、预测精度高的特点，而且能充分利用原始序列第一点信息，有效地对预测值进行修正，消除灰色理论固有的偏差。该模型适用于线性与非线性预测，应用范围广。

卡尔曼滤波[10]是一种基于最小均方差递归滤波的最优估计算法。通过一系列包含噪声的测量中，估计动态系统的状态。卡尔曼滤波是用状态空间表示的系统，存在外部变量的自回归移动平均系统（ARMAX）或可用有理传递函数表示的系统均可转换为卡尔曼滤波计算。大部分短期日电力负荷即可认作是存在各种各样外部变量的自回归移动平均系统。通过国内外学者对卡尔曼滤波的研究[11-12]，可以发现卡尔曼滤波能有效纠正人为或是测量中的伪数据，剔除干扰，使预测趋于真实值。

据此，本文提出了卡尔曼滤波与无偏灰色GM(1,1)的优化权重组合模型。卡尔曼滤波不假设数据和噪声都是相对平稳的过程。对于每个时刻的系统扰动和观测误差，只要对它们的相似性质作相当的设定，并且处理含有噪声扰动的观测信号，就能求得误差为最小的真实信号的估计值。但是存一些特殊日负荷的情况，卡尔曼滤波会在平均的意义上作出误差偏大的估计，而无偏灰色负荷预测模型不考虑平均意义，不考虑分布因素，预测趋势稳定并且可在较少的数据量中得出存在潜在规律且精度较高的预测值，在处理特殊日负荷值上有一定优势，能弥补卡尔曼滤波的不足。不过在短期负荷预测中无偏灰色模型存在利用数据过少，预测值趋势稳定递增的缺点，而卡尔曼滤波模型的数据修正、跟踪的特性可弥补无偏灰色模型的缺点。由上可知，两种算法存在互补性，并在算例中也得到了证实。

1 无偏灰色理论模型

设原始数据序列为X(0)=(x(0)(1), x(0)(2), …, x(0)(n))。X(0)1-AGO累加序列为，其中

无偏灰色模型用传统灰色模型中的参数列表示原始序列中的a和A，使传统灰色理论固有偏差被消除，提高了模型的精度与适用范围。而无偏灰色模型存在对动态系统预测估计不足，变化趋势慢，信息更新差的缺陷。

2 卡尔曼滤波模型

1960年Kalman提出了卡尔曼滤波理论，卡尔曼滤波由观测方程与状态方程组成，由状态方程的递推性，采用无偏最小均方差估计的方式，结合递推算法对状态方程的最佳估计，从而得到过滤噪声后的最佳预测值。量测值重新构建状态方程是卡尔曼滤波的本质。卡尔曼滤波以“预测—实测—修正”的顺序递推，根据系统的量测值来消除随机噪声，从被干扰的系统中恢复系统的真实情况。卡尔曼滤波的基本思想是采用数据与噪声的状态向量模型，用前一时刻的估算值和此时的观测值来更新状态变量，并且求出此时的估算值。卡尔曼滤波适合于实时修正预测，通常采用计算机运算。

由线性时间离散系统[13]为

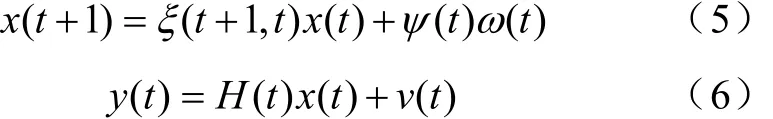
式中，x为n维状态变量，(1,)ttξ+为nn×的状态转移矩阵，()tψ为nr×的输入噪声转移矩阵，()tω为p维输入噪声；()yt为m维测量向量，()Ht为mn×维的测量矩阵，()vt为m维的测量噪声。

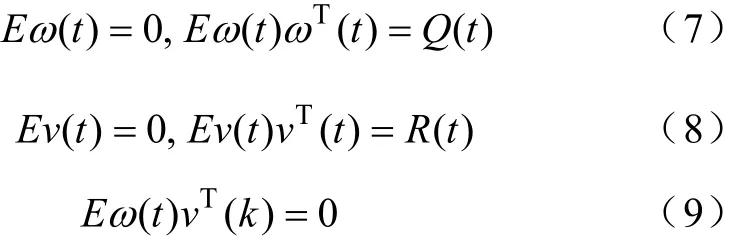
输入噪声()tω与测量噪声()vt是互不相干、均值为0的独立白噪声，其特性为式中，E表示为数学期望；p×p阶输入噪声协方差阵Q(t)是对称且正定的；m×m阶测量噪声协方差阵R(t)是对称且正定的。初始x(0)独立于ω(t)和v(t)，并且

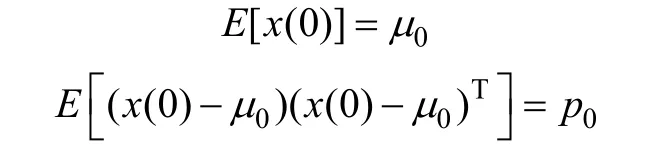
记xˆ(t+1|t)为(t+1)时的x(t+1)的估计值。设求得x(t)的最优滤波估计为xˆ(t)。在时刻(t+1)获取测量值之前ω(t)不可预测。因此用式

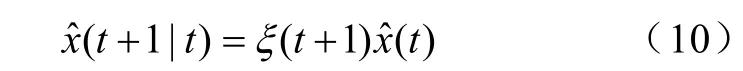
作x(k+1)的先验估计。测量值y(t+1)的预测为yˆ(t+1)=H(t+1)xˆ(t+1|t )估计值xˆ(t+1|t)是存在误差的。其误差的协方差为

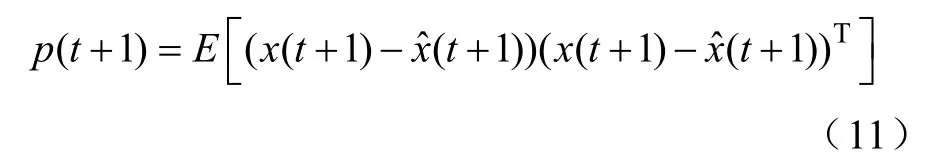
需要y(t+1)与H(t+1)xˆ(t+1|t)的差修正。以获得最优滤波估计。为此在(y(t+1)−H(t+1)xˆ(t+1|t))乘以K(t+1)可以得到

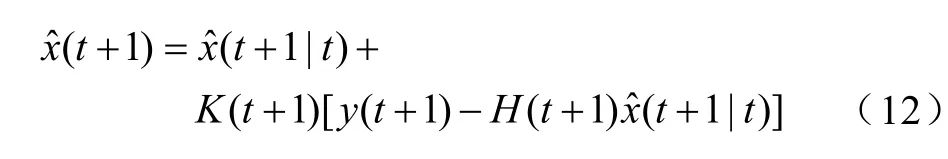
式中，K为卡尔曼增益，且满足Tr[P(t+1)]=min。可得

最终可得卡尔曼滤波的递推方程组为

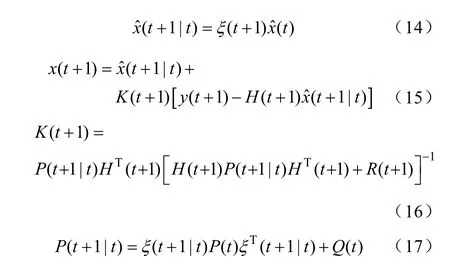
预测连续几日的同时刻负荷值，通常可以作下式：

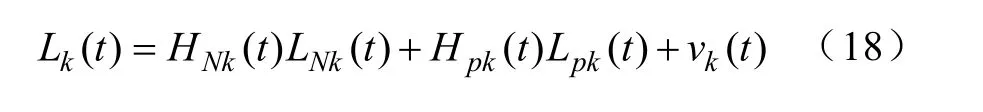
式中，Lk(t)为第t天k时刻的负荷值LNk(t)为该时刻的基本负荷；pk为前一天的该时刻的负荷值；为参数矩阵。

应用尔曼滤波进行状态预测，作如下变换：

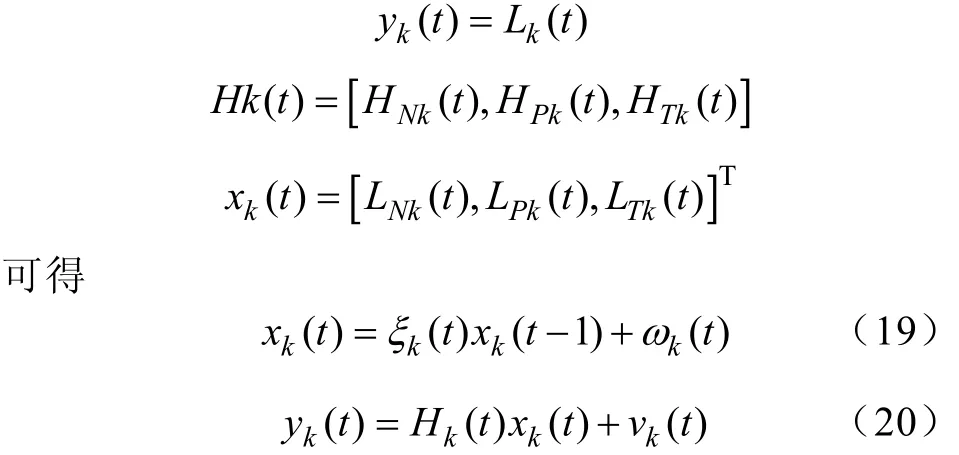
将式（19）和式（20）与卡尔曼滤波递推式（14）至式（17），即构成卡尔曼滤波短期负荷预测的模型。

3 组合模型

卡尔曼滤波是一个适用于线性、离散和有限维系统的算法。卡尔曼滤波是以最小均方误差为估计的最佳准则，进行协方差递归估算，不断估算后求得最优的预测值。无偏灰色理论挖掘数据潜在规律，建立累加模型，弱化数据随机性，并且消除了灰色理论固有偏差进行负荷预测，同样也适用于线性、非线性、离散和有限维系统。这是两种算法的适用统一性，优势相长之处。

针对卡尔曼滤波算法对特殊日负残差偏大、无偏灰色模型多值预测上升趋势加快以及日负荷总趋势上升的情况，本文采用卡尔曼滤波与无偏灰色模型的最优线性组合模型进行短期日负荷预测。线性权重组合法在不改变原有算法的情况下，可以很好地规避由任一种方法预测误差偏大的情况，在本文算例以及文献[14-15]中均得到良好的预测结果。

线性权重组合法具体为

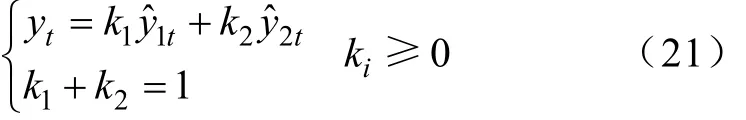
式中，1ˆty、2ˆty分别为卡尔曼滤波模型和无偏灰色理论模型的预测值；k1、k2为权重系数；yt为组合预测值。设有m个预测样本，ˆity为第i种预测模型第t个样本的拟合预测值，Yt为第t个样本的实际值，其预测的绝对误差为

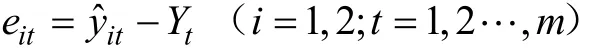
令et=yt−Yt，则有

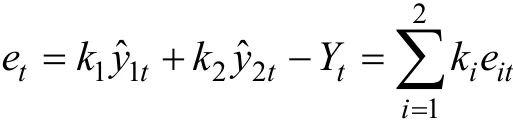
权重系数k1、k2，由平方和误差最小来求，其表达式为

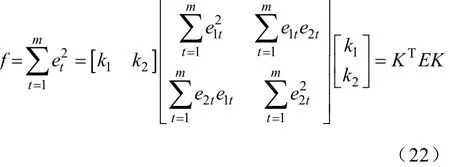
权重系数的求解用下列模型，即

式中，RT=[1,1],ki≥0(i=1,2)。对上式用拉格朗日乘子法求解，得

图1所示为卡尔曼滤波与无偏灰色组合法流程图。

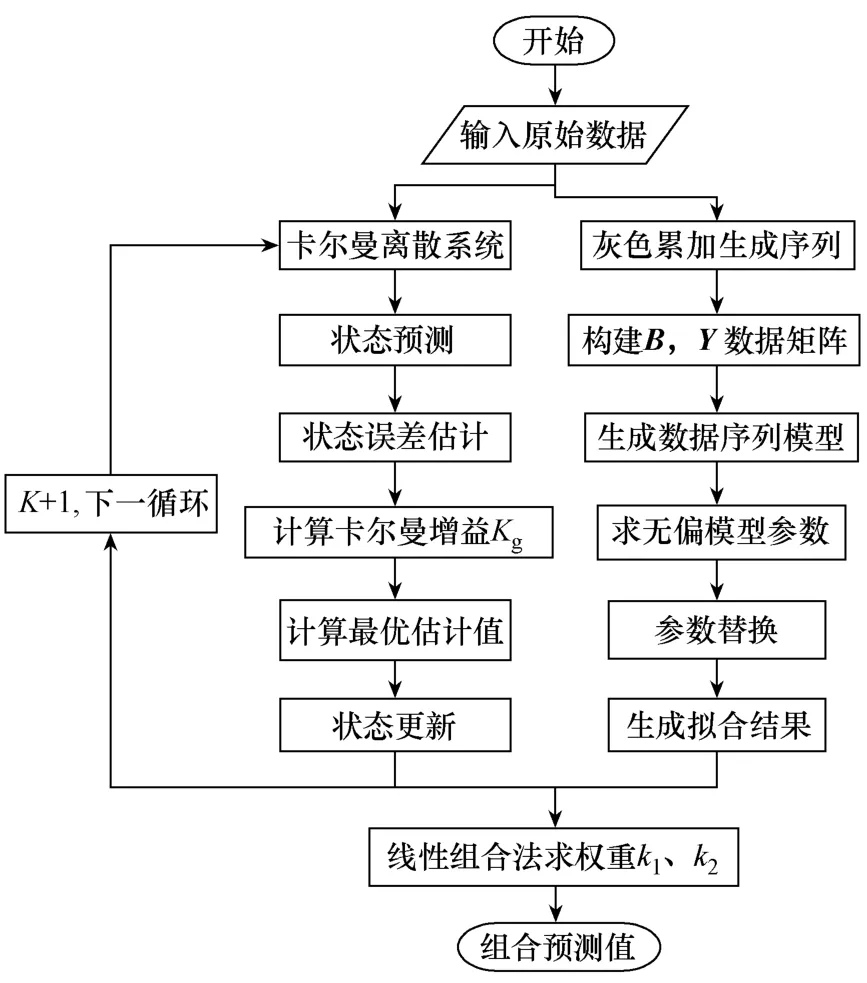
图1 卡尔曼滤波与无偏灰色组合模型流程图

4 算例与分析

本文以某地区连续6日同一时刻的负荷为例，分别采用卡尔曼滤波模型、无偏灰色模型、组合模型进行负荷预测。图2所示为单一模型与实际值的对比图。图3所示为卡尔曼滤波与无偏灰色组合法与实际值的对比图。表1所示为卡尔曼滤波模型、无偏灰色模型、组合法连续6日的预测值及相对误差。

图2中，卡尔曼滤波预测值与实际值在前3日误差较小且均为上升趋势，预测精度较高，但在第四日产生一个较前一日预测值下降且与实际值误差变大的预测值，这是由于卡尔曼滤波以最小均方误差估计的结果，它受前几日较小负荷值的影响，去除噪声的同时，无法准确估计负荷趋势与规律。而无偏灰色模型消除了灰色模型的固有偏差且建立潜在规律数列，预测数值较为平稳，趋势稳定，但是可能会因为起始实际值变小的情况而产生较大误差。

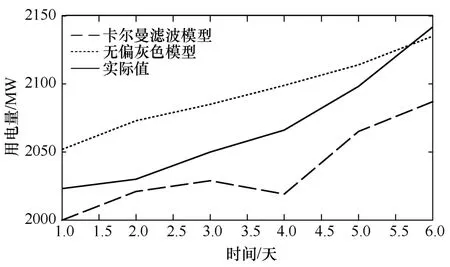
图2 单一模型预测值与实际值的比较

图3为卡尔曼滤波与无偏灰色组合法预测值与实际值对比。这两种算法的互补修正，组合预测法平均预测精度较高，且组合法任一日的预测误差均低于对应日两种单一模型中的最大预测误差，规避了两种算法中任意一种误差较大的情况，总体趋势不断趋近实际负荷预测值，取得了不错的预测效果。

图3 卡尔曼滤波与无偏灰色组合模型预测值与实际值比较

表1组合模型中卡尔曼滤波模型的权重系数占比为0.2528，无偏灰色模型权重系数占比较高，为0.7472，这是无偏灰色模型在本次预测数据中总体精度较高的体现。从表中可以发现，组合模型的相对误差总是小于卡尔曼滤波模型与无偏灰色模型的最大相对误差。例如4月6日，无偏灰色模型的相对误差较大为2.12%，而组合模型的相对误差仅1.48%；4月10日卡尔曼滤波模型的相对误差偏大为2.57%，而组合法相对误差只有0.89%。在4月5日、8日和9日组合法相对误差明显小于两种单一模型的相对误差，这是线性组合法的规避单一模型误差偏大的优点体现。两种单一模型在短期负荷预测中具有互补性。例如在4月6日负荷变化稳定属于正常日，卡尔曼滤波模型预测误差小为0.44%，而无偏灰色模型由于模型预测趋势上升的特性，预测误差较大为2.12%，进行组合后，组合模型的预测误差仅1.48%。在4月10日负荷变化较前几日陡增，属于特殊日。该日无偏灰色模型预测误差小为0.33%，卡尔曼滤波模型由于其预测是基于平均意义的最优估计，预测误差偏大为2.57%，进行组合预测后，预测误差仅为0.89%。

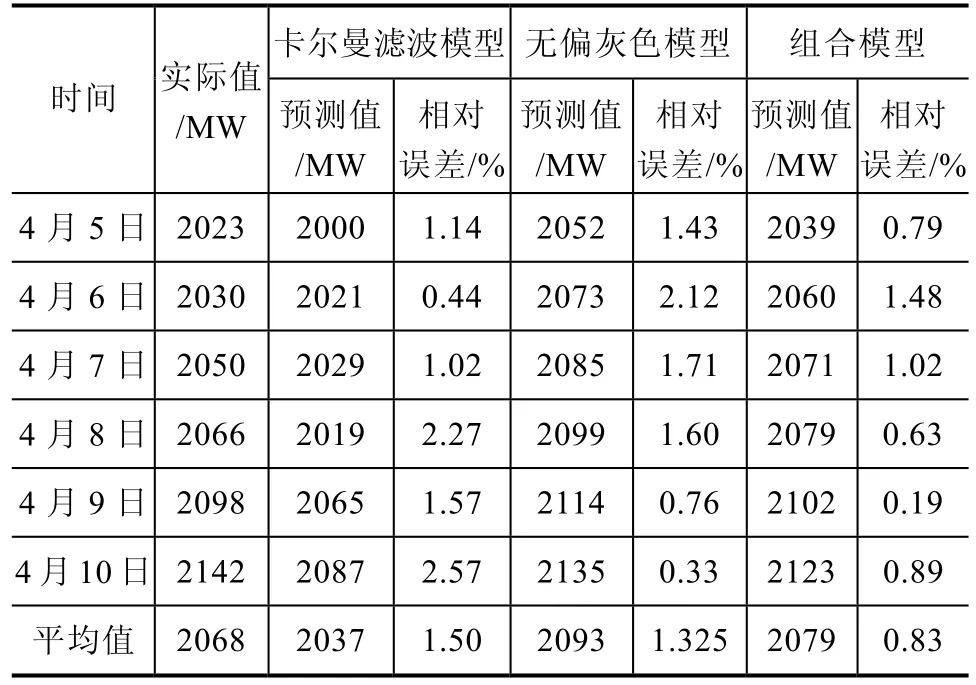
表1 三种预测模型的预测值及相对误差

5 结论

卡尔曼滤波模型能良好地估测动态系统，无偏灰色模型能在随机分布中挖掘潜在规律，而短期负荷恰好符合动态、随机的特点。本文运用最优权重组合法有效地结合卡尔曼滤波模型与无偏灰色模型，卡尔曼滤波模型过滤数据噪声，采用最小均方差估计，不断修正，得到基于平均意义的预测值，由无偏灰色模型弥补其特殊日收敛性不足的缺陷；利用最优权重组合法平衡了两种模型的最大误差，规避了误差过大的情况，并通过算例证明了该组合模型的在短期负荷预测中的可行性。

[1] Rahman S, Bhatnagar R. An expert system based algorithm for short-term load forecast[J]. IEEE Transactions on Power Systems, 1988, 3(2): 392-399.

[2] Ho K L, Hsu Y Y, Chen C F, et al. Short term load forecasting of Taiwan power system using a Know-ledgebased expert system[J]. IEEE Trans on Power Systems, 1990, 5(4): 1214-1221.

[3] 陈亚, 李萍. 基于神经网络的短期电力负荷预测仿真研究[J]. 电气技术, 2017, 18(1): 26-29.

[4] Haykin S. Neural networks: AComprehensive foundation[M]. NewYork: Macmillan College Publishing Company, 1994.

[5] Mastorocostas P A, Theocharis J B, Bakirtzis A G. Fuzzy modeling for short term load forecasting using the orthogonal least squares method[J]. IEEE Trans on Power Systems, 1999, 14(1): 29-36.

[6] Song K B, Baek Y S, Hong D H, et al. Short-term load forecasting for the holidays using fuzzy linear regression method[J]. IEEE Transactions on Power Systems, 2005, 20(1): 96-101.

[7] 于龙, 郑益慧, 王昕, 等. 基于SVM与相似日的短期电力负荷预测[J]. 电工技术学报, 2013, 28(1): 217-223.

[8] 水乃翔, 秦禹春. 关于灰色系统GM(1,1)模型的一些理论问题[J]. 系统工程理论与实践, 1998(4): 59-63.

[9] 穆勇. 无偏灰色GM(1,1)模型的直接建模法[J]. 系统工程与电子技术, 2003(9): 53-54.

[10] Ngan H W, Fung Y F, et al. An Advanced Evolutionary Algorithm for Load Forecasting with the Kalman Filter[A]. IEEE Conference Publication. HongKong: 2001. 134-138.

[11] 李明干, 孙健利, 刘沛. 基于卡尔曼滤波的电力系统短期负荷预测[J]. 继电器, 2004, 32(4): 9-12.

[12] Al-Hamadi H M. Soliman S A.short-term electric load forecastingbased on kalman filtering algorithm with moving Windows weatherand load model[J]. Electric Power Systems Research, 2004(68): 47-59.

[13] 邓自立. 卡尔曼滤波与维纳滤波-现代时间序列分析方法(Kalman Filter and Wiener Filter-Modern Time Serials Analysis)[M]. 哈尔滨: 哈尔滨工业大学出版社, 2001.

[14] 李林川, 吕冬, 武文杰. 一种简化的电力系统负荷线性组合预测法[J]. 电网技术, 2002, 26(10): 10-13.

[15] 张亚军, 刘志刚, 张大波. 一种基于多神经网络的组合负荷预测模型[J]. 电网技术, 2006, 30(21): 21-25.

Short Term Load Forecasting based on Kalman Filter and Unbiased Grey Combination Model

Lin Tianxiang1Zhang Ning1Hu Jun2
(1. School of Electrical Engineering and Automation, Fuzhou University, Fuzhou 350116; 2. Shanxi Zhangze Electric Power Co., Ltd, Taiyuan 030006)

According to the dynamic and stochastic characteristics of short-term load forecasting, a Kalman filtering and unbiased grey combination forecasting model is proposed. The model gives full play to the advantage of the Kalman filter to estimate the dynamic system, and makes use of the unbiased grey model to explore the characteristics of the random data. According to the defects of the special day convergence in the Kalman filter prediction, this paper makes use of the unbiased grey theory which is stable, regular and eliminates the inherent deviation. According to the trend that the trend of the unbiased grey theory is stable and the error of some data points in the short-term load forecasting is large, the Kalman filter is used to compensate the defect. Linear combination method is used to further avoid the prediction risk. The results show that the model has high precision and practicability.

Kalman filtering model; unbiased grey model; short term load forecasting; combination forecasting

林天祥（1996-），男，浙江省台州市人，本科，主要从事电力系统规划方面的研究工作。