基于最大电压偏差裕度的MMC子模块均压优化算法研究

曾 欢 李锐华 胡 波 胡 浩

（同济大学电气工程系，上海 201804）

基于最大电压偏差裕度的MMC子模块均压优化算法研究

曾 欢 李锐华 胡 波 胡 浩

（同济大学电气工程系，上海 201804）

根据模块化多电平换流器（MMC）的运行原理，针对传统子模块电容电压排序算法存在器件开关频率高、从而引起开关损耗较大的问题，本文提出一种基于最大电压偏差裕度的均压优化算法。该算法考虑了子模块上一时刻开关投切状态以及各子模块电压之间的差值，可以在保证各子模块电容电压基本一致的前提下，避免IGBT不必要的反复投切，有效降低MMC子模块开关频率，减小开关损耗，从而提高系统运行效率。本文通过在Matlab/Simulink平台上搭建21电平的MMC仿真模型进行了仿真，仿真结果验证了均压优化算法的正确性和有效性。

模块化多电平换流器；排序均压算法；开关频率；最大电压偏差裕度

MMC是一种新型的多电平电压源型变换电路，自2003年由Marquardt和Lesnicar提出以后就备受关注[1-3]。其通过将多个功率模块单元串联，可以叠加输出很高的电压，并具有输出谐波少、可四象限运行、模块化程度高、器件承受电压变化率低等优点[4-5]，因而在高压大功率的场合中得到广泛的应用。

由于MMC每个换流器桥臂含有很多个子模块、子模块悬浮电容的电压均衡问题直接影响着MMC的控制性能，因此，MMC子模块的电容均压问题一直得到广泛的关注和研究。现有电压均衡控制策略主要分为两种类型[6]：①基于电容电压大小进行排序的电压均衡算法，该类策略的原理和实现简单，因而得到普遍采用；②使用独立的子模块控制系统来稳定控制电容电压，而这些控制器的结构相对复杂，并且每个子模块都需要一个控制器，在实际应用中实现起来较为复杂，因此其应用受到一定的限制。

传统的电容电压排序算法需要先对采集到的电容电压实测后再进行排序，但当桥臂上各子模块电压之间的差值并不大的时候，将会导致同一子模块反复投切的情况，造成开关损耗较高，系统的运行效率降低[7]。为此许多文献在传统排序算法的基础上研究了其优化方法。文献[8]在排序前引入保持因子，使子模块在一定范围内可保持原来的开关状态，从而使器件的动作频率降低，但未针对保持因子的选取方法制定原则。文献[9]提出双保持因子，并通过闭环控制来稳定开关器件频率，但增大了控制系统的复杂度。文献[10-11]根据当前桥臂电流来计算子模块在下一控制周期中的电压变化，将预测值进行排序选择最适合投入的子模块，能有效降低开关频率，但计算过程复杂且对控制器的计算能力要求比较高。文献[12-14]考虑了各子模块间的电压差值，可提高子模块间的一致性，有效避免子模块间产生过大的电压偏差。文献[15]在桥臂子模块数改变时，投入或切出电压最高或最低的子模块，可以使开关频率接近基频，但会造成子模块电容电压的过大波动。

综上所述，若子模块电容电压的均衡度与开关频率存在矛盾，电容电压允许偏差越大，则开关频率越低；若电容电压允许偏差越小，则开关频率越高。本文在分析了MMC的拓扑结构和运行原理的基础上，针对现有排序算法的不足进行改进，提出新的优化均压算法，在降低器件开关动作频率的同时，也能避免过大的电压偏差。

1 MMC拓扑结构与子模块投切原理

图1为三相MMC主电路拓扑及子模块结构示意图，换流器由三相六桥臂组成，其中每相由上下两个桥臂构成，N个子模块串联1个桥臂等效电感L组成单个桥臂。

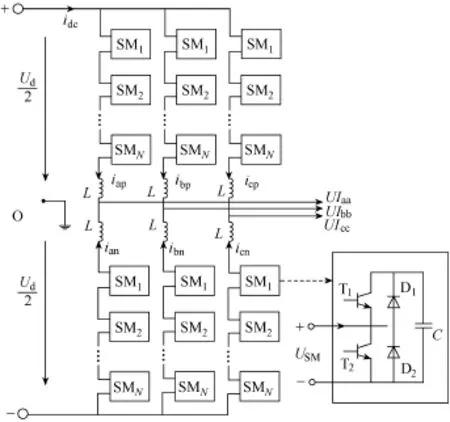
图1 MMC主电路拓扑示意图

如图1所示，半桥子模块由2个IGBT（T1和 T2）、2个反并联二极管（D1和D2）和1个直流电容C组成。图中dU为直流侧电压，dcI为直流侧电流，aU、bU和cU为交流侧三相电压，aI、bI和cI为交流侧三相电流，api、bpi和cpi为ABC三相上桥臂电流，ani、bni和cni为ABC三相下桥臂电流，SMU为子模块输出电压，“O”点为直流侧的虚拟中性点。

MMC的脉冲调制技术直接影响到系统的工作效率和开关器件的实际工作频率，因此国内外学者对其进行了广泛地研究。常见的调制方式有最近电平逼近调制和载波移相PWM调制[16]。其中，最近电平逼近调制实现方法较简单，器件的开关频率较低，适用于桥臂子模块数量较大（即输出电平数较多，一般在19电平以上）的应用场合。因此，本文采用适用于模块数较多情况下的最近电平逼近调制。

为了说明MMC的子模块投切原理，以A相为例，记A相上桥臂电压为apU，下桥臂电压为anU，A相输出电压为aU，则由基尔霍夫电压定律可得

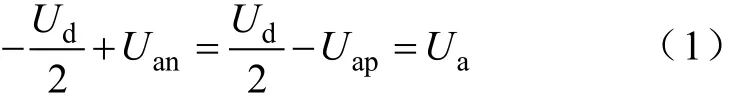
同时，MMC上下桥臂投入的子模块总数需保持不变：

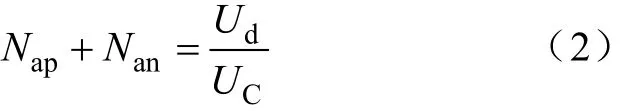
式中，apN为A相上桥臂投入的子模块数；anN为下桥臂投入的子模块数，CU为子模块电容电压。联立式（1）和式（2），可得

式中，round(x)表示取与x最接近的整数。

2 MMC电容电压排序优化算法

基于电压排序的选择机制控制策略是，将MMC调制策略所得到的开关脉冲信号，合理分配给桥臂上的每个子模块，在满足输出电压不变的前提下，重新选择需要投入和切除的子模块，从而避免该桥臂上各子模块电容电压形成过大的偏差。

2.1 传统排序算法

MMC传统的电压排序均压算法如图2所示。首先通过MMC调制策略，获得此时该桥臂需要投入的子模块数onn，然后检测此时该桥臂的电流方向。若此时桥臂电流方向为正，投入状态的子模块可以吸收有功功率，以提升电容电压，则将此时该桥臂内电压最低的onn个子模块投入工作。反之，若此时桥臂电流方向为负，投入状态的子模块可以释放有功功率，则此时该桥臂内电压最高的onn个子模块投入工作。

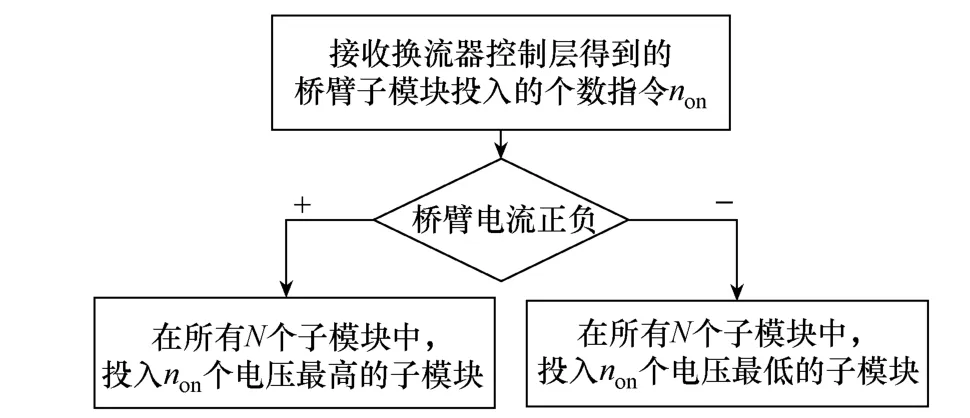
图2 传统电压排序均压算法

该方法由于未设定调整开关脉冲的触发前提，使得在每个触发周期中都使用了该算法对投切状态进行重新选择。桥臂上各子模块间的电压只有很小的偏差，或者桥臂上需要投入使用的子模块总数并没有发生变化，一旦经排序后的结果发生改变，就需要调整所有子模块的开关状态。这会导致同一IGBT不必要的反复投切，提高了器件的开关频率，从而增加了MMC的开关损耗。

2.2 电容电压排序优化算法

为了降低器件的开关频率，现有的均压优化算法有基于投入子模块数变化量的优化均压算法，其控制原理如图3所示。该算法当投入的桥臂子模块数改变时，投入或切出电压最高或最低的子模块，可以降低器件的平均开关频率，由于未限制各子模块间的电压偏差，各子模块电容电压仍然存在不一致的情况，从而引起上下桥臂之间环流增大的问题。

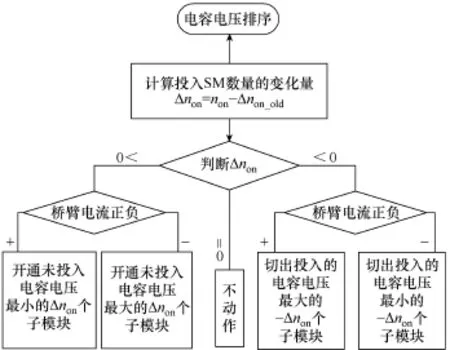
图3 基于投入子模块数变化量的优化均压算法

针对上述问题，本文在现有优化算法的基础上提出改进型电压排序均压策略，通过分析桥臂子模块上一触发周期的投切状态以及各子模块电容电压之间的差值，生成新的触发脉冲序列，以降低子模块的开关频率，其原理如图4所示。

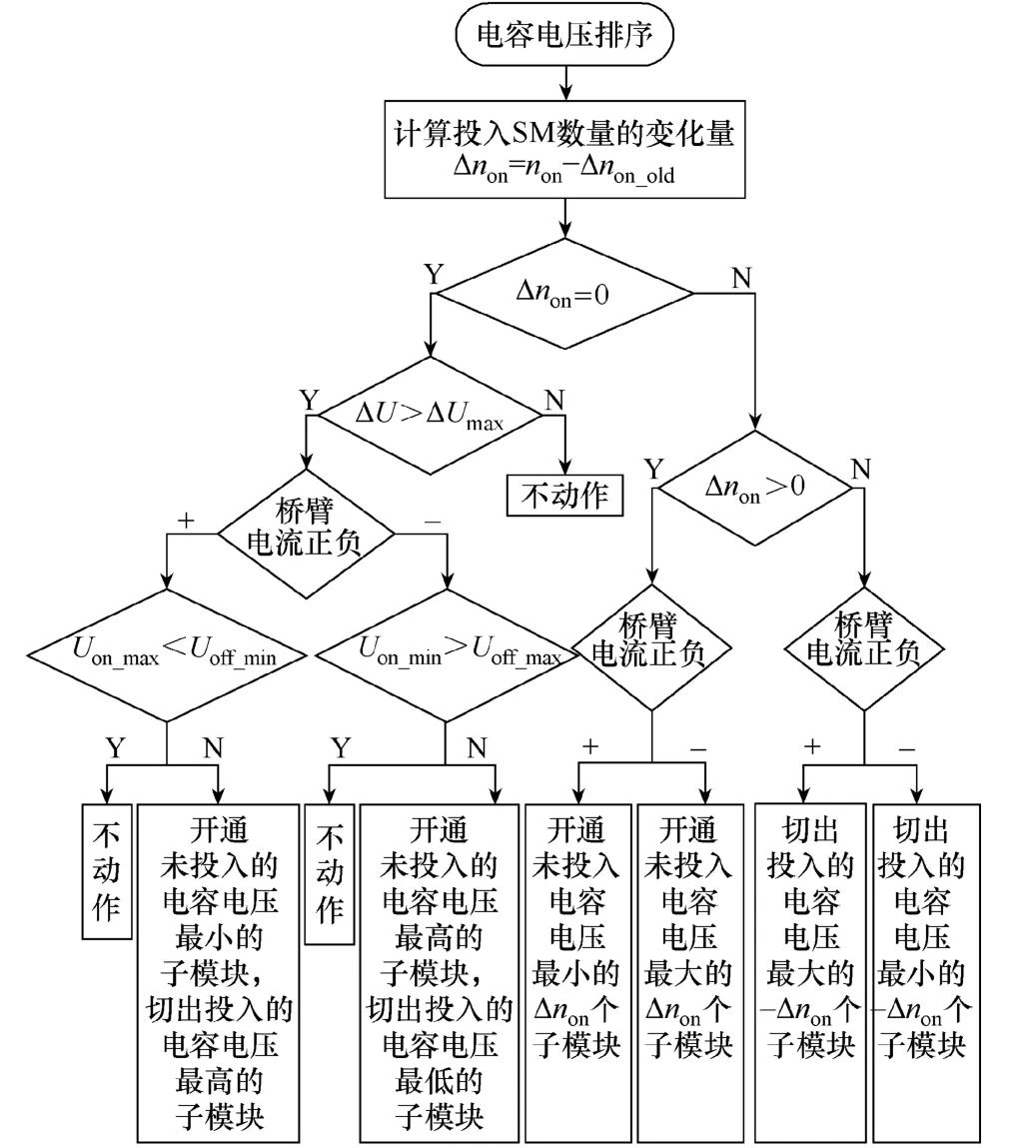
图4 改进型电压排序均压算法

改进型电压排序均压算法，先经过MMC调制策略，得到下一周期该桥臂需要开通的子模块数non，并与上一触发周期该桥臂已投入的子模块数non_old相减，可得投入子模块数的变化量为

当Δnon＞0时，即该桥臂需要投入更多的子模块，此时需要判断该桥臂电流的方向。若桥臂电流方向为正，即投入后的子模块电容电压将升高，则将上一触发周期处于切除状态的N−non_old个子模块中，开通电容电压最低的Δnon个子模块；类似的，若桥臂电流方向为负，即投入状态的子模块电容电压将下降，则将上一触发周期该桥臂内处于切除状态的N−non_old个子模块中，将电压最高的Δnon个子模块开通。反之，当Δnon＜0时，先判断该桥臂电流的方向，若桥臂电流方向为正，则将上一触发周期处于投入状态的non_old个子模块中，电压最高的Δnon个子模块予以切除；若桥臂电流方向为负，则将上一触发周期该桥臂内处于投入状态的non_old个子模块中，电压最低的个子模块予以切除。

当Δnon=0时，为了将子模块电容电压之间的差值控制在一定范围内，定义Umax为该桥臂所有子模块瞬时电容电压中的最大值，Umin为该桥臂所有子模块瞬时电容电压中的最小值，ΔU为Umax和Umin的差值，ΔUmax为提前设定的最大电压偏差裕度。

当ΔU≤ΔUmax，即此时子模块电容电压偏差在允许的范围之内时，保持现有触发脉冲。当ΔU＞ΔUmax时，先判断该桥臂电流的方向。若桥臂电流方向为正，当投入的子模块中电压最大值小于未投入的子模块中电压最小值时，则保持现有触发脉冲；否则，将未投入的电容电压最小的子模块投入，将已投入的电容电压最高的子模块切除。类似，若桥臂电流方向为负，当投入的子模块中电压最小值大于未投入的子模块中电压最大值时，则保持现有触发脉冲；否则，将未投入的电容电压最高的子模块投入工作，将已经投入的电容电压最低的子模块切除。

本文提出的优化排序算法可以将桥臂电流所承载的电荷快速并且均匀地分配到各子模块电容上，从而有效降低子模块的平均开关频率，同时还能限制子模块电容电压之间的偏差，使各个子模块间的电容电压基本保持一致。

3 仿真验证与分析

为验证本文所提出的优化排序算法的正确性和有效性，在Matlab/Simulink中搭建了21电平的MMC仿真模型，并对逆变工况进行了仿真。系统的基本参数见表1。

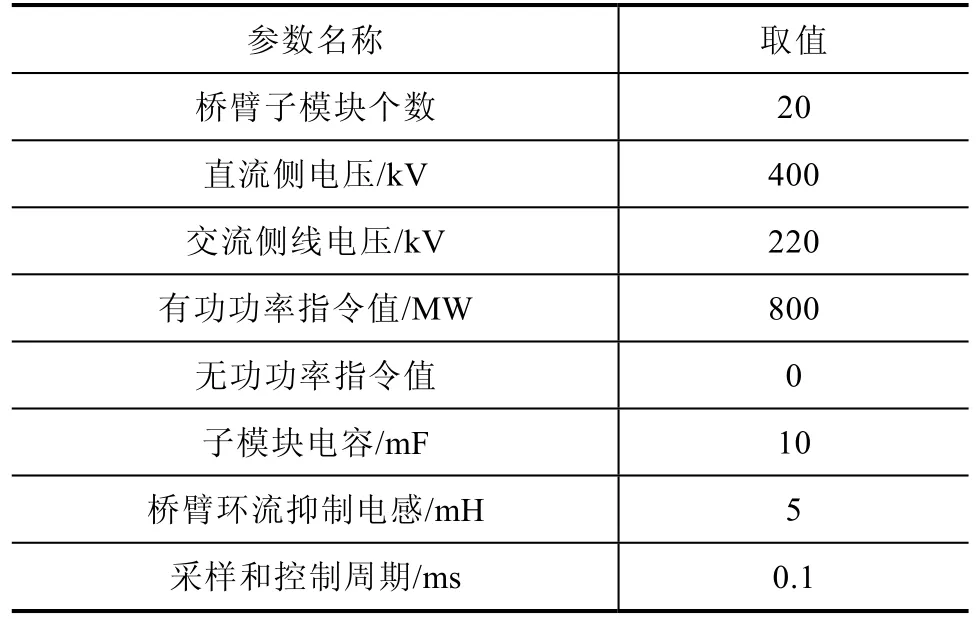
表1 MMC仿真模型参数

首先，对使用传统排序算法的模型进行了仿真，仿真结果以A相上桥臂（串联子模块数为20）为例，图5是A相上桥臂各子模块电容电压波形，可以看出子模块电容电压保持稳定，电压波动幅度小于3%，并且各子模块之间具有非常高的一致性。进一步分析可得，A相器件的平均开关频率为2460Hz，桥臂电流（以A相上桥臂为例）谐波畸变率THD为48.03%，交流侧电压THD为3.10%，交流侧电流THD为2.01%。

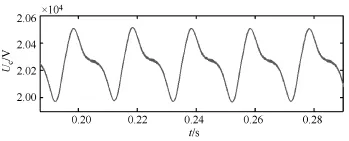
图5 传统算法下的A相各子模块电容电压

接着，对基于投入子模块数变化量的优化均压算法进行了仿真，图6是A相上桥臂各子模块电容电压波形，可以看出各子模块电容电压之间存在较大的偏差。进一步分析可得，A相器件的平均开关频率为396Hz，桥臂电流THD为55.87%，交流侧电压THD为3.13%，交流侧电流THD为2.01%。

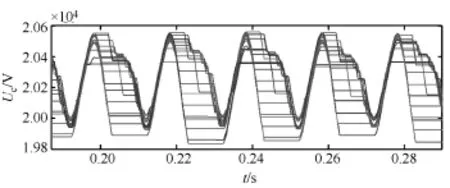
图6 基于投入子模块数变化量的优化算法下的A相各子模块电容电压

最后，对本文提出的基于最大电压偏差裕度的改进型优化均压算法进行了仿真分析，其中最大电压偏差裕度maxUΔ分别设为800V、500V、200V、100V和50V。以A相上桥臂（串联子模块数为20）为例，各子模块电容电压经优化后的电压波形如图7所示，可以看出子模块电容电压可保持稳定，并且随着最大电压偏差裕度maxUΔ设定值的减小，子模块电容电压之间的偏差不断减小。

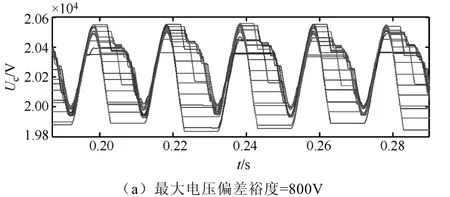
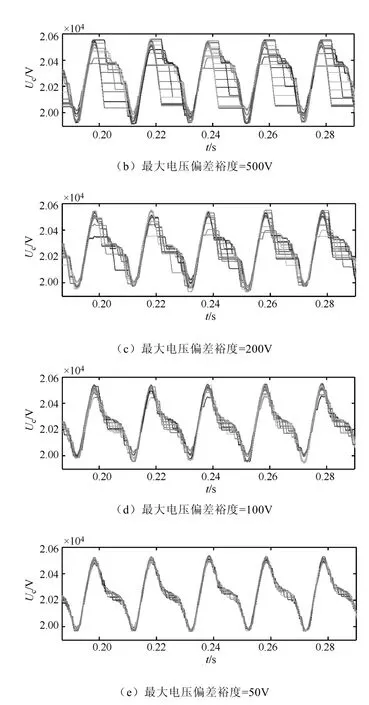
图7 改进型优化算法下的A相各子模块电容电压

通过对传统排序算法和两种优化算法下的平均开关频率、桥臂电流THD、交流侧电压THD和交流侧电流THD四项指标进行分析和比较，统计结果见表2。

从表2中分析可得，与传统算法相比，本文所提出的优化算法可以很大程度上减小器件的平均开关频率，以最大电压偏差裕度为200为例，平均开关频率从2460Hz降低到527Hz，减小了74%。最大电压偏差裕度设置得越大，器件的平均开关频率下降也就越多，器件频繁开通的可能性也就越低，从而开关损耗降低得越多，有利于提高系统运行效率。同时，交流侧电压电流的THD和桥臂电流的THD与传统排序算法下的结果相比几乎不变，这表明优化后的策略不会影响到MMC的正常运行。

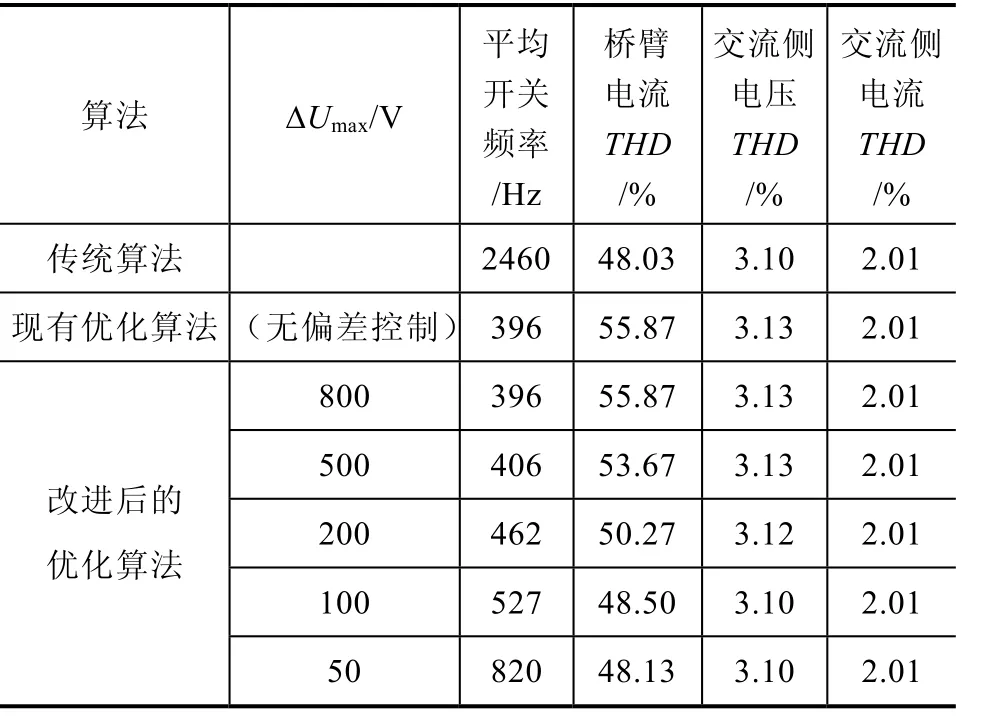
表2 不同算法的仿真结果

另外，从图6、图7和表2中可以看出，与现有均压优化算法相比，本文所提出的改进型电容均压优化算法能够更好地保证各子模块电容电压的一致性。另一方面，与传统算法相比，现有的优化算法虽然可以降低开关频率，但同时增加了桥臂的环流。而本文所提出的算法，在不增加系统环流的情况下，有效降低了开关频率，减少了子模块的投切次数，因而从整体上提升了MMC的运行性能。

4 结论

本文针对传统子模块电容电压排序算法会导致器件开关频率增大的问题，提出一种新的电容电压排序优化算法。该算法通过分析子模块上一时刻的投切状态使其具有保持原来投切状态的能力，并且通过引入最大电压偏差裕度来限制各子模块电容电压的偏差。仿真结果表明，本文提出的排序均压优化算法在不增加系统环流的情况下能后降低开关频率，减小子模块投切次数，从整体上提高MMC运行性能，为MMC的子模块均压控制策略提供了一种新的方法。

[1] Lesnicar A, Marquardt R. An innovative modular multilevel converter topology suitable for a wide power range[C]//Power Tech Conference Proceedings, 2003 IEEE Bologna. IEEE, 2003(3): 6.

[2] 康伟, 龙云波, 宗波, 等. 集成化的模块化多电平换流器功率模块设计与研制[J]. 电气技术, 2015, 16(2):17-22.

[3] 佚名. 基于双电容模块的MMC型多端口电力电子变压器[J]. 电气技术, 2016, 17(8): 81-81.

[4] 杨晓峰, 林智钦, 郑琼林, 等. 模块组合多电平变换器的研究综述[J]. 中国电机工程学报, 2013, 33(6): 1-14, 前插1.

[5] 张建坡, 赵成勇, 孙海峰, 等. 模块化多电平换流器改进拓扑结构及其应用[J]. 电工技术学报, 2014, 29(8): 173-179.

[6] 黄守道, 廖武, 高剑, 等. 基于改进均压算法的模块化多电平变流器开关频率分析[J]. 电工技术学报, 2016, 31(13): 36-45.

[7] Debnath S, Qin Jiangchao, Bahrani B, et al. Operation, control, and applications of the modular multilevel converter: a review[J]. IEEE Transactions on Power Electronics, 2015, 30(1, SI): 37-53.

[8] 管敏渊, 徐政. MMC型VSC-HVDC系统电容电压的优化平衡控制[J]. 中国电机工程学报, 2011, 31(12): 9-14.

[9] 郭裕群, 赵成勇, 许建中, 等. 模块化多电平换流器子模块平均开关频率的精确控制方法[J]. 电力系统自动化, 2016, 40(19): 94-100.

[10] 何志兴, 罗安, 熊桥坡, 等. 模块化多电平变换器模型预测控制[J]. 中国电机工程学报, 2016, 36(5): 1366-1375.

[11] Qin Jiangchao, Saeedifard M. Reduced switchingfrequency voltage-balancing strategies for modular multilevel HVDC converters[J]. IEEE Transactions on Power Delivery, 2013, 28(4): 2403-2410.

[12] 丁冠军, 丁明, 汤广福, 等. 新型多电平VSC子模块电容参数与均压策略[J]. 中国电机工程学报, 2009(30): 1-6.

[13] Jia X, Liu J, Zhang J. The research of capacitor voltage balancing strategy of MMC[C]//International Conference on Civil, Materials and Environmental Sciences, 2015.

[14] 郭高朋, 姚良忠, 温家良. 模块化多电平变流器的子模块分组调制及均压控制[J]. 中国电机工程学报, 2016, 36(1): 145-153.

[15] Tu Qingrui, Zheng Xu, Xu Lie. Reduced Switching-Frequency modulation and circulating current suppression for modular multilevel converters[J]. Power Delivery, IEEE Transactions on, 2011, 26(3): 2009-2017.

[16] Chai R Z, Zhang B H, Hao Z G, et al. A low switching frequency voltage balancing strategy of modular multilevel converter[C]//on 2013-2013, 2013: 1-4.

The Research of Optimized Capacitor Voltage Balancing Algorithm of MMC based on Maximum Voltage Deviation Margin

Zeng Huan Li Ruihua Hu Bo Hu Hao
(Electrical Engineering of Tongji University, Shanghai 201804)

The traditional capacitor voltage balancing arithmetic results in high switching frequency and high switching losses. In order to solve this problem, this paper studies the operating principle of modular multilevel converter (MMC) and proposes an optimized capacitor voltage balancing algorithm based on maximum voltage deviation margin. This is done by considering the switching status and voltage deviation of submodules, which can reduce the switching frequency of IGBT under satisfying the balance demand, thus reducing switching losses and improving the efficiency of the system. At last, the simulation based on a 21-level three-phase MMC in Matlab/Simulink verifies the validity and effectiveness of the proposed algorithm.

MMC; capacitor voltage balancing arithmetic; switching frequency; voltage deviation

曾 欢（1994-），男，江西吉安人，同济大学在读硕士研究生，主要研究方向为电力电子技术。