基于球面坐标的目标定位位置的封闭解算法*

田丽芳

(黄淮学院信息工程学院,河南 驻马店 463000)

基于球面坐标的目标定位位置的封闭解算法*

田丽芳*

(黄淮学院信息工程学院,河南 驻马店 463000)

针对无线传感网络WSNs(Wireless Sensor Networks)的三维目标定位问题,提出基于接收信号强度RSS(

Signal Strength)和到达角度AoA(Angle of Arrival)混合目标定位RATL(RSS and AoA-based Target Localization algorithm)算法。RATL算法融合了RSS和AoA观察值。通过将笛卡尔坐标转换球面坐标,并充分利用AoA测量值的优势,RATL算法建立测量值与未知目标位置间的关系,进而获取简单、封闭解。相比于现在算法,RATL算法并不要求更多松驰。实验数据表明,RATL算法比同类算法的复杂度低、定位精度高。

无线传感网络;目标定位;接收信号强度;到达角度

1 定位模型

令x∈R3表示目标未知位置。而N个已知锚节点表示为ai∈R3,i=1,…,N。通过结合RSS测距和角度测距算法估计目标位置,定位模型如图1所示。

假定目标位置的笛卡尔坐标为x=[xx,xy,xz]T,而第i个锚节点的笛卡尔坐标为ai=[aix,aiy,aiz]T。图1中的di、φi和αi分别表示目标离第i个锚节点间距离、方位角和仰角。

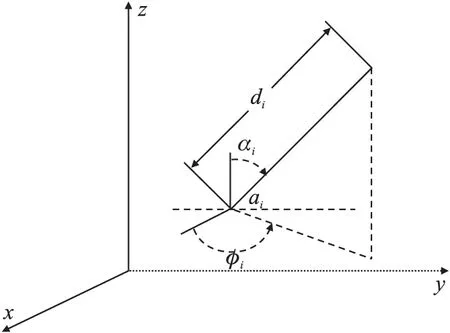
图1 定位模型

由于RSS测距无需额外硬件设备[17],利用RSS值进行测距。假定目标与i个锚节点间的RSS值Pi,定义如式(1)所示[18]:

(1)

通过全向天线或天线阵列可获取AoA测量。因此,利用简单的几何理论,可得到方位角和仰角[8]测量值:

(2)

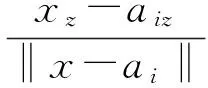
(3)

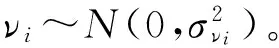
假定观察矢量θ=[PT,φT,αT],且θ∈R3N,其中P=[Pi]、φ=[φi]和α=[αi]。

假定高斯白噪声的概率密度函数如式(4)所示:

(4)

式中:σi=[σni,σmi,σνi]T。

而函数f(x):f(x)=

(5)

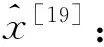
(6)

2 RATL定位算法

RATL定位算法框图如图2所示。首先,通过将笛卡尔坐标转换成球面坐标,降低算法复杂度,然后分别在已知发射功率和未知发射功率两种情况下进行位置估计。同时,分别利用最大似然估计算法,计算距离权值和基于功率权值。利用这些权值分别优化已知发射功率和未知发射功率条件下的WLS位置估计算法,最终获取目标位置的闭合解。

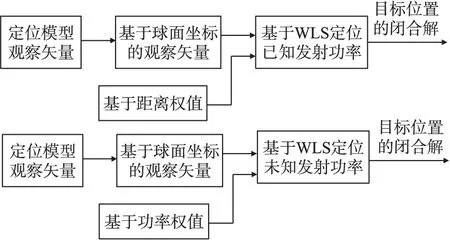
图2 RATL定位算法模型

2.1 球面坐标

首先,对式(6)进行转换成轻量表述。同时将笛卡尔坐标转换成球面坐标,进而获取有效解,这也有利于表述角度测量值。因此,式(1)～式(3)可分别重写为:

λi‖x-αi‖≈ηd0i=1,…,N

(7)

(8)

kT(x-ai)≈‖x-α‖cos(ai)i=1,…,N

(9)

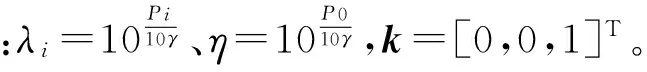
通过转换球面坐标,可将x-αi表述为:

x-αi=riui:ri≥0,i=1,…,N

(10)

式中:‖ui‖=1为单位矢量。

利用AoA信息表述单位矢量ui,可得:ui=[cos(φi)sin(αi),sin(φi)sin(αi),cos(αi)]

(11)

利用式(10)和式(11)代入式(7)和式(9),可得:

(12)

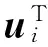
(13)

接下来,从两种情况讨论估计目标节点位置。这两种情况分别是:已知发射功率PT和未知发射功率PT。

2.2 已知发射功率PT

为了获取更准确表述链路差异,RATL算法引用了权值。目标与第i个锚节点的权值Wi可表述为:

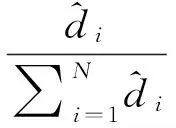
(14)

从式(14)可知,距离越短,权值越大。原因在于:离目标越近,RSS和AoA测量值的误差小的概率越大。RSS测量值与距离有多个乘性因子[17],这导致偏远链路与邻近链路的误差更大。为此,使用权值的AoA测量值进行调整,如图3所示。

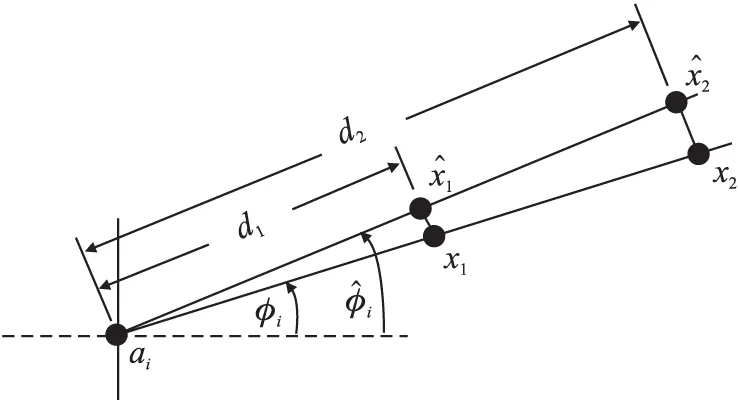
图3 基于权值的AoA测量值

依据权重最小二乘法,并结合式(8)、式(12)～式(14),可得目标位置的估计值:

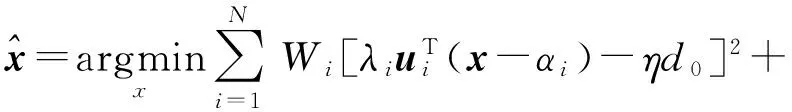
(15)

将式(15)写成一般的矢量形式,如式(16)所示:

(16)

式中:W=I3⊗diag(W),其中⊗表示克罗内克积。且矢量A可表示为:

(17)

而矢量b的定义如式(18)所示:

(18)

因此,式(16)的闭合解可表述为:

(19)

2.3 未知发射功率

在实际环境中,可能难以获取发射功率PT,即多数情况PT是未知的。因此,本小节讨论在未知发射功率环境下,如何估计目标位置。

(20)

依据WLS原理,可得:

(21)

式(21)也可表述为:

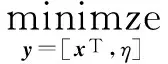
(22)

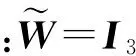
(23)

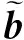
(24)

因此,式(21)的闭合解可表述为:

(25)

3 性能分析

3.1 算法复杂性

复杂性是算法性能的一项重要指标。为此,选择文献[9]的最小二乘LS算法(已知发射功率)、文献[14]的已知发射功率的SOCP算法、文献[15]的已知发射功率的SR-WLS算法和文献[16]的已知发射功率的WLLS算法作为参照。选用SR-WLS算法作为参照,原因在于SR-WLS算法也是引用RSS和AoA的混合定位算法,与RATL算法具有比较性。

它们的算法复杂性如表1所示,其中N表示锚节点数。而RATL-K、RATL-UK分别表示已知发射功率、未知发射功率下的目标定位算法。

表1 算法复杂性

从表1可知提出的RATL算法复杂性并不高于同类算法,且与N呈线性关系。

3.2 算法位置估计准确性

为了分析算法的性能,引用MATLAB建立仿真平台。实验参数如表2所示,其中路径衰落指数PLE不采用固定值,而是使其服从均匀分布,即γi～U[2.2,2.8],且i=1,…,N。此外,通信半径为250 m,节点总数为50。

本小节分析算法定位的准确性,选用定位均方误差RMSE作为性能指标,其定义如式(26)所示:

(26)

表2 仿真参数

首先分析锚节点数N对RMSE的影响。实验数据如图4所示,其中σni=6 dB、σmi=10和συi=10。从图4可知,各算法的RMSE随N的增加而下降。原因在于,锚节点数越多,越能获得更多测距信息,有利于测距准确性的提高。此外,与其他算法相比,提出的RATL算法降低了RMSE,提高了定位准确性。即使在未知发射功率的情况下,RATL算法的RMSE仍低于同类算法,这说明利用AOA和RSS的混合算法,在不增加算法复杂度同时,提高了算法的定位精度。

图4 RMSE随N的变化曲线

图5 RMSE随测距噪声σni的变化曲线(N=4)

然后,再分别分析测距噪声σni、方位角测量误差σmi和仰角测量误差σνi对RMSE的性能影响,N=4。实验数据分别如图5～图7所示。

观察图5～图7可知,不同的测量误差对RMSE性能影响存在差异。不难发现,所有算法随着测距误差的增加,算法的RMSE性能下降。然而,它们的下降速度并不相同。例如,RSS测距误差对RATL算法的RMSE影响较小。而AoA测量值对RMSE有较大的影响,原因在于:RATL算法更依赖于角度测量值,而不是测距测量值。此外,与同类算法相比,提出的RATL算法的RMSE得到有效地下降,这充分说明RATL算法能有效地降低定位误差。

图6 RMSE随方位角测量误差σmi的变化曲线(N=4)

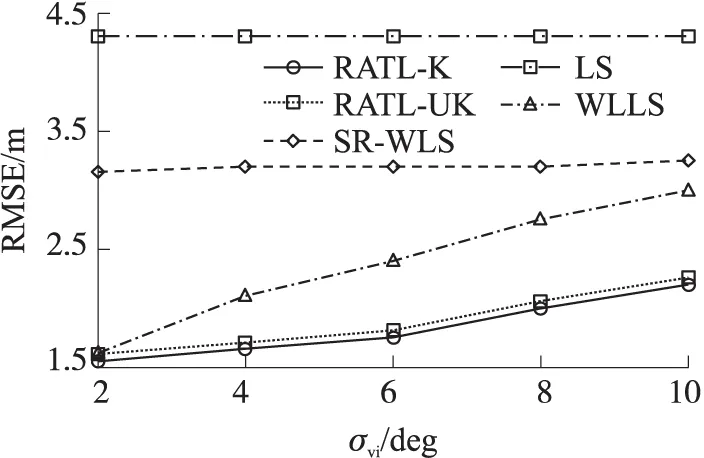
图7 RMSE随仰角测量误差σνi的变化曲线(N=4)

4 总结

针对3-D的目标定位问题,提出基于RSS和AoA的混合定位算法RATL。RATL算法通过转换坐标,并结合AoA测距优势,建立测距值与目标位置间关系,再通过WLS算法获取目标位置的封闭解。实验数据表明,提出的RATL算法有效地提高了定位精度,降低了定位均方误差。

通过实验数据可知,RATL算法降低了RMSE。然而,由于RATL算法需要测量RSS和角度信息,只适合中小型WSNs应用场景。

[1] Bartoletti S,Dai W,Conti A,et al. A Mathematical Model for Wideband Ranging[J]. IEEE J Sel Topics Signal Process,2015,9(2):216-228.

[2] Tomic S,Beko M,Dinis R. RSS-Based Localization in Wireless Sensor Networks Using Convex Relaxation:Non-Cooperative and Cooperative Schemes[J]. IEEE Trans Veh Technol,2015,64(5):2037-2050.

[3] Tomic S,Beko M,Dinis R. Distributed RSS-AoA Based Localization with Unknown Transmit Powers[J]. IEEE Wireless Commun Lett,2016,5(4):392-395.

[4] 刘卉,李泽军. 基于投影矢量的双组播树高效路由数据收集[J]. 传感技术学报,2013,26(4):570-577.

[5] Dai W,Shen Y,Win M Z. Energy-Efficient Network Navigation Algorithms[J]. IEEE J Sel Areas Commun,2015,33(7):1418-1430.

[6] Dai W,Shen Y,Win M Z. Distributed Power Allocation for Cooperative Wireless Network Localization[J]. IEEE J Sel Areas Commun,2015,33(1):28-40.

[7] 李云飞,江明,娄柯. 无线传感器网络中DV-Hop定位算法的改进[J]. 计算机工程与应用,2014,50(3):79-83.

[8] 金纯,叶诚,韩志斌. 无线传感器网络中DV-Hop定位算法的改进[J]. 计算机工程与设计,2013,34(2):401-405.

[9] Yu K. 3-D Localization Error Analysis in Wireless Networks[J]. IEEE Trans Wireless Commun,2016,6(10):3472-3481.

[10] Wang S,Jackson B R,Inkol R. Hybrid RSS/AOA Emitter Location Estimation Based on Least Squares and Maximum Likelihood Criteria[C]//Proc IEEE QBSC,Kingston,ON,Canada,2012:24-29.

[11] Gazzah L,Najjar L,Besbes H. Selective Hybrid RSS/AOA Weighting Algorithm for NLOS Intra Cell Localization[C]//Proc IEEE WCNC,Istanbul,Turkey,Apr. 2014::2546-2551.

[12] Chan Y T,Chan F,Read W,et al. Hybrid localization of an Emitter by Combining Angle-of-Arrival and Received Signal Strength Measurements[C]//Proc IEEE CCECE,Toronto,ON,Canada,2014:1-5.

[13] Biswas P,Aghajan H,Ye Y. Semidefinite Programming Algorithms for Sensor Network Localization Using Angle Information[C]//Proc Annu Asilomar Conf Signals Syst Comput,Pacific Grove,CA,USA,2015:220-224.

[14] Tomic S,Marikj M,Beko M,et al. Hybrid RSS-AoA Technique for 3-D Node Localization in Wireless Sensor Networks[C]//Proc IWCMC,Dubrovnik,Croatia,Aug. 2015:1277-1282.

[15] Tomic S,Beko M,Dinis R. 3-D Target Localization in Wireless Sensor Network Using RSS and AoA Measurement[J]. IEEE Trans Veh Technol,2015,6(8):34-42.

[16] Khan M W,Salman N,Kemp A H,et al. Localization of Sensor Nodes with Hybrid Measurements in Wireless Sensor Network[J]. Sensors,2016,16(7):1-16.

[17] Patwari N,Ash J N,Kyperountas S,et al. Locating the Nodes:Cooperative Localization in Wireless Sensor Networks[J]. IEEE Signal Process Mag,2015,22(4):54-69.

[18] Rappaport T S. Wireless Communications:Principles and Practice. Upper Saddle River,NJ,USA:Prentice-Hall,1996.

[19] Kay S M. Fundamentals of Statistical Signal Processing:Estimation Theory. Englewood Cliffs,NJ,USA:Prentice-Hall,1993.

田丽芳(1981-),女,汉族,山西长治人,硕士,讲师,研究方向为软件测试,算法设计。

AClosed-FormforSphericalCoordinates-BasedTargetLocalizationAlgorithminWirelessSensorNetworks*

TIANLifang*

(School of Information Engineering,Huanghuai University,Zhumadian He’nan 463000,China)

This paper addresses the problem of target localization in a 3-D space in Wireless Sensor Networks(WSNs). We propose a novel target localization algorithm for 3-D space that merges RSS and AoA observations,which is marked as RATL. By shifting from Cartesian to spherical coordinates and taking advantage of the acquired AoA measurements,we build new relationships between the measurements and the unknown target location,which results in a simple and closed-form solution. In contrast to the existing methods,the proposed one does not require further relaxations(which enlarge the set of possible solutions). The new method is computationally light and our numerical results show that it provides excellent accuracy,surpassing the state-of-the-art methods in general.

wireless sensor networks;target localization;received signal strength;angle of arrival

Signal Strength)和到达角度AoA(Angle of Arrival)混合目标定位RATL(RSS and AoA-based Target Localization algorithm)算法。通过球面坐标转换建立测距值与目标位置的关系,然后推导了简单的闭合求解位置算法。实验数据表明,提出的RATL定位算法具有低的定位误差,并且在发射功率未知环境下估计目标位置。

项目来源:基于物联网的光伏温室大棚系统构建研究(2015GGJS-300)

2017-03-23修改日期:2017-05-23

TP393

:A

:1004-1699(2017)09-1433-05

10.3969/j.issn.1004-1699.2017.09.023

由于在军队和工程应用的重要性[1-6],目标定位已受到广泛关注。多数无线定位算法依赖于测距算法[3]。常见的测距算法有基于到达时间ToA(Time of Arrival)、接收信号强度RSS(Received Signal Strength)和到达角度AoA(Angle of Arrival)[7-8]。

目前,研究人员已提出了不同测距或角度的定位算法[9-16]。文献[9]提出了线性最小二乘LS(Least Squares)定位算法。而文献[10]提出基于LS和最大似然关系ML(Maximum Likelihood)估计的混合定位算法。而文献[11]提出了基于权重LS(Weighted LS,WLS)的RSS/AoA测距的混合定位算法。类似地,文献[12]也提出了基于WLS的RSS差/AoA混合定位算法。而文献[14]提出SOCP(Second Order Cone Programming)算法,通过SOCP降低算法复杂度,并提高定位精度。而文献[16]提出权重线性估计WLLS(Weighted Linear LS)算法。

这些算法具有一定的代表性,但是,这些算法均存在不足。文献[10-13]提出的算法仅是基于2-D场景,而文献[12]只适用于低噪声功率环境。文献[13-15]提出的定位算法引用了复杂数学表述,这极大地增加了算法的复杂度。