基于磁致伸缩效应的声表面波电流传感器敏感机理分析
2017-09-22贾雅娜
贾雅娜,王 文
(1.中国科学院大学,北京 100049;2.声学微机电实验室,中国科学院声学研究所,北京 100190)
基于磁致伸缩效应的声表面波电流传感器敏感机理分析
贾雅娜1,2,王 文2*
(1.中国科学院大学,北京 100049;2.声学微机电实验室,中国科学院声学研究所,北京 100190)
为实现高灵敏度、低温漂的高性能电流传感器,提出将声表面波技术与磁致伸缩效应相结合的电流检测方法,分析了其敏感机理并改善其温度特性。这种声表面波电流传感器采用128°YX-LiNbO3作为压电基片,表面覆盖SiO2薄膜来改善器件温度稳定性,并溅射超磁致伸缩TbDyFe薄膜以响应电流。在电流作用下,TbDyFe薄膜会发生磁致伸缩效应和ΔE效应,引起声表面波相速度的改变。结合层状介质中声传播理论,分析了给定电流下层状结构中声表面波的传播特性,特别分析了TbDyFe和SiO2膜厚对传感器响应的影响。计算结果表明,TbDyFe和SiO2薄膜厚度分别为0.5 μm、2 μm时,该声表面波电流传感器具有最大检测灵敏度58.2 kHz/A,有良好温度稳定性和较高的灵敏度,从而为高性能声表面波电流传感器的研制奠定理论基础。
声表面波;电流传感器;磁致伸缩效应;TbDyFe薄膜
具有高灵敏度、高分辨率、良好稳定性与可靠性的高性能电流在线检测技术在智能电网线路检测、电力冶金与轨道交通中供电安全预警与救援、工业自动化中电源继电保护等领域有着迫切需求[1]。相对于目前成熟的电流传感器如霍尔、光纤型电流传感器,声表面波SAW(Surface Acoustic Wave)电流传感器具有快速响应、结构简单、抗干扰能力强、使用寿命长以及体积小等特点,特别是可以实现无线无源的电流检测手段,大大提高了系统安全性,在上述领域极具工程应用前景和重大的学术价值[2]。2000年,德国弗莱堡大学的Leonhard Reindl和R.Steindl等人将声表面波技术与磁阻效应结合应用于电流测量中,目前已经实验获得了在-800 A到800 A的大电流检测范围内检测精度为5%的无线无源声表面波电流传感器[3-5]。但是从目前的实验报道来看,这种声表面波与磁阻效应结合的电流检测技术在灵敏度与温度稳定性等方面还遇到一些瓶颈问题。首先,基于磁阻效应的磁敏材料在大电流检测中磁场敏感度不够高,传感器采用SAW器件时域幅度响应来作为传感量,导致电流检测的灵敏度及精度不高。此外,缺乏环境温度变化的补偿方法、物理功能结构的优化设计以及传感机理模型的系统性认知,导致目前SAW技术离实用化距离甚远。而近来,稀土型超磁致伸缩TbDyFe薄膜作为一种新型的功能膜材料,具有器件微型化、磁致伸缩系数大、位移量大、能量转换效率高、响应速度快以及非接触式驱动等优良性能[6],因此应用于许多微传感器和执行器的设计,特别是用于高精度磁场的测量,为MEMS系统的开发设计提供了很多技术支持[7-8]。此外,电流传感器的应用环境相对比较复杂,特别是环境温度变化的影响巨大,而目前的传感器为改善检测灵敏度而采用LiNbO3等高压电系数的晶体材料,但是伴随而来的是很高的温度系数(128°YX-LiNbO3一阶温度系数达到了-75 ppm/℃)[7],严重影响到了传感器本身的温度稳定性。Tomar等的研究成果表明:在压电基片表面覆盖与其温度系数极性相反的薄膜材料,通过控制薄膜膜厚可以改善器件的温度稳定性,甚至达到零温度系数[8]。
本文正是采用超磁致伸缩TbDyFe薄膜作为磁敏感膜,以SiO2薄膜作为LiNbO3压电晶体的温度补偿层,设计结合磁致伸缩效应的声表面波电流传感器。结合层状介质中声传播理论,分析了SiO2/128°YX-LiNbO3压电基片器件的温度特性,提取出趋于零温度系数的结构参数;并对TbDyFe薄膜/SiO2/压电基片层状结构中SAW的传播特性进行分析,获得被测电流强度与SAW传播速度的关联特性,特别分析TbDyFe和SiO2膜厚对传感器响应的影响,综合确定出优化的TbDyFe以及SiO2膜厚条件。
1 理论分析
1.1覆盖SiO2温度补偿层的SAW器件温度特性分析
在图1所示的结构中,基片为半无限压电晶体128°YX-LiNbO3,上面覆盖与其温度系数极性相反的SiO2薄膜,厚度为h1。建立如图1所示的层状分析模型[9],其中x1轴与SAW传播方向平行,x2轴与SAW波阵面平行,x3轴为压电基片的法线方向,叉指换能器位于压电基片与的分界面x3=0处,且其指条平行于x2轴。
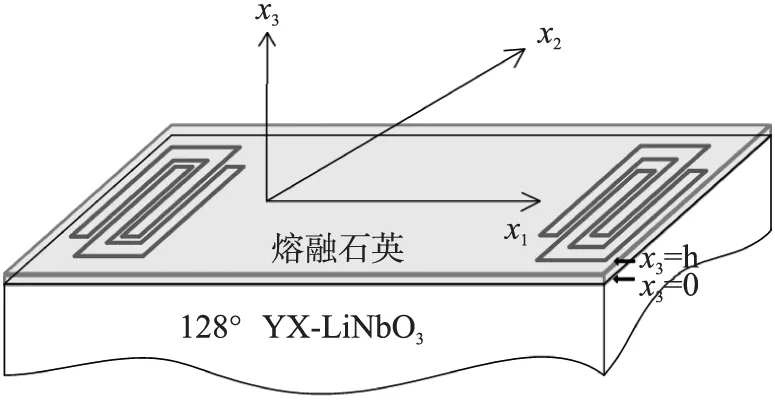
图1 SiO2/128°YX-LiNbO3层状结构模型
SiO2薄膜和LiNbO3压电晶体的材料参数及温度系数列于表1。

表1 各材料参数及一阶温度系数[8]
下面分别分析压电基片和SiO2薄膜层的声波波动方程,并用Ⅰ、Ⅱ区分这两层介质的解。
首先对压电基片中声波的传播模式进行分析,其耦合波动方程为[10]:
(1)
式中:i,j,k,l=1,2,3,c,e,ε分别是128°YX-LiNbO3的弹性系数矩阵、压电常数、介电常数张量,为密度,ui为位移,φ为电势。设耦合波动方程的形式子波解为:
(2)
式中:ks=ωs为表面波波矢,vs为表面波传播速度,s=1/vs为表面波慢度,αI为声波在x3方向的衰减因子。
将式(2)代入耦合波动方程中,得到压电基片的Christoffel方程[11]:
(3)

(4)
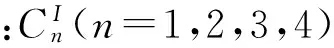
下面分析SiO2薄膜中声波的传播模式,这里采用熔融石英薄层(各向同性SiO2),薄膜中的声波方程为:
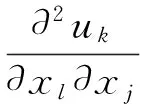
(5)
式中:i,j,k,l=1,2,3。c是SiO2薄膜的弹性系数矩阵,ρ为密度,ui为位移。
设各向同性声波方程的形式子波解为
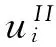
(6)
将式(6)代入声波方程中,得到SiO2薄膜的Christoffel方程:
(7)

(8)
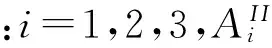
在0
(9)
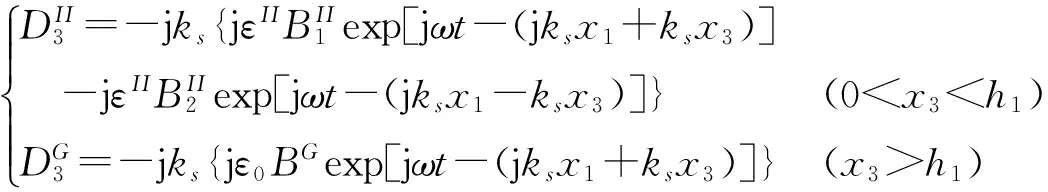
(10)
式中:εII和ε0分别是SiO2和空气的介电常数,ε0=8.854×10-12F/m。同时,设x3=0表面叉指电极的自由电荷密度为σ(x1),忽略叉指电极带来的力学边界影响。则层状结构的边界条件包括:
(1)在x3=0处,应力、位移以及电势各分量连续,边界条件为
(11)
(2)在SiO2薄膜表面x3=h1处,应力法向分量为0,电势及电位移分量连续,边界条件为
(12)
边界条件的矩阵形式如下,它由13个未知数和13个方程构成:
(13)
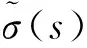
方程组式(13)是非齐次的,直接求解非常困难,因此,我们采用有效介电常数的方法来间接地求解层状介质结构中的声场。定义在x3=0的边界处,有效介电常数为[12-13]:

(14)
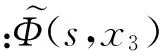

(15)
式中:Ξ8n是系数行列式中元素ξ8n=σ(s)/j2πfs的代数余子式。那么,方程组式(13)有唯一解
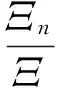
(16)
由边界条件可知
(17)
将式(16)和式(17)同时代入式(14)中,得有效介电常数

(18)
根据式(18),可以对不同的慢度s求出对应εs(s)值,得到一条表面有效介电常数εs(s)曲线。εs(s)是一个复数,其实部的极大值对应的慢度sm表示x3=0处金属化的情况;其实部的过零点对应的慢度sf表示x3=0处自由的情况。根据慢度与速度之间的关系vs=s-1,可得分别对应x3=0处的SAW自由表面和金属表面相速度vm和vf[14-15]。
下面对SiO2/128°YX-LiNbO3压电基片器件的温度特性进行分析。
压电基片和SiO2薄膜的材料特性会随着温度不同发生变化,因此将经过温度修正的材料参数代入方程组式(13),即可得到不同温度下的SAW相速度,根据延迟温度系数TCD(Temperature Coefficient of Delay)的表达式[8]:
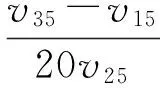
(19)
式中:α为压电基片的热膨胀系数,可以求得器件的延迟温度系数。v15,v25,v35分别是温度为15 ℃、25 ℃、35 ℃时SAW相速度。各材料参数随温度的变化可以近似成如下关系:
X=X0[1+α1(T-T0)]
(20)
式中:X和X0分别是温度为T和T0时材料参数,a1是材料的一阶温度系数。利用机电耦合系数的表达式[8]:

(21)
可以计算出覆盖SiO2温度补偿层的SAW器件机电耦合系数。
1.2 声表面波电流传感器敏感机理分析
采用射频磁控溅射技术在SiO2薄膜表面溅射超磁致伸缩TbDyFe薄膜,在待测电流产生磁场的作用下,TbDyFe薄膜会发生磁致伸缩效应和IE效应,使薄膜的尺寸和杨氏弹性模量发生改变,从而使得SAW相速度发生相应变化,并导致振荡器频率发生改变,并以此表征被测电流的大小。
计算中采用非晶态超磁致伸缩TbDyFe薄膜,它是各向同性材料,表2列出其部分物理参数。

表2 TbDyFe薄膜部分物理参数[16]
非晶态TbDyFe薄膜在外磁场作用下的磁致伸缩效应为各向异性,即沿长度方向磁化时,薄膜产生的应变为[17-18]:
ε1=-2ε2=-2ε3=λ
(22)
式中:εi是TbDyFe薄膜沿xi方向的应变(i=1,2,3),λ是薄膜的磁致伸缩系数,与外部磁场强度有关。因此,磁致伸缩效应引起TbDyFe薄膜厚度h和密度ρ发生如下改变:
(23)
式中:m是薄膜的质量,a0、b0、h0分别是待测电流强度为0时薄膜的初始长度、宽度和厚度。
同样,TbDyFe薄膜的IE效应也会引起弹性系数矩阵cIJ的改变[13]:
(24)
式中:u是TbDyFe薄膜的泊松比,一般不随电流变化,取为0.3[18],E是薄膜的杨氏弹性模量,与外部磁场强度有关。
对TbDyFe薄膜/SiO2/压电基片结构,建立如图2所示的层状分析模型,并采用有效介电常数方法求解SAW相速度。SiO2和TbDyFe薄膜的厚度分别为h1和h2。

图2 TbDyFe薄膜/SiO2/压电基片层状结构模型
上一小节分析了层状结构中128°YX-LiNbO3压电基片与SiO2薄膜的声波传播模式,下面对非晶态TbDyFe薄膜层的声波波动方程进行分析,并用III来表示。
同理根据各向同性固体中的声波方程,TbDyFe薄膜层中声波位移解、电势以及电位移为:
(25)

TbDyFe薄膜/SiO2/压电基片层状结构的边界条件除式(11)外,还包括:
①在SiO2薄膜表面x3=h1处,应力、位移、电势及电位移各分量连续,边界条件为
(26)
②在TbDyFe薄膜表面x3=h1+h2处,应力法向分量为0,电势及电位移分量连续,边界条件为
(27)
以上边界条件由21个未知数和21个方程构成,其矩阵形式如下:
(28)
同样利用有效介电常数方法求解该非齐次方程组,可以得到相应的有效介电常数εs(s)曲线,根据εs(s)实部的零、极点所对应的慢度值,可以求得TbDyFe薄膜/SiO2/128°YX-LiNbO3压电基片层状结构中SAW自由表面和金属表面相速度vf和vm(求解过程与上节类似)。
再利用TbDyFe薄膜的磁致伸缩曲线和IE曲线得到不同磁场强度下薄膜的磁致伸缩系数和杨氏弹性模量E,把薄膜厚度、密度以及弹性系数矩阵的改变量代入式(28),即可求得不同磁场强度下层状结构中SAW相速度。
2 SAW电流传感器温度特性及敏感机理计算结果分析
本文计算了SAW器件延迟温度系数和机电耦合系数随SiO2温度补偿层厚度的变化规律,如图3、图4所示,以及不同磁场强度下SAW相速度随SiO2和TbDyFe薄膜厚度的关系曲线,以提取出SAW电流传感器的最优结构参数,如图5、图6所示,最后给出最优参数下SAW相速度随待测电流强度的变化曲线。

图3 SAW器件TCD与SiO2厚度h1的关系曲线
图3、图4给出SiO2薄膜厚度在[0,5 μm]区间时,SAW器件延迟温度系数以及机电耦合系数的变化规律。从图3可以看出,SiO2膜厚对器件TCD影响显著,随着SiO2膜厚的增加,器件TCD逐渐减小,当h1=2.7 μm时,器件TCD为零。图4中,随着SiO2厚度的增加,机电耦合系数K2先增后减,在h1=1.5 μ m处达到最大值0.065。综合SiO2膜厚对器件延迟温度系数和机电耦合系数的影响,在以下的计算中选择h1=2 μm,此时器件TCD为18 ppm/℃,K2=0.064 4,具有较好的温度特性和较大的机电耦合系数。

图4 SAW器件机电耦合系数K2与SiO2厚度h1的关系曲线
图5、图6计算得到当磁场强度分别是0、100 Oe、200 Oe时,SAW的相速度随TbDyFe和SiO2膜厚的变化曲线。图6给出TbDyFe薄膜厚度在[0,1 μm]区间时,SAW相速度的变化曲线。
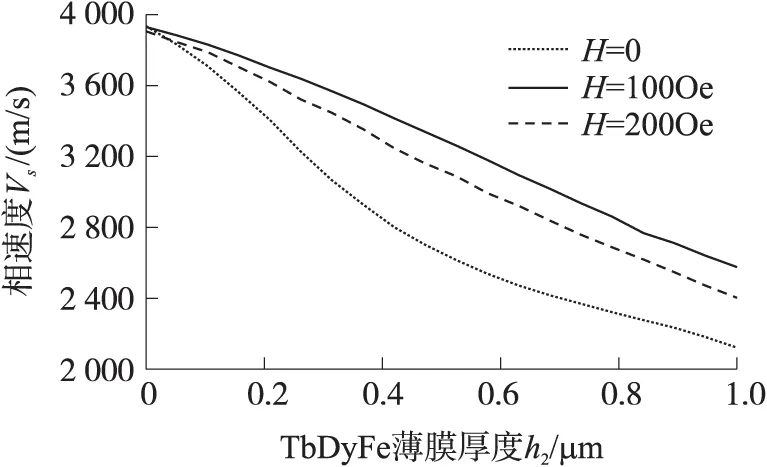
图5 SAW相速度vs与TbDyFe厚度h2的关系曲线
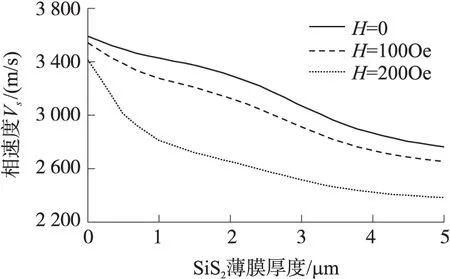
图6 SAW相速度vs与SiO2厚度h1的关系曲线
由图5可知,当TbDyFe薄膜厚度增加时,不同磁场强度所对应SAW相速度的差值是先增大后减小的趋势,综合考虑,选取TbDyFe薄膜厚度h2=0.5 μm,此时SAW电流传感器具有较高灵敏度。同样,图6给出当SiO2薄膜厚度在[0,5 μm]区间时,不同磁场强度下SAW相速度的变化曲线。
由图6可知,当SiO2薄膜厚度增加时,不同磁场强度所对应SAW相速度的差值也是先增大后减小的趋势,综合图3、图4中SiO2膜厚对SAW器件延迟温度系数和机电耦合系数的影响,选取SiO2薄膜厚h1=2 μm。
毕奥萨伐尔定律H=I/2πr给出无限长直导线的电流与磁场强度的关系,其中H、I分别是磁场强度和电流强度,r是被测点与导线的垂直距离[19-20]。图7是SAW电流传感器在最优结构参数下,即h1=2 μm,h2=0.5 μm,相速度随无限长直导线内电流强度的变化曲线,此时电流强度在0~1 000 A范围内,被测点与直导线的垂直距离取r=1 cm。从图7可以看出,随着电流强度的增加,SAW相速度单调递减,相速度与电流强度呈近似线性关系。此时电流传感器的最大灵敏度可达到58.2 kHz/A,理论实现了对电流强度大范围、高灵敏度、高准确性的测量。

图7 SAW相速度vs与被测电流强度的关系曲线
3 结论
本文提出一种结合磁致伸缩效应的新型声表面波电流传感器,采用超磁致伸缩TbDyFe薄膜作为敏感膜,利用TbDyFe薄膜在磁场作用下巨大的磁致伸缩效应和IE效应,以实现对电流高灵敏度、高准确性的测量,并采用温度系数极性与LiNbO3压电基片相反的SiO2薄膜对器件的温度特性进行改善。基于层状介质中声波传播理论,对这种新型声表面波电流传感器的温度特性和敏感机理进行了分析,特别分析了TbDyFe薄膜和SiO2温度补偿层厚度对传感器响应的影响,综合确定出优化的TbDyFe和SiO2膜厚条件。计算结果表明,在最优结构参数下,这种基于磁致伸缩效应的声表面波电流传感器延迟温度系数(TCD)为18 ppm/℃,最大检测灵敏度可达到58.2 kHz/A,具有良好温度稳定性和较高的灵敏度。理论实现了对电流强度大范围、高灵敏度、高准确性的测量,为这种高性能SAW电流传感器的实验研究提供了理论支持。后续实验将TbDyFe薄膜作为敏感膜,通过射频磁控溅射镀在高性能、低损耗的SAW器件表面,并结合相关振荡电路构成SAW电流传感器,通过赫姆霍兹驱动线圈对其进行实验验证。
[1] 吕英俊,李静. 电力系统中电子式互感器的研究[J]. 煤矿机械,2005(10):34-36.
[2] 张华伟,孙越强. 几种非侵入式电流测量技术[J]. 现代电子技术,2005,28(21):80-83.
[3] Leonhard Reindl,Gerd Scholl,Thomas Ostertag,et al. Theory and Application of Passive SAW Radio Transponders as Sensors[J]. IEEE Transactions on Ultrasonics,Ferroelectrics and Frequency Control,1998,45(5):1281-1292.
[4] Steindl R,Hausleimer C,Hauser H,et al. Wireless Magnetic Field Sensor Employing SAW-Transponder. Applications of Ferroelectrics,2000. ISAF 2000. Proceedings of the 2000 12th IEEE International Symposium on,2(2000):855-858.
[5] Leonhard Reindl. Wireless Passive SAW Identification Marks and Sensors. 2nd Int. Symp. Acoustic Wave Devices for Future Mobile Communication Systems,Chiba Univ. 3rd-5th March,2004:1-12.
[6] 李秀. 超磁致伸缩薄膜的力学特性以及实验研究[D]. 大连:大连理工大学机械制造及其自动化学院,2009.
[7] 王仪. 超磁致伸缩材料的微位移执行器研究[D]. 镇江:江苏大学机械工程学院,2016.
[8] 卢诗华,于歆杰,楼国锋. 一种基于磁电层合材料的新结构大电流传感器[J]. 电工技术学报,2016,31(23):70-76.
[9] 潘峰. 声表面波材料与器件[M]. 北京:科学出版社,2012.
[10] Tomar M,Gupta V,Mansingh A. Temperature Stability of c-Axis Oriented LiNbO3/SiO2/Si Thin Film Layered Structures[J]. J Phys D:Appl. Phys,2001,34:2267-2273.
[11] 邵秀婷,王文. 结合金属膜的YZ-LiNbO3压电基片上声表面波陀螺效应分析[J]. 传感技术学报,2013,26(3):315-318.
[12] Solie L. Piezoelectric Waves on Layered Substrates[J]. Journal of Applied Physics,2003;44,(2):619-627.
[13] Milsom R F,Reilly N,Redwood M. Analysis of Generation and Detection of Surface and Bulk Acoustic Waves by Interdigital Transducers[J]. IEEE Transactions on Sonics and Ultrasonics,1977,24(3):147-164.
[14] Auld BA. 固体中的声场和波:上册[M]. 孙承平,译. 北京:科学出版社,1982:352-375.
[15] 胡浩亮,王文,何世堂,等. 一种采用穴番-A敏感膜的新型声表面波瓦斯传感器的研究[J]. 传感技术学报,2016,29(2):166-170.
[16] 陈磊. Tb<,0.27>Dy<,0.73>Fe<,2>薄膜超快光学与电子动力学特性实验研究[D]. 镇江:江苏大学,2007.
[17] 张昌盛. 磁热感生各向异性对超磁致伸缩材料的作用研究[D]. 杭州:浙江大学材料科学与工程学系,2012.
[18] 万红. TbDyFe薄膜的磁致伸缩性能及其与弹性、压电衬底复合效应研究[D]. 长沙:国防科技大学材料科学与工程学院,2005.
[19] 武一,李奎,王尧,等. 磁调制式剩余电流传感器的动态励磁过程分析与仿真[J]. 电工技术报,2014,29(7):244-252.
[20] 刘磊,范涛,李貅,等. 均匀半空间回线源非中心点频率域电磁场计算[J]. 物探化痰计算技术,2014(5):555-559.

贾雅娜(1991-),女,中国科学院声学研究所博士研究生,研究方向为声表面波电流传感器,jiayana225@163.com;

王文(1976-),男,博士,中科院声学所研究员,博导,德国洪堡学者,2011年入选中科院“百人计划”,2016年入选“中科院特聘研究员”骨干人才。主要从事微声学传感技术研究,承担国家及省部级科研项目20余项。发表论文160余篇,其中SCI收录50篇,EI收录80余篇。授权专利19项。出版专著2部,wangwenwq@mail.ioa.ac.cn。
TheSensitiveMechanismofSAWCurrentSensorBasedontheMagnetomechanicsEffect
JIAYana1,2,WANGWen2*
(1.University of Chinese Academy of Sciences,Beijing 100049,China;2.State Key Lab. of Acoustics,Institute of acoustics,Beijing 100190,China)
In order to achieve a kind of high-performance current sensor with high sensitivity and low temperature drift,this paper put forward a kind of new current detection method combined the surface acoustic wave(SAW)technology with magnetostrictive effect,analyzed its sensitive mechanism and improved its temperature characteristic.This SAW current sensor used 128°YX-LiNbO3as piezoelectric substrate,and SiO2film whose temperature coefficient polarity is opposite to improve the temperature stability,and one of the SAW delay lines was sputtered with giant magneto strictive TbDyFe film to detect current. The applied current induces the TbDyFe film’s magneto strictive strain and ΔEeffect,changes the SAW propagation characteristics. Based on the theory of acousticwave propagation in layered medium,this paper analyzed the SAW propagation characteristics in the TbDyFe film/SiO2/piezoelectric substrate layered structure under given current conditions,especially analyzed the effects of TbDyFe and SiO2film thicknesson sensor response. The results show that the highest sensitivity can reaches 58.2 kHz/A when the TbDyFe and SiO2thin film thickness are respectively 0.5 μm and 2 μm,which shows excellent temperature stability and high sensitivity.
SAW;current sensor;magneto mechanics effect;TbDyFe film
2016-10-09修改日期:2017-06-06
TP212.1
:A
:1004-1699(2017)09-1310-08
10.3969/j.issn.1004-1699.2017.09.002
