融合电磁超声载波的声发射传播特性分析*

蔡智超,张 闯

(1.华东交通大学电气与自动化工程学院,南昌 330013;2.河北工业大学电磁场与电器可靠性省部共建重点实验室,天津 300130)

融合电磁超声载波的声发射传播特性分析*

蔡智超1*,张 闯2

(1.华东交通大学电气与自动化工程学院,南昌 330013;2.河北工业大学电磁场与电器可靠性省部共建重点实验室,天津 300130)

电磁声发射是通过对缺陷导电结构件施加非接触式电磁载荷,进而激发声发射应力波,并据此效应来进行构件无损检测。本文针对电磁声发射信号不适合较远距离传播问题,融合电磁超声技术,实现对声发射应力波的载波远距离传输。文章首先从自由电子运动理论出发,从微观层面上研究电流对金属位错激活能的影响,推导出定向漂移的自由电子与位错碰撞时所产生的能量交换;其次搭建了融合电磁超声载波的电磁声发射有限元模型,分析了多个特征源激励下的应力波传播位移;最后利用希尔伯特黄变换方法对载波实验信号进行了分析比较。本文通过对传统的电磁声发射激励端研究、改进,提升电磁超声对电磁声发射应力波的传输特性,拓宽了电磁声发射检测的应用范围。

电磁声发射;电磁超声;融合;载波;传播特性

循环型失效是承压型结构的主要失效模式,同时在加工以及制造过程中存在各类缺陷,在工况循环载荷作用下,极易产生疲劳裂纹进而影响整体结构的疲劳寿命,由此可能引发灾难性的事故[1]。因此对于循环载荷作用下所含缺陷设备的安全性的检测评估尤为重要。其中电磁声发射技术使用局部的电磁激励代替了声发射传统的整体加载,避免对完好区域造成损伤以及非检测区域噪声信号的干扰,可利用这一特性对特定区域的缺陷进行甄别。因此该方法对于萌生的疲劳裂纹、瞬时故障有较好的检测能力[2-4],该方法兼顾声发射对动态裂纹检测的高效率以及电磁无损检测的非接触、无需耦合剂、恶劣环境下局部加载等独特优势。

然而,电磁声发射检测裂纹研究中存在两个问题:一是电磁加载过程中应区分电磁激励所产生的弹性超声波与电磁声发射应力波;二是电磁声发射信号非常微弱,并不适合于远距离传输,存在着未传达至接收换能器时便已衰减的问题。因此为了传输、获取、区分所评价结构件性能和缺陷状态的声发射信号,且保证原始信号的完整性,本文选择融合电磁超声载波的电磁声发射方法,旨在探索融合检测方式对疲劳损伤检测的可行性。

融合电磁超声载波的电磁声发射源于传统的声-超声技术[5-6],同样也具备评估弥散缺陷分布以及材料力学性质变化等基础应用能力,并且集电磁超声和电磁声发射技术特点于一身:如图1所示,利用复合线圈在被测表面感应涡流,由于缺陷边界的存在对表面涡流分布造成一定的影响,并在裂纹尖端处产生涡流集中效应,基于电致塑性效应将在该处激励电磁声发射信号;同样基于电磁-结构耦合换能原理在电磁线圈正下方涡流区域也将产生振动的超声弹性波[7]。因此,在同时激发超声波与声发射应力波两种声波的前提下,利用超声波携带声发射信号完成远距离传输过程,提高声波传输效率以实现对疲劳裂纹评估。

图1 融合检测中电磁声发射模型图

本文从自由电子理论出发分析电磁声发射机理,利用有限元方法实现对电磁超声载波过程比较、分析、计算试块中声波的传播过程以及超声波载波情况。制作含疲劳裂纹的损伤试件,设计了电磁检测线圈及融合电磁超声载波的电磁声发射实验,并基于希尔伯特黄方法对实验过程中所采集到的应力波信号进行特征分析,探究不同频率下超声的载波效率等问题。

1 基于自由电子理论的电磁声发射分析

瞬时高密度电流作为一种附加注入能量将对原子的随机运动将产生影响,促进原子扩散能力,推动位错运动(滑移、攀移),美国Conrad学者将定向运动电子与不规则原子排列产生的位错作用情况定义为电子风力[8-9]。

在电子风力的作用下,位错的自由端绕扎钉中心旋转,直至位错线方向与电流方向平行,此时电子风力对位错的作用最小。漂移电子通过碰撞使得电子的自身能量转移至位错,并增强了位错运动,即位错运动与漂移电子运动方向有关,同样外加静磁场能对位错运动方向产生影响。所以从自由电子层面研究有利于分析电磁加载对金属位错的具体影响,能更直观地得出施加的电磁载荷参量与声发射之间的关系。

导体晶体结构并非完美,或多或少会存在晶体缺陷、空位、位错、杂质等,这些将散射漂移电子。常温中原子依然存在热运动,其将在晶格位置上下振动。漂移电子无法避免与这些振动的原子相碰撞,而被振动的晶格散射并做无规则随机运动,即在无电场的情况下漂移电子在任何方向都不会显示任何净位移。如存在一个固定电场,漂移电子会与振动的原子突然碰撞并损失部分动能,但由于电场力的存在,其在围绕固定方向上做加速运动,并不断与该区域上的原子撞击,这种电子传递的方式会使运动方向及能量发生改变,从而获得与场强相关的稳定漂移速率,虽然运动路径是曲折的,但在宏观上表现为定向运动。

当电子受x方向电场Ex作用下的漂移速率vdx,假设该方向第i个漂移电子受电场作用在ti时刻与某一原子发生碰撞,碰撞后瞬时速度为uxi,在电场力作用下以加速度eEx/me经过(t-ti)时间,在t时刻产生的瞬时速率vxi为:

(1)

式中:e为单个电子电荷,me为单个电子质量。

式(1)是针对某一电子而言的速率分析,如若考虑总数为N个电子进行速率平均可得:

(2)

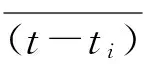
(3)

式中:μd=eτ/me为迁移率,作为电子常数,其与电子平均散射时间τ有直接的关系,晶格振动、晶体缺陷和杂质等的存在也会影响τ的变化。显然针对于相同的材料而言,在结构不发生任何变化的情况,其迁移率是个恒定值。由式(3)可知电场强度越大,漂移速率也越大。

(4)

式中:n为导体内单位电子数目,d表示密度,Mst指代单位体积原子总质量,NA为单位体积原子个数。

导带中电子平均速度u达到106m/s,因此在极高的工作电流(～107A/mm2)或电压(～102kV/m)加载情况下,其引起的漂移速率远小于电子的平均速度。所以当电场作用于一个导体时,实际上其平均速率并不受影响。电场的加载并不能改变电子平均速率,即加强电场幅值不能改变电子热运动过程,从另外一个侧面也就说明了焦耳热效应在电致塑性过程中的作用极低。漂移电子与原子碰撞的激烈程度未变,电子所具有的动能并未发生明显变化。

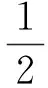
(5)

当漂移电子在其运动路径上与晶体缺陷内大量位错交互时,弛豫时间τ将变小,漂移电子会更为集聚,则单位时间内漂移电子与位错区域中原子的碰撞几率zE=1/τ将明显增大。则单位时间内位错区域从漂移电子中获得的能量更为集中。

(6)

式中:PE≫P=zW,z表示单位时间内每个自由电子与位错碰撞的次数,P则代表了单位时间单个位错从自由电子获得的能量。式(6)中NE为单位时间撞击位错区域的电子浓度。

(7)

由式(7)可得电场的作用强度越大,其在单位时间内撞击位错区域的电子浓度就会越高。

因此在施加电场情况下,电子与构成位错的原子相碰撞,位错结构中的原子将获得能量:瞬时高幅值电场加载,伴随着原子在短时间内与大量漂移电子的撞击,位错原子将瞬间积累强大的能量。位错原子所获得集中的电子转移的能量能够克服势垒障碍,促使位错滑移。若形成晶格位错的原子平均数为M,则在单位时间内电场产生的漂移电子作用于位错的总能量为:

PT=MPE

(8)

式(8)为转移至位错的总能量,形成电磁加载后的激活能。因此基于经典自由电子理论可定性地给出电场作用强度与电磁声发射的直接关系:①导体的迁移率越大,更易实现漂移电子的运动,电子在移动过程中与位错的碰撞频率将增大,传递给位错的能量就越大;②电场实现了漂移电子的定向移动,使得电子的运动路径与位错发生交叉;漂移电子的集聚,实现大量数目漂移电子与位错之间的能量转换;③增强电场推动电子的漂移速率以改变单位时间内作用于位错的数目。同时晶格位错的数目增加也会缩短弛豫时间,增加每单位时间的碰撞几率;④电场的加载时间持续必然体现位错能量的积累,这个期间产生焦耳热现象将增强原子自身的振动频率,改变弛豫时间,进而提高转换能量的累积。

故在电磁声发射过程中,源于能量转换的电子风力及长时间加载的焦耳热效应是相互关联,并且与缺陷属性、电磁加载条件等紧密相关。

图2 融合检测中电磁声发射有限元模型

2 融合检测声场有限元计算

融合检测中电磁声发射检测有限元模型,如图2所示,U型永磁铁两极头使用型号为N35的钕铁硼,其剩磁为y轴方向1.2 T,极头中间放置铁氧体。选择500 kHz控制频率复合线圈如图1所示,电磁线圈通以持续时间为87.5 μs的500 kHz正弦周期50 A电流,交变磁场以及静磁场共同作用所产生的洛伦兹力设定为结构场的体力载荷,对金属表面固定点施加特定函数作用力以实现电磁声发射载荷的模拟。

真实电磁声发射信号具有中心频率、较宽的信号频带以及极短的持续时间等特点。因此,利用高斯窗函数调制扫频信号进行近似描述,其控制方程为:

(9)

式中:A为信号幅值,fs为信号下限截止频率,B为信号频带宽度,T为信号瞬时持续时间。针对此模型设计模拟声发射信号fs=275 kHz、B=50 kHz,即信号频率范围为275 kHz～325 kHz,其中心频率为300 kHz,持续时间T=87.5 μs,宽带系数α=2×109s-2,时间系数τ=40 μs,下限截止频率修正系数β=0.73,信号频带宽度修正系数η=0.25。模拟电磁声发射函数波形图及频谱图如图3、图4所示。

图3 电磁声发射源函数F(t)

图4 电磁声发射源函数F(t)频谱

在换能区域(趋肤区域)对网格进行三层以上的网格剖分,在声场传播区域最大网格尺寸设定为表面波波长的1/4,以此保证求解计算的准确性和稳定性。

经过对有限元模型瞬态求解之后,电磁线圈所产生的超声波面外位移如图5所示。随着传播时间的增加,表面波位移衰减较慢,而体波位移衰减较快。

2.1 声波位移分析

为分析应力波的传播效果,对比3种激励源,如表1所示。可以求解距离发射复合线圈150 mm质点处应力波产生的声波面外位移分量OP(Out-Plane Displacement)和面内位移分量IP(In-Plane displacement)。该处质点位移包括微弱的横波成份和丰富的表面波成份,并且表面波IP比表面波OP相位超前π/2。

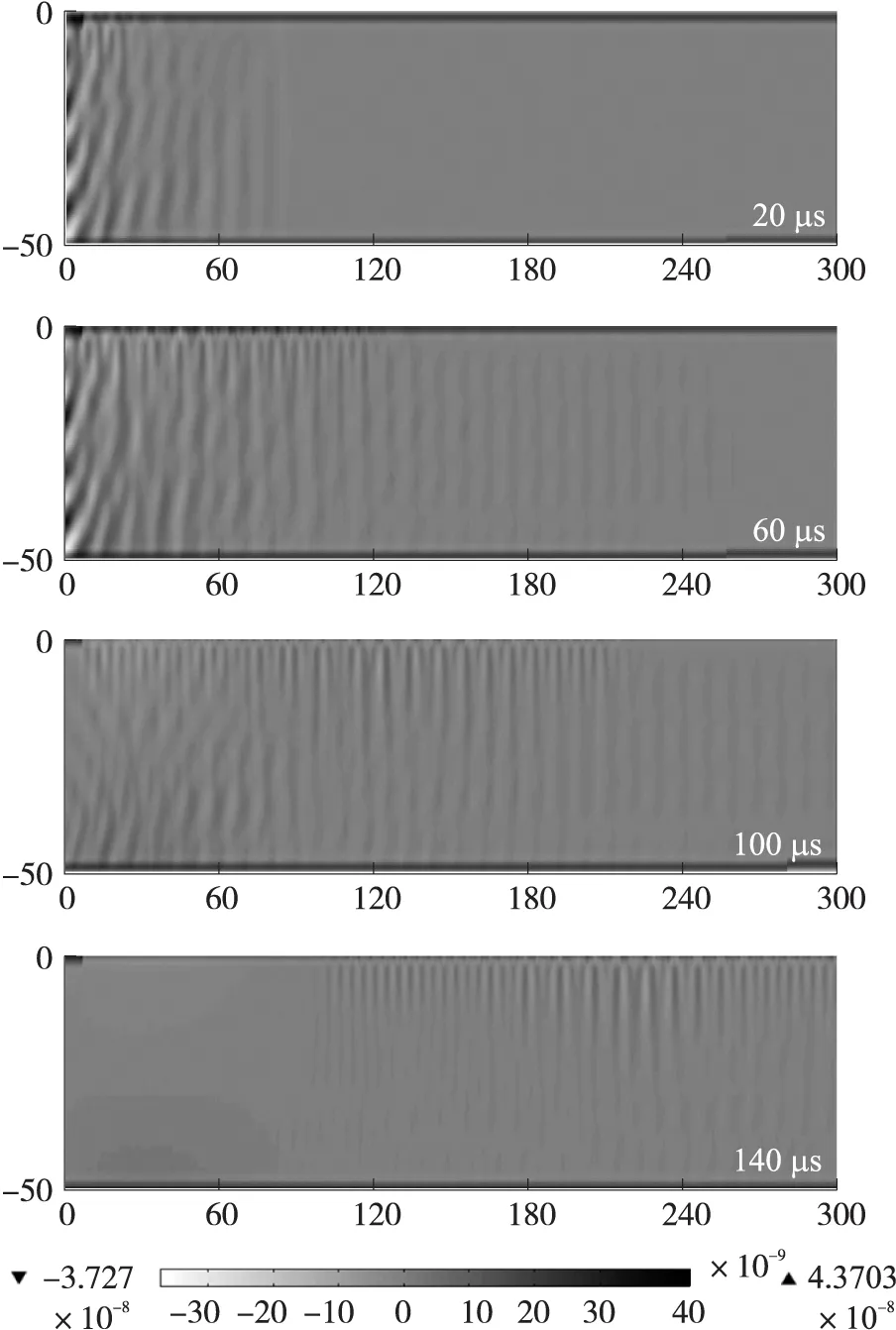
图5 不同时刻铝板中声波面外位移分布图

激励源描述F(t)(简称F)声场信号仅为声发射F(t)+螺旋线圈产生的超声波(简称FSC)声场信号为声发射与螺旋线圈产生的少量超声波F(t)+电磁线圈产生的超声波(简称FCC)声场信号为声发射与电磁线圈产生的丰富超声波

“F”激励源以模拟真实反演裂纹尖端的声发射信号,其所产生的表面位移频段为275 kHz～325 kHz,但是其位移最高幅值10-11mm,最为先进的声发射换能器也仅能采集到10-12mm幅值的信号。但是所采集的声发射信号将受噪声干扰,同时初始、末尾两端微弱的声发射信号将不易采集,如图6(a)所示。然而长距离的声波传输严重影响声发射信号特征的提取,降低声发射频带宽度。

利用“FSC”来模拟传统的电磁声发射信号,其常由单独的螺形线圈施以电磁载荷,然而该过程也将引入超声弹性波,如图6(c)、图6(d)所示,但其引入的超声幅值较低,与被载的声发射信号幅值几近相当,虽能提高应力波的传播距离,实现部分的载波效应,但所采集到声波依然十分微弱,载波效果不显著。对于电磁线圈激励,由于其比传统的电磁声发射激励线圈增加了蛇形侧“FCC”,线圈结构如图9所示,因此这将产生丰富的指向性超声波,其IP及OP将接近到10-10mm,如图6(e)、图6(f)所示,因此增加蛇形侧的电磁线圈能更好的提高载波效率。

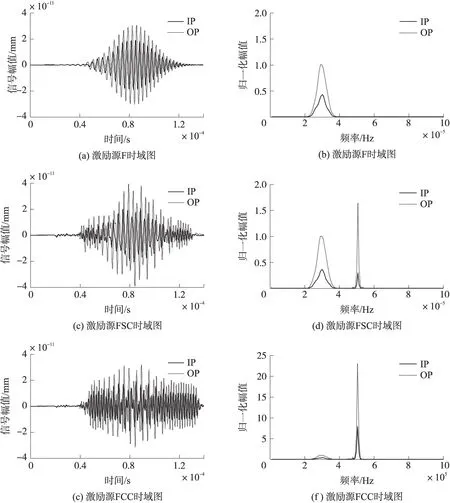
图6 固定点的面内及面外位移及FFT分解

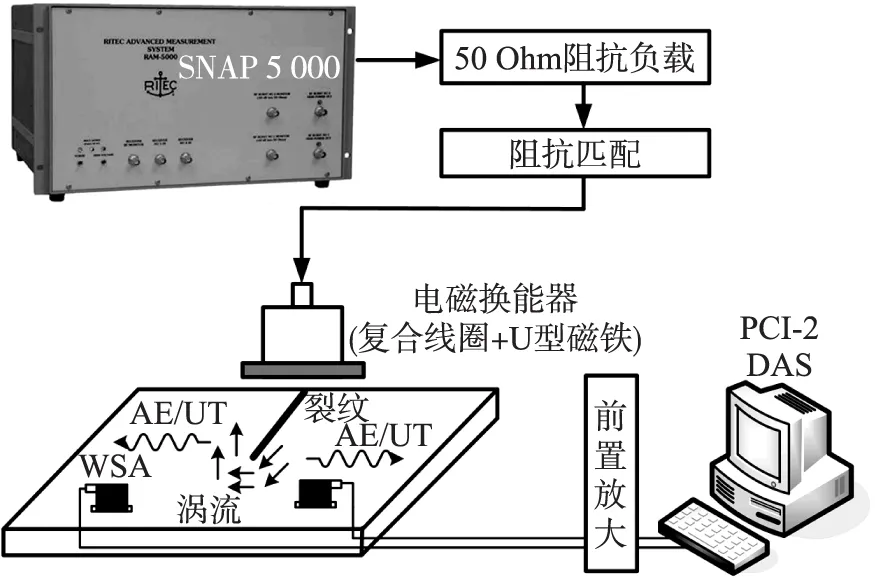
图7 实验系统原理框图

3 电磁声发射检测实验研究及信号分析

图8 含疲劳裂纹的损伤试件

复合检测实验系统如图7所示。电磁换能器为复合线圈与U形永磁体组合。传统铝板的声发射集中于0～400 kHz,将激励电流频率选择在500 kHz～1 000 kHz之间,从频谱上以区别电磁声发射信号与电磁超声信号。试件为0.20 m×0.20 m×0.02 m的6061铝块,其中铝块边缘通过线切割制作50 mm预制裂纹,经施加10 kN疲劳载荷,制作长约58 mm的疲劳裂纹,如图8所示。

电磁线圈设计如图9所示,螺旋侧均采用线宽0.5 mm、线高0.035 mm、线间距0.3 mm;蛇形侧采用线宽0.1 mm、线高0.035 mm,线间距可变以满足两相邻线圈所通入电流相位相差π,满足相长干涉叠加条件[7]。复合线圈采用柔性印刷电路板制作,减少提离距离以增大电磁载荷效率。

图9 EMAE换能线圈

以图9(f)电磁线圈为例,通以f=650 kHz的激励电流。采集的时域信号波形如图10(a)所示,所检测信号在时域上由连续的声波组成,在声波前半段波包幅值变化较大,而声波后半段波包幅值相对平稳。对该时域信号进行HHT变换求得边际谱如图10(b)所示,在650 kHz频段附近的声波信号最为强烈,即为电磁-结构换能所产生的超声弹性波为主要贡献,而在50 kHz～150 kHz以及350 kHz～450 kHz低频段所呈现幅值较低、特征频段突出等特点,即为电磁声发射应力波信号为主要贡献。

图10 实验特征信号

文献[10]表明水平磁场下电磁声发射随着频率变化所产生的总能量保持一致,对于相同电流幅值下不同频率的激发其产生的声发射特性差异并不显著,即利用U型磁铁作为水平磁场激励,便可视其产生的电磁声发射信号为恒定的声波信号。

因此需对已采集的应力波信号进行超声波滤波处理,给定原始信号一个500 kHz的低通滤波,再进行特定的信号处理方法:希尔伯特黄HHT(Hilbert-Huang)变换方法对非线性、非平稳信号的声发射信号具有良好的处理能力,能够自适应的时频分解并增强了时频集聚性,降低频谱能量泄露的同时提高了时频分辨率[11-13]。通过希尔伯特黄变换所求解各个本征模态函数IMF分量所占的不同的能量值:

(10)

式中:n表示为电磁声发射信号的长度,该值是由采样长度与预触发值有关,ci(k)代表第i个IMF分量中的第k个元素,每个IMF分量的能量比值为:

Pi=Ei/Et

(11)

式中:Et表示IMF分量的总能量,即为各个Ei之和。

图11 不同激励频率下应力波总能量

按式(11)求解各控制频率线圈激发的声发射信号的总能量Et。如11所示,当对所有设计频段的电磁线圈进行激励如图9所示,图9(d)电磁线圈产生的总能量明显高于其他激励线圈所产生的能量,这是由于450 kHz激励线圈所产生的弹性波频率与声发射特征频率发生重合,该部分的弹性波并未通过低通滤波器滤除,同时其频率混叠将影响声发射信号特征分析,因此该频段并不适用于作为载波频段。本文针对550 kHz～950 kHz频率的电磁激励所采集到的应力波信号进行分析,先滤除500 kHz以上弹性超声波再对声发射应力波进行分析。

通过希尔伯特黄计算可得计算可知信号中95%以上的能量集中于IMF1～IMF 5分量,表2为各个IMF分量对应的频率范围。

表2 IMF分量频带范围

如图12所示,不同的弹性超声波下IMF1分量的Ei值呈相对上升趋势,而其他分量的Ei值趋势并不是十分显著。同样如图13所示,IMF1分量的Pi值呈相对上升趋势,而其他分量的Pi值变化范围在0.05～0.30之间。即特征频段IMF1受载波频率变化最为显著。

图12 不同本征模态函数下Ei值情况

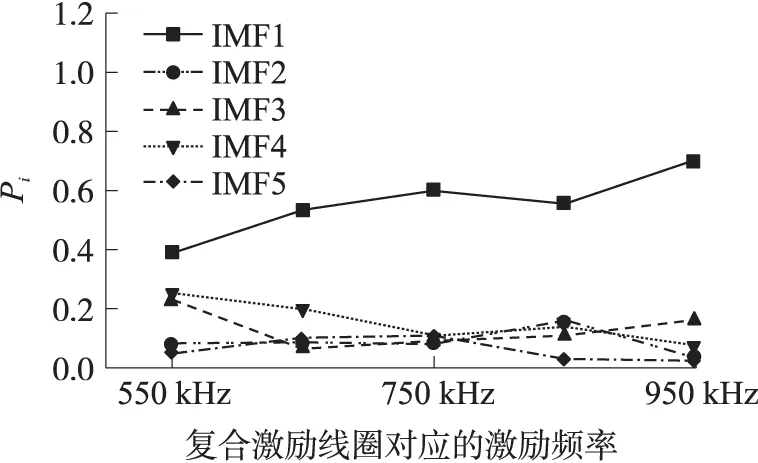
图13 不同本征模态函数下Pi值情况

通过对比分析可以得出:当超声载波与电磁声发射特殊频段相近时,载波效率较低;当载波与电磁声发射特殊频段存在一定频率差时,载波效率较好。这是由于当载波频段与声发射特殊频段相近时,易发生波速混叠,不适合加载声发射信号远距离传输。

5 结论

对融合电磁超声载波的电磁声发射技术进行理论、仿真、实验方面的研究,主要结论如下:①定向电子的自由移动,通过动能的注入激活裂纹尖端位错的运动,实现自由电子与位错之间的能量交换,进而实现位错集聚最为明显的裂纹尖端位错移动并释放应力波信息;②电磁声发射通过电磁线圈的激励必然会引入弹性波,然而通过电磁换能线圈的改进,可在产生电磁声发射的同时激励出指向性超声波这一特性,通过超声载波能力实现对电磁声发射应力波的远距离传输。同时利用适合的频段激励、电磁线圈匹配、滤波等过程能够在接收端实现两种应力波的分离。

[1] 张伯君,业成,张忠政,等. 含裂纹缺陷气瓶疲劳裂纹扩展及寿命预测[J]. 油气储运,2014,10:1061-1065.

[2] Finkel P,Godinez V. Electromagnetic Simulation of Ultrasonic Signal for Nondestructive Detection of Ferromagnetic Inclusions and Flaws[J]. IEEE Transactions on Magnetics,2004,40(4):2179-2181.

[3] 刘素贞,金亮,张闯,等. 电磁声发射检测技术的涡流激励方法[J]. 电工技术学报,2012,27(7):153-159.

[4] 张晓涛,唐力伟,王平,等. 最小周期相关熵解卷积结合窄带解调的轴承复合故障诊断研究[J]. 振动工程学报,2015,28(4):666-672.

[5] 陈振华,卢超,陆铭慧,等. 基于声-超声检测的薄钢板多焊点结构完整性评价技术[J]. 机械工程学报,2013,8(49):57-61.

[6] 尼涛. 时频分析技术在声-超声检测中的应用[J]. 声学技术,2013,32(4):502-505.

[7] 范吉志,吴运新,石文泽,等. 电磁超声换能器线圈设计与提高换能效率研究[J]. 传感技术学报,2016,29(1):29-34.

[8] Lei Guana,Guoyi Tang,Paul K Chu. Recent Advances and Challenges in Electroplastic Manufacturing Processing of Metals[J]Journal of Materials Research,2010,25(7):1215-1224.

[9] Stephen D Antolovich,H Conrad. The Effects of Electric Currents and Fields on Deformation in Metals,Ceramics,and Ionic Materials:An Interpretive Survey[J]. Materials and Manufacturing Processes,2004,19(4):587-610.

[10] 蔡智超,刘素贞,张闯,等. 施加水平磁场下电磁声发射与裂纹指向特征分析[J]. 振动与冲击,2017,36(5):8-14.

[11] Seif E Hamdi,Alain Le Duff,Laurent Simon,et al. Acoustic Emission Pattern Recognition Approach Based on Hilbert-Huang Transform for Structural Health Monitoring in Polymer-Composite Materials[J]. Applied Acoustic,2013,74:746-757.

[12] Li Lin,Fulei Chu. HHT-Based AE Characteristics of Natural Fatigue Cracks in Rotating Shafts[J]. Mechanical Systems and Signal Processing,2012,26:181-189.

[13] 张建伟,朱良欢,江琦,等. 基于HHT的高坝泄流结构工作模态参数辨识[J]. 振动、测试与诊断,2015,35(4):777-783.

蔡智超(1989-),男,讲师/博士后。主要从事工程电磁场、电磁无损检测、电工理论新技术等研究。参与国家自然科学基金3项,《IEEE Transactions on applied Supercon-ductivity》杂志评审专家,在电磁超声与声发射复合检测、换能器优化、非线性超声等方面发表SCI/EI收录十余篇,zccai@ecjtu.edu.cn。

PropagationCharacteristicsAnalysisofAcousticEmissionIntegratingElectromagneticUltrasonicCarrier*

CAIZhichao1*,ZHANGChuang2

(1.School of Electrical and Automation Engineering,East China Jiaotong University,Nanchang 330013,China; 2.Province-Ministry Joint Key Laboratory of Electromagnetic Field and Electrical Apparatus Reliability Hebei University of Technology,Tianjin 300130,China)

Electromagnetic acoustic emission technology(EMAE)does nondestructive detection with the effect of contactless electromagnetic loading to generate a stress field stimulating stress waves from the defective conductive structure. The most significant problem faced by the metallic structural health monitoring method of EMAE is that EMAE signal is not suitable for long distance transmission,this problem was improved by integrating electromagnetic ultrasonic carrier method. Firstly,based on free electron theory,the mechanism of EMAE was studied at a microscopic level which based on the activation energy changed from the electrical current to mobile dislocations. Secondly,the difference of stress wave propagation characteristics under various electromagnetic stimulating conditions was researched by building finite element model. Finally,the comparison between the energy percentage intrinsic mode functions of carrier experiment was discussed by Hilbert-Huang transformation. The stress wave propagation characteristics of EMAE was improved by integrating electromagnetic ultrasonic method which based on the study and improvement of traditional exciting,and the range of EMAE application will be widened.

electromagnetically induced acoustic emission;electromagnetic acoustic;integration;carrier;propagation characteristic

项目来源:国家自然科学基金青年项目(51307043);江西省青年科学基金项目(20171BAB216035)

2017-02-03修改日期:2017-04-19

TB553

:A

:1004-1699(2017)09-1335-08

10.3969/j.issn.1004-1699.2017.09.006