基于弹簧粒子模型的大规模WSN定位算法的衍生算法*

陈三风,韩 鑫,湛邵斌,胡 涛,卢 鑫,陈万明

(1.深圳信息职业技术学院信息技术研究所,广东 深圳 518029;2.江西理工大学机电工程学院,江西 赣州 341000；3.中国科学技术大学自动化系,合肥 230027)

基于弹簧粒子模型的大规模WSN定位算法的衍生算法*

陈三风1,2*,韩 鑫1,2,湛邵斌1,2,胡 涛1,2,卢 鑫1,2,陈万明3

(1.深圳信息职业技术学院信息技术研究所,广东 深圳 518029;2.江西理工大学机电工程学院,江西 赣州 341000；3.中国科学技术大学自动化系,合肥 230027)

为了提高基于弹簧粒子模型的大规模无线传感器网络定位算法(LASPM定位算法)的鲁棒性,将对LASPM基本定位算法进行优化及改进,并提出一系列的改进衍生算法。针对弱节点将设计简单的迭代定位方法,提出了3个补丁算法,分别用于处理局部极值、剔除坏节点和处理节点动态变化等问题。仿真实验结果表明,新算法的节点计算复杂度、通信复杂度在网络规模增大时仍然保持常量,节点计算步数不随网络规模变化而变化,时间复杂度也保持常量。实验研究结果表明,本文的定位算法具有良好的鲁棒性。

定位算法;弹簧粒子模型;大规模无线传感器网络;衍生算法;复杂度

为了扩大月球车的巡视和探测区域,需要建立一个包含数以万计无线传感器节点的大规模无线传感器网络。大规模无线传感器网络由大量的传感器节点构成,每个传感器节点的资源都受限,必须和其他传感器节点协同完成工作。目前,大部分无线传感器网络定位算法[1-4]的计算复杂度、通信复杂度和时间复杂度会随着网络规模的扩大而大大增加,这将导致大规模传感器网络系统瘫痪。针对以上问题,有关学者提出了基于质量-弹簧模型的定位算法[5-6],其要求网络中每个节点都具有测距能力,算法比较灵活,但是其计算复杂度比较高、收敛速度较慢、定位精度也不高。对此,本论文的研究者们提出了一种基于弹簧粒子网络模型的定位算法[7]LASPM(Localization Algorithm Based on a Spring Particle model)。LASPM定位算法模拟物理弹簧系统的动态变化过程,并借此计算出节点的位置坐标。该定位算法的计算复杂度比较,不会随着网络规模的扩大而增加,非常适用于大规模无线传感器网络。

近年来,相关研究者针对大规模无线传感器网络定位问题提出了一系列的分布式定位算法[8-11]。其中,APIT算法[8]要求锚节点密度较高,Euclidean算法[9],但其测量距离较为复杂。DV-Hop算法[10]适用于密集部署各向同性的大规模无线传感器网络。Robust positioning[11]算法的定位精度较高,但是计算复杂度非常高。MDS-MAP[12]算法需要集中式计算,以上定位算法均不适用于本论文的传感器网络。

鉴于月球车的传感器网络系统非常复杂,为了提高LASPM定位算法的鲁棒性,以适应月球的复杂环境,本论文将对LASPM定位算法进行改进优化并提出一系列的衍生算法。针对那些运算和存储功能较低的传感器网络节点,本论文将设计简单迭代定位方法。针对LASPM定位过程出现的BUG,本论文提出3个补丁算法,分别用于处理局部极值、剔除坏节点和处理节点动态变化等问题。

1 基于LASPM的简单迭代定位算法

根据文献[7]可知,LASPM定位算法模拟弹簧-粒子系统的运行状态过程,并计算出各个传感器节点的位置坐标。各传感器节点虚拟为具有质量的粒子,粒子间由弹簧相连。当外力将粒子放置到随机位置后,粒子间的弹簧将做相应的拉伸收缩运动。在弹簧力的作用下,粒子最终运动到它的初始平衡位置。整个过程中,模拟粒子运动的每个状态及相应的弹力,最终得到各节点的位置坐标。

各传感器节点定位每次迭代需接收众多相邻节点的虚拟坐标,计算该节点所受的合力、加速度、速度、位移等。然而,传感器网络中可能存在一些运算和存储功能较低的节点,对此,本论文将设计简单的迭代定位方法,使这些节点在每次迭代时无需计算节点受力合力、速度等,每次迭代时仅和一个邻节点交换虚拟坐标信息,然后根据节点间弹簧原长和现在弹簧长度的差异,这两个节点分别向它们连成的直线上相近或远离该弹簧伸长/收缩量的长度,使得这次迭代后,这两个节点间的距离等于它们原始距离。算法具体步骤如下:

首先 各节点通过各种测距方法[13](如RSSI等)获得邻节点间的初始一跳距离Ri,j;

然后 各节点向某个汇聚节点(Sink Node)发送以下信息:

Ii(IDi,is Anchor,{(IDj,Dij),(IDk,Dik),…})

该信息包含节点ID,是否为锚节点,到各个邻节点的一跳距离及相应邻节点ID;

最后 汇聚节点通过以下迭代算法求解计算该节点的位置坐标:

①未知位置节点位置初始化

首先求出所有锚节点的质心,然后确定最远锚节点到质心的长度,最后以该质心为圆心,该长度为半径作圆,使未知位置节点的坐标初始化于该圆之中。

②迭代收敛目标

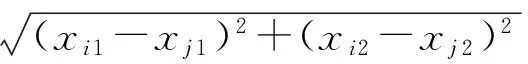
(1)

并使式(2)中的Err最小:

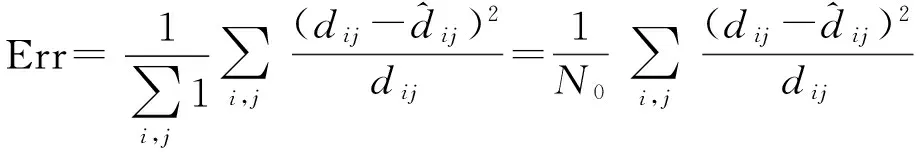
(2)

式(2)Err为所有相邻节点间平均一跳距离的绝对误差平方与相对误差平方的折衷,i,j为相邻节点。

③迭代过程

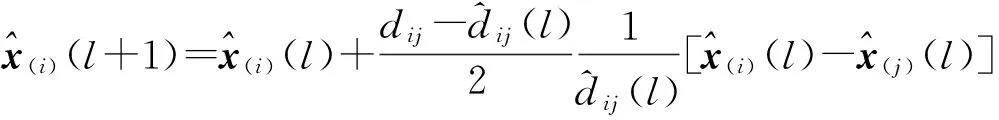
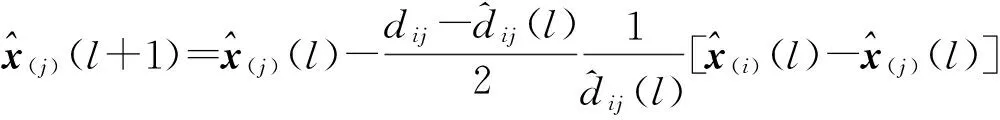
(3)

当l0次迭代结束后,其迭代增量为:

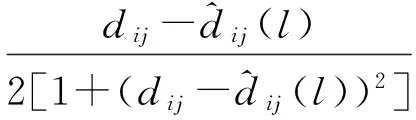
(4)

(b)当i,j中某个节点为锚节点时,假设

为i,其迭代过程如下:

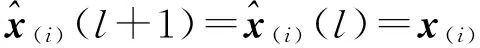
(5)

当l0次迭代结束后,其迭代增量为:

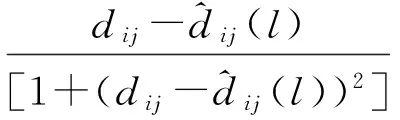
(6)

这将导致迭代步骤增加,但是降低了估计距离和测量距离仍然相差很大时的影响。经过一定的迭代次数后,多数节点间的估计距离和测量距离趋于一致,而仍然相差很大的那些节点可能因为测量距离与实际距离间误差很大,导致估计距离与测量距离无法一致。

2 基本LASPM定位算法的补丁算法(LASPM(P))

为了使LASPM能适用于不同的场合,提高其鲁棒性,本论文将在基本LASPM算法的基础上提出3个补丁算法(Patch)。当某些粒子没有稳定在它们的正确位置上时(如粒子为局部最优),使用Patch A来标志这些粒子,重新初始化它们的位置,并再次使用LASPM(B)(即基本LASPM定位算法),把它们拉到各自的正确位置上。当某些节点定位偏差很大(即为坏节点),使用Patch B标识它们,并给它们设置不同的置信度,并在后面使用定位信息时尽量选择置信度较高的节点,而抛弃或少用置信度低的节点。当网络中存在节点动态变化时,如有传感器节点加入或离开网络,使用Patch C标识这些节点。通过这3个补丁算法,使得LASPM算法在各种环境下会都具有良好的稳定性和鲁棒性。

2.1 Patch A(处理在不必要位置的粒子)

在有些特殊情况下,一些粒子稳定在不必要的位置。所谓不必要位置,即粒子所受邻居弹簧的合力为0,但是至少所受一个分力不为0;正确位置,即节点所受所有分力都为0时所处的位置。对于未稳定在正确位置的粒子,需对其进行处理。

每一个传感器节点都可以获取邻节点和它之间的距离,并把这些距离信息和弹簧的长度做比较,找出那些弹簧长度和距离信息不一致节点的,即不必要位置的粒子,然后把这些粒子从不必要位置处解救出来。

本论文采用以下两种方案进行修正。

①当发现这些粒子后,对它们的位置重新初始化,再次使用LASPM(B)算法将它们重新运行到新的位置,粒子可以稳定在它们的正确位置上。如果粒子运行到它的正确位置附近,它最终将稳定在它的正确位置上。

②因大部分节点都稳定在它们的正确位置上,可使用这些信息提高上述特殊粒子的位置精度。在二维系统中,若有3个及以上邻粒子稳定于它们正确位置上,采用极大似然法重新计算该粒子的位置坐标。

(7)

式中:(xi,yi)是需要求解的位置坐标,(xj,yj),(xk,yk),…,(xn,yn)是它的n个邻节点的坐标(n≥3),rij0,rik0,…rin0是它和邻节点间的距离。将式(7)线性化可得:

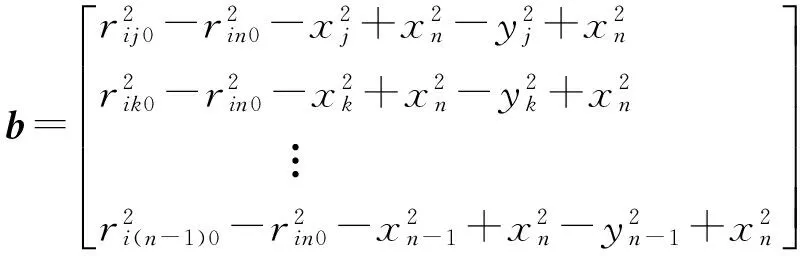
(8)

当计算出该粒子的坐标后,若这个位置坐标属于正确的位置,则通过式(10)可计算其他邻居节点位置。

如果没有粒子可用第2种方法来重新初始化位置,剩下的粒子仍用第1种方案重新初始化。当处于不必要位置的节点被重新初始化后,可以再次使用LASPM(B)算法,重新获取它们的位置。即使再次使用LASPM(B)后,仍然可能存在很少一部分节点,它们仍然没有运行到正确的虚拟位置上去,这时再次初始化,并再次使用LASPM(B)来减少这些特殊的节点。由实验得知,当再次使用LASPM(B)一次后,网络中所有节点的定位误差较小。

根据以上分析可知,Patch A算法是重新初始化某些节点的位置坐标,然后再次使用LASPM(B)算法,因此,LASPM(B)算法的某些性能仍然保持,比如计算复杂度、通信代价、收敛性以及最小误差平方和最优等。

2.2 Patch B(处理坏的节点粒子)

为了对月球探测器等目标进行更好的定位、跟踪和控制,必须将那些定位误差较大的节点挑选出来单独处理。在本论文中对每个节点的位置信息都设置一个置信度[0,1],数值越大表明置信度也越高,在实验中尽可能使用最高置信度节点的定位信息。本论文中,“定位误差较大”节点为:①该节点不能被定位;②节点被定位于不必要的位置上。

定理1在2维系统中,如果一个粒子与3个及以上不在一条直线上的其他粒子相连,那么这个粒子可以被定位。

证明如果2个粒子相连,那么这两个粒子之间的距离可以获得。当有3个粒子j,k,l知道它们的位置坐标以及它们和待定位粒子i的距离,采用以下三边函数计算粒子i的坐标(xi,yi):

(9)

本论文将研究一种快速且简单的方法来找出这些没有定位很好的节点,以供月球车的定位和导航等实验使用。本论文将用2种方法解决该问题,第1种算法较复杂,具体如下:

Step 1 选出互相连接的3个粒子,将它们放在一个集合内。使用这3个粒子,可以构建一个相对坐标系。

Step 2 如果有粒子和这个集合中至少3个粒子相连,那么这个粒子也可以被定位。所以将这个粒子也放入该集合中。这个集合中粒子的数目将会增加。

Step 3 如果有至少3个锚粒子在这个集合内,那么这个集合的所有粒子都可以通过坐标转换,进行绝对定位。

Step 4 没有被放在这个集合中的粒子在很大程度上不能被正确定位。

这个算法较复杂,并且未使用LASPM(B)的信息,须采用新的算法来寻找那些未成功定位的坏节点。

第2种算法如下:

Step 1 对于每个粒子,如果它处于不必要位置,将该粒子的置信度设置为0.5;如果它仅有1个或2个邻居粒子,则设置该粒子的置信度为0;其他粒子的置信度为1。

Step 2 对于每个粒子,如果它的置信度不等于1,则剪去和它相连的所有弹簧。它将不再是其他粒子的邻节点了。同时通知它以前的邻节点,从邻节点的表内删除自己。

Step 3 重复Step 1、Step 2,直到没有粒子可以需要更改它们的置信度。

传感器节点采用上述定位算法后,被分成了3类不同置信度的节点。在后续月球探测器定位和导航等应用节点坐标的场合时,尽可能使用更高置信度节点的定位信息。

2.3 Patch C(处理节点动态变化)

随着探月工程工作时间的增加、探测区域的增长,会有越来越多的节点加入或离开该无线传感器网络。在网络已成功定位后,须及时处理这些新变化的节点。

当一个新的盲节点加入网络中,它和它的邻节点进行通信,获取它们的位置和它们之间的距离。首先,将它的邻节点位置固定住;然后,新的节点使用LASPM[B]算法计算它的位置;最后,释放它的邻居节点,让这些邻节点使用LASPM算法做小的虚拟移动,以更新它们的位置坐标。当一个新的锚节点加入网络中,它和它的邻节点通信,告知它的位置坐标。这些邻节点可以使用LASPM算法,重新调整它们的位置坐标。

在某个节点正运行LASPM算法时,如有新节点加入,首先通过式(8)计算新节点大致位置,然后使用LASPM将该节点的位置信息广播给它邻居。邻节点收到该位置信息后,将该节点也加入到合力计算的成员中。

在LASPM算法完成后,如果有某个节点离开网络,若该网络是静止网络(传感器节点在部署后不再移动),其他节点的位置不须更新,即其他节点对该变化不做响应。如果网络是移动网络,其他节点将使用LASPM算法再次计算它们的位置。

在运行LASPM算法的过程中,如果有某个节点突然离开网络,它的邻居节点不会因为该节点的离开而陷入死锁。在LASPM算法过程中,每个传感器节点都设置有一个时间阈值。如果在时间阈值之后,它还没有收到所有邻居节点的位置信息,它将只使用目前收到的信息来计算它的位置、速度和加速度。因此,LASPM算法在节点快速加入或离开的动态网络中仍具有较好的适应性。

3 仿真实验

在本论文中,先验证简单迭代定位算法性能,然后深入对LASPM(B)和LASPM(P)算法进行性能验证评估,最后将LASPM算法与MDS-MAP算法进行比较。

3.1 简单迭代定位算法仿真实验

在规则的二维平面上,随机均匀分布200个节点,图1为该区域内的节点真实位置分布与通过本定位算法后估计出的位置分布。其中蓝色的圆圈所在处表示节点的真实位置,红线伸出去的末端为该节点的估计位置。

在图1中,本算法在节点间平均连接度为20,初始测距误差为5%,锚节点为20%时,本简单迭代定位算法的误差为5%。

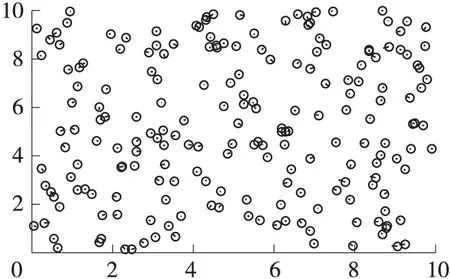
图1 简单迭代定位算法的节点定位分布图

3.2 LASPM(B)和LASPM(P)算法比较

本论文采用Matl对LASPM(B)和LASPM(P)算法进行比较仿真,仿真环境设置如下:在10r×10r的区域中,随机部署200个节点。r=1 是单位长度。如果距离误差是e,真实距离是d,那么测量距离满足正态分布d(1+N(0,e))。位置估计误差 err为R的倍数,R是节点的传输距离(也称为射频距离)。

式中:n是盲节点的数目,(xei,yei) 是节点i的估计位置,(xi,yi) 是该节点的真实位置。

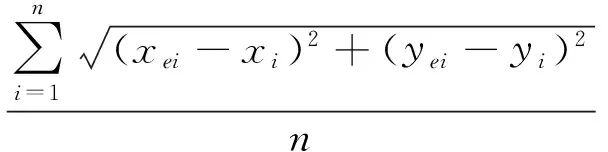
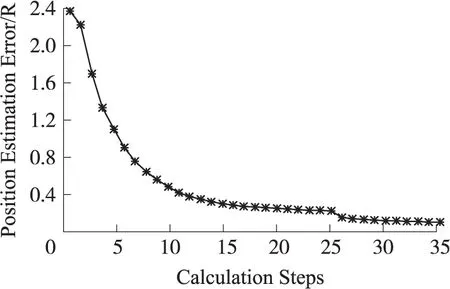
图2 LASPM算法定位过程(Tforce=1)

LASPM算法的仿真过程如图2所示,在该仿真实验中,网络中放置40个锚节点(占总节点的20%),射频距离R为1.5r,测距误差为5%。所有粒子的质量均相等,m=1,所有弹簧的弹性常量k=2,阻尼η=2,计算步数和合力的阈值分别为:lstep=700,Tforce=1,常量c=0.2。每个粒子的虚拟位置被随机初始化后,网络中初始的位置误差约为2.4R。然后,每个粒子在它们相连的弹簧的作用下,开始受到相应的拉力或压力。在弹力的作用下,粒子的虚拟位置开始变化很快。经过25个计算步数后,每个粒子所受的合力均小于Tforce,此时的定位误差是0.223 8。各个节点的估计位置和真实位置见图3,蓝色圆圈为盲节点的真实位置,红色圆圈为锚节点的真实位置,红线为节点的位置误差,线的两端分别为真实位置和估计位置。网络中大部分节点都已定位在真实位置附近,仅小部分节点(约20个)定位误差较大,这些节点被定位于不必要的位置上。

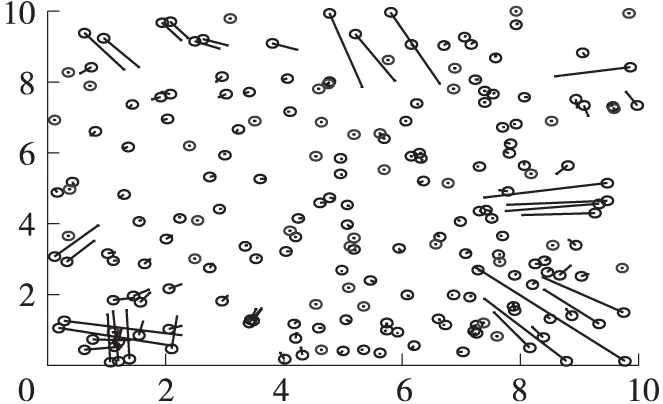
图3 LASPM[B]算法定位结果(Tforce=1)

将这些不必要位置的节点重新初始化位置坐标,并再使用LASPM(B)一次,即使用Patch A算法,网络中节点的定位误差下降到0.101 4。各个节点的估计位置和真实位置见图4。其将大部分处于不必要位置上。的节点定位在正确位置上。若再重新初始化,定位误差将更小。

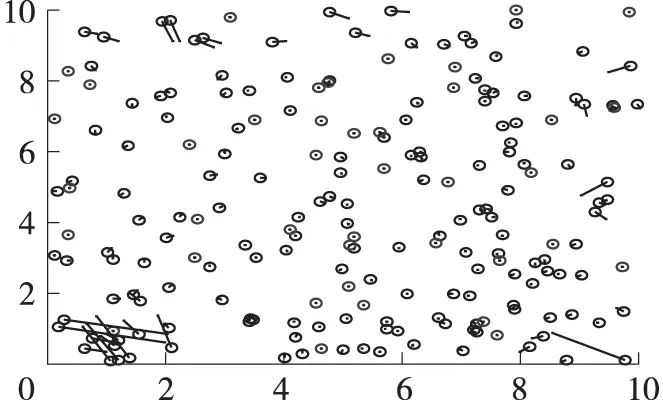
图4 LASPM[P]算法定位结果(Tforce=1)

3.3LASPM算法的鲁棒性论证

为了验证LASPM算法的抗干扰性,即鲁棒性,进行了仿真实验验证。在该实验中随机产生100 个粒子,在每个粒子中,所有节点的真实位置和虚拟位置都是随机部署于既定的网络区域内,各相邻节点间的测量距离也随机设置(测量误差),其他参数与图3中设置一致。

图5、图6分别为LASPM(B)和LASPM(P)的计算步数。在LASPM(B)算法中,粒子的 计算步数均小于300,平均计算步数小于100。即网络节点的计算步数比较稳定,它不会随着初始化而剧烈变化。在LASPM(P)算法中,平均计算步数为160步,即重新初始化后,再次使用LASPM(B)后的平均计算步数为160-100=60,算法的收敛速度更快。图7、图8分别为LASPM(B)和LASPM(P)的定位误差。在LASPM(B)算法中,最大定位误差为0.5,平均定位误差为0.2。在LASPM(P)算法中,平均定位误差小于0.1,LASPM(P)算法的定位精度更高。

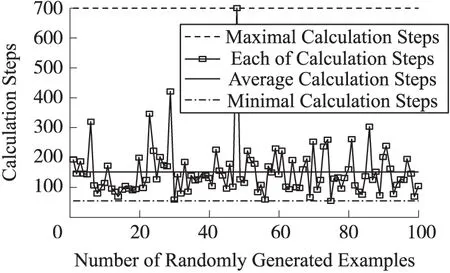
图5 LASPM(B)的计算步数

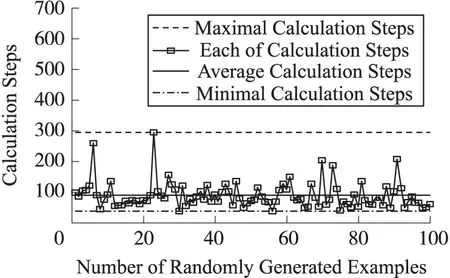
图6 LASPM(P)的计算步数

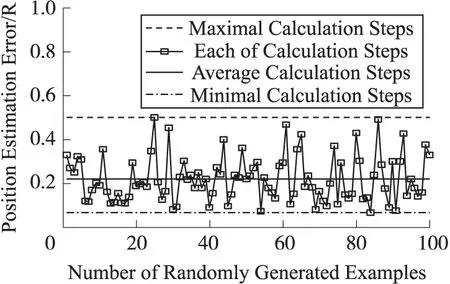
图7 LASPM(B)的定位误差

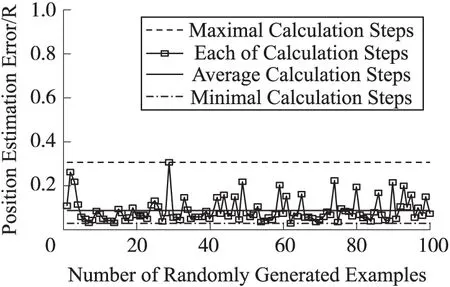
图8 LASPM(P)的定位误差

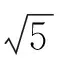
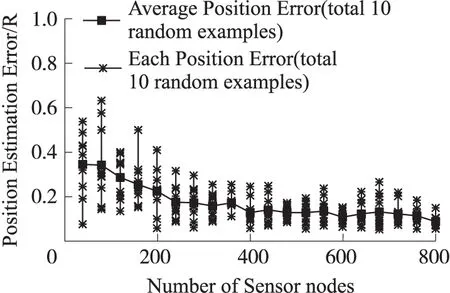
图9 LASPM(B)的定位误差V.S.节点数

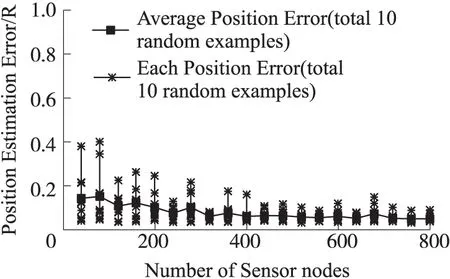
图10 LASPM(P)的定位误差V.S.节点数

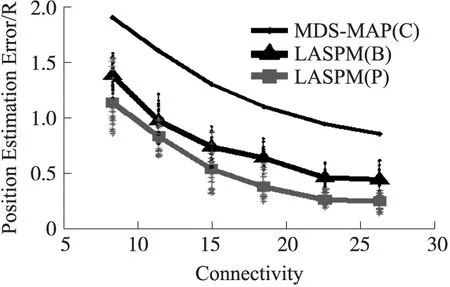
图11 规则网络的定位误差

4 LASPM和MDS-MAP的比较

为了进一步验证LASPM定位算法性能,本论文将其与经典的分布式定位算法MDS-MAP进行仿真比较。首先,在规则网络中进行实验仿真比较。网络中总节点数200,锚节点数10,部署区域为10r×10r的2维区域[1]。射频距离R从1.25增加到2.5,每次增加0.25。随机部署节点,传感器网络定位误差对比如图11所示。当连通度较小时,LASPM算法的定位精度比MDS-MAP低。当连通度较大时,两者精度类似。

另外,在C形网络中进行实验比较。在该实验中,网络节点数160,锚节点数10,部署区域为10r×10r的2维C形状区域[1]。射频距离R从1.25增加到2.5,每次增加0.25。相对应的连通度分别为8.197 5,11.293 1,14.640 6,18.856 2,22.113 8和27.627 5。随机部署节点,LASPM算法的定位精度和MDS-MAP(P)的相似。从图12可发现当连通度从小变大时,LASPM法的定位精度一直较MDS-MAP(C)的高。这是因为MDS-MAP(C)算法中两个距离参数相差巨大,其导致MDS-MAP(C)算法在不规则区域内定位精度较低。本论文算法只使用节点间一跳距离,因而定位精度较高。

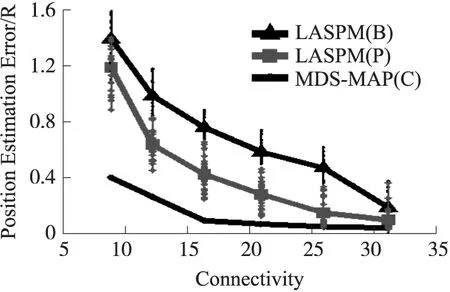
图12 C形网络的定位误差

这两个算法的相关性能参数如表1所示,LASPM算法的计算复杂度、通信复杂度均比MDS-MAP(C)小。因此,LASPM算法非常适合于大规模无线传感器网络中。

表1 LASPM与MDS-MAP算法比较

5 结论

本论文为基于弹簧粒子模型的LASPM算法的衍生和改进。针对适应运算存储能力更低的无线传感器网络节点,本论文提出了源于LASPM定位思想的简单迭代算法;为了处理不同无线传感器网络定位过程的不同情况,本论文提出了基于LASPM(B)的3个补丁算法,用来处理节点定位过程中陷入局部极值,处理坏节点和处理无线传感器网络节点动态加入离开的问题,并仿真实验验证这些衍生算法是可行。

[1] 张会新,陈德沅,彭晴晴,等. 一种改进的TDOA无线传感器网络节点定位算法[J]. 传感技术学报,2015,28(3):412-415.[2] Shang Y,Ruml W,Zhang Y,et al. Localization from Connectivity in Sensor Networks[J]. IEEE Transactions on Parallel and Distributed Systems,2004,15(11):961-974.

[3] Wang Y,Wang X,Wang D,et al. Range-Free Localization Using Expected Hop Progress in Wireless Sensor Networks[J]. IEEE Transactions on Parallel and Distributed Systems,2009,20(10):1540-1552.

[4] Kulkarni R V,Forster A,Venayagamoorthy G K. Computational Intelligence in Wireless Sensor Networksy[J]. IEEE Journal Communications Surveys and Tutorials,2011,13(1):68-96.

[5] Pandey S,Prasad P,Sinha P,et.al. Localization of Sensor Networks Considering Energy Accuracy Tradeoffs[C]//International Conference on Collaborative Computing:Networking,2005:1-10.

[6] 杨友华,孙丽华,向满天. 基于质点弹簧模型的无线传感器网络非测距定位算法[J]. 传感技术学报,2015(6):914-919.

[7] 陈三风,梁永生,陈万明,等. 基于弹簧粒子模型的大规模WSN定位算法研究[J]. 小型微型计算机系统,2012,33(8):1697-1700.

[8] 吴凡,彭力,董国勇. WSN中基于中位线分割的APIT定位算法[J]. 小型微型计算机系统,2015,l36(7):1583-1586.

[9] Nguyen V H,Berder O,Langlais C. Distributed Minimum Euclidean Distance Based Precoding for Wireless Sensor Network[C]//International Conference on Computing,Networking and Communi-cations,2015:918-923.

[10] 张震,闫连山,刘江涛,等. 基于DV-Hop的无线传感器网络定位算法研究[J]. 传感技术学报,2011,24(10):1470-1472.

[11] Savarese C,Rabaey J M,Langendoen K. Robust Positioning Algorithm for Distributed Ad-Hoc Wireless Sensor Networks[C]//Proc of the General Track of the Annual Conference on USENIX Annual Technical Conference,Berkeley,CA,USA,2002:317-327.

[12] 马震,刘云,沈波. 分布式无线传感器网络定位算法MDS-MAP[J]. 通信学报,2008,29(6):57-63.

[13] 杨文铂,邢鹏康,刘彦华. 一种基于自适应RSSI测距模型的无线传感器网络定位方法[J]. 传感技术学报,2015,28(1):137-141.

陈三风(1979-),女,博士,,副教授,硕士生导师,主要研究方向为无线传感器网络,机器人学等,chensanf@sziit.edu.cn;

卢鑫(1975-),男,工学博士,教授,主要研究领域为通信技术,物联网等。

DerivativeLocalizationAlgorithmsBasedonaSpringParticleModel(LASPM)forLargeScaleWirelessSensorNetworks*

CHENSanfeng1,2*,HANXin1,2,ZHANShaobin1,2,HUTao1,2,LUXin1,2,CHENWanming3

(1.Institute of Information Technology,Shenzhen Institute of Information Technology,Shenzhen Guangdong 518029,China; 2.School of Mechanical and Electrical Engineering,Jiangxi University of Science and Technology,Ganzhou Jiangxi 341000,China; 3.Department of Automation,University of Science and Technology of China,Hefei 230027,China)

To improve the robustness of localization algorithm based on a spring particle model(LASPM)for large-scale wireless sensor networks,some derivative algorithms based on basic LASPM algorithm are proposed. A simpler iterative algorithm is proposed for weak particles. Three patches of the basic LASPM algorithm are proposed to avoid local optimization,kick out bad nodes and deal with node variation. Simulation results show that the computational and communication complexity are almost constant despite the increase of the scale of the network. The time consumption has also been proven to remain almost constant since the calculation steps unrelated to the scale of the network. The proposed localization algorithms are shown with sound robustness.

localization algorithm;spring particle model;large scale wireless sensor networks;derivative algorithms;complexity

项目来源:广东省自然科学基金项目(2015A030313587;深圳市科技计划项目(JCY20160307100530069,GRCK20160415111850716)

2017-01-25修改日期:2017-05-12

TP393

:A

:1004-1699(2017)09-1405-07

10.3969/j.issn.1004-1699.2017.09.018