基于分布式梯度算法的WSN隐私保护技术研究*
2017-09-22王军号
王军号,黄 娟,杜 朋
(安徽理工大学计算机科学与工程学院,安徽 淮南 232001)
基于分布式梯度算法的WSN隐私保护技术研究*
王军号*,黄 娟,杜 朋
(安徽理工大学计算机科学与工程学院,安徽 淮南 232001)
数据隐私保护技术是WSN领域的研究热点之一,针对数据隐私保护问题提出了一种基于分布式梯度算法的密钥管理策略。把网络拓扑结构抽象为有向图,每个节点都有各自的目标函数,密钥采用异步更新方式。更新过程中,每个节点的梯度值由目标函数给出,通过分布式优化算法求得全局目标函数的最优解,以此来计算通信密钥。随机因子依据数据与梯度的差值自适应调整作动态变化,攻击者无法获取随机因子及相关参数,从而达到隐私保护的目的。论文从隐密性、收敛性、有效性3个方面验证分析了该算法的优越性。
无线传感器网络;隐私保护;分布式梯度算法;密钥管理策略
在无线传感器网络中,隐私保护已经成为研究的热点之一。无线传感器网络WSN(Wireless Sensor Networks)是由许多传感器节点组成,一般部署在无人看守的恶劣环境下,它具有感知监测、采集数据以及计算处理能力。在实际应用中面临着数据泄露或者被攻击的威胁,攻击者可以通过对数据窃听、伪造或者非法授权传感器节点等一系列方法获取数据信息,这严重影响了WSN的未来发展。因此,研究和解决WSN数据隐私保护问题,对传感器网络的广泛应用具有非常重大的意义[1]。目前,密钥管理策略的研究成果主要集中在节点安全、更新高效、抗节点俘获攻击和复制攻击等方面。针对无线传感器网络的隐私保护问题,本文提出了一种基于分布式梯度算法的密钥管理策略,该策略能够提高网络的隐私性、收敛性和有效性,从而提高网络安全性,降低网络通信开销,延长网络寿命。
文献[2]针对WSN数据隐私保护现有的研究成果进行了总结,提出了一种基于身份加密的传感器网络密钥分配方案,该方案的抗毁性较强,但是额外的开销比较大。文献[3]介绍了分布式次梯度同步优化算法,但该算法的隐私保护性能较弱。本文设计了一种基于分布式梯度算法的密钥管理策略,该算法中,每个节点独立构造目标函数,密钥采用异步更新方式,并由全局目标函数计算最优解而得到,随机因子自适应动态调整,从而使得攻击者无法获取随机因子及相关参数,避免了恶意攻击者的破坏或信息泄露,达到隐私保护的目的。
1 分布式梯度算法的WSN密钥管理策略
本文是对WSN传感器节点数据进行保护的,以防恶意节点破坏。文中使用分布式梯度算法的密钥管理策略,以至于提高了数据隐私保护的性能。
1.1 分布式梯度算法
论文采用分布式梯度算法来进行数据隐私保护,梯度算法被广泛应用在数学、信息处理及隐私保护等领域,在计算机领域中的机器学习和神经网络中的应用较为广泛[4]。
文献[5]中介绍了梯度算法出现在上世纪80年代,最近几年得到了快速发展,在大数据和云计算环境下,成为分布式无线传感器网络中求函数极值的方法之一。梯度算法中对每个节点数据进行独立异步更新,构造目标函数:
(1)
式中,函数fj:Rm→R是节点j的目标函数,n为节点个数;在分布式梯度算法中,每个节点仅仅知道自己的目标函数。
在网络部署中,每个传感器节点设定时间分片,每个时间分片内节点采集和更新数据,对于分布式梯度算法隐私保护是一个迭代过程,经过有限次更新,最终获得最优解[6],具体迭代公式如下:
Hk+1=Hk+OkRk
(2)
Ok=fk(x)-Tk-1
(3)
式中:Hk+1表示更新后的数据,Tk-1是节点前一次采集的数据;Ok是随机因子,动态变化的,主要是依据个体获得数据与梯度的差对该参数进行自适应调整,Ok的选取至关重要;每个节点获得一个初始估计数据,表示为Hk;Rk表示更新数据时目标函数的查找方向一般选取负梯度方向(也可选择正梯度方向):
(4)
式中:ηk为常数且ηk∈(0,1)。
1.2 分布式梯度算法密钥管理方案
为了建立分布式梯度算法,把无线传感器网络拓扑结构抽象为有向图,节点作为有向图的顶点,数据交互信息作为边,如图1所示。
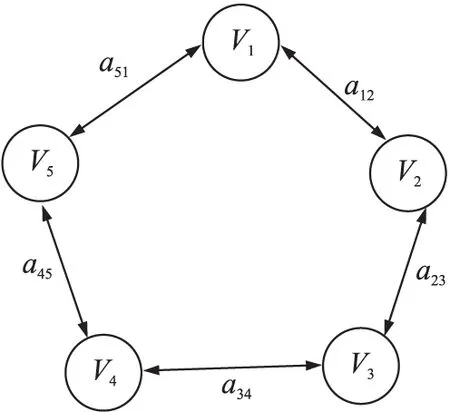
图1 WSN网络抽象图
把网络抽象为一个有向图G(V、E、A),V是顶点(每个节点个体),E是传感器节点交互信息的边,A表示邻接矩阵,邻接矩阵[A]ij是表示从顶点Vi到Vj传输数据的值,记为权重a[ij];针对分布式梯度算法的密钥管理策略,本文提出3个基本的假设[7]:
①图G是连通的,fi是光滑的凸函数;

③fi的梯度是有界的,例如:若M>0,存在d∈fk(x),使得‖d‖≤M,∀x∈Rm。
而邻接矩阵[A]ij表示如下:
(5)
通过目标函数公式(1)和邻接矩阵公式(5)对节点采集的数据a[ij]进行处理,得到最优梯度值。具体如下式:
(6)
为了使式(1)达到最优解,结合上述公式,设计了一种分布式梯度优化方法:

(7)
式中:节点j在t时刻式(1)的最优解是xk(t),fk(t)表示函数fk梯度,节点j在t=0时刻的初始梯度值为fk(0)。通过分布式梯度优化方法,求得全局目标函数的最优解,即为节点j与连接节点i的通信密钥[8]。
本文设计的分布式密钥管理算法,不仅可以使个体之间的数据得到有效的保护,而且算法采用的异步更新机制能够确保采集的数据在迭代过程中不被攻击者破解,有利于通信密钥的安全。综上所述,论文基本思想是:利用分布式梯度优化式(7)对目标函数(1)求其最优解,求得的最优解就是本文需要保护的对象,恶意节点无法获得最优解就无法获得密钥信息;随机因子的选取对迭代方法至关重要,它是由前一次采集的数据与每次得到的梯度求差为依据自适应调整;在数据更新过程中,参数动态变化,恶意节点无法获取真实数据,达到了隐私保护的目的。该算法的流程如图2所示。
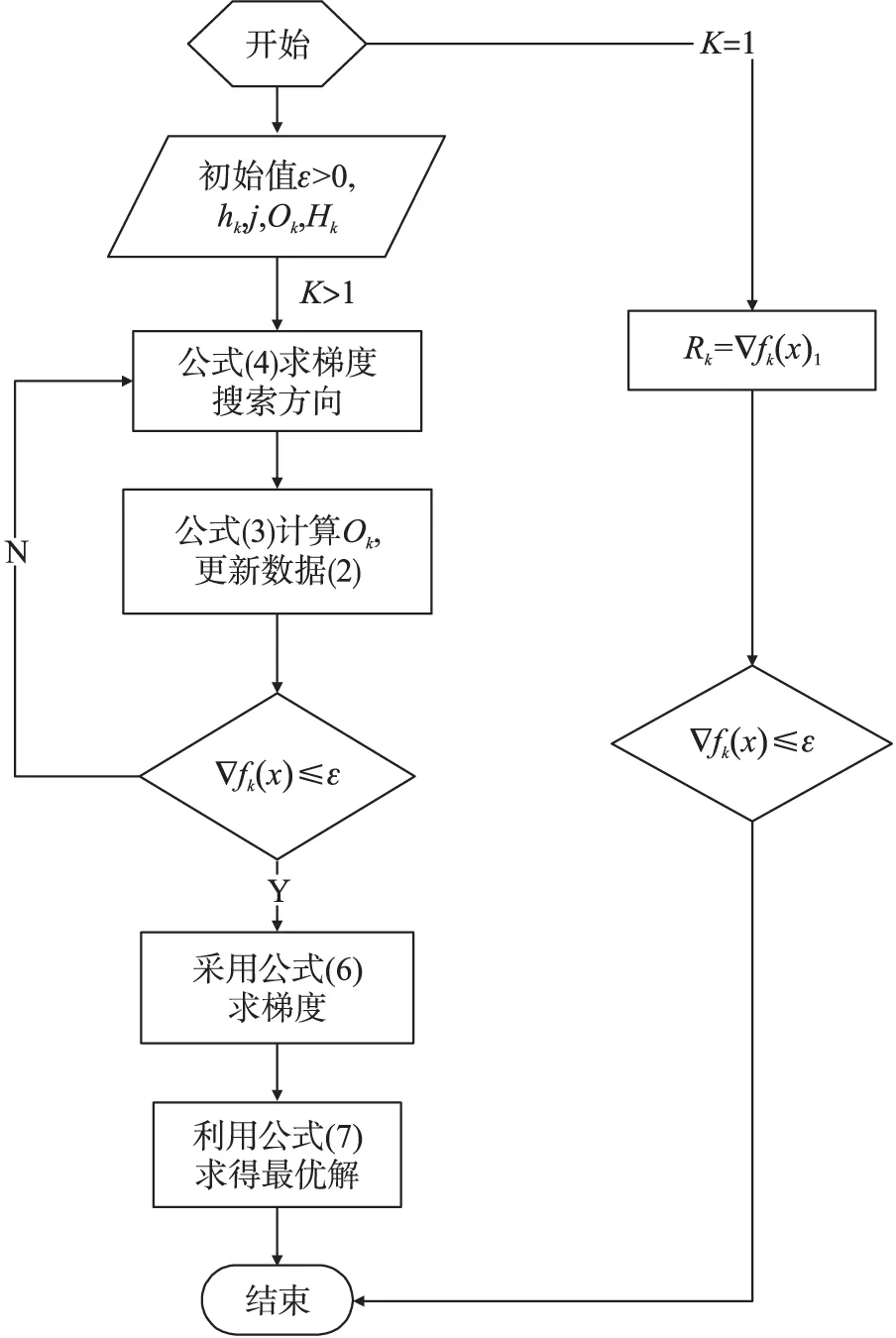
图2 算法流程图
1.3 具体实现
分布式梯度算法对数据隐私保护是通过对目标函数(1)求其最优解,获得通信密钥。具体实现步骤如下:
Step 1 给定初始值ηk,x1∈Rn,ε>0,Rk=-f(x)1,若f(x)1≤ε,则停止;当ε≤0时,利用式(4)计算负梯度搜索方向;
Step 2 由式(3)计算随机因子Ok数值;
Step 3 传感器节点采集的数据用式(2)进行更新,数据更新结果存储在矩阵中;
Step 4 使用式(1)、式((6)求节点的目标函数及最佳梯度值;
Step 5 采用分布式梯度优化算法式(7)计算全局目标函数的最优解,获得通信密钥;
Step 6 重复上述步骤.
伪代码如下:
program WSN;
varηk,Ok,Hk,ε:real;
begin
read ln(ηk,Ok,Hk,ε);
forj:=1 tondo //循环变量对n个个体
begin
Hk+1∶=Hk+okRk; //更新数据
Ok=fk(x)-Tk-1; //计算随机因子
Rk=-f(x)k+ηkRk-1; //梯度搜索方向
终止计算;
end;
forj:=1 ton
write ln[xk(t)]; //得到通信密钥
end
2 性能分析
下面分别从隐密性、收敛性、有效性3个方面分析验证该算法对WSN数据隐私保护的性能。
2.1 隐密性
由于本文的通信密钥采用分布式梯度算法动态异步更新机制,由第2部分的算法公式可知,密钥更新过程中,在每个节点的目标函数构造的a[ij]矩阵里,随机因子Ok由前一次采集的数据与每次得到的梯度求差,把传输数据作为权重保存在邻接矩阵中,任何m 从图3可以看出,本文所采用的算法隐私性要优于文献[10]中的方案,且随着网络规模的变化,隐私保护性能逐渐变低。当η<0.01(η∈ηk,即η∈(0,1))时,本文方案中节点连接被暴露的概率远低于1%,在很大程度上满足了隐私保护需求。 图3 隐密性对比图 2.2 收敛性 本文采用的分布式梯度算法利用迭代回归更新数据之后再求梯度值,把传输数据作为权重保存在邻接矩阵中,每个节点的梯度值由目标函数给出,通过分布式优化算法求得全局目标函数的最优解,经过500步计算,收敛于规定的精度要求,获得最优解。对本文算法和文献[11]中的E-G算法的收敛速度进行比较,通过实验仿真,得到收敛效果如图4所示。 图4 收敛效果 可以看出分布式梯度算法收敛曲线经过500步就达到了规定的精度要求,远远高于E-G算法的收敛速度。可见与E-G算法相比,本文设计的保护数据隐私分布式梯度算法相对合理,使得它的收敛速度明显加快,即需用较少的时间和步数,就能达到满足误差精度的要求。因此,分布式梯度算法的收敛效率更高。 2.3 有效性 有效性主要指计算开销和通信开销,通过2.2节中收敛性的分析可以看出,在计算开销上,由于本文的密钥分配算法的收敛性较优于E-G算法,因此其计算开销要小于E-G算法。由于计算开销所占比重相对较少,所以重点对算法的通信开销进行分析研究。在通信开销上,该算法采用了新的密钥分配系统和异步更新机制,既可以有效地剔除了无用节点,避免了无用节点的运算和通信,又可以减少通信堵塞,降低通信量[12]。通信量是由节点发送数据包的数量来衡量的,图5给出了在不同簇大小的情况下,两种方案簇内传输数据包的情况,可见本文方案的通信开销要低于E-G算法,且额外开销非常有限。 图5 通信量对比图 通过仿真实验可得,随着信息长度的增加,分布式梯度算法的精确度逐渐提高,改善了隐私保护的性能,使得敏感数据能够得到更有效的保护,因此,本文提出的基于分布式梯度算法在无线传感网数据隐私保护中更具有实用价值。 本文提出了一种基于分布式梯度算法的密钥管理策略,算法中每个节点都有各自的目标函数,采用异步方式更新数据,动态的随机因子依据数据与梯度的差值自适应调整,而每个节点的梯度值由目标函数给出,通过该方法求得全局目标函数的最优解,从而设计了一种分布式梯度的密钥算法,攻击者无法获取随机因子及相关参数,因此避免了恶意攻击者的破坏或信息泄露,达到了隐私保护的目的。论文从隐密性、收敛性、有效性3个方面分析验证了该算法的性能,证明该算法在上述3个方面具有一定的优越性,能够实现WSN隐私保护的功能。 [1] 张江南,褚春亮. 无线传感器网络中源节点位置隐私保护方案研究[J]. 传感技术学报,2016,29(9):1405-1409. [2] Bechkit W,Challal Y,Bouabdallah A,et al. A Highly Scalable Key Pre-Distribution Scheme for Wireless Sensor Networks[J]. IEEE Transactions on Wireless Communications,2014,12(2):948-959. [3] Lou Y,Yu L,Wang S. Privacy Preservation in Distributed Subgradient Optimization Algorithms[J]. Computer Networks,2016,38(4):393-422. [4] Lobel I,Ozdaglar A. Distributed Subgradient Methods for Convex Optimization Over Random Networks.[J]. Automatic Control IEEE Transactions on2010,56(6):1291-1306. [5] Jakovetic D,Bajovic D,Krejic N,et al. Distributed Gradient Methods with Variable Number of Working Nodes[J]. Mathematics,2016,64(15):761-773. [6] Neglia G,Reina G,Alouf S. Distributed Gradient Optimization for Epidemic Routing:A Preliminary Evaluation[C]//IFIP Conference on Wireless Days,2009:288-293. [7] Han S,Ng W K,Wan L,et al. Privacy-Preserving Gradient-Descent Methods[J]. IEEE Transactions on Knowledge and Data Engineering,2009,22(6):884-899. [8] Wan L,Ng W K,Han S,et al. Privacy-Preservation for Gradient Descent Methods[C]//ACM SIGKDD International Conference on Knowledge Discovery and Data Mining,2007:775-783. [9] Jakovetic A,Moura J M F,Xavier J. Distributed Nesterov-Like Gradient Algorithms[J]. Mathematical and Computer Modelling,2012,23(1):5459-5464. [10] Sun Y,Speranzon A,Mehta P G. A Key-Management Scheme for Distributed Sensor Networks[J]. IEEE Transactions on Signal Processing,2016,64(15):362-375. [11] Duchi J C,Agarwal A,Wainwright M J. Dual Averaging for Distributed Optimization:Convergence Analysis and Network Scaling[J]. IEEE Transactions on Automatic Control,2015,57(3):592-606. [12] Tsianos K I,Rabbat M G. Distributed Dual Averaging for Convex Optimization under Communication Delays[C]//American Control Conference,2012:1067-1072. 王军号(1970-),男,江苏赣榆人,硕士生导师,研究方向为信号与信息处理,计算机网络与通信。 ResearchonPrivacyPreservingTechnologyBasedonDistributedGradientAlgorithminWSN* WANGJunhao*,HUANGJuan,DUPeng (School of Computer Science and Engineering,Anhui University of Science and Technology,Huainan Anhui 232001,China) Data privacy protection technology was one of the research hotspot issues in the field of WSN. This paper proposed a key management strategy based on distributed gradient algorithm for data privacy protection. The network topology was abstracted as a directed graph,in which each node had its own objective function,and the private key was updated in an asynchronous way. In the process of updating,the gradient value of each node was given by the objective function. And the communication key could be calculated this way in which the optimal solution of the global objective function was obtained through the distributed optimization algorithm. The purpose of privacy protection was achieved because the random factors could be adjusted dynamically according to the difference between the data and the gradient so that the attacker cannot receive random factors and relevant parameters. The superiority of the proposed algorithm in this paper is verified by three aspects:privacy,convergence and validity. WSN;privacy protection;distributed gradient algorithm;private key management strategy 项目来源:国家自然科学基金项目(61300001);安徽省质量工程教学研究项目(2016jyxm0266) 2017-03-09修改日期:2017-04-26 TP393 :A :1004-1699(2017)09-1396-05 10.3969/j.issn.1004-1699.2017.09.016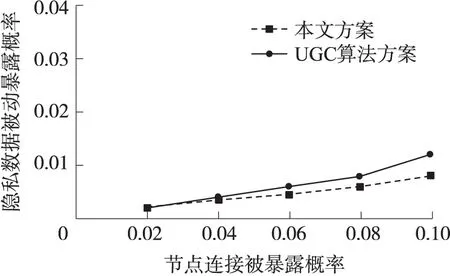


3 结论

