联合TDOA-AOA无线传感器网络半定规划定位算法研究*
2017-09-22张文华于洁潇刘开华
张文华,于洁潇*,刘开华,赵 宇
(1.天津大学电气自动化与信息工程学院,天津 300072;2.天津大学微电子学院,天津 300072)
联合TDOA-AOA无线传感器网络半定规划定位算法研究*
张文华1,于洁潇1*,刘开华2,赵 宇1
(1.天津大学电气自动化与信息工程学院,天津 300072;2.天津大学微电子学院,天津 300072)
在无线传感器网络定位中,TDOA和AOA联合定位可有效利用多种位置信息提高定位精度。由于传统联合加权最小二乘(WLS)的目标函数非线性,在应用于无线传感器网络定位时,会产生多个局部最优解。因此,针对该问题本文将约束加权最小二乘问题转化为二次约束二次规划问题,之后通过引入半定松弛(SDR)方法将联合定位问题转换为低复杂度的半定规划问题(SDP),进而寻找全局最优解。并且针对实际应用中参考节点带误差的情形分析和推导了定位算法。与已有算法相比,提出的算法在参考节点无误差和有误差时都有更高的精度。此外,提出的SDP算法还能够实现只有两个参考节点下的目标定位。
无线传感器网络;目标定位;到达时间差;到达角度;半定规划
由于无线传感器网络(WSNs)在无线通信,室内定位和水声传感器网络(UASN)[1]等领域的重要应用,精确的无线传感器网络定位算法近年来受到了广泛的关注。针对接收信号的不同特征参数,基于测距的定位方法主要有RSS(Received Signal Strength)[2],TOA(Time Of Arrival)[3],TDOA(Time Difference Of Arrival)[4]和AOA(Angle Of Arrival)[5-6]4种方法。对于不同的定位场景和精度要求可以选择相应的定位算法。然而,在非视距(NLOS)或参考节点有限的复杂环境下,使用上述算法之一与精确定位的要求相去甚远。因此,联合定位算法的研究逐渐受到重视。
为了提高复杂环境下的定位精度,相应的联合定位算法有TOA-AOA[7]、AOA-RSS[8]以及TDOA-AOA。在上述算法中,相对于TDOA-AOA,TOA-AOA算法需要高精度的时间同步,而AOA-RSS易受到衰落效应的影响[9]。本文研究TDOA-AOA联合定位算法。为了提高TDOA-AOA联合定位的精度,Li等[10]提出了二维空间中联合TDOA-AOA两步加权最小二乘(Two-Step LS)定位算法,其算法精度高于单独使用TDOA的定位精度。Cheung等[11]通过使用联合TDOA-AOA约束加权最小二乘法(CWLS)定位移动基站,但是当参考基站少于4个时其定位性能急剧下降甚至算法失效。Yin等[12]提出了两基站下基于TDOA-AOA的定位闭式解,然而,该方法只能用于三维空间的定位,且受限于权矩阵的秩和条件数,其定位鲁棒特性较差。上述算法都只是局部优化算法,并不能保证找到全局最优解。
由于目标位置与测量值之间的非线性和非凸性关系,无线传感器网络定位问题的求解较为复杂。而用于求解定位的最小二乘(LS)和最大似然(ML)估计方法并不能保证获得全局最优解。凸优化(Convex Optimization)是数学最优化的一个子领域,研究定义于凸集中的凸函数最小化的问题,能用于寻找全局最优解。因此,可以通过引入凸松弛(SDR)方法,将NLS或ML问题松弛为等效的半定规划(SDP)问题,进而获取全局最优解。近年来,SDP算法开始用于基于测距的定位问题中[13]。但是在TDOA-AOA联合定位算法中还缺乏探索。
本文通过研究二维空间的联合TDOA-AOA加权最小二乘算法,提出一种新的基于半定规划(SDP)的凸优化算法。第2节建立了定位场景,并推导了联合WLS算法;第3节将其转化为等效的二次规划问题,之后通过引入冗余变量和SDR技术将二次规划问题转换成SDP凸优化问题。第4节对参考节点带误差的定位进行了推导,并提出了相应的凸优化算法。通过第5节的仿真结果可以证明本文SDP定位算法的优越性。
1 定位场景及加权最小二乘算法
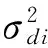
1.1TDOA分析
不失一般性的,将第1个节点作为到达时间差的参考节点,其他节点测量的相应距离差可以表示为:

(1)
式中:ndi表示测量噪声。则真实距离差可以表示为:
(2)
而测量所得的时间差可以表示为:
(3)
式中:c为信号传播速度。为了简化公式,全文使用式(1)中的距离差进行推导。
不考虑测量误差,(1)中的ri可以表示为:
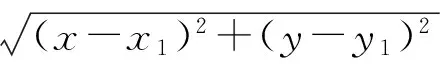
(4)
式(4)两边平方并作等价代换x-xi=(x-x1)-(xi-x1),可以得到
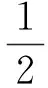
(5)
1.2AOA分析
角度测量值可以表示为式(6):
(6)
式中:nθi为测量噪声,相应的真实测量角度为:
(7)
不考虑测量噪声,(6)可表示为:
xsinθi-ycosθi=xisinθi-yicosθi
(8)
两端同时加y1cosθi-x1sinθi可得[11]
(x-x1)sinθi-(y-y1)cosθi=(xi-x1)sinθi-(yi-y1)cosθi
(9)
1.3 联合TDOA-AOA加权最小二乘法
考虑带测量噪声的全部TDOA和AOA测量值,可以得到[11]
Gdz=hd-ed
(10)
Gθz=hθ-eθ
(11)
式中
(12)
(13)
(14)
(15)
(16)
通过将式(2)、式(7)分别代入式(10)、式(11),忽略噪声二次项,可以分别得到edi≈dindi和eθi=disinnθi≈dinθi。
将式(10)和式(11)合并可得
Gz=h-e
(17)
式中:G=[GdGθ]T,h=[hdhθ]T,e=[edeθ]T。此时未知节点的坐标可以由加权最小二乘求解:
z=(GTW-1G)-1GTW-1h
(18)
而:
W=E[eeT]=BQBT
(19)
(20)
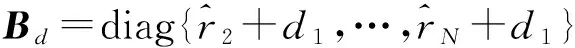
Q为噪声的协方差矩阵。
在实际定位中,式(18)中的权矩阵W未知,其具体数值需要由未知节点的真实位置确定。在这里我们可以先使用单位矩阵代替W进行初始位置估计,之后使用初始化的位置信息通过(19)计算权矩阵。仿真结果显示一次迭代就能实现定位,多次迭代并不会有实质性提升。
2 参考节点无误差时的半定规划(SDP)定位算法2.1 WLS算法的重构
式(18)的加权最小二乘估计可以等效地写为:
(21)
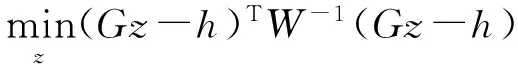
(22)
在对(22)中的目标函数和约束条件即2范数进行分解后,可以得到一个二次约束二次规划问题:
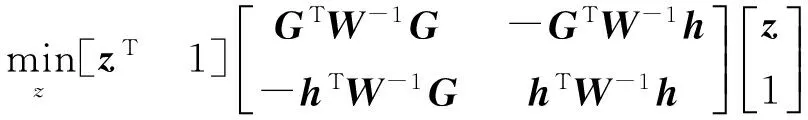
(23)
式中:Σ=diag(1,1,-1,0)。
2.2 联合定位的半定规划(SDP)算法
式(23)中:目标函数和约束条件都是非线性的,这里可以通过引入冗余变量Z=zzT,其中
(24)
使用基本性质xTAx=tr{xxTA},式(23)可以被等效为新的约束优化问题:

(25)
Z=zzT
(26)
式(26)的约束条件非凸,可以使用半定松弛(SDR)技术,即等效为两个条件:rank(Z)=1和Z为对称半正定(PSD)矩阵,通过松弛秩约束,可以获得如下SDP凸优化问题[14]

(27)
式中:±表示半正定运算符。
式(27)将加权最小二乘转换为一个带线性等式约束和线性不等式约束的半定规划问题。可以通过使用凸优化中的内点法IP(Interior Point)如SeDuMi[15]进行求解,进而得到联合TDOA-AOA的凸优化问题的最优解,从而完成对目标节点的定位。
3 参考节点有误差时的半定规划(SDP)定位算法
在无线传感器网络的构建和应用中,参考节点的真实位置不一定已知,为了节约能量消耗,其位置也是由测量或者其他定位方案获得,存在一定的误差,因而会对未知节点的定位精度产生影响。本节通过分析误差项并引入SDP算法减小位置误差对定位精度的影响。
设第i个带误差的参考节点位置为
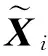
(28)
ΔXi=(nxi,nyi)T
(29)
根据近似等价条件[16],可得
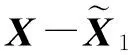
(30)
式中:ρa,b=(a-b)/‖a-b‖表示从b指向a的单位向量。将(28)、(30)代入(10),保留Δxi的线性项,有
(31)
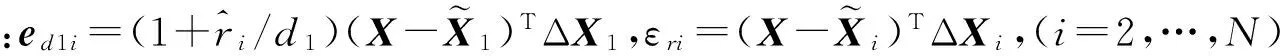
(32)
式中:εθi=[sinθicosθi]ΔXi,(i=1,…,N)
合并式(31)和式(32)得

(33)
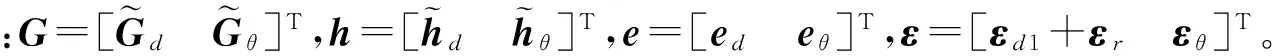
权矩阵可以表示为

(34)
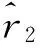
(35)
(36)
(37)
(38)
(39)
(40)
与上一节类似,我们可以推导出参考节点有误差时的半定规划(SDP)定位算法:
(41)
(42)
(43)

4 SDP算法的仿真分析
本节中我们将通过MATLAB对提出的联合定位算法进行2 000次蒙特卡洛仿真试验,并与已有的二维空间TDOA-AOA联合定位算法进行对比。使用位置均方根误差(RMSE)来对算法进行对比评价。RMSE的表达式如下。
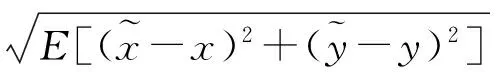
(44)

4.1 参考节点无误差的定位结果分析
首先考虑有5个参考节点,其坐标分别是(0,0)m,(260,150)m,(0,300)m,(-260,150)m 和(200,-150)m。待定位目标节点位于(50,100)m。图1为3种算法随TDOA测量距离方差σd的变化曲线图,其中AOA角度方差固定为σθ=1°。从图1可以看出,在TDOA方差较小时,SDP算法明显好于CWLS算法,与two-step LS基本一致,而在TDOA方差较大时,本文中的算法定位性能明显优于其他两种算法。图2中固定σd=3 m,3种算法随AOA测量角度方差σθ的变化情况。可以很直观地看出本文提出的算法定位效果最好。

图1 角度方差为1°时不同算法的定位性能比较
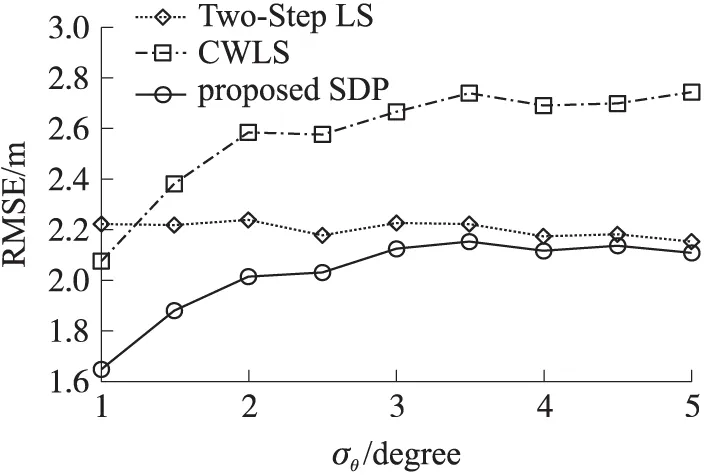
图2 距离方差为3 m时不同算法的定位性能比较
为了更有效地说明本文算法定位特性优于其他算法,我们进行了CDF曲线对比,如图3所示,其中设定σθ=1°,σd=3 m。从图中可以看出,在进行的2 000次仿真实验中,本文所提算法定位误差在2 m以内的概率接近80%,高于其他算法的60%,因此可以证明本文定位算法鲁棒性更好。

图3 不同算法估计误差的CDF曲线图
接着我们分析SDP算法在节点通信性能下降时的定位效果,考虑两参考节点下对目标节点的定位,参考节点位置设在(0,0)m和(260,150)m,待定位节点位置不变。此时,由于CWLS中拉格朗日乘子法在两节点下无法求得实根,算法失效;而Two-Step LS不能解出待定位节点坐标。图4为本文算法分别在角度测量方差为σθ=1°和σθ=3°时,随TDOA方差的变化曲线图。从中可以看出在即使在测量误差较大时,本文算法的RMSE也能控制在10 m内。

图4 两参考节点下所提算法的定位性能
4.2 参考节点有误差的定位结果分析
为了对参考节点有位置误差的定位效果进行分析,在参考节点真实位置加高斯白噪声,假设TDOA和AOA测量误差分别为σd=1 m和σθ=1°。
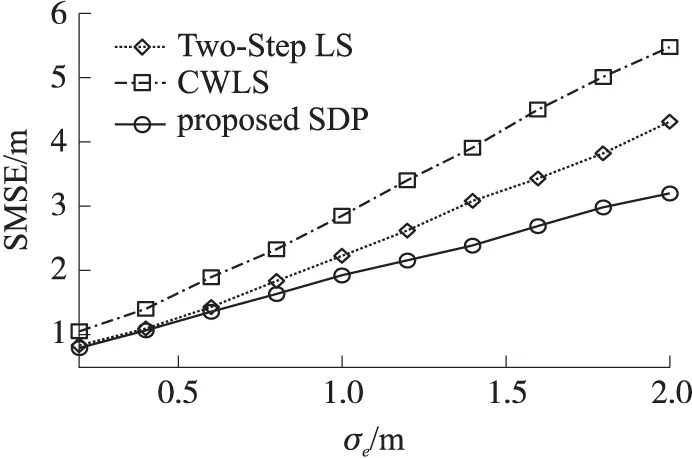
图5 不同算法随参考节点误差变化的定位性能比较
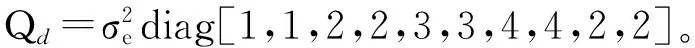
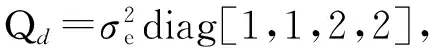
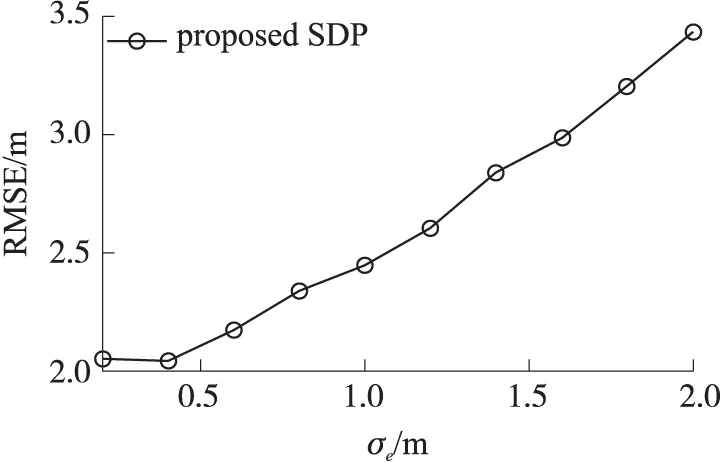
图6 两带误差参考节点下所提算法的定位性能
5 结束语
本文针对TDOA-AOA联合定位中传统加权最小二乘算法的非线性,通过闭式法求解会产生多个局部最优值的问题,提出一种基于SDP的凸优化定位方法。首先分析了传统的WLS联合定位算法;接着,通过推导将问题转化为非凸二次优化问题,之后引入冗余变量和SDR技术将问题转化为SDP凸优化问题,通过求解从而实现精确定位;同时,分析和推导了实际应用中参考节点有位置误差的情形。从仿真结果图中可以看出,本文算法在参考节点数目较多时定位精度高于已有算法,在仅有两个参考节点提供位置信息时,经典算法如Two-step LS和CWLS都失效,而本文算法还能够实现较高精度下的定位。
[1] Emokpae L E,DiBenedetto S,Potteiger B,et al. UREAL:Underwater Reflection-Enabled Acoustic-Based Localization[J]. IEEE Sensors Journal,2014,14(11):3915-3925.
[2] Tomic S,Beko M,Dinis R. RSS-Based Localization in Wireless Sensor Networks Using Convex Relaxation:Noncooperative and Cooperative Schemes[J]. IEEE Transactions on Vehicular Technology,2015,64(5):2037-2050.
[3] 姜志鹏,陈正宇,刘影,等. TOA定位算法非线性优化问题研究[J]. 传感技术学报,2015(11):1716-1719.
[4] Qiao T,Redfield S,Abbasi A,et al. Robust Coarse Position Estimation for TDOA Localization[J]. IEEE Wireless Communication Letters,2013,2(6):623-626.
[5] Shao H J,Zhang X P,Wang Z. Efficient Closed-Form Algorithms for AOA Based Self-Localization of Sensor Nodes Using Auxiliary Variables[J]. IEEE Transactions on Signal Processing,2014,62(10):2580-2594.
[6] 骆吉安,谭智文,郭云飞. 声纳阵列网络基于移动信标到达角的渐进最优节点自定位算法[J]. 传感技术学报,2016,29(3):403-410.
[7] Liu D,Liu K,Ma Y,et al. Joint TOA and DOA Localization in Indoor Environment Using Virtual Stations[J]. IEEE Communica-tions Letters,2014,18(8):1423-1426.
[8] Yang S H,Kim H S,Son Y H,et al. Three-Dimensional Visible Light Indoor Localization Using AOA and RSS with Multiple Optical Receivers[J]. Journal of Lightwave Technology,2014,32(14):2480-2485.
[9] Chan Y T,Chan F,Read W,et al. Hybrid Localization of an Emitter by Combining Angle-of-Arrival and Received Signal Strength Measurements[C]//IEEE 27th Canadian Conference on Electrical and Computer Engineering(CCECE),Toronto,ON,2014:1-5.
[10] Li C,Weihua Z. Hybrid TDOA/AOA Mobile User Location for Wideband CDMA Cellular Systems[J]. IEEE Transactions on Wireless Communications,2002,1(3):439-447.
[11] Cheung K W,So H C,Ma W K,et al. A Constrained Least Squares Approach to Mobile Positioning:Algorithms and Optimality[J]. EURASIP Journal on Advances in Signal Processing,2006,2006:1-24.
[12] Yin J,Wan Q,Yang S,et al. A Simple and Accurate TDOA-AOA Localization Method Using Two Stations[J]. IEEE Signal Processing Letters,2016,23(1):144-148.
[13] Chan F K W,So H C,Ma W K,et al. A Flexible Semi-Definite Programming Approach for Source Localization Problems[J]. Digital Signal Processing,2013,23(2):601-609.
[14] Luo Z,Ma W,So A,et al. Semidefinite Relaxation of Quadratic Optimization Problems[J]. IEEE Signal Processing Magazine,2010,27(3):20-34.
[15] Sturm J F. Using SeDuMi 1.02,a MATLAB Toolbox for Optimization over Symmetric Cones[J]. Optimization Methods and Software,1999,11(1-4):625-653.
[16] Liu Y,Guo F,Yang L,et al. An Improved Algebraic Solution for TDOA Localization with Sensor Position Errors[J]. IEEE Communications Letters,2015,19(12):2218-2221.

张文华(1991-),男,硕士研究生,天津大学电气自动化与信息学院,主要研究方向为无线传感器网络定位,zhangwenhua@tju.edu.cn;

于洁潇(1981-),女,副教授,博士,天津大学电气自动化与信息工程学院,主要研究方向为阵列信号处理,无线传感器网络定位技术等,yjx@tju.edu.cn。
JointTDOA-AOASourceLocalizationinWirelessSensorNetworksUsingSemidefiniteProgramming*
ZHANGWenhua1,YUJiexiao1*,LIUKaihua2,ZHAOYu1
(1.School of Electrical and Information Engineering,Tianjin University,Tianjin 300072,China; 2.School of Microelectronics,Tianjin University,Tianjin 300072,China)
Joint TDOA-AOA localization is able to improve location estimation accuracy through utilizing all the available information in wireless sensor networks(WSNs). Due to the non-linearity of the equations,joint weighted least square(WLS)may converge to local optimum solution when applied to wireless sensor networks localization. Therefore,by applying semidefinite relaxation(SDR)to the quadratically constrained quadratic program problem which is derived from WLS method,we transformed the joint localization problem into a low complexity semidefinite programming(SDP)problem to find the global optimum solution. Localization in the presence of sensor position errors has also been studied. Simulation results show that,compared with the existing approaches,the proposed approach has higher accuracy whether with or without sensor position errors. Furthermore,the proposed SDP method still has good performance with only two sensors offering location information.
wireless sensor networks;source localization;TDOA;AOA;semidefinite programming
项目来源:国家自然科学基金项目(61501322)
2017-02-16修改日期:2017-04-17
TP393.0
:A
:1004-1699(2017)09-1375-06
10.3969/j.issn.1004-1699.2017.09.013
