一种数字磁罗盘全罗差自主优化补偿方法

洪琪璐,张爱军*,王昌明

(南京理工大学机械工程学院,南京 210094)

一种数字磁罗盘全罗差自主优化补偿方法

洪琪璐1,张爱军1*,王昌明2

(南京理工大学机械工程学院,南京 210094)

为了进一步提高数字磁罗盘全姿态罗差补偿精度,提出了一种基于地磁场分量的罗差自主优化补偿方法。从罗差补偿模型出发,分析椭球拟合补偿方法的局限性,在对参数缺失和剩余误差分析的基础上,建立了包含缺失参数的优化补偿模型;针对非线性优化模型引入粒子群算法PSO(Particle Swarm Optimization)对模型参数进行估计,数值仿真结果证明了算法可有效估计缺失参数。实验结果表明,优化补偿过程无需借助外部辅助姿态信息,俯仰角-20°姿态下,优化补偿方法在椭球假设补偿基础上将其最大误差由4.8°降至1.9°,误差标准差由1.5°降至1.1°。

数字磁罗盘;全罗差;非线性;粒子群算法

数字磁罗盘是一种利用地球磁场与重力加速度实现航向测量的工具,由于其捷联特性和体积、精度等方面的优势已被广泛应用于导航定位系统中。在实际应用中,磁罗盘极易受到载体周边杂散磁场地干扰,造成较大的磁航向测量误差(罗差),为实现高精度、高可靠性的导航与定位,必须对磁罗盘罗差进行有效的校正。在众多的罗差补偿方法中,Moulin M等[1]提出的罗差椭球假设补偿方法具备的全姿态范围罗差的补偿能力,且无需依赖外部辅助姿态信息、自主补偿能力较强,在实际工程中被广泛应用并得到国内外学者进一步的深入研究。文献[2-3]基于泊松模型,分析椭球假设理论的正确性,采用最小二乘椭球拟合算法求取模型参数,计算量小。文献[4]提出了带约束的最小二拟合算法,保证拟合椭球算法的稳定性。但文献[2]指出椭球假设方法存在辨识参数缺失的问题,椭球假设可以很好地辨识出硬磁干扰系数,但对软磁干扰系数矩阵非对角元素的辨识能力不足,剩余的非对准误差造成了较强非线性的罗差。文献[5]也证明了椭球假设存在软磁干扰系数矩阵非对角元素存在相互耦合的问题,而采用椭球假设方法对非对准误差是不可观测的,需要进一步设计优化方法补偿非对准误差。虽然文献[6-8]提出的十二位置标定法、递推最小二乘法、最大似然估计法、遗传算法均可实现对非对准误差的补偿,但需要重新借助外部辅助姿态信息,原有椭球假设方法的自主补偿优势不再。非对准误差可以看为安装误差的一种来进行补偿[9]。文献[10]借助外部平面的约束对安装误差进行补偿,但需要多次使用最小二乘法提高拟合精度,过程繁琐。

在前人工作的基础上,本文提出了一种融合磁罗盘自身姿态信息的自主优化补偿方法。在椭球假设补偿的基础上,方法仅利用磁罗盘自身输出的信息一步估计出剩余缺失参数并对非对准误差进行修正,从而进一步实现罗差优化补偿,同时整个优化补偿过程无需借助外部姿态信息。仿真实验与实物实验的结果均证明了本文提出优化方法的正确性和有效性。

1 罗差模型与补偿分析

1.1 罗差模型

定义Hb=[Hbx,Hby,Hbz]T为地球磁场在载体坐标系下的分量,Hm=[Hmx,Hmy,Hmz]T为三轴地磁传感器实际测量值。地磁传感器受到载体铁磁物体影响,其敏感的磁场强度为地磁场与载体杂散干扰磁场叠加的总和,根据矢量叠加原理:

Hm=Hb+KHb+ξ

(1)

令A=K+I3×3,变换式(1)可得:

Hb=A-1(Hm-ξ)

(2)

式即为地磁传感器的误差补偿模型,若能确定A-1,ξ,就能由地磁传感器测量值计算地磁场强度在载体坐标系上的分量,由式(3)、式(4)计算出真实的磁航向ψ。

Ht=R(θ,γ)Hb

(3)

ψ=arctan(Hty/Htx)

(4)

式中:Ht为Hb在当地水平坐标系中的投影,θ、γ为磁罗盘输出俯仰角与横滚角,R(θ,γ)为对应的旋转矩阵。

1.2 罗差模型

在固定的空间位置,地磁场矢量的模的长短不变时,根据式(2)可得:

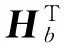
(5)

式中:L=(A-1)TA-1。式(5)表示了一个有关自变量Hm的椭球方程,表明Hm测量值轨迹为一椭球。采集多组测量值,通过最小二乘拟合等方法确定椭球方程解出L与ξ。矩阵A-1进一步由L求出,此后通过由式(2)即可完成罗差补偿。

A-1可通过分解正定矩阵L来确定。目前对于矩阵L分解方法,有Cholesky分解、极分解、奇异值分解等[2,4],但各类分解方法得出的矩阵A-1并不一致。针对上述情况进行分析,假定存在一个任意的正交矩阵Q,使得R=QA-1,则有:

RTR=(A-1)TQA-1=(A-1)TQTA-1=(A-1)TA-1=L

(6)

由式(6)可见,各种分解方法得出的矩阵之间必会相差一个正交矩阵。几何意义上,正交矩阵Q的存在相当于将补偿后地磁场测量轴系相对于较重力加速度测量轴系旋转了一定角度,引入了轴系间的非对准误差。文献[2]中实验证明了非对准误差的存在会造成较强的非线性罗差。

(7)

2 优化补偿方法设计

由前文分析可知,进一步优化罗差补偿精度的重点在于确定正交矩阵Q。固定空间位置,地磁场矢量的模长与方向均不变,因此其竖直分矢量与水平分矢量均为常矢量,如图1所示。以地磁场强度竖直分矢量Htz为例:

Htz=F(θ,γ)Hb=F(θ,γ)QHs

(8)

式中:Hs=A′-1(Hm-ξ)为椭球假设补偿后的三维地磁数据,F(θ,γ)=[sinθ,-cosθsinγ,cosθcosγ]T为旋转矩阵R(θ,γ)中第3行行向量。显然若矩阵Q缺失,式(8)必不成立。因此通过采集多组θ、γ和Hs利用式(8)中Htz固定不变的约束可以确定矩阵Q。根据空间轴系的旋转关系,将Q简化3参数的方向余弦矩阵,如式(7)所示。那么式(8)表示为一个关于参数β1、β2、β3的非线性方程,估计出该参数方程,即可由式(7)确定误差矩阵Q,矩阵A-1则唯一确定:A-1=QA′-1,从而完成优化补偿。

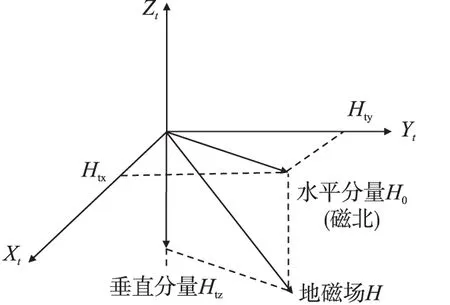
图1 地磁场在水平坐标中投影示意图

对于非线性参数方程,通常通过求导进行泰勒级数展开将其转化为线性方程,然后应用最小二乘法迭代进行求解,但算法极易受选取的初值影响而发散,且实际工程中初值选取也较为困难。粒子群算法PSO(Particle Swarm Optimization)是一种基于群体智能的优化算法,通过种群个体之间的相互协作与竞争,实现求取最优解,和其他算法相比,PSO代码量小,易于实现,尤其对初值要求不高,且具备全局收敛性,在实际工程中被广泛使用[11]。本文也引入该种方法对式(7)中参数进行估计,设计PSO估计步骤如下:

①由式(8)构造以下函数:

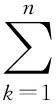
(9)

式中:ζ=(β1,β2,β3)T为待估计参数向量,k为测量序列,n为磁罗盘数据采样点个数。L(ζ)越小说明Htzk越接近于真实地磁场竖直分量Htz,最小时则认为ζ收敛于真值,因此设计的目标函数为:

F(ζ)=minL(ζ)

(10)

式(10)表示ζ是在使n个采样点Htzk的统计值L(ζ)最小时的参数值。

②满足βij～U[βmin,βmax],Vij～U[Vmin,Vmax]条件,随机给定微粒初始位置βij与初始速度Vij,i=1,2,…,M,j=1,2,3,M为种群大小。初始个体适应度pbesti与全局最优适应度gbest。

(11)

③更新微粒的速度与位置。

(12)

式中:t为当前进化代数,r1、r2为均匀分布于(0-1)区间的随机数,ω为惯性权重,c1、c2为加速因子。

④更新pbesti、gbest,若达到最大进化代数或满足精度标准,搜索终止;否则执行步骤②。

3 仿真验证与分析

为了验证方法的有效性与正确性,采用仿真数据进行实验。参考WMM世界地磁模型中南京地区的地磁场参数,定义磁倾角为48.12°,地磁场总量为50 000 nT,软磁干扰误差矩阵与硬磁干扰误差向量分别为:

(13)

参照以上给定参数生成了240组的三维干扰磁测数据,同时为模拟传感器测量噪声,在三维磁场数据和θ、γ数据上分别叠加满足零均值分布,标准差分别为30 nT和0.1°的高斯噪声。生成磁场测量数据三维显示如图2所示,图2中球面为理论地磁场的测量圆球面。

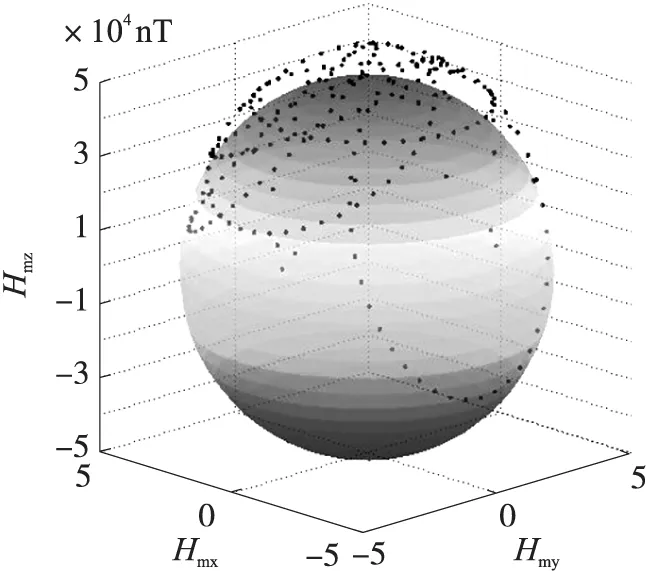
图2 仿真数据三维分布图

首先使用最小二乘椭球拟合方法求解误差模型参数,并采用常见的上三角、下三角与对称矩阵3种形式软磁干扰矩阵对地磁场测量数据修正,然后在此修正数据基础上运用本文提出的优化方法对剩余的非对准误差角β进行估计。其中PSO参数取值,M、ω、c1、c2分别为40、0.5、2、2。表1为误差角ζ(°)估计结果。

表1 不同分解情况下非对准误差角估计值

由表1可知:ζ估计值与理论值基本一致,表明优化方法可以有效地估计缺失参数。

为验证优化方法磁航向补偿精度,采用表1中β估计值优化后的软磁干扰矩阵,对俯仰角-30°倾斜姿态处旋转采集的地磁数据进行修正,并与椭球假设方法的补偿结果进行对比,对比结果如图3所示。图3中,由于在不同形式软磁干扰系数矩阵修正数据基础上进行优化补偿后的结果非常接近(<0.1°),因此使用一条曲线表示(“优化后”所对应曲线)。由图3可知,补偿前磁航向剩余误差的范围较大,椭球假设补偿后误差范围减小,同时不同矩阵形式的补偿效果不相同,使用优化补偿方法进一步补偿后的误差范围明显小于椭球假设法。

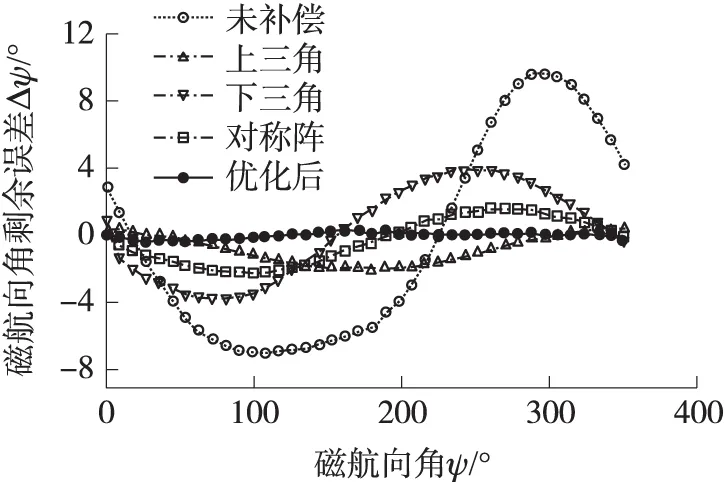
图3 磁航向误差补偿比对图

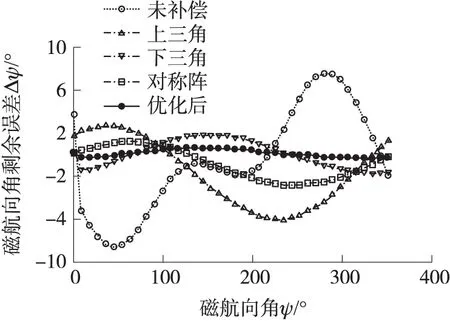
图4 不同软磁干扰情况磁航向误差补偿结果

而椭球拟合方法补偿精度的不一致性有:上三角形式>对称阵形式>下三角形式,以地磁场测量轴系的x轴与z轴进行分析。如式(13)所示,软磁干扰系数矩阵A的上半部分对角元素的数值明显大于其下半部分对角元素的数值,相比x轴误差对z轴的影响,z轴误差对x轴影响要大得多。而下三角矩阵将上半部分对角元素数值设置为0,忽略了z轴误差对x轴影响,故其补偿精度最差,而上三角矩阵补偿精度最高。图4给出了矩阵A的上半部分对角元素的数值小于其下半部分对角元素的补偿情况,可以明显看出此时下三角形式补偿效果好于上三角形式。由于实际应用中无法预知软磁干扰矩阵接近于何种矩阵形式,而较难选取适合形式使得椭球假设方法的补偿效果达到最佳,这也是实际应用中椭球假设方法的局限性所在。

4 实验验证

为了验证本文提出优化方法的实际性能,利用PNI公司的TCM-XB数字磁罗盘在三轴转台上进行实验,磁罗盘内部加速度计实验前已进行标定,姿态测量精度±0.2°,转台角度分辨率为0.01°。实验前,将钢铁构件固定于磁罗盘附近,用于模拟产生载体干扰磁场。由于实际中数字磁罗盘的应用对象不会产生较大幅度的倾角,因此实验设计θ、γ的变化范围为±45°。

实验步骤:在水平与俯仰角±20°、±40° 5种姿态下分别旋转一周采集地磁场数据与姿态数据,间隔15°,同时在姿态范围内随机采集40组数据,共160组;按算法计算分别椭球假设模型参数与优化补偿模型参数,然后按前文步骤对以上地磁数据进行修正,以转台输出的航向作为标准角度计算磁航向剩余误差。为了方便说明,以俯仰角为-20°的倾斜姿态为例,如图5所示。

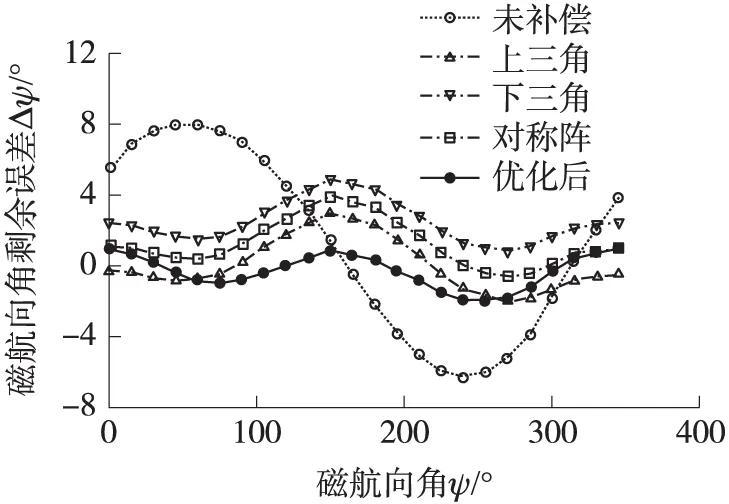
图5 俯仰角-20°时磁航向误差补偿结果

图5中,未补偿时磁航向最大误差达到7.8°,误差标准差5.15°;椭球假设方法中,软磁干扰矩阵取上三角形式时补偿效果最佳,最大误差2.9°,标准差1.2°,取下三角形式最差,最大误差4.8°,标准差1.5°;优化补偿后磁航向最大误差进一步减小到1.9°,标准差减小到1.1°。

5 结论

应用于数字磁罗盘的全姿态罗差补偿方法存在着一定局限性,补偿精度受到制约,本文在分析局限性的基础上提出了一种罗差自主优化补偿方法。仿真结果表明,常规椭球假设补偿方法估计参数存在缺失,不同分解形式的软磁矩阵的补偿效果不一致,而优化补偿方法能够有效估计3个缺失参数,唯一确定原模型中的12参数。实物实验结果显示,倾角20°姿态下,优化方法将常规椭球假设方法补偿的最大误差由4.8°降至1.9°,误差标准差由1.5°降至1.1°,提出的优化方法有效估计椭球假设方法中剩余非对准误差,进一步提高磁航向补偿精度。

本文提出的优化方法参考水平坐标系中地磁场分量这一自然基准,利用分量不变性的约束估计出缺失参数,而无需借助外部辅助姿态,保持了椭球假设方法原有自主补偿的优势,可用于磁罗盘现场校正的场合。

[1] Moulin M,Guodon J C,Marsy J M,et al. Process for Compensating the Magnetic Disturbances in the Determination of a Magnetic Heading,and Devices for Carrying Out This Process. United States:No.4414753,1983-11-15.

[2] 李智,李翔. 基于椭球假设的三轴电子罗盘罗差补偿研究[J]. 仪器仪表学报,2011,32(10):2210-2215.

[3] Pylvänäinen T. Automatic and Adaptive Calibration of 3D Field Sensors[J]. Applied Mathematical Modelling,2008,32(4):575-587.

[4] Fang J,Sun H,Cao J,et al. A Novel Calibration Method of Magnetic Compass Based on Ellipsoid Fitting[J]. IEEE Transactions on Instrumentation and Measurement,2011,60(6):2053-2061.

[5] 刘玉霞,周军,葛致磊. 基于轨迹约束的地磁场测量误差修正方法[J]. 中国惯性技术学报,2012,20(2):205-210.

[6] 郭鹏飞,任章,邱海韬,等. 一种十二位置不对北的磁罗盘标定方法[J]. 中国惯性技术学报,2008,15(5):598-601.

[7] 郭鹏飞,华春红,任章,等. 基于递推最小二乘的航姿系统罗差校正[J]. 中国惯性技术学报,2008,16(1):24-27.

[8] 龙礼,张合,刘建敬. 姿态检测地磁传感器误差分析与补偿方法[J]. 中国惯性技术学报,2013,21(1):80-83.

[9] Bonnet S,Bassompierre C,Godin C,et al. Calibration Methods for Inertial and Magnetic Sensors[J]. Sensors and Actuators A:Physical,2009,156(2):302-311.

[10] 范成叶,李杰,陈文蓉,等. 电子罗盘安装误差标定与补偿方法研究[J]. 传感技术学报,2013,26(5):622-626.

[11] 焦巍,刘光斌,张金生,等. 基于粒子群算法的地磁匹配航迹规划[J]. 系统工程理论与实践,2010,30(11):2106-2111.

洪琪璐(1990-),女,浙江金华人,现为南京理工大学仪器仪表工程专业在读研究生,主要研究方向为无线通讯技术,xichexue@yeah.net;

张爱军(1978-),男,黑龙江庆安人,博士,副教授,主要研究方向为导航信息处理技术、嵌入式开发、超高频无线射频技术。

MethodtoMagneticDeviationSelf-OptimalCompensationofDigitalMagneticCompass

HONGQilu1,ZHANGAijun1*,WANGChangming1

(School of mechanical Engineering,Nanjing University of Science and Technology,Nanjing 210094 China)

A magnetic deviation self-optimal method based on thecomponent of geomagnetic field was put forward to improve the compensation precision of all-attitude digital magnetic compass. According to magnetic deviation compensation model,a limited compensation ellipsoid matching error wasanalyzed and an optimal compensation model including missing parameters was established based on the missing parameters andresidual error analysis. In view of the nonlinear optimal model,the particle swarm optimization(PSO)was introduced to estimate the model parameters,and the results of numerical simulation was proved that the PSO couldbe estimated the missing parameters effectively. All experiment results showed that the process of optimal compensation did not need external auxiliary posture information. When the pitching angle was -20°,the maximum error was reduced from 4.8° to 1.9° and the standard deviation was reduced from 1.5° to 1.1° in the usage of optimal compensation method based on ellipsoid matching error compensation method.

digital magnetic compass;magnetic deviation;nonlinear;PSO

2017-03-01修改日期:2017-06-05

U666.1

:A

:1004-1699(2017)09-1364-05

10.3969/j.issn.1004-1699.2017.09.011