基于近邻参考集与E2LSH加速的姿态敏感器故障检测
2017-09-22王慧泉金仲和杜超禹
王 婵,王慧泉,金仲和,杜超禹
(浙江大学微小卫星研究中心,杭州 310027)
基于近邻参考集与E2LSH加速的姿态敏感器故障检测
王 婵,王慧泉*,金仲和,杜超禹
(浙江大学微小卫星研究中心,杭州 310027)
为满足高维、多状态姿控敏感器遥测数据的实时故障检测,提出了一种基于局部敏感哈希和子空间异常因子的故障检测算法。算法通过局部敏感哈希索引的建立和使用,检测全局故障点;通过子空间异常因子的计算,检测子空间故障点。提出了近似邻近参考集与缓存桶的概念,降低算法的时间复杂度。ZDPS-2卫星的姿控敏感器数据分析结果表明,该方法故障查准率89.3%,查全率100%,且泛化性能优于原始的子空间异常程度算法。该算法解决了原始的子空间异常程度算法实时性低、检测全局故障困难问题,可以满足姿控敏感器实时故障检测需求。
姿态敏感器;故障检测;近邻参考集;局部敏感哈希
姿控系统ADCS(Attitude Control System)是卫星最重要的子系统之一。通过读取姿态敏感器的采样信息,姿控系统实时解算卫星姿态,并将其作为控制回路的输入,使卫星姿态满足一定的指向需求[1]。姿控系统包含多种敏感器(太阳敏感器[2]、地球敏感器[3]、陀螺仪、磁强计等),其数据的准确性对卫星的姿态保持有十分关键的意义。
目前国内外基于专家系统或知识库的姿控等子系统故障检测研究较多[4-7],即通过建立故障现象和故障源的关系模型,进行故障检测。这类方法可以准确获得故障诊断结果,但只能发现已知的部分故障,且需要大量先验知识。而数据驱动的故障检测算法可以发现已知和未知的故障[8]。Martinez[9]和Omeara[10]等人采用局部异常概率算法LoOP(Local Outlier Probabilities),根据数据的趋势变化适应性地发现卫星遥测数据的异常。但这类算法局限于单维数据分析,对集体故障、关联故障等故障形式的检测存在困难。文献[11]提出了一种针对高维的姿控敏感器数据故障检测方法,通过姿控系统数据的固有冗余关系是否保持作为判断故障类型的依据。方法利用主成分分析PCA(Principal Component Analysis)将敏感器空间划分为主成分子空间和残差子空间,通过统计量监控两个子空间实现故障检测,但仅针对自旋稳定的卫星状态,无法满足如对地稳定、对日稳定等不同卫星状态的需求。
Kriegel等[12]设计实现了一种适应多维数据的SOD(Subspace Outlier Degree)算法,通过近邻数据与被检测点的子空间差异程度判断被检测点是否异常,适合于在多维数据中发现子空间异常。由于不同的卫星状态下敏感器数据的欧氏距离较大,参考集之间不会互相影响。但该算法存在两个问题,其一,由于算法时间消耗过高,时间复杂度为O(n2),无法用于实时姿态敏感器故障检测;其二,算法没有针对全局故障点的处理办法。
本文实现了一种基于E2LSH(Exact Euclidean Local Sensitive Hash)加速的SOD的算法。通过近似共享近邻与缓存桶机制,本文解决了原始SOD算法实时性低的问题;通过E2LSH算法的引入,解决了检测全局故障困难的问题,满足了姿控系多维敏感器数据的实时故障检测的要求。
1 姿控系统多维敏感器的故障检测
姿控系统多维敏感器的故障检测通过基于E2LSH的SOD故障检测算法实现。
故障检测过程包括:基于E2LSH的索引生成,基于近似共享近邻的参考集建立,异常程度计算。如图1所示。
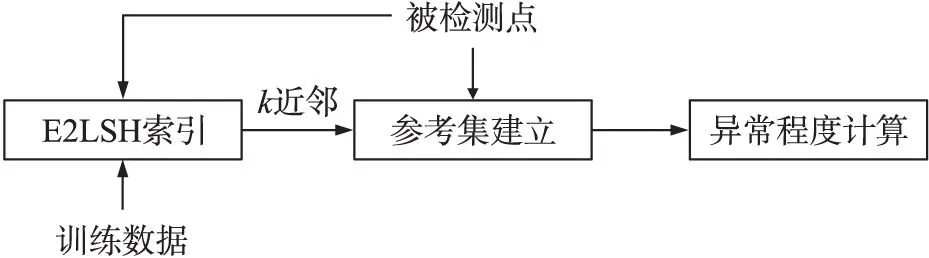
图1 姿态敏感器实时故障检测系统的结构
1.1 索引生成
基于p-stable的局部敏感哈希E2LSH(Exact Euclidean LSH)是一种基于二值的哈希编码算法,实现了高维k近邻问题的随机化解决方法,即(r,1+ε)近邻点p被报告的概率至少为1-ε[13]。
E2LSH算法在应用到姿态敏感器数据时,首先将部分姿控系统在测试或实际工作时的敏感器数据作为训练集,建立姿控系统k近邻的初始索引源。对数据X=[x1,x2,…,xn]∈Rd×n采用的哈希函数族
ha,b(x)=(ax+b)/ω
(1)
式中:a是一个d维的向量,向量的每一个值是从p-stable分布中随机独立选取的一个实数,b是从[0,ω]范围内均匀分布中随机独立选取的一个实数,ω是人工确定的参数,根据数据的范围选择。
哈希表由q个独立选取的哈希函数族组成,
g(x)=[h1(x),h2(x),…,hq(x)]
(2)
哈希表可以将一个d维的数据映射到一个q维的钥匙(key)。每个哈希key值对应一个哈希桶。相同哈希桶中的点,具有近邻特性。在建立索引时,一般选择多个哈希表,使近邻点在某个桶中相撞的概率增加。到k近邻查找阶段,只需要计算相同桶中的数据的距离,相比线性暴力的距离计算和搜索,时间复杂度较低。
q值的选取与k近邻查找时间相关。查找时间分为两部分,查找桶和桶内距离计算时间。其中查找桶的时间随着q值增大而增大,桶内距离计算时间随着q值增大而减少。在选择q值时,考虑两者相加的最优解,由于数据的分布不同,需要多次试验。
在建立索引时,选择多个哈希表
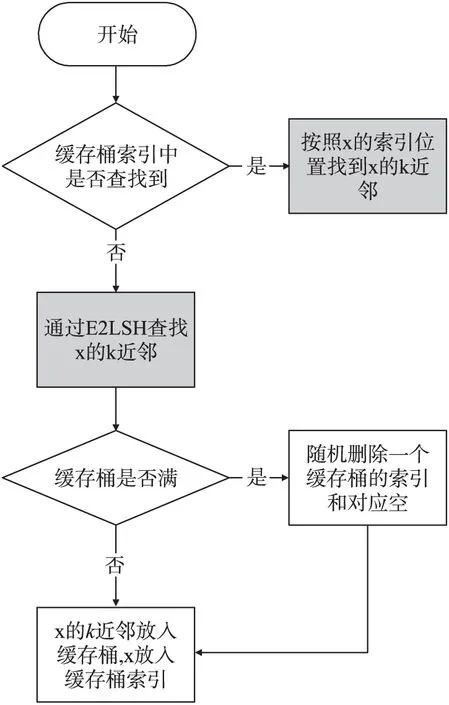
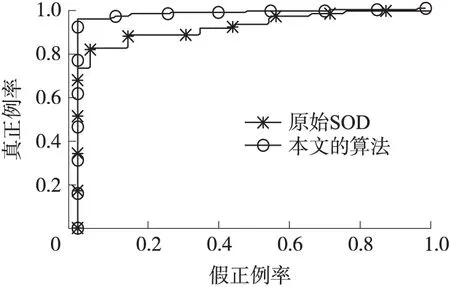
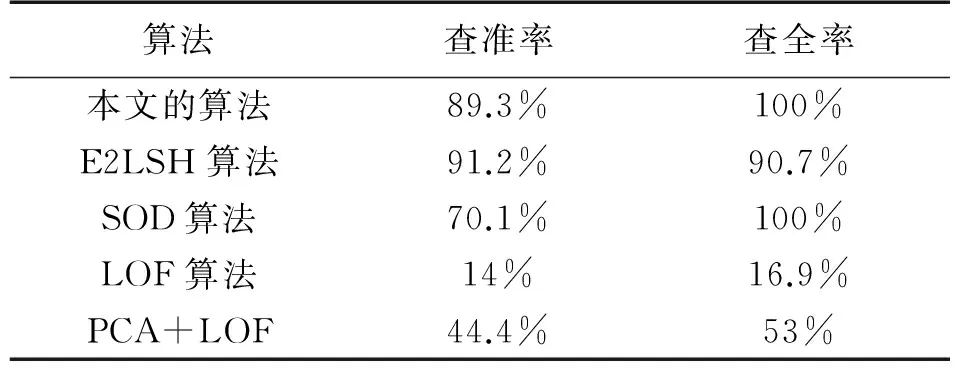
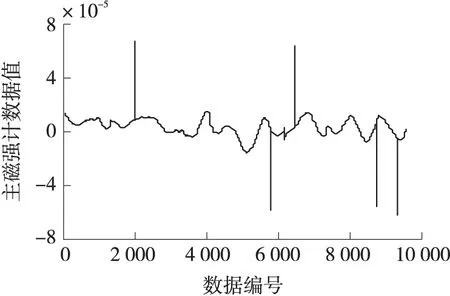
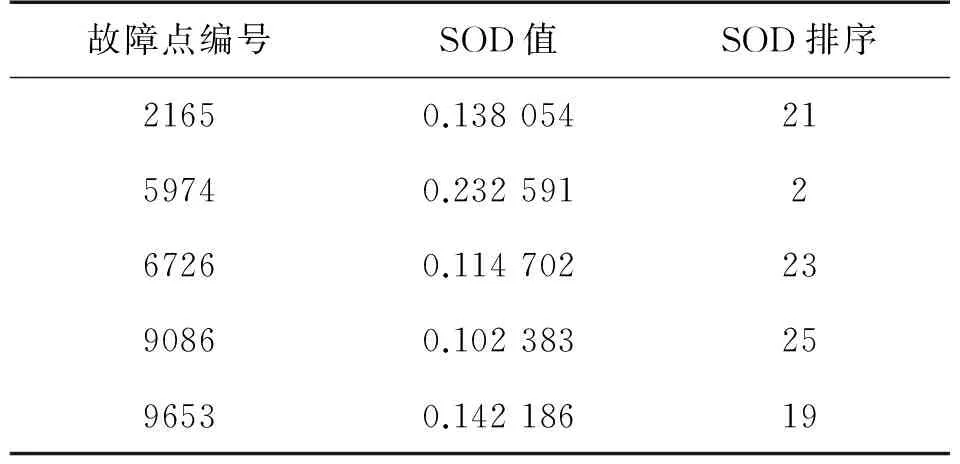
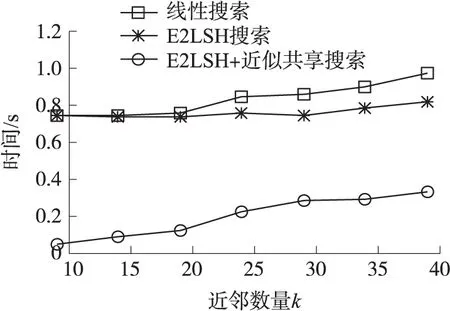
gi(x),1 (3) 1.2 参考集建立 共享近邻的计算需要获得所有数据点的k近邻并依次比较,无法适应动态的姿态敏感器故障检测,因此我们提出了建立近似共享最近邻和k近邻缓存桶的方案。 针对数据点xi,近似共享最近邻查找过程如下: Algoritm 1xi的近似共享近邻查找 1:通过E2LSH索引,查找xi的k近邻knnForXi 2:forxj∈knnForXi 3:查找xj的k近邻knnForXj 4:k2nnForXi=[k2nnForXi,knnForXj] 5:end for 6:forxh∈ unique(knn2ForXi) 7:查找xh的k近邻knn ForXh 8:end for 9:forxh∈ unique(knn2ForXi)&xh!=xi 10:If两个点xi和xh不在对方的k近邻中then 11:Similarity(xi,xh)=0 12:else 13:Similarity(xi,xh)=共享的近邻个数 14:end if 15:end for 16:共享近邻个数排序,选择共享近邻个数最多 的k个点作为参考集S(xi) *1~5步找出xi的可能共享近邻,6~9找到潜在共享近邻的k近邻,方便10~15通过比对获得共享的近邻个数(第13步)。 近似共享近邻算法是在最多k2个数据点的范围内查找xi的k个共享近邻,相比遍历所有数据点暴力查找共享近邻,时间复杂度大为降低,从O(n)降低为O(k2),其中k2≪n。经30维独立高斯分布随机数据集计算发现,近似共享最近邻与暴力搜索的结果相同程度达到93.3%,而对姿态敏感器数据实际集,这个数值达到了91.75%。 考虑姿控敏感器数据的实时检测,时间序列上接近的数据点存在连续性,前一点和后续点的k近邻存在重复,我们提出了缓存桶的概念。将最近查找的的k近邻的数据位号放置在缓存桶中,可重复提取,相比E2LSH查找更快速。增加缓存桶后查找数据点的k近邻过程如图2所示。 图2 增加缓存桶的k近邻查找过程 缓存桶的容量B一般设置为k2或稍小,在ZDPS-2卫星敏感器数据的处理中,针对30-近邻的缓存桶的命中超过55%,近似节省55%时间消耗。 缓存桶和近似共享最近邻的概念提出,使时间复杂度和空间复杂度能满足动态姿态敏感器数据的故障检测要求。 1.3 异常程度计算 SOD算法擅长发现子空间的故障情况,但在实际应用中存在的故障包括了全局故障和子空间故障,全局故障数据点的表现形式为该点与所有点的欧式距离都很大,在查找这类点的k近邻时,SOD算法需要花费更多的时间,因此我们分情况处理数据点的故障检测。 全局故障点,在E2LSH的查找过程中表现为所有哈希表对应的桶中数据稀疏。对桶中数据和少于h的点,认为其近邻区域没有足够的数据,离所有数据点都很远,为全局故障(h=当前数据点总数/E2LSH的查找桶的个数)。全局故障点,在k近邻查找阶段直接划入故障点范围,其异常程度值(SOD值)记为1。 子空间故障点,按照SOD过程计算[12]。在参考集范围S(xi)内,计算单维属性方差期望: (4) 式中 (5) 然后通过判断数据的单维属性方差大小,建立子空间定义向量(subspace defining vector)vS(xi): (6) 式中:α是事先定义的参数,一般取0.8~1.5。 最终得到xi点的子空间异常程度值(SOD值): (7) SOD在算法内考虑了“高维诅咒”的解决方法,参考集的选择上采用了共享近邻作为相似性依据。相比聚类等非0即1的算法,SOD算法的结果是介于0到1的程度值,更符合实际。将全局故障点在SOD计算中筛选可以极大的提升故障检测的效率。 本文在MATLAB R2010b,采用ZDPS-2姿控系统敏感器数据作为测试集,对加速SOD异常检测算法(共享近邻点的数量=30)进行了性能研制。训练集DS0包括30维数据,共9 898个点,其中已知故障的数据点全局故障点205个,子空间故障点21个。 SOD是一种通过程度值预测故障的算法,我们采用ROC(Receiver Operating Characteristic)曲线评价算法的泛化性能,如图3所示。本文提出的故障检测算法曲线能包住原始SOD算法的曲线,说明其泛化性能稍好于原始SOD算法。其主要原因是全局故障点SOD值提前判定为1,准确度相对更高。 图3 ROC曲线(本文的算法和原始SOD) 本文采用查准率和查全率作为故障检测结果的另一对性能评价方法。仅考虑全局故障点,本文提出的故障检测算法的查准率为91.2%,查全率为100%。子空间故障点方面,采用Grubbs标准预测SOD值是否异常,查准率为71.4%,查全率100%。本文算法的综合查准率和查全率对比E2LSH,SOD,LOF(Local Outlier Factor)[15],PCA+LOF算法,结果如表1所示。 表1 算法查准率与查全率对比 图4 主磁强计数据值 E2LSH适合于查找全局数据,而本数据集全局故障点比例较高,因此E2LSH算法效果较好。SOD算法实现了较高的查全率,但其查准率受到集中分布的故障点的干扰,相比本文的算法偏低。LOF算法表现不佳的原因是其基于密度与距离,受到了“高维诅咒”的影响。而加入PCA将数据降到1维,降维后包含原数据的41.26%的信息,查准率和查全率上升。由于本文的数据并不稀疏,经过降维后信息损失明显,检测效果较差。综上所述,本文提出的算法具有较全面的检测能力和均衡的查准率查全率。 以姿控敏感器数据中一列主磁强计(去除全局故障点)数据为例,如图4所示,主磁强计数据中存在一些跳变点。姿控敏感器数据中,这些跳变点所在位置其他属性正常,属于子空间异常,经Grubbs检测全部检出,跳变点的SOD值如表2所示。 表2 子空间故障点SOD值与排序 *SOD排序值越小越有可能属于故障 本文提出的故障检测算法时间消耗随共享近邻的数量k的变化曲线如图5所示,由于算法的主要时间复杂度由共享近邻搜索部分贡献,对比项采用线性搜索和仅采用E2LSH搜索的两项。本文提出的故障检测算法的时间消耗相比上述两项明显更低,但随k2线性增加。一般情况下,k2≪n。所以,本文提出的故障检测算法在时间复杂度上有较大的降低,在k取11时仅为0.06 s,本文使用的参数k值为21,时间消耗为0.1 s,可以满足姿控系统多维敏感器数据实时故障检测的要求。 图5 共享近邻搜索时间比较 本文提出了一种基于近邻参考集与E2LSH加速的姿控系统敏感器实时故障检测方法,相比SOD算法,本文在E2LSH加速的k近邻查找过程中,将发现的近邻稀疏数据判定为全局故障点,提高了检测效率和泛化能力。在参考集查找中,提出了近似共享近邻算法和缓存桶概念,时间复杂度从O(n)降低为O(k2),其中k2≪n,n为数据总量。在ZDPS-2姿控系统多维敏感器数据的验证中,相比SOD算法的时间消耗0.75 s/单点,该方法时间消耗仅0.1 s/单点,满足实时故障检测的要求。同时,本文提出的算法对姿控系统敏感器数据的故障点查准率89.3%,查全率100%,与原始的SOD算法和直接采用E2LSH算法的方式无明显差异,且泛化性能优于SOD算法。过程中成功发现主磁强计数据跳变的故障。该方法满足高维、多状态姿态敏感器故障检测的需求。 [1] 刘海颖. 微小卫星姿态控制系统关键技术研究[D]. 南京:南京航空航天大学,2008. [2] 白光耀,王昊,王志远,等. 面向微小卫星的全视场数字太阳敏感器设计[J]. 传感技术学报,2016,29(2):232-236. [3] 沈国权,王昊,郭振东,等. 面向微小卫星的红外静态焦平面地球敏感器设计[J]. 传感技术学报,2012,25(5):571-576. [4] 彭喜元,庞景月,彭宇,等. 航天器遥测数据异常检测综述[J]. 仪器仪表学报,2016,37(9):1929-1945. [5] 纪延琚. 卫星姿态控制系统层次化故障诊断系统设计与实现[D]. 哈尔滨:哈尔滨工业大学,2011. [6] 张盼盼. 基于支撑向量机的卫星姿控系统异变特征提取[D]. 北京:电子科技大学,2015. [7] Mizutani M,Hirose T,Takaki R,et al. ISACS-DOC:Monitoring and Diagnostic System for AKARI and HINODE[J]. Transactions of the Japan Society for Aeronautical and Space Sciences Space Technology Japan,2009,7(ists26):Tf_1-Tf_6. [8] Azevedo D R,Ambrosio A M,Vieira M. Applying Data Mining for Detecting Anomalies in Satellites[C]//Dependable Computing Conference. IEEE,2012:212-217. [9] Martinez J. New Telemetry Monitoring Paradigm with Novelty Detection[C]//Spaceops. 2012. [10] Omeara C,Schlag L,Faltenbacher L,et al. ATHMoS:Automated Telemetry Health Monitoring System at GSOC Using Outlier Detection and Supervised Machine Learning[C]//International Conference on Space Operations. 2015. [11] 李楠,张云燕,李言俊. 一种自旋稳定卫星姿态传感器数据异常的诊断方法[J]. 宇航学报,2011,32(6):1327-1332. [12] Kriegel H P,Ger P,Schubert E,et al. Outlier Detection in Axis-Parallel Subspaces of High Dimensional Data[C]//Pacific-Asia Conference on Advances in Knowledge Discovery and Data Mining. Springer-Verlag,2009:831-838. [13] Indyk,Piotr,Motwani,et al. Approximate Nearest Neighbors:Towards Removing the Curse of Dimensionality[J]. Theory of Computing,2015,604-613. [14] Datar M,Immorlica N,Indyk P,et al. Locality-Sensitive Hashing Scheme Based onp-Stable Distributions[C]//Proceedings of the Twentieth Annual Symposium on Computational Geometry. ACM,2004:253-262. [15] Breunig M M,Kriegel H P,Ng R T,et al. LOF:Identifying Density-Based Local Outliers[J]. Acm Sigmod Record,2000,29(2):93-104. 王婵(1990-),女,浙江大学微电子与固体电子学专业在读博士生,从事皮纳卫星遥测数据异常检测方面的研究; 王慧泉(1981-),男,浙江大学微小卫星研究中心副研究员,主要研究方向为MEMS/NEMS 传感器及其接口电路,微弱信号处理,微小卫星技术。 Real-TimeAttitudeSensorFaultDetectionBasedonNearestNeighborReferenceSetandE2LSHAcceleration WANGChan,WANGHuiquan*,JINZhonghe,DUChaoyu (Micro-Satellite Research Center,Zhejiiang University,Hangzhou 310027,China) Fault detection for satellite attitude sensors are required to handle high-dimensionality telemetry data and to manipulate faults in real-time. A new method based on exact Euclidean locality-sensitive hashing and subspace outlier degree is proposed to satisfy aforementioned requirements. The algorithm detects the global abnormal points by establishing and using the exact Euclidean local sensitive hash index. The subspace abnormal points are detected after calculating the subspace outlier factor. This paper presents the new concepts of approximate reference points and cache bucket to reduce the time complexity. The analysis for ZDPS-2 satellite attitude sensor data shows that,the precision is 89.3% and the recall is 100%. In addition,the algorithm’s generalization ability is superior to the original subspace outlier degree algorithm. The proposed method solves two problems of the original subspace outlier degree. It can satisfy the real-time and global abnormal points manipulation requirements of attitude sensors for the attitude control system. attitude sensors,fault detection,neighbor reference set,local sensitive hash 2017-01-27修改日期:2017-04-20 V448.2 :A :1004-1699(2017)09-1359-05 10.3969/j.issn.1004-1699.2017.09.010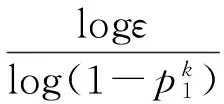

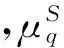
2 实验结果与分析
3 结论


