人工神经网络预测分析

高秀华　谢鹏芳　黄家荣

[摘要]文章基于四川省1978～2015年的国内生产总值（GDP）的经济增长数据，应用人工神经网络建立前5年的经济增长、第6年的相对时间与第6年的经济增长的关系模型，以实现用上5年的经济增长预测下1-5年的经济增长。研究结果表明，相对GDP的均方差函数nqse为1.26091×10^-5，相应的拟合精度为98%；全部预测年份（1983～2015）的平均预测精度为96%，表明预测值与实际值吻合程度很好，模型精度较高，建模简单。人工神经网络是预测区域经济增长的有效方法。

[关键词]四川省；GDP；人工神经网络；预测

GDP（Gross Domestie Product）即国内生产总值，是指一个国家内所有常駐单位在一定时期内生产的所有最终产品和劳务的市场价值，是衡量一个国家或地区经济状况和发展水平的重要指标。它不仅从整体上衡量一个国家或地区经济周期状态和经济波动，而且能从总体上衡量一个国家或地区的收入规模和国民产出。在宏观经济中，GDP是最受关注的经济数据，被认为是衡量宏观经济的运行状况、度量国民经济的发展状况的重要经济指标，也是政府制定经济政策、经济发展战略的重要依据。因此，文章参考相关研究，以四川省GDP为基础数据，用人工神经网络建立四川省经济增长预测模型，以实现对四川省GDP的准确分析、预测，为制定四川经济政策和发展战略的四川省人民政府提供科学依据，为关注、研究四川省宏观经济的人们提供参考。

一、材料与方法

（一）材料来源

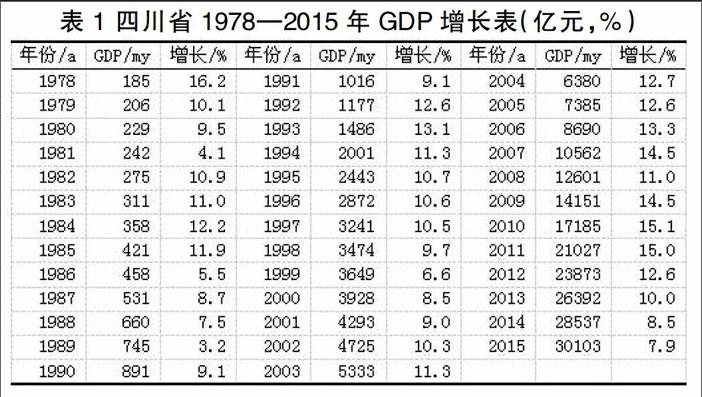
研究对象为四川省国内生产总值GDP，其统计数据来源于国家统计局，见表1。

（二）研究方法

GDP的预测方法主要是模型法。查阅近年的研究文献得知，已有研究中用于GDP预测的模型主要有时间序列分析模型ARIMA（p，d，q）、灰色系统模型GM（1，1）、回归模型、组合模型，极少应用或未很好应用具有独特优势的人工神经网络模型。本文将研究人工神经网络建立四川省GDP预测模型。人工神经网络模型有多种，如BP（Back Propagation）、RFB（Radla]Basis Function）、Hopfeld等等；用人工神经网络对GDP进行预测，可以分为单变量、多变量两种预测。本文将研究人工神经网络BP模型对四川省GDP的单变量进行预测。

1.构建模型

设四川省GDP单变量时间序列（G1）在前5年的取值均值（HG5）、第6年的相对时间（RT6）与第6年的取值（G6）之间有某种函数关系：

G6-f（MG5，RT6）（1）

公式中：f为某种函数关系，用BP模型表达这种函数关系，即用MG5，RT6作模型的输入变量，以G6作模型的输出变量，建立结构为2：t：1的人工神经网络BP模型如图1。

图1中，●、→、①、□、∫依次表示值为HG5和RT6的输入节点、信息流、值为1的输入节点、人工神经元、人工神经元的对数S型作用函数；w11，j为第1个隐层神经元与第j个输入节点之间的连接权；w21，1为输出层神经元与第1个隐层神经元之间的连接权；b1i为第1隐层神经元的阈值；b2为输出层神经元阈值。

公式中，logsig（）为MATLAB的对数S型作用函数；H1表示隐层第1个神经元的输出变量。该式即GDP的人工神经网络预测模型，在确定其中的权值、阈值等模型参数后，就可代入MG5和RT6预测G6。权值、阈值等模型参数的确定，需要用GDP的实际数据通过训练模型环节实现。

2.训练模型

训练模型，即以GDP数据标定模型中的权值、阈值等模型参数。先用前5年的GDP均值和第6年的相对时间为模型输入，以第6年的GDP为模型输出，即以1978～1982、1979～1983、……2010～2014年每5年GDP均值和1983、1984、……201 5的相对时间作为模型输入，以1983、1984、……2015各年的GDP依次作为各组输入对应的模型输出，构成33组模型学习样本；再用MATLAB的神经网络工具箱（nntool）训练所建模型。在训练过程中，按样本定义、样本导入、网络设置、网络训练、结果导出等5个步聚进行。为提高模型的训练效率，需要对表1中数据进行归一化前处理：每个GDP原值除以一个较大的数HD，它等于GDP最大值30103的1.8倍，其故见文末问题讨论。用归一化数据训练的模型，在模拟计算时，要作反归一化后处理。

二、结果与分析

（一）模型训练结果

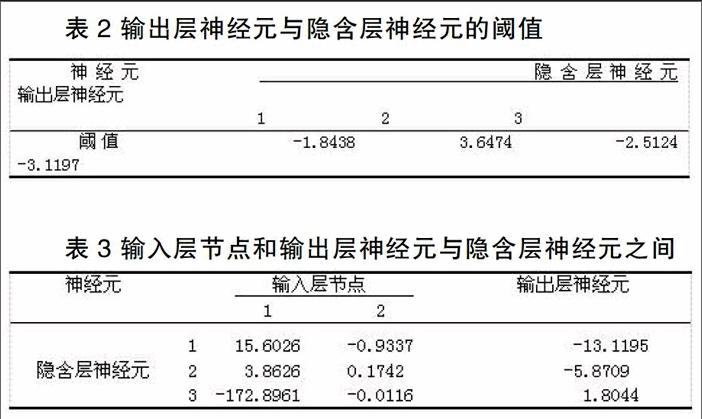
经反复试算分析，得出适合的隐含层神经元个数t为3，适合的神经网络模型结构为2：3：1，网络对象名取为SCGDP-net（四川省GDP网络模型），权值和阈值的训练结果如表2和表3，相对GDP的均方差函数mse为1.26091×10-5，相应的拟合精度为98.35%。

将表2、表3模型参数值代入式（2）可得具体的SCGDP-net数学表达式，或式（2）和表2、表3一起构成了SCGDPnet预测模型，其简捷、实用的表达式为：

公式中，sum（）是MATLAB的仿真函数；SCGDPnet表示训l练好的网络对象，网络结构、模型属性等所有参数都储存在其中；MG5、G6和RT6分别表示前5年的GDP均值、第6年的GDP和相对时间；54185.4等于GDP最大值的1.8倍。有了式（3），并调入MATLAB的工作空间，输入MG5和RT6的取值，就可求出第6年的GDP的预测值G6。例如，前5年（2011-2015）的GDP均值MG5=25986亿元，第6年（2016）的相对时间RT6=2016-1977=39年，代入式（3），得2016年的GDP预测值G6=31 309亿元。

（二）模型精度分析

以1978～1982、1979～1983、……、2010～2014年各前5年的GDP均值MG5和1983、1984、……、201 5年各第6年的相对年份RT6作为模型输入，由模型式（3）计算1983、1984、……、201 5年各第6年的GDP预测值列如表4的GDPO列。然后将GDPO与表1中GDP实际值进行比较，按精度P的计算公式：

P=（1-abs（GDP-GDPO）/GDP）×100（4）

计算模型预测精度如表4精度栏。结果显示，在建模年份范围，随相对时间增加，精度有逐渐提高的趋势。全部预测年份（1983～2015）的预测精度，最低为75.16%，平均为96.00%，最高为99.99%；前3年（1983～1985）和之后每5年（1986～1990，1991～1995…2011～201 5）的平均预测精度依次为85.86，93.07，96.86，98.10，97.48，97.13，99.41（%）。

将相对GDP的理论值与实际值作图对比如图2，直观显示了预测值与实际值吻合程度很好，模型的准确度很高。

三、结论与讨论

1.文章所建的GDP预测模型，具有很高的准确度，相对GDP的均方差函数mse为1.26091 x 10-5，相应的拟合精度为98.35%；全部预测年份（1983～2015）的预测精度，最低为75.16%，平均为96.00%，最高为99.99%；随相对时间增加，精度有逐渐提高的趋势。结果充分说明，人工神经网络可作为有效的GDP预测技术。

2.人工神经网络方法是基于实例的方法，不需要考虑数学模型的内部结构，不需要假设前提条件，不需要人为地确定因子权重。建模简单，模型精度高，预测程序均在MATLAB平台上完成，MATLAB功能强大的神经网络工具箱构造了网络分析和设计的许多工具函数，程序代码书写简便，预测易于完成。

3.从预测结果看，只要保证有大量的训练样本，其预测值与实际值吻合度相当高。在预测的过程中，预测者可以通过设置最小误差以及隐层神经元的个数，方便地控制预测结果的精度。

4.前处理方法是用一个较大的数MD除以每个GDP原值；后处理方法则相反，用MD乘以模型输出值。在确定MD时，除考虑神经元函数logsig的取值范围[0，1]外，还要考虑给模型留足外推预测的空间。本文研究期望所提出的预测模型能外推预测未来1-5年的GDP，故选定HD为GDP最大值30103的1.8倍，即MD=54185.4。

[责任编辑：张东安]endprint