整体式无缝桥梁徐变效应应力折减系数的计算方法

2017-09-20唐孝东蒋茂源

黑龙江交通科技 2017年7期

关键词：徐变无缝时刻

唐孝东，陈阳，蒋茂源，丁鹏

(1.重庆交通大学土木工程学院，重庆 400074；2.中交上航局航道建设有限公司，浙江宁波 315000)

整体式无缝桥梁徐变效应应力折减系数的计算方法

唐孝东1，陈阳2，蒋茂源1，丁鹏1

(1.重庆交通大学土木工程学院，重庆 400074；2.中交上航局航道建设有限公司，浙江宁波 315000)

整体式无缝桥梁的特殊结构决定了其受力的复杂性，由温度、收缩、徐变引起的应力重分布很难确定，为探究混凝土温度、收缩、徐变对整体式无缝桥梁应力的综合影响，基于线性叠加原理，在考虑徐变对温度、收缩应力的影响情况下，通过Matlab软件进行编程计算，求得了徐变效应作用下结构的温度、收缩应力折减系数，定量地描述了徐变对温度、收缩应力的影响，给徐变影响效应的理论研究提供了新的思路，具有一定的工程实用价值，有助于整体式无缝桥梁在我国的推广。

整体式无缝桥梁；应力重分布；徐变效应；收缩应力；应力折减系数

1 折减系数理论公式推导

整体式无缝桥梁属于超静定结构，徐变、温度以及收缩等外部荷载都会引起超静定结构的位移，产生次内力，改变结构的受力状态。对整体式无缝桥梁梁端固结，总应变量不变，徐变应变量的持续增长必然会导致弹性应变量的持续降低。

徐变应变量通常用徐变系数表示，即

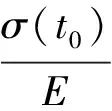
(1)

式中：εc(t,t0)表示加载龄期为t0的应力σ(t0)到计算考虑龄期t时刻的徐变应变量；εe(t0)表示t0的加载应力σ(t0)在结构上产生的瞬时弹性应变；φ(t,t0)表示徐变系数；E表示混凝土的弹性模量。

本文的计算分析需要考虑以下两点假定。

(1)将钢筋混凝土无缝桥梁结构看做素混凝土结构，忽略掉钢筋对混凝土徐变的约束作用，这是一种更不利的情况，是一种偏安全的考虑；

(2)假定结构在整个受力期间始终处于弹性阶段，其弹性模量不发生变化。

明确了计算理论及假定后，结合温度、收缩应变以及徐变系数的计算，即可得到考虑徐变与不考虑徐变的弹性应变量以及应力，进而求得应力折减系数。

1.1 不考虑徐变的应力计算

根据温度应变与温度变化的线性关系，有

(2)

式中：εT(t)表示t时刻温度应变；α为线膨胀系数；ΔT为温度增量；ΔTi为每日气温增量。

整体式无缝桥梁梁端固结，其包含温度应变、收缩应变以及弹性应变在内的总应变在任意时刻t都为零，即

ε(t)+εs(t,ts)+εT(t)=0

(3)

式中：ε(t)表示t时刻不考虑徐变的弹性应变；εs(t,ts)表示从收缩开始时的混凝土龄期到计算考虑龄期为t时间内的收缩应变。

由式(3)可得

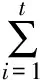
(4)

式中：σ(t)表示t时刻不考虑徐变的结构应力；(规定压应力为正，拉应力为负)

1.2 考虑徐变的应力计算

整体式无缝桥梁梁端固结，其包含温度应变、收缩应变、徐变应变以及弹性应变在内的总应变在任意时刻都为零，即

ε′(t)+εc(t)+εs(t,ts)+εT(t)=0

(5)

式中：ε′(t)表示时刻考虑徐变的弹性应变量；εc(t)表示时刻的徐变应变量；ε′(t,ts)表示t时刻考虑徐变效应的收缩应力。

由式(5)可得

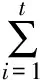
(6)

1.3 应力折减系数

根据以上的推导过程，定义t时刻考虑徐变效应下温度、收缩应力σ′(t)与不考虑徐变效应下下温度、收缩应力σ(t)之比K为应力折减系数，即

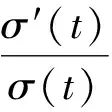
(7)

2 算例

2.1 数据

由于混凝土的徐变效应在前二十年就基本完成，本算例取计算时间t=7 200 d，以西南地区为例进行计算，根据《公路桥涵设计通用规范》(JTG D60-2004)(以下简称《通规》)，西南地区属于温热地区，对于混凝土桥梁，其有效温度标准值分别为最高气温34 ℃和最低气温-3 ℃，差值为37 ℃，年平均温度随季节的交替而缓慢变化，年温度变化的统计曲线比较接近于正弦(余弦)函数曲线，本算例将年平均温度的变化过程按照初始温度的不同分为两类，见图1、2。混凝土的膨胀系数采用α=0.000 01；取收缩开始的时间ts=7 d；西南地区环境年平均相对湿度RH=40%～60%，取RH=55%；依据《公路钢筋混凝土及预应力混凝土桥涵设计规范》(JTG_D62-2004)(以下简称《预应力设计规范》)，混凝土弹性模量取E=3.25×104MPa；构件理论厚度取h=200 mm；其余相关数据见《预应力设计规范》。

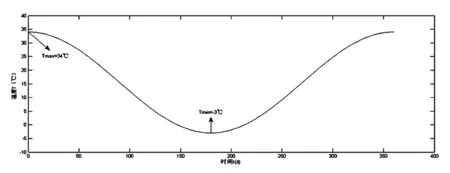
图1 年平均变化过程(1)

图2 年平均变化过程(2)

2.2 计算结果

根据初始温度的不同，分为两种情况进行计算：第一种情况考虑初始温度为最高气温，温度开始下降；第二种情况考虑初始温度为最低气温，温度开始上升。

基于上述假定、数据、编程计算方法，运用Matlab软件进行编程计算，得到两种情况下t=7 200d内、考虑徐变的温度、收缩应力随时间变化图(t-σ′(t))和不考虑徐变的温度、收缩应力随时间变化图(t-σ(t)，见图3、4。

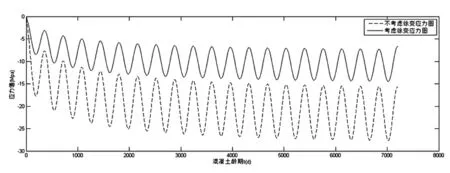
图3 考虑徐变的温度、收缩应力随时间变化图

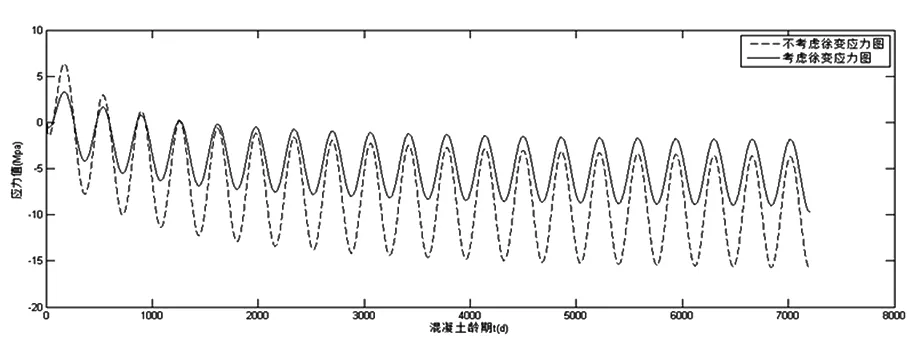
图4 不考虑徐变的温度、收缩应力随时间变化图

由图3可知，t-σ′(t)和(t-σ(t)曲线的应力值始终小于零，这是由于最开始180 d内温度的持续下降与混凝土收缩效应对结果产生相同的影响，徐变、后期的升温作用只能在一定程度上对之前的效果进行抵消，让整个结构终处于受拉状态。考虑了徐变的结构应力值始终小于没有考虑徐变的应力值，这说明徐变效应的确对混凝土的温度、收缩应力进行了折减。随着时间的发展，徐变、收缩的影响越来越弱，曲线波动的幅度趋于稳定，规律性增强。

由图4可知，t-σ′(t)和t-σ(t)曲线的应力值在初期有大于零的现象，这是由于最开始180 d内温度的持续增长对结构应力的影响处于主导地位，随着时间的增加，这种主导作用慢慢被收缩效应削弱，并最终让结构处于拉应力状态，即应力值小于零，即始终处于受拉状态。正是由于应力值在初期在正负值之间波动，两条曲线才出现了局部交叉现象，但随着时间的发展、徐变、收缩的影响越来越弱，应力逐渐在负值稳定下来，曲线的规律性也就逐渐产生了。