直线提取的预处理研究
2017-09-19顾绍通
顾绍通
(江苏师范大学 语言科学学院,江苏 徐州 221009;江苏省语言科学与神经认知工程重点实验室,江苏 徐州 221009)
直线提取的预处理研究
顾绍通
(江苏师范大学 语言科学学院,江苏 徐州 221009;江苏省语言科学与神经认知工程重点实验室,江苏 徐州 221009)
传统的直线提取算法对标准的直线比较有效,但对非典型直线并不适用。现实应用中图像由于受到噪声污染,图像中的直线会变得模糊不清,一般的直线提取方法无法提取到足够的直线信息。为了准确提取出受污染图像中足够的直线信息,以车牌和甲骨拓片字形为例,提出了一种结合分形几何与霍夫变换来提取非典型直线的方法。该方法采用基于分形几何的方法对非典型直线进行计算机辅助复原,通过计算非典型直线边缘的分形维数,对其边缘进行压缩变换,平滑非典型直线边缘因污染所造成的凹凸形态,恢复非典型直线的原貌,并利用Hough变换提取其中的直线。实验结果表明,经平滑后的非典型直线中可提取更多的直线信息,分形几何与霍夫变换的组合是有效的直线提取方法。
分形几何;分形维数;霍夫变换;直线提取
1 概 述
直线提取对于数字图像中规则目标的形状分析、识别来说是一个基本且必要的前期信息提取步骤。目前已再现多种直线提取方法,如Duda等提出的基于Hough变换的方法[1],将图像中的参数曲线在参数空间中凝聚成参数峰点,得到被检测图像中曲线的参数。该方法对于随机噪声具有良好的鲁棒性,但对存储空间要求较高,并且需要较长的计算时间,应用受到限制。Burns等提出了相位编组的方法[2],根据相位一致原理,通过直线覆盖区的像素点的边缘方向一致性来确定直线,利用了边缘方向作为低层特征,是一种比较稳定的直线提取算法;但是该方法受噪声影响大,初步得到的直线图往往存在缺损和偏差,存在丢失弱线、丢失模糊线等问题。为此,可以采用一些直线提取的后处理方法,主要有基于Bayesian框架的方法[3]、动态规划方法[4]、最小熵方法[5]。Boldt等提出了层次编组的方法[6],该方法根据共线性、邻近性、对比度相似性等先验给定的规则,将短线连成长线,但先验规则由若干人为设定的参数确定,因此该方法操作性欠佳,对图像的普适性不强。Jeong-Hun等提出了矢量基元组合的方法[7],该方法基于图像像素点的特定关系获得矢量基元,通过合并基元得出完整直线,其对基元断裂和噪声敏感,不具有鲁棒性和全局性。梅小明等提出了Beamlet变换的方法[8],通过对图像按二进、递归进行划分,利用灰度信息,积分计算每一小块图像中的Beamlets,结合梯度信息,通过广义似然比检验来检测判断符合条件假设的Beamlets,从而重建目标直线。该算法可以克服图像中的干扰及噪声,但是计算量较大,运算速度无法保证。侯彪等提出了脊波(ridgelet)变换的方法[9],该方法利用脊波框架和剖分方法实现直线特性的识别。杨波等提出了数学形态学的方法[10]。陆军等提出了基于尺度空间[11]的方法,但是该方法尺度空间直线抽取计算量较大。文贡坚等[12]采用卡尔曼滤波器跟踪衩检测图像的边缘点,得到直线支持区,然后拟合直线支持区,进而获取直线。戴激光等[13]利用高斯滤波模型进行图像去噪,然后进行边缘检测,在边缘影像上进行Hough变换,通过端点检测的方法获取直线。
以上的直线提取算法都是针对典型的直线,对于那些具有锯齿边缘,但是从整体上看呈现直线特征的非典型直线则无能为力。比如交通监控视频中提取到的车辆牌照,由于受到灯光、分辨率等因素的影响,车辆牌照会出现锯齿状边缘,但是从整体上仍然能够分清图像的大致边缘。受到污染的图像给提取直线带来了不利影响。另外,在如金文、甲骨文中,也需要对字形中的直线笔划加以提取。甲骨文是契刻在龟和兽骨上的文字,其书写材料甲骨已在地下埋藏上千年的时间,由于受到污损和发掘毁坏,导致甲骨损坏严重,拓片上有许多噪声点,字形的边缘已经非常模糊,呈现出非常明显的锯齿形态,但从整体上来看,直笔仍然具有明显的直线特征。由于字形边缘已经变得非常模糊,提取其中的直线效果很不理想。由于受到污染,非典型直线边缘呈现出连绵起伏的锯齿形状。对于这类微观上呈现锯齿边缘整体上呈现直线特征的图像来说,传统的直线提取方法已经无能为力,如何提取这类非典型直线也是一个需要加以关注的问题。
针对非典型直线的特点,采用基于分形几何的方法对非典型直线进行计算机辅助复原,计算图像边缘的分形维数,对其边缘进行压缩和变换,使得因污染所造成的凹凸形态得到平滑处理,恢复非典型直线的原貌,并利用Hough变换提取其中的直线。
2 基于分形几何的非典型直线分形变换
2.1分形几何理论
分形是关于自相似性的一般概念,由Mandelbrot[14]提出,用于描述具有相似结构的几何形状。假设有n维欧氏空间中的有界集合A,如果A能够表示为其自身Nr个互不覆盖的子集的并时,则称A是自相似的。此时,A的分形维数D定义为:
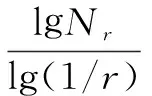
(1)
其中,r为所有坐标方向上的尺度因子;Nr为有界集合A的互不覆盖的子集个数。
对于二维图像,可以视作三维空间中的表面(x,y,f(x,y)),f(x,y)为图像(x,y)位置处的灰度值,这样,图像灰度的变化就反映在该表面的粗糙程度上,通过使用不同的尺度去度量该表面f(x,y),所得到的维数就是该图像的分形维数。估计分形维数[7]的方法有很多,其中差分盒维数法因计算简单、性能较好而应用广泛。
差分盒维数法的原理是:将m×n的图像划分成s×s的很多子块(s是1~m/2之间的整数)。假设r=s/m,图像为三维空间中的平面(x,y,f(x,y)),其中(x,y)表示点的平面位置,第三维表示像素点的灰度值f(x,y)。平面划分成众多s×s的子网格,每个网格上分布一列s×s×s的小盒子。假设图像第(i,j)个网格内灰度的最低值和最高值分别落在第k个和第l个盒内,那么Nr在第(i,j)个网格内的分布为:
nr(i,j)=l-k+1
(2)
其中,nr(i,j)为覆盖第(i,j)网格中的图像所需的盒子数,则覆盖整个图像所需的盒子数Nr为:
(3)
对于不同的r,可得不同的Nr,运用最小二乘法可拟合出lgNr~lg(1/r)的斜率,从而得到对应的分形维数D。
2.2非典型直线的分形特征
车辆牌照是交通视频监控系统中的重要信息,如何准确提取和识别车辆牌照中的直线对于提取车辆牌照中的数字至关重要。由于受到光线、分辨率等因素的影响,使得获取的车辆牌照图像中存在噪声,造成车辆牌照图像边缘产生弯曲和锯齿形态,如图1所示。

图1 车牌图像
从图1可以看出,图像中的车辆牌照比较模糊,已无法准确分辨出车辆牌照的边缘,本来是直线的牌照边缘已变得模糊,呈现锯齿形态的分形特征。
出土文献中的字形由于受到腐蚀,字形中的直线笔划已经失去原貌,呈现锯齿形态。例如,甲骨拓片字形是以出土甲骨为原型而得到的字形,因为甲骨已在地下埋藏了上千年的时间,受到了腐蚀和发掘损坏,甲骨拓片上产生很多噪声点,字形的边缘已经非常模糊,呈现出非常明显的锯齿形态,如图2所示。

图2 甲骨拓片上的字形
从图2可以看出,甲骨字形边缘已经出现锯齿形态,已不具备甲骨文字形的原貌。
图1、2中直线边缘呈现锯齿形状,这些锯齿形状边缘具有自相似性,具备分形的特征,因而可以采用分形几何加以刻画和描写。
2.3分形变换
非典型直线的边缘可以通过分形压缩变换进行平滑,从而改善非典型直线图像边缘的锯齿形状。在平面几何中,伸缩变换可以表示为:
(4)
其中,r表示伸缩比,当r小于1时为压缩变换,r大于1时为伸长变换。
非典型直线的边缘形式多种多样,可分作不同的弧线段。对于不同的弧线段分别进行变换处理。通过对各个折线段进行压缩变换,可以对非典型直线的边缘进行平滑。对弧线段进行压缩变换,首先要找到弧线段的位置。非典型直线边缘弯曲角度比较剧烈的地方,称为特征点,通过特征点可以计算弧线段的端点,从而找到每一个弧线段的位置。
特征点的提取如下所示:
θ=arc cos(V1·V2/|V1||V2|)
(5)
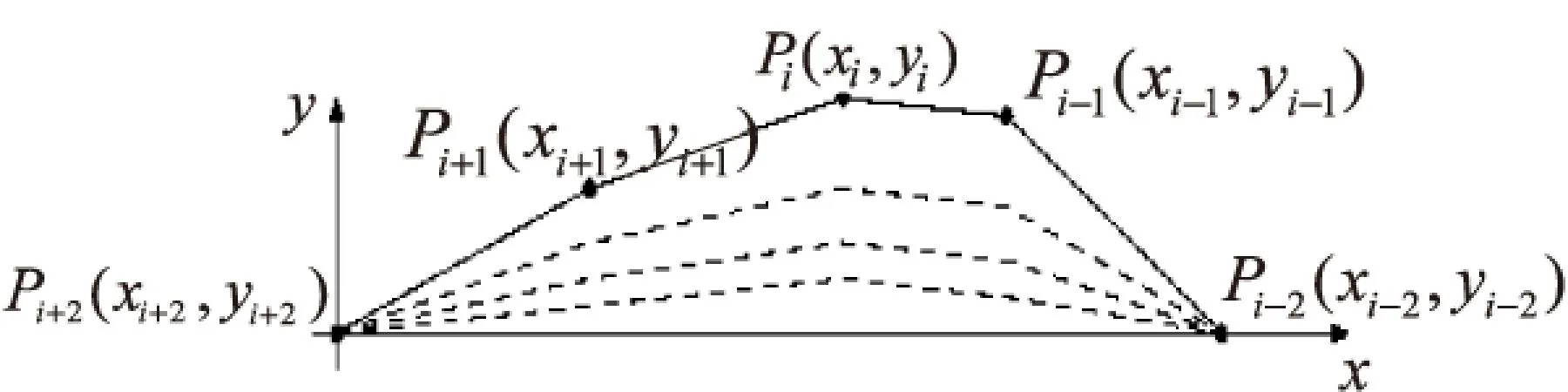
其中,θ(θ≤π)为字形轮廓上的点Pi与相邻点Pi-1、Pi+1形成的向量V1、V2间的夹角。
考虑到用户的不同需求,设计了交互功能,用户可设置不同的角度阈值。当向量夹角θ 以弧线段的首尾两个端点的连线建立X轴,过其中一点垂直于端点连线建立Y轴,建立平面直角坐标系。对弧线段进行变换时,为了既平滑对非典型直线的边缘,又保持非典型直线的基本走向和基本形状,可以对特征点及相邻特征点的坐标进行加权处理,表示如下: (6) 变换操作如图3所示。 图3 非典型直线变换处理示意图 在变换过程中,可设定分形维数的阈值,若变换后的图像分形维数小于此阈值,则变换处理结束。 算法步骤如下: Step1:采用freeman链码跟踪图像f(x,y)的轮廓; Step2:在y方向上对f(x,y)进行压缩变换,得到图像f'(x,y); Step3:计算f'(x,y)的分形维数D,如果D 该方法的优点在于抗干扰能力强。原理如下: (1)对原始图像进行二值化处理; (2)在参数空间ρ、θ建立累加数组N(ρ,θ),数组N中元素初始值为零。对于图像中以1表示的点(x,y),让θ遍历θ轴上所有可能的值,并计算对应的ρ值。根据ρ和θ的值对数组进行累加(N(ρ,θ)=N(ρ,θ)+1); (3)对N(ρ,θ)进行局部峰值检测,得到ρ和θ。 Hough变换对图像中的噪声不敏感,能够较好地处理局部遮挡、覆盖等情况。 提取非典型直线的步骤如下: (1)提取非典型直线的特征点和端点,找到折线段; (2)以折线段的首尾两个端点的连线建立X轴,过其中一点垂直于端点连线建立Y轴,建立平面直角坐标系,对轮廓上的弧线段进行加权压缩变换; (3)利用Hough变换提取直线。 在Windows环境下,在2.20 GHz CPU的计算机上,使用Visual C++6.0集成开发环境和C语言实现了上述算法。图4、图5显示了分形变换前后提取的直线信息。 图4 分形变换前后提取的直线段(1) 图5 分形变换前后提取的直线段(2) 从图中可以看出,对未经分形变换的图像提取的直线,由于图像边缘弯曲比较明显,即边缘的分形维数高,因而提取的直线信息较少。而对经分形变换后的图像提取的直线信息较多。从实验结果可得,非典型直线经过分形变换后,边缘已被平滑,提取出了更多的直线信息。 为了尽可能多地提取受污染图像中的直线信息,提出了结合分形几何与霍夫变换来提取非典型直线的方法。采用基于分形几何的方法对非典型直线进行计算机辅助复原。通过计算图像边缘的分形维数,进行加权的压缩变换处理,使得锯齿状边缘得到平滑,恢复非典型直线的原貌,然后利用Hough变换提取直线。实验结果表明,平滑后的非典型直线图像中提取到了更多的直线信息。由此可见,该方法对于那些具有锯齿边缘且从整体上看呈现直线特征的非典型直线具有明显的提取效果。 [1] Duda R, Hart P. Use of the Hough transformation to detect lines and curves in the pictures[J].Communications of the ACM,1972,15(1):11-15. [2] Burns J B, Hanson A R, Riseman E M.Extracting straight lines[J].IEEE Transactions on Pattern Analysis & Machine Intelligence,1986,8(4):425-455. [3] Tupin F,Maitre H,Mangin J F.Detection of linear features in SAR images:application to road network extraction[J].IEEE Transactions on Geoscience & Remote Sensing,1998,36(2):434-453. [4] Merlet N,Zerubia J.New prospects in line detection by dynamic programming[J].IEEE Transactions on Pattern Analysis & Machine Intelligence,1996,18(4):426-431. [5] Geman D, Jedynak B. An active resting model for tracking roads in satellite images[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,1996,18(1):1-14. [6] Boldt M,Weiss R S.Token-based extraction of straight lines[J].IEEE Transactions on SMC,1989,19(6):1581-1594. [7] Jang J H,Hong K S.Fast line segment grouping method for finding globally more favorable line segments[J].Pattern Recognition,2002,35(10):2235-2247. [8] 梅小明,张良培,李平湘.利用Beamlet变换算法提取遥感图像直线[J].计算机科学,2007,34(12):230-232. [9] 侯 彪,刘 芳,焦李成.基于脊波变换的直线特征检测[J].中国科学:E辑,2003,33(1):65-73. [10] 杨 波,汪同庆,吕永平,等.利用动态结构元素提取直线[J].计算机辅助设计与图形学学报,2003,15(4):421-424. [11] 陆 军,王润生.一种基于尺度空间理论的直线抽取算法[J].中国图象图形学报,2000,5(8):693-698. [12] 文贡坚,王润生.一种稳健的直线提取算法[J].软件学报,2001,12(11):1660-1666. [13] 戴激光,宋伟东,李建军.一种有效的直线提取算法[J].测绘通报,2012(11):59-61. [14] Mandelbrot B B.Fractals:form,chance and dimension[M].San Francisco:W. H. Freeman & Co.,1977. Investigation on Preprocessing of Line Extraction GU Shao-tong (School of Linguistic Science,Jiangsu Normal University,Xuzhou 221009,China;Key Lab of Linguistic Sciences and Neuro-cognition Engineering of Jiangsu Province,Xuzhou 221009,China) Although traditional line extraction algorithms are effective for standard lines,they are not applicable to atypical lines.The lines in image are blurry since there is noise in many applications,and sufficient information cannot be acquired with the general method of line extraction.To extract sufficient line information in noised image accurately,a method for extracting atypical lines by combining fractal geometry and Hough transform has been proposed,with car plate and Oracle character shape as the examples.It adopts the approach based on fractal geometry to realize computer-assisted restoration for atypical lines.After computation of fractal dimensions of atypical lines edges,compressing and transforming of their edges,the shape of concaves or convexes for atypical lines since noise is smoothed and their original shape are restored,extraction of straight lines by Hough transform.The experimental results show that more information has been extracted from the smoothed atypical lines and that the method of fractal geometry with Hough transform is effective. fractal geometry;fractal dimension;Hough transform;line extraction 2016-05-13 :2016-08-24 < class="emphasis_bold">网络出版时间 时间:2017-07-05 国家社会科学基金(13CYY039);教育部社会科学基金(10YJC740032) 顾绍通(1978-),男,硕士,讲师,研究方向为中文信息处理。 http://kns.cnki.net/kcms/detail/61.1450.TP.20170705.1649.010.html TP391 :A :1673-629X(2017)09-0040-04 10.3969/j.issn.1673-629X.2017.09.009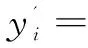
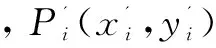
3 Hough变换的直线提取方法
4 实验及分析


5 结束语
