基于泛化能力的K-均值最佳聚类数确定方法

张 雄，赵礼峰

(南京邮电大学 理学院，江苏 南京 210023)

基于泛化能力的K-均值最佳聚类数确定方法

张 雄，赵礼峰

(南京邮电大学 理学院，江苏 南京 210023)

针对K-均值聚类算法需要事先确定聚类数，而人为设定聚类数存在极大主观性的缺点，提出了一种基于泛化能力的最佳聚类数确定方法。该方法认为：一个好的聚类结果，应该对未知的样本有着良好的泛化能力。其通过设计一种泛化能力指标(GA)来评价得到的聚类模型对未知样本的分类能力，泛化能力指标的值越大，则聚类模型的效果越好，以泛化能力最优的聚类模型所对应的K值作为最佳聚类数。为了测试所提出方法的稳定性和有效性，分别基于真实数据集Iris以及人造数据集对基于泛化能力的最佳聚类数确定方法进行了实验验证，均能准确找到数据集最佳聚类数。实验结果表明，该方法能够简单、高效地获得最佳聚类数，且对数据集的聚类效果良好。

K-均值；最佳聚类数；泛化能力；非监督学习

0 引 言

聚类分析[1]也称无教师学习或无指导学习，它是在没有训练目标的情况下将样本划分为若干簇的方法，其目的是建立一种归类方法，将一批样本或变量，按照它们在特征上的疏密程度进行分类，使得组内样品的相似度达到最大，而组间的差异也达到最大。到目前为止，还没有一种具体的聚类算法可以适用于解释各种不同类型数据组成的多样化结构数据集。聚类方法大致可分为以下几种：划分式聚类算法、层次聚类算法、基于密度的聚类算法、基于网格的聚类算法和基于模型的聚类算法[2]。其中，K-均值聚类[3]是划分式聚类算法中最常用的算法之一，近年来，许多学者对它进行了研究和改进，使得K-均值聚类算法逐渐形成了一个较为完善的聚类体系。但是，K-均值算法依然存在缺点：无法事先确定聚类数目。不根据数据本身来确定k值的主观性较强，由于缺乏数据支持，从而导致聚类的效果不佳。

为了更加科学地确定聚类数，从而减小聚类数的选取对聚类效果的影响，周世兵等[4]提出了一种新的聚类有效性指标—BWP指标。该指标通过计算聚类结果中某一个样本点的最小类间距离与类内距离之和比上最小类间距离与类内距离之差，从而反映出聚类结构的类内紧密性和类间分离性，根据BWP指标的大小来选取最佳聚类数。李芳等[5]提出了一种针对大数据集的K-均值改进算法，将最小生成树算法应用在初始的k个聚类中心，通过合并相似度最大的聚类中心以减小k值，直到评判函数收敛，最终得到较优聚类数的聚类结果。李龙龙等[6]提出了一种新型模糊半监督加权聚类算法，采用4种模糊聚类有效性评价算法依次对不同聚类数下的聚类结果进行分析，最终通过不同聚类评价结果的对比分析得到实验数据的最佳聚类数。

但是，目前对于K-均值聚类算法的改进[7-12]大多是基于聚类分析中的最大最小距离，即认为一个好的聚类结果应该尽可能地反映数据集的内在结构，使得类内距离尽可能小，类间距离尽可能大。但是，这种基于聚类结构方法的缺点也很明显，由于需要计算每个样本点之间的距离，在处理高维海量数据时，计算量太大，导致效率低下。

针对上述问题，从不同于聚类结构的另一个角度(泛化能力)来对聚类结果的有效性进行评价。基于有指导学习的思想，亦即一个好的聚类结果，还应能对未知的样品进行预测，并且预测结果与未知样品自身的聚类可以做到很好的拟合，这种对未知样品的类别进行准确预测的能力被称为聚类结果的泛化能力。在此基础上，提出了一种最佳聚类数确定方法。

1 相关知识

1.1K-均值聚类算法

K-均值算法是一种典型的划分聚类方法，其思想是在给定聚类数k时，通过最小化组内误差平方和来得到每一个样本点的分类。

算法流程如下：

(1)确定聚类数k，并从n个样本点中任意选择k个点作为初始聚类中心；

(2)计算其余点与k个聚类中心间的距离，根据距离的大小将它们分配给其最相似的中心所在的类别；

(3)采用均值法重新计算每个新类的聚类中心；

(4)不断重复步骤2和步骤3，直到所有样本点的分类不再改变或类中心不再改变。

由于不需要计算任意两个样本点之间的距离，因此K-均值聚类往往用于大规模的数据，并且比其他聚类方法的收敛速度更快。然而，K-均值聚类容易受到初始聚类中心的影响，不适用于非凸的数据集；其次，聚类数的确定也是聚类分析中一个非常重要的问题，它对聚类的有效性和聚类结果的解释都有直接的影响；另外，在高维数据集的聚类中，聚类变量的选择也是一个重要的问题，维数过高会使空间中的点变得稀疏，从而使距离失效。

1.2最佳聚类数确定方法

传统的聚类数确定，是通过聚类有效性指标来评价不同k值下聚类结果的优劣，从而选出最优的聚类数。

常用的聚类有效性指标[13]包括Calinski-Harabasz(CH)、Davies-Bouldin(DB)、Weighted inter-intra(Wint)、Krzanowski-Lai(KL)、Hartigan(Hart)、In-Group Proportion(IGP)等。其中，IGP是基于数据集统计信息的指标，而其他指标全都是局域数据集样本集合机构的指标，他们不依赖外部的参考标准，只依据数据集本身的统计特征对聚类结果进行评估，并根据结果的优劣选取最佳聚类数。

下面对最常用的CH、DB和Wint指标进行介绍。

(1)CH指标。

CH指标通过类内离差矩阵描述紧密度，类间离差矩阵描述分离度，指标定义为：

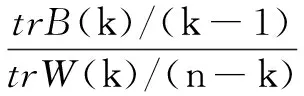
(1)

其中，n表示聚类数目；k表示当前的类；trB(k)表示类间离差矩阵的迹；trW(k)表示类内离差矩阵的迹。

可以看出，CH越大，类自身越紧密，类与类之间越分散，即得到更优的聚类结果。

(2)DB指标。

DB指标是基于样本的类内散度与各聚类中心的间距的方法，其定义为：

(2)

其中，k为聚类数目；wi为Ci类中的所有样本到聚类中心的平均距离；wj为类Cj中的所有样本到类Cj中心的平均距离；Cij为类Ci和Cj中心之间的距离。

可以看出，DB越小，表示类与类之间的相似度越低，从而对应的聚类结果越优。

(3)Wint指标。

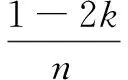
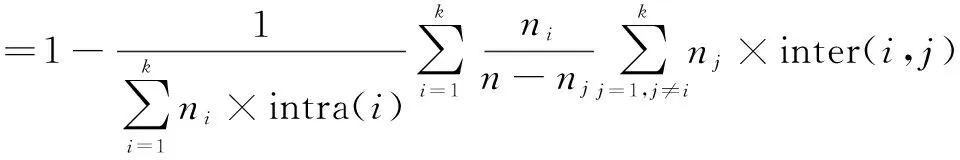
(3)

其中，intra(i)表示类内相似度；inter(i,j)表示类间相似度。

1.3泛化能力

泛化能力[14]常见于人工神经网络，是用来评价一个分类器性能的指标。所谓泛化能力，是指从训练样本数据得到的模型，能够很好地适用于测试样本数据，训练集上训练的模型在多大程度上能够对新的实例预测出正确输出称为泛化能力(Generalization Ability，GA)。

2 基于泛化能力评价指标的最佳聚类数确定方法

基于泛化能力的最佳聚类数确定方法是通过分类的思想来解决聚类问题，将无指导的聚类与有指导的学习结合起来，通过对不同k值得到的聚类结果泛化能力的比较得出最优聚类数，将聚类泛化能力的评价指标定义为GA，其公式为：

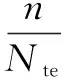
(4)

GA指标的具体计算方法如下：

(1)将给定的数据集进行随机拆分，分为训练集tr和测试集te；

(2)分别对训练集和测试集进行K-均值聚类，聚类数都为k，分别得到训练集的聚类结果tr1和测试集的聚类结果te1；

(3)应用分类方法，对步骤2中得到的tr1进行学习，并根据学习到的判别函数对测试集中的样本进行判别，判别结果为te2；

(4)比较te1和te2中对应样本的类别，计算te1和te2中类别相同的样本个数n占测试集样本总数Nte的比例，取值区间为[0，1]。

不同于传统的聚类有效性指标，GA指标不是从聚类结果的结构来评价聚类效果，而是应用人工神经网络中的泛化能力来衡量聚类的有效性，GA指数越大，说明该聚类泛化能力越高，聚类效果越佳。然而该指标不适用于聚类数为1的聚类，此时GA指数为1，虽然达到了最大，但此时的聚类本身是没有意义的。

另外，在实际聚类中，聚类数不应过多，否则对于聚类结果将难以解释，因此对于有限的可选聚类数，可以采用穷举法得到。通过计算不同聚类数下的GA指数，选择最大的GA指数对应的聚类数作为整体数据集的最佳聚类数，并对原始数据整体进行聚类，得到最优的聚类结果。

3 数值实例

利用R语言编程环境实现算法，为检测所提方法的有效性和稳定性，分别对人工数据集和真实数据集进行仿真实验。

3.1人工数据集

利用R软件生成人工数据集dataset，dataset由三个簇共900个二维点构成，该数据集数据构成如表1所示。

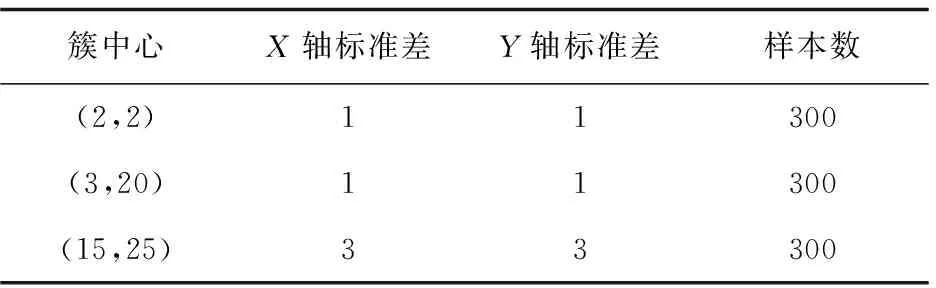
表1 dataset的数据构成

dataset的分布情况如图1所示。

图1 dataset的分布

根据GA指标的计算流程，将这900个样本随机分为两部分，一部分作为测试集，一部分作为训练集，其比例为3∶7。通过以上步骤，将数据集分为两部分，其中train为训练集，有637个样本，test为测试集，有263个样本。分别对测试集和训练集进行K-均值聚类，k值的选取采用穷举法，即k=2，3，4，5，依次进行聚类。

之后根据训练集的聚类结果对测试集进行分类，将得到的分类结果与之前的聚类结果进行对比，求出不同k值下的GA指数，结果如表2所示。

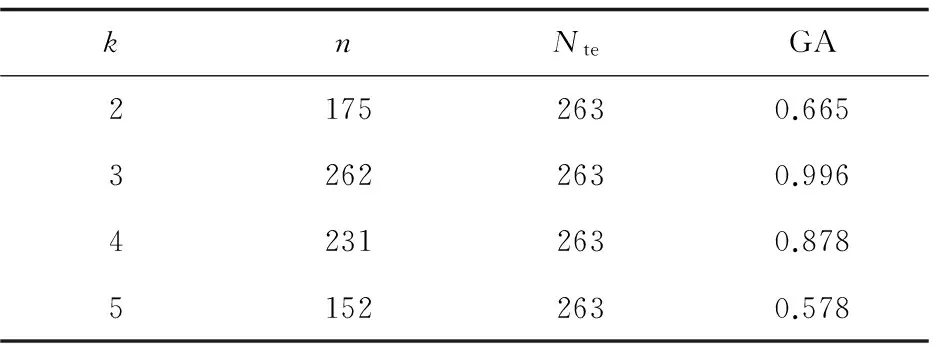
表2 不同k值下的GA指数(dataset)

通过表2可以看到，当k为3时，GA指数达到最大，因此对于dataset，最佳聚类数为3，此时聚类模型具有更强的泛化能力，是该数据集最佳的聚类模型。

接下来对dataset的所有数据进行k值为3的K-均值聚类，得到的三个聚类中心分别为：(1.86，1.98)，(3.12，20.04)，(14.84，25.37)，与生成dataset时设定的三个簇中心很接近，且所有样本点的聚类结果都与原始类别吻合，说明聚类效果很好。

3.2真实数据集

数值实例所用数据是R软件中自带的iris数据集，该数据集由不同种类鸢尾花的150个样本数据构成，每个样本有4个变量，分别为：Sepal.Length(花萼长度)、Sepal.Width(花萼宽度)、Petal.Length(花瓣长度)、Petal.Width(花瓣宽度)。通过iris数据集的四个自变量对150个样本进行聚类。接下来，对这150个样本进行基于泛化能力的聚类分析，并确定最佳聚类数。

首先，还是对iris数据集进行划分，随机选取其中的44个样本作为测试集，剩下的106个样本作为训练集，然后计算不同k值下的GA指数。k值采用穷举法，分别选取2、3、4、5，最后得到的结果如表3所示。

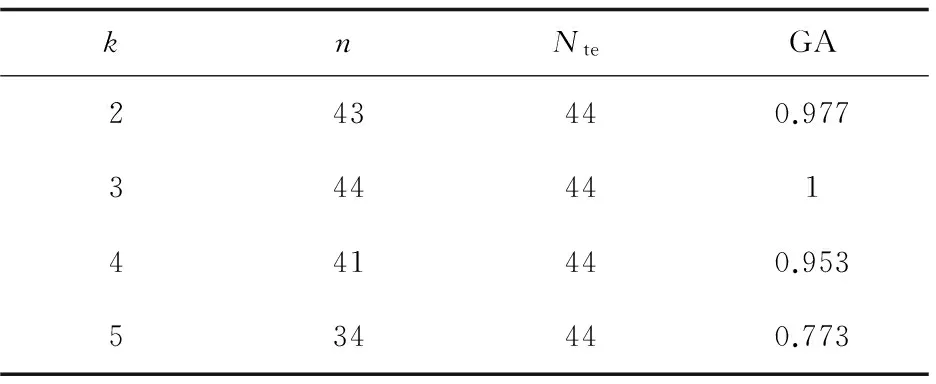
表3 不同k值下的GA指数(iris)

通过表3可以看到，当k=3时，测试集中的44个样本全都被正确地分到了三类中，GA指数达到最大1，说明此时的聚类模型泛化能力最高，聚类效果最理想，由此可以判断iris数据集的最佳聚类数为3。而当k取2，4，5时，都存在一定的误判，这样的聚类结果的泛化能力不够高，不是该数据集最优的聚类模型。

接下来对iris数据集进行k值为3的K-均值聚类，将聚类结果与原始样本所属类别进行比较，发现在所有的150个样本中，有136个样本被准确分类了。对于前两种花的分类结果比较理想，而第三种花的误判较高，后两类之间存在小范围的重叠，这可能与数据量的大小有关，过小的数据量导致聚类算法不能更加有效地学习到各类的特征，从而导致聚类结果的误判。

4 方法评价与改进

不同于现有的基于聚类结构的最佳聚类数确定方法，所提方法为最佳聚类数的确定提供了一条新的思路，同时在一定程度上解决了现有方法计算复杂效率低下的缺点，具有较好的应用价值。另外，该方法不仅仅适用于K-均值聚类，对于其他需要提前确定聚类数的聚类算法，都可以通过该方法来提前确定最佳聚类数。

但是该方法依然存在不足，即对于样本量较小的数据集，在对特征进行学习时无法更加准确地构建分类器，从而导致GA指标计算结果的精度有所降低，因此该方法更加适用于高维度的海量数据，而这恰恰是现有其他方法存在不足的地方。

5 结束语

针对K-均值算法需要人为设定k值，且现有的k值确定方法都是基于聚类模型结构这一不足，提出了一种基于泛化能力的最佳聚类数确定方法。该方法通过设计出的GA指标来对聚类模型的泛化能力进行评价，并以此作为聚类有效性的评价指标，选择GA指数最大的k值作为最佳聚类数。对人工生成数据和真实数据的两次实验结果表明，该方法可以有效地得到最佳聚类数，从而得到最优的聚类模型。

[1] 孙吉贵，刘 杰，赵连宇.聚类算法研究[J].软件学报,2008,19(1):48-61.

[2] 王 实，高 文.数据挖掘中的聚类方法[J].计算机科学,2000,27(4):42-45.

[3] 冯 超.K-means聚类算法的研究[D].大连：大连理工大学，2007.

[4] 周世兵，徐振源，唐旭清.新的K-均值算法最佳聚类数确定方法[J].计算机工程与应用，2010,46(16):27-31．

[5] 李 芳.K-means算法的k值自适应优化方法研究[D].合肥：安徽大学，2015.

[6] 李龙龙,何东健,王美丽.模糊半监督加权聚类算法的有效性评价研究[J].计算机技术与发展,2016,26(6):65-68.

[7] 张忠平，王爱杰，柴旭光.简单有效的确定聚类数目算法[J].计算机工程与应用,2009,45(15):166-168．

[8] Mehar A M,Matawie K,Maeder A.Determining an optimal value of K in K-means clustering[C]//IEEE international conference on bioinformatics and biomedicine.[s.l.]:IEEE,2013:51-55.

[9] 贾瑞玉，宋建林.基于聚类中心优化的k-means最佳聚类数确定方法[J].微电子学与计算机，2016,33(5):62-66.

[10] 王 勇，唐 靖,饶勤菲,等.高效率的K-means最佳聚类数确定算法[J].计算机应用，2014,34(5):1331-1335.

[11] 张 琳，陈 燕，汲 业,等.一种基于密度的K-means算法研究[J].计算机应用研究，2011，28(11):4071-4073．

[12] 李双虎，王铁洪.K-means聚类分析算法中一个新的确定聚类个数有效性的指标[J].河北省科学院学报，2003，20(4):199-202．

[13] 宋 媛.聚类分析中确定最佳聚类数的若干问题研究[D].延边：延边大学，2013.

[14] 魏海坤，徐嗣鑫，宋文忠.神经网络的泛化理论和泛化方法[J].自动化学报，2001,27(6)：806-815.

A Method for Determination of Optimal Value inK-means Clustering with Generalization

ZHANG Xiong，ZHAO Li-feng

(College of Science,Nanjing University of Posts and Telecommunications,Nanjing 210023,China)

Aimed at the defect ofK-means clustering algorithm determining the clustering number in advance which could be defined artificially and is subjective in computations,a method of determining an optimal clustering value with generalization is proposed.It is thought that a good clustering result should have good generalization to the unknown samples.Therefore,a generalization index is designed to evaluate the classification of the unknown samples in the clustering model obtained.The more the value of generalization index,the better the effect of clustering model.TheKvalue corresponded by clustering model with optimal generalization is selected as the optimal clustering value.In order to verify its stability and effectiveness,the experiments are carried out in optimal clustering determining methods based on generalization based on Iris and artificial data set,which indicate that it is simple and efficient to obtain the optimal clustering number,and has the good clustering effect.

K-means clustering;optimal number of clusters;generalization;unsupervised learning

2016-09-07

：2016-12-14 < class="emphasis_bold">网络出版时间

时间：2017-07-05

国家自然科学基金青年基金项目(61304169)

张 雄(1993-)，男，硕士研究生，研究方向为信息统计与数据挖掘；赵礼峰，教授，硕士生导师，研究方向为图论及其在通信中的应用。

http://kns.cnki.net/kcms/detail/61.1450.TP.20170705.1651.054.html

TP301

:A

:1673-629X(2017)09-0031-04

10.3969/j.issn.1673-629X.2017.09.007