导流孔周水平方向孔隙水压力分布规律

胡世丽，王 敏，王观石，2，洪本根，罗嗣海

(1.江西理工大学建筑与测绘工程学院，江西 赣州 341000；2.中国科学院寒区旱区环境与工程研究所，甘肃 兰州 730000；3.江西理工大学资源与环境工程学院，江西 赣州 341000)

导流孔周水平方向孔隙水压力分布规律

胡世丽1，王 敏1，王观石1，2，洪本根3，罗嗣海1

(1.江西理工大学建筑与测绘工程学院，江西 赣州 341000；2.中国科学院寒区旱区环境与工程研究所，甘肃 兰州 730000；3.江西理工大学资源与环境工程学院，江西 赣州 341000)

掌握导流孔周孔隙水压力分布规律对计算原地浸矿母液回收率具有重要意义。假设水沿水平方向流入导流孔的通道为普遍存在的2分叉分形树状网络结构，基于Hagen-Poiseuille方程，提出导流孔周水平方向孔隙水压力分布计算公式。室内模型试验结果表明，采用2分叉分形树状网络结构描述水流入导流孔的渗流通道是有效的；随初始水头增加，描述树状分叉网络的各级圆管长度比逐渐增加，且增加幅度越来越小，但是各级圆管的直径比和初级母管长度逐渐减小，并渐趋稳定，各级圆管的直径比稳定值为0.84。

导流孔；孔隙水压力分布；分形树状网络；原地浸矿

离子型稀土矿开采利用始于20世纪70年代，先后经历了池浸、堆浸和原地浸矿3种工艺技术，目前，正推广应用“原地浸矿”工艺[1-2]。“原地浸矿”工艺是综合了地质、采矿、矿物加工等多学科的集成技术，工艺推广时间较短，因而工艺本身还存在不少技术难题有待进一步解决[3]。其中，如何高效回收浸出液是“原地浸矿”工艺面临的核心技术难题之一，特别是地质条件复杂、底板裂隙发育的稀土矿体。赣南稀土矿山中70%不具备完好底板，因裂隙渗漏导致相当部分的浸出液流失，在有些矿山甚至大部分浸出液都无法回收[4]，因而收液技术直接影响“原地浸矿”工艺推广应用。

现有工程实践表明，收液效果最好的收液技术是导流孔—收液巷道组合收液技术，通常收液率能达到70%以上。该技术具体操作是：在收液巷道边壁上打垂直边壁的导流孔，每壁设置3～5 个/m，分上下两层交错布置。目前采用孔径为10 cm导流孔成孔技术，假设导流孔布置密度为5 个/m，如果溶液流入导流孔的过程为只有重力作用的渗流过程(无压力水头作用)，根据导流孔截流面积与过水断面面积比，可以计算得到导流孔收液率约为50%，小于实际收液率70%，由此说明，溶液是在重力和压力共同作用下流入导流孔。为便于表述导流孔对原地浸矿渗流场的影响，使溶液流入导流孔的重力和压力统一为水头，本文将未受导流孔影响的孔周水头称为初始水头。

导流孔周渗流规律的研究主要集中在把导流孔类比为“水平井”，通过改变渗流场的宏观边界条件，达到控制渗流场参数的目的，该方法在水利、矿业、交通等领域广泛应用，但基于分形理论从微观几何结构研究多孔介质渗流规律模型鲜有涉及[5]。大量文献报道表明，土壤、沙石、多孔材料等多孔介质具有分形特征，并且已有学者基于分形几何概念及多孔介质微观特性对多孔介质渗透输运性质进行了一定的研究，也有学者利用分形树状分叉网络结构模拟各向异性多孔介质中水力分叉和裂缝网络，建立各向异性多孔介质径向渗流微几何模型[6]。矿体中的水向导流孔或收液巷道汇集过程复杂多变，但分形理论能对此复杂现象精确描述，距导流孔或收液巷道越近，流速越大，该渗流规律利用分形树状分叉网络结构可以准确模拟。

本文运用分形理论，假设水沿水平方向流入导流孔的通道为普遍存在的2分叉分形树状网络结构，建立导流孔周水平方向孔隙水压力分布的分形计算方法，并通过室内模型试验，研究不同初始水头条件下单个导流孔周孔隙水压力变化规律。

1 导流孔周水平方向孔隙水压力分布计算方法

1.1分形树状分叉网络理论基础

如图1所示，单个树状分叉网络由初级母管(第0级)到末级第m级按照Y分叉规则生产，分叉角为2θ，分叉数为n，图1中n=2。设dk和lk表示第k(k=0，1，2…，m)级分叉管道的直径和长度，dk+1和lk+1表示第k+1级分叉管道的直径和长度，定义αk、βk为相邻两级分叉管道的长度比和直径比分别见式(1)、式(2)。

(1)

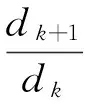
(2)

若单个树状分叉网络结构满足分形特征，则长度比和直径比必须保持常数[7-8]，即：αk=α，βk=β，n=2，θ=300。

图1 单个树状分叉网络结构图

水在流入导流孔的过程中，越靠近导流孔孔壁，流速越大，导致树状分叉结构也具有非均匀性。假设水沿水平方向流入导流孔的通道为普遍存在的2分叉分形树状网络结构，分布在导流孔孔壁处的圆管为初级母管(第0级)，若保证整个渗流区树状分叉结构满足分形要求，则初级母管直径分布满足分形标度[9-10]，由文献[11]可得分布在导流孔孔壁处的初级母管直径满足式(3)。

(3)

其中：dmin和dmax是初级母管的最小和最大直径；Dρ为初级母管直径分形维数。

式(3)是判断多孔介质满足分形的依据，但自然界中很少有绝对满足式(3)的分形系统。对多孔介质而言，若dmin/dmax≤10-2[12]，则说明多孔介质满足分形要求。由文献[13]可知离子型稀土矿孔径分布满足dmin/dmax<10-2即满足分形分布。

1.2导流孔周水平方向孔隙水压力分布表达式

假设水经分形树状分叉网络流入导流孔为不可压缩的稳定径向层流，不同分叉结构相同级别的分叉管道压差相等，通过任意级别处流量相等，由修正的Hagen-Poiseuille方程，可得第k级和第k+1级单管流量表达式分别见式(4)和式(5)。

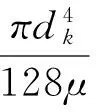
(4)

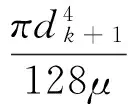
(5)

其中：qk和qk+1分别为第k级和第k+1级单管流量；μ是流体粘滞系数；Δpk和Δpk+1分别为第k级和第k+1级压力差。

由单分叉第k级圆管总数nk，第k+1级圆管总数nk+1，根据流量守恒原则可得第k+1级单个圆管流量qk+1与第k级单个圆管流量qk之比，见式(6)。

(6)

根据式(1)、式(2)及式(4)、式(5)代入式(6)，可得第k+1级压差Δpk+1和第k级压差Δpk之比，见式(7)。整个渗流区域的总压差Δp可表示为式(8)。由式(8)可得出初级压差Δp0，见式(9)。

(7)

(8)

(9)

若pk表示第k级分形树状分叉网络末端的孔隙水压力，则pk(k=0，1，2…m)可以表示为式(10)。

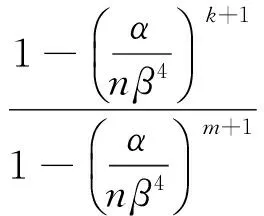
(10)

由图1可以确定距导流孔等效水平直线距离r，见式(11)。

(11)

式中：rw为导流孔半径。

利用式(11)求解出分叉级数k，当等效直线距离r取影响范围rm时，求解出总分叉级数m，将k和m带入式(10)，建立导流孔周水平方向孔隙水压力分布，得式(12)。

(12)

式中，pr为距导流孔直线距离r处的孔隙水压力。

通过室内模型试验，获得导流孔周水平向孔隙水压力分布曲线，并运用式(12)拟合，确定不同初始水头作用下导流孔周水平方向孔隙水压力分布参数α、β、l0。

2 导流孔周水平方向孔隙水压力分布测试

2.1试验装置

试验装置如图2所示，主要由注液装置、箱体、孔隙水压力采集系统、导流孔、渗漏底板和集液空间共5部分组成。

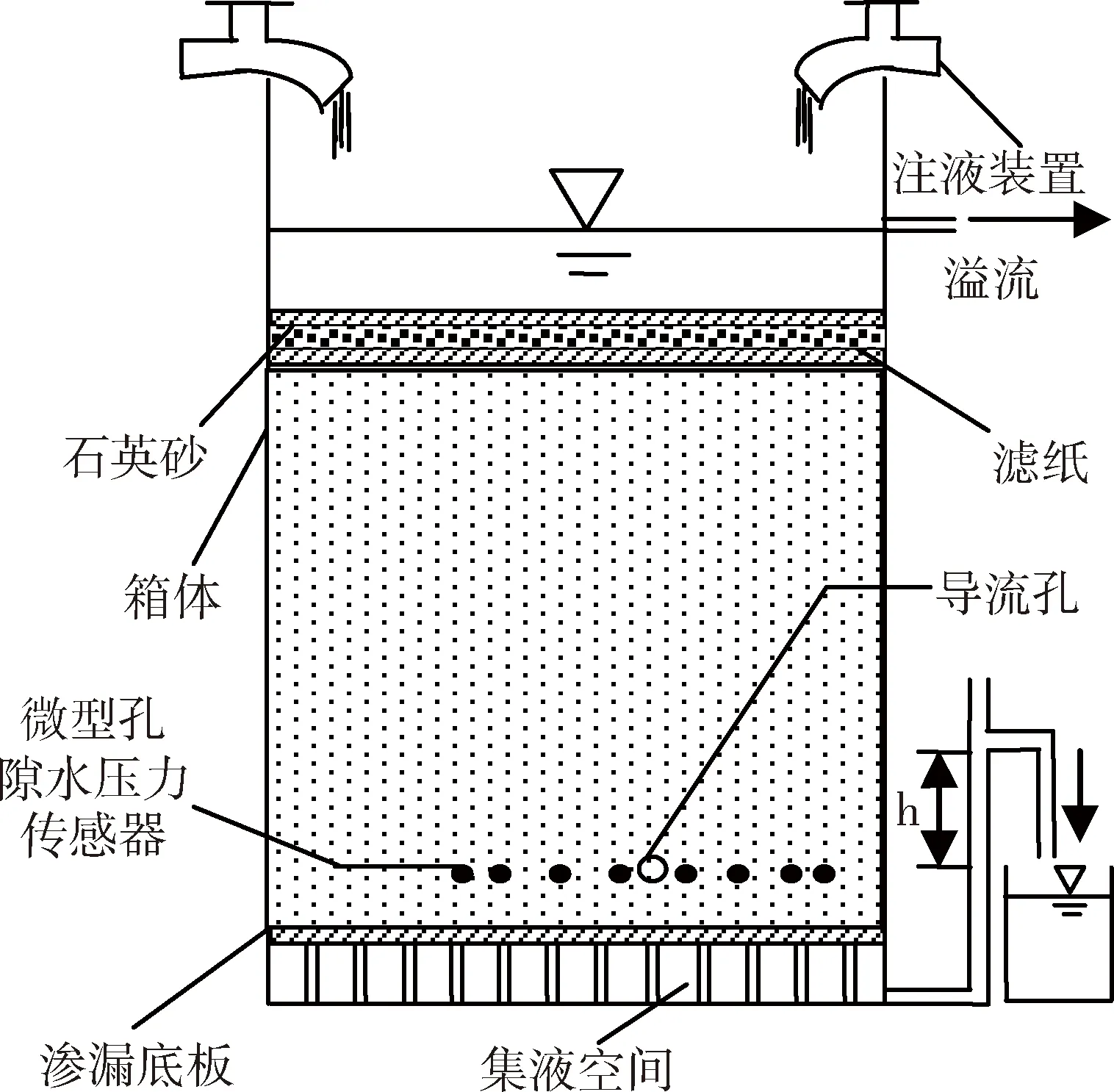
图2 试验装置示意图

2.1.1 注液装置

试验注入液体为清水，采用注液桶注液，注液桶标有刻度，量程为58 L，注液桶底部装有水龙头，以便调节注液强度。

2.1.2 箱体

箱体为长方体，长×宽×高=1.0 m×0.5 m×1.1 m，用来装填试验矿样，上部敞开，便于观测和调整试验矿样上部水头，箱体右上侧距离试验矿样5 cm高处开一小孔，试验过程中，矿样上方多余清水从小孔排出，维持矿样上方水头恒定，为防止箱体变形，水沿箱体壁向下渗流，采用1 cm厚的不锈钢制成箱体。

2.1.3 孔隙水压力采集系统

孔隙水压力采集系统包括微型孔隙水压力传感器、采集卡和计算机，采集卡一端与微型孔隙水压力传感器相接，另一端通过USB装换器与电脑相接，结合与之配套的数据采集软件，实现数据的读取和存储。微型孔隙水压力传感器(型号：CYY2，量程—10 k～+10 kPa，精度±0.25%)距渗漏底板高度10 cm，共埋置8个，从左向右依次编号1#～8#，1#～4#布置在导流孔左侧，距导流孔分别为35 cm、25 cm、15 cm、5 cm，5#～8#布置在导流孔右侧，距导流孔分别为5 cm、15 cm、25 cm、30 cm。试验过程中，动态采集孔隙水压力的变化过程。

2.1.4 导流孔

在箱体正面开1个孔作为导流孔出口，该孔距箱体左侧壁60 cm，右侧壁40 cm，距渗漏底板10 cm，导流孔采用直径2 cm，长40 cm的不锈钢钢管，上半部均匀开一系列小孔，小孔直径2 mm，孔间距1 mm，收液孔出口端与球阀连接，末端密封，保证溶液只能从管壁上半部流入，外壁覆盖一层滤纸，防止细颗粒阻塞小孔，影响水流入导流孔。

2.1.5 渗漏底板和集液空间

在试验矿样底部，按照从上向下依次布置滤纸、尼龙布和含有大量小孔的钢板，这就组成了渗漏底板，在渗漏底板下部设置集液空间，高度8 cm，水通过渗漏底板汇集到集液空间，流向箱体右侧壁阀门，在阀门出口端连接可调高度的软管，通过改变远处软管水头高度h来改变导流孔周水平方向孔隙水压力分布，本文将水头h称为初始水头。

2.2试验矿样制备与装填

取江西赣南某矿区离子型稀土矿风干样，测其初始含水率为1.39%，配制高1.0 m、孔隙比0.95和含水率18%的试验矿样，分10层依次均匀填装夯实，为避免出现矿层分界面，两层交界处的矿样表面作刨毛处理，最上层矿样上部铺设一层3 cm厚石英砂并覆盖一层滤纸作缓冲层。防止注液时顶部矿样被冲刷，同时保证入渗均匀。装填过程中按设计要求埋设微型孔隙水压力传感器和导流孔，装填好矿样后开始记录微型孔隙水压力传感器读数，待各微型孔隙水压力传感器读数稳定一段时间后开始注清水。

2.3试验过程

1)仪器检查。检查各微型孔隙水压力传感器乳胶管内是否有气泡、漏水，接线是否良好，供电系统能否正常供电，各微型孔隙水压力传感器和采集系统能否正常运行。

2)试验矿样饱和。打开导流孔及箱体右侧壁阀门，加水直到溢水口有水流出，此时打开注液装置对矿样注清水，每隔一段时间，记录注液量Q1、总收液量(导流孔收液量和底板渗漏量)Q2以及微型孔隙水压力传感器测量值，待注液量、总收液量以及各微型孔隙水压力传感器测量值稳定后，并计算得到矿样饱和度大于80.0%，认为矿样饱和[14]。

3)正式实验。以上述稳定渗流状态为初始条件，将初始水头设定为h1=31 cm，调节注液量，直到溢水口刚好有水溢出，记录注液量Q1、总收液量Q2(导流孔收液量和底板渗漏量)以及相应位置处微型孔隙水压力值，待注液量、收液量以及各微型孔隙水压力传感器测量值稳定即渗流稳定后，结束本组试验。之后分别将初始水头设定为h2=36 cm、h3=50 cm、h4=62 cm和h5=77 cm，重复上述试验操作，直至所有试验完成。

3 导流孔周水平方向孔隙水压力分析

3.1导流孔周水平方向孔隙水压力分布拟合

如果想采用数据拟合方法确定参数α、β、l0，并减小拟合误差，需要尽可能多的试验数据，即尽可能多布置微型孔隙水压力传感器。由于微型孔隙水压力传感器具有一定体积，如果增加传感器埋设数量，传感器本身对流场的影响进一步突显。为此，本文采用三次幂函数，通过数据拟合确定导流孔周孔隙水压力在水平方向上的变化规律。以初始水头h2=36 cm为例说明拟合过程，当渗流稳定后，距导流孔的距离大于22 cm，孔隙水压力值随径向距离增加变化很小，由文献[15]可将单个导流孔的影响范围rm取值为22 cm，采用三次幂函数拟合得到水平方向上孔隙水压力与径向距离关系，如图3所示。

采用相同的方法，拟合得到5种初始水头作用下孔周水平方向孔隙水压力变化规律，如图4所示。由图4可知，在不同初始水头h作用下，导流孔周孔隙水压力大致呈对称状的降落漏斗，靠近导流孔水压力值较低，远离导流孔水压力值较高，离导流孔越近水压力值下降越快，远离导流孔，水压力值下降速度越来越慢，渐趋稳定[16]。这是因为水向导流孔运动过程中，越靠近导流孔流速越大，压力损失越快，水压力值也就越低。

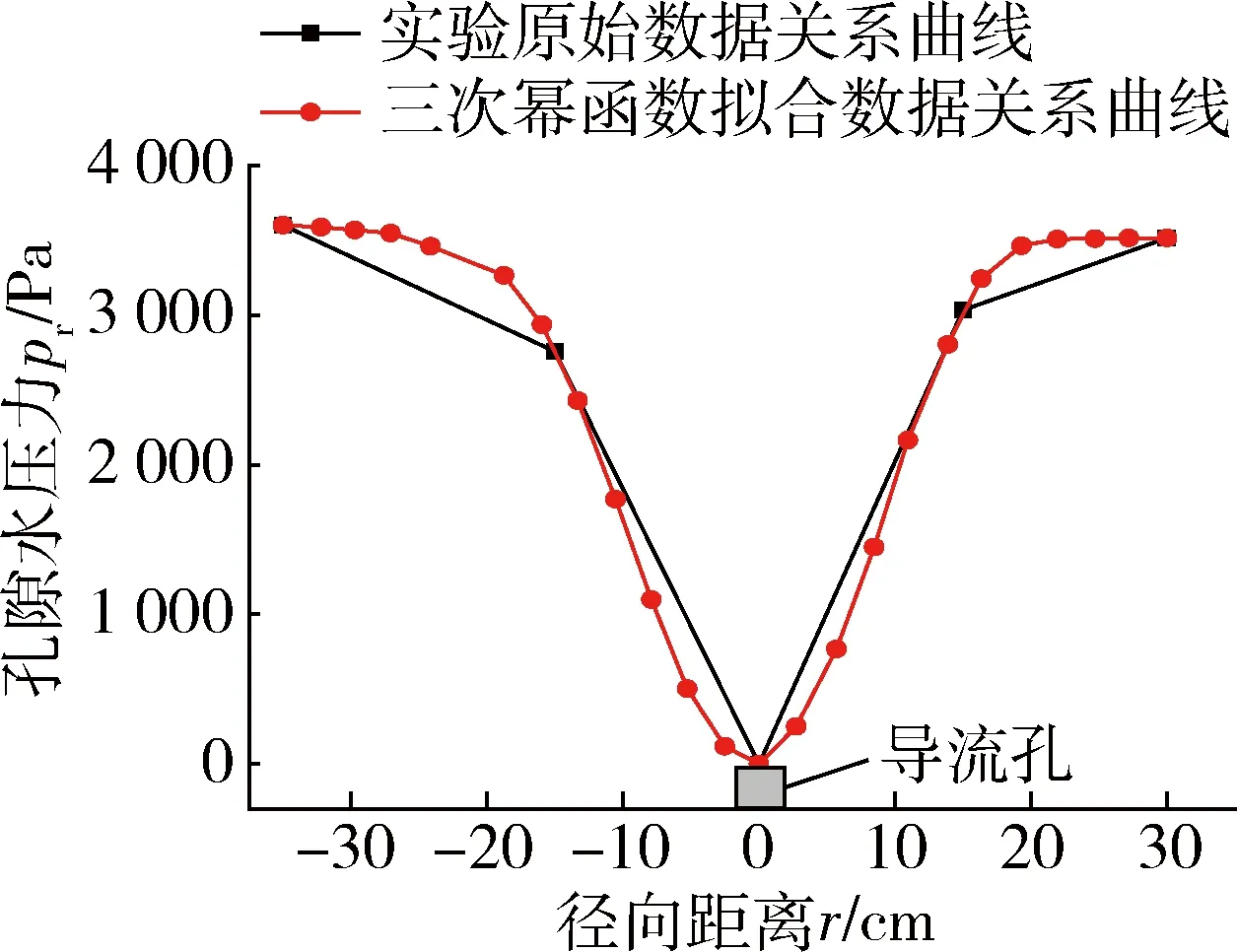
图3 导流孔周水平向孔隙水压力拟合

图4 导流孔周水平方向孔隙水压力分布

3.2导流孔周水平方向孔隙水压力分形参数计算

以初始水头h2=36 cm为例，导流孔周水平方向孔隙水压力分形参数计算，采用最小二乘法，运用式(12)拟合得到导流孔左右两侧水平方向孔隙水压力分形参数，拟合结果如图5所示。图5表明，两种拟合结果非常接近，平均误差小于10%。

采用相同的方法拟合得到三个分形参数与初始水头关系，如图6～8所示。图6表明，初始水头h由31 cm增至77 cm，右侧长度比由0.80增至0.863，随初始水头增加，长度比α逐渐增加，但增加幅度减小。图7表明，初始水头h由31 cm增至77 cm，右侧直径比β由0.869减至0.851，随初始水头增加，直径比β逐渐减小，但减小幅度减小，并渐趋稳定；将式(5)变形可得前后两级水力梯度之比ik+1/ik=1/(nβ4)，随径向距离增加，水力梯度减小，即ik+1/ik=1/(nβ4)<1，代入n=2计算得到直径比β>0.84，由此推断直径比β的渐趋稳定值为0.84。图8表明，初始水头h由31 cm增至77 cm，右侧的初级母管长度l0由4.671减至3.229，随初始水头增加，初级母管的长度减小；初始水头h越高，长度比α越大，由式(9)可知，距导流孔直线距离相等时长度比α越大，初级母管长度l0越小，所以初始水头h越高，初级母管长度l0越小。

图5 导流孔周水平向孔隙水压力分形拟合

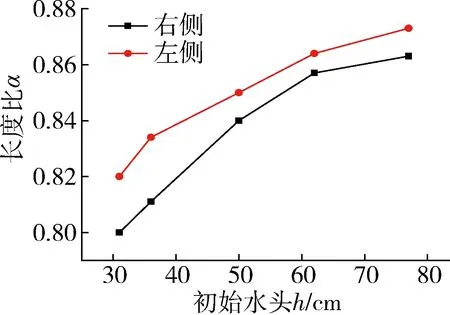
图6 初始水头h与长度比α关系

图8 初始水头h与初级母管长l0关系

4 结 论

1)假设水沿水平方向流入导流孔的通道为普遍存在的2分叉分形树状网络结构，基于Hagen-Poiseuille方程，提出导流孔周水平方向孔隙水压力计算公式，室内模型试验表明该计算公式有效可行。

2)在导流孔两侧形成大致呈对称状的降落漏斗，离导流孔越近孔隙水压力值下降越快，且很快接近导流孔，底面曲率很小，水面线较为平缓。

3)随初始水头增加，描述树状分叉网络的各级圆管长度比α逐渐增加，且增加幅度越来越小；但是各级圆管的直径比β和初级母管长度l0逐渐减小，并渐趋稳定，各级圆管的直径比β的稳定值为0.84。

[1] 邹国良.离子型稀土矿不同采选工艺比较：基于成本的视角[J].有色金属科学与工程，2012，3(4)：53-56.

[2] 黄小卫，张永奇，李红卫.我国稀土资源的开发利用现状与发展趋势[J].中国科学基金，2011(3)：134-137.

[3] 袁长林.中国南岭淋积型稀土溶浸采矿正压系统的地质分类与开采技术[J].稀土，2010，31(2)：75-79.

[4] 赵中波.离子型稀土矿原地浸析采矿及其推广应用中值得重视的问题[J].南方冶金学院学报，2000，21(3)：179-183.

[5] SELLEY R C.Elements of petroleum geology[M].2nd ed.San Diego：Academic Press，1998.

[6] 李瑞川，陈君若，刘显茜，等.分形多孔介质渗流特性的研究[J].陕西科技大学学报，2011，29(6)：47-50.

[7] 王世芳，吴涛，邓永菊.随机分布树状分叉网络渗流特性的分形研究[J].华中师范大学学报：自然科学版，2012，46(4)：406-409.

[8] Mandelbrot B B.The Fractal Geometry of Nature[M].New York：Freeman，1982.

[9] 徐鹏，郁伯铭，邱淑霞.裂缝型多孔介质的平面径向渗流特性研究[J].华中科技大学学报：自然科学版，2012，40(1)：100-103.

[10] Yu B M.Analysis of flow in fractal porous media[J].Applied Mechanics Reviews，2008，61(5).

[11] 邱淑霞，徐鹏，郁伯铭.各向异性多孔介质中径向渗流的分形分析[C].第十一届全国渗流力学学术大会，2011：472-477.

[12] Yu B M,CHENG P.A.fractal permeability model for bi-dispersed porous media[J].International Journal of Heat and Mass Transfer，2002，45(14)：2983-2993.

[13] 王洪丁，王观石，胡世丽，等.离子型稀土矿体孔径分布及其渗透性变化[J].科学技术与工程，2016，16(25)：51-56.

[14] 张克松，刘松玉.土力学[M].第三版.北京：中国建筑工业出版社，2010：34-35.

[15] 薛禹群.地下水动力学[M].北京：中国水利水电出版社，2009：64-65.

[16] 詹红兵，万军伟.水资源和环境工程中水平井研究简介[J].地球科学，2003，28(5)：511-516.

Distributionlawofhorizontalporewaterpressurearounddiversionconduit

HU Shili1，WANG Min1，WANG Guanshi1，2，HONG Bengen3，LUO Sihai1

(1.School of Architectural and Surveying & Mapping Engineering，Jiangxi University of Science and Technology，Ganzhou341000，China；2.Cold and Arid Regions Environmental and Engineering Research Institute，Chinese Academy of Sciences，Lanzhou730000，China；3.School of Resources and Environmental Engineering，Jiangxi University of Science and Technology，Ganzhou341000，China)

It is of great significance for calculating the recovery rate of the rare earth resources in-situ leaching to master the distribution law of pore water pressure around the diversion conduit.Assuming that the channel of water flowing into the diversion conduit horizontally is the ubiquitous2-branched fractal tree-like network structure，based on Hagen-Poiseuille equation，the horizontal pore water pressure distribution expression of the diversion conduit was put forward.The indoor model test results showed that they were effective to describe the seepage channel of the water flowing into the diversion conduit by using the2-branched fractal tree-like network structure；with increasing of the initial water head，the length ratio of the pipe at each level of the tree-like branched network gradually increased and the increasing range was smaller and smaller，but the diameter ratio and the length of the primary pipe gradually decreased，then became stable，diameter ratio of the pipe at all levels was stable at0.84.

diversion conduit；distribution law of pore water pressure；fractal tree-like network；in-situ leaching

2017-01-10责任编辑：赵奎涛

国家自然科学基金项目资助(编号：41602311；5166015；51674125)；江西省教育厅科技项目资助(编号：GJJ150658)；江西省教育厅科技落地计划项目资助(编号：KJLD14042)

胡世丽(1976-)，女，博士，副教授，主要从事土力学和渗流力学方面的研究，E-mail：hslqhd@163.com。

TU45

：A

：1004-4051(2017)09-0148-05