基于两点磁梯度张量的磁偶极子在线定位方法
2017-09-18刘继昊李夕海曾小牛刘代志
刘继昊,李夕海,曾小牛,刘代志
(火箭军工程大学,陕西 西安 710025)
基于两点磁梯度张量的磁偶极子在线定位方法
刘继昊,李夕海,曾小牛,刘代志
(火箭军工程大学,陕西西安710025)
针对Nara方法中目标磁感应强度难以准确测量的问题,提出了基于两点磁梯度张量的磁偶极子在线定位方法。该方法利用任意两点的磁梯度张量差分量与目标磁感应强度差分量定位磁偶极子。仿真实验结果表明,该方法定位成功率不受背景磁场的影响;相同条件下,该方法的定位成功率为44.69%,而以往改进方法最高定位成功率为37.65%。
磁梯度张量;磁偶极子;定位
0 引言
磁梯度张量较传统的磁探测量具有更为丰富的信息,更加有利于对磁性目标的定位和跟踪,为磁性目标探测提供了有效手段,相关理论也已成为磁探测领域的研究热点[1-3]。在磁性目标探测领域中,磁偶极子是一种重要的磁源等效模型[4]。基于磁偶极子等效模型和磁梯度张量的磁性目标在线定位方法应用广泛。
Nara等人[5]以定位射频识别标签为应用背景,提出了一种直接通过单点目标磁梯度张量和目标磁感应强度定位磁偶极子的方法。然而,实际应用中,存在着不能忽略的背景磁场,导致目标磁感应强度无法准确测量,从而导致Nara方法定位结果误差很大。针对该问题,李光等[6]将Nara方法中的磁梯度张量替换为磁感应强度二阶差分量,目标磁感应强度替换为磁感应强度一阶差分量,提出了不受背景磁场影响的新方法;于振涛等[7]则通过对Nara方法中的定位方程进行偏微分推导,提出了基于磁梯度张量垂向差分的目标定位改进算法;尹刚等[8]基于Nara方法,利用磁感应强度二阶差分量,结合磁梯度张量矩阵特征向量与目标参数的正交性,提出了一种新的定位方法。但是,根据仿真实验的结果,以上三种改进方法的定位误差虽然小于Nara方法,但仍然较大[9]。因此,本文针对上述问题,提出了基于两点磁梯度张量的磁偶极子在线定位方法。
1 Nara方法原理及其十字形张量测量系统
设M为磁偶极子的磁矩,r为张量测量点与磁偶极子的相对位置矢量,n为r的方向向量,r为r的模,μo为空气中的磁导率。如果不考虑背景磁场的存在,张量测量点处的磁感应强度B为:
(1)
与磁偶极子相对位置矢量为r+ndr的点处的磁感应强度B′为:
(2)
r+ndr处到r处的磁感应强度变化量为:
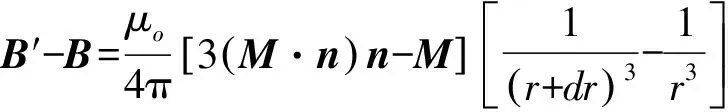
(3)
变化量又可以表示为:
(4)
联立式(3)式(4),可得:
r=-3G-1B
(5)
通过张量测量系统测得张量G后,再测定目标磁异常场的B,即可完成定位。
测量G所采用的十字形张量测量系统[5]如图1所示。
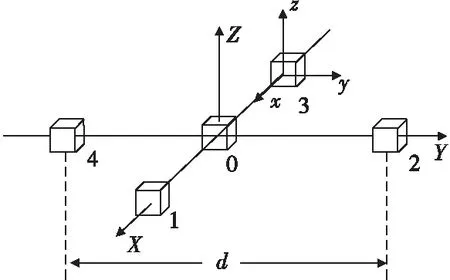
图1 十字形张量测量系统示意图Fig.1 Sketch map of cruciform tensor measurement array
测量系统共采用5个三轴矢量磁力计,其中1,3号磁力计的距离和2,4号磁力计的距离均为d(即为基线长度);0号磁力计位于十字中心,用于测量探测点的磁感应强度B;1,2,3,4号磁力计的测量结果B1,B2,B3,B4用于计算磁梯度张量。所有磁力计坐标系与测量系统坐标系对准,根据磁梯度张量的定义与性质,在此种测量方式下:
(6)
2 基于两点磁梯度张量的磁偶极子在线定位方法
2.1 方法原理
设测量张量的两个点A、B对应的位置矢量分别为rA,rA+Δr,目标所等效的磁偶极子的磁场用Bt表示,则根据式(5)有:
GArA=-3BtA
(7)
(8)
由式(8)减去式(7)得:
(9)
解得:
(10)
实际应用场景中,背景磁场多是地磁场,在测量系统所处的范围内可以认为地磁场是匀强磁场,用Be表示,三轴磁力计所测得的磁感应强度用B表示,在不考虑其他磁场干扰的情况下,在同一个坐标系下显然有:
BA=Be+BtA
(11)
BB=Be+BtB
(12)
由式(12)减去式(11)得:
BtB-BtA=BB-BA
(13)
代入式(10)可得:
(14)
式中,BA,BB,GA,GB可以通过测量得到,Δr由两点张量测量系统的设计决定,为已知量。
2.2 两点张量测量系统
根据2.1节所提方法的原理,本文设计了新型张量测量系统如图2所示。
图2中阵列共有8个坐标轴严格对准的三轴磁力计组成,其中1,2,3,4号磁力计组成边长为d的正方形张量阵列测量GA,计算公式为:
(15)


图2 两点张量测量系统示意图Fig.2 Sketch map of two-point tensor measurement system
2.3 方法步骤
结合方法原理以及所设计的张量测量系统,方法实现步骤如下:
1)读取磁力计1到磁力计8的磁感应强度测量结果Bi,(i=1,2,3,4,5,6,7,8);
2)计算得到GA,GB;
3)解算位置向量
(16)
3 仿真实验

定义定位误差e的计算公式为:
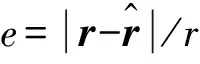
(17)

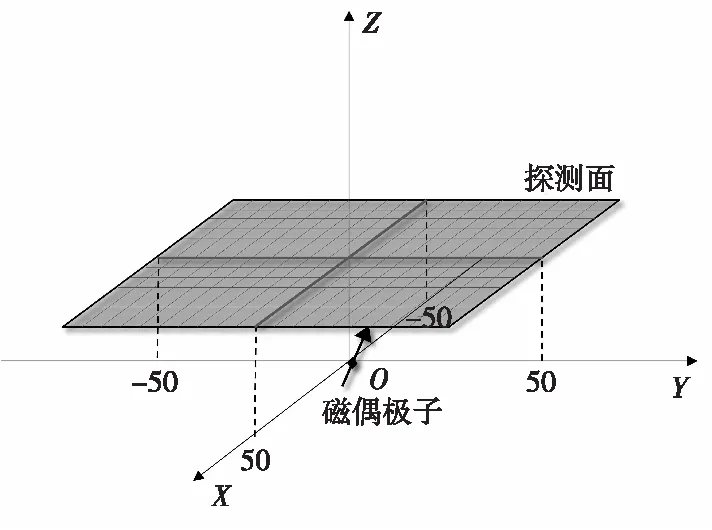
图3 算法仿真方法示意图Fig.3 Sketch map of simulation experiment
考虑到实际应用,定位误差大于10%时,即认为定位失败,在定位误差分布图中用白色网格表示定位失败的探测点,同时,定义定位成功的探测点占所有探测点的比例为定位成功率,用以衡量算法的性能。
3.1 仿真条件与结果分析
1)为了观察方法本身的误差,所有张量测量系统的基线长度d都取为1 m,在不考虑背景磁场和测量误差的条件下,对Nara方法和本文提出的方法进行仿真实验。
两种方法定位误差空间分布如图4(a)、图4(b)所示,由仿真结果可知,即使不存在背景磁场,方法本身仍存在误差。根据统计,Nara方法的定位成功率为99.50%,本文方法的定位成功率为98.62%。
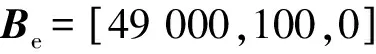

图4 无背景磁场情况下定位结果对比Fig.4 Results without background magnetic field

图5 有背景磁场情况下定位结果对比Fig.5 Results with background magnetic field
可以看到,由于背景磁场的存在,原Nara方法定位成功率降为0。本文方法成功定位区域覆盖半径最大。根据统计,各方法的定位成功率如表1所示,可知,本文所提方法定位成功率高于以往的改进方法。

表1 各方法定位成功率对比
统计每种方法完成一次定位的平均耗时作为衡量方法效率的指标,结果如表2所示。其中,李光改进方法和尹刚改进方法耗时最少,本文方法和于振涛改进方法耗时较多,但仍能满足在线实时定位的要求。笔者分析,本文方法和于振涛改进方法耗时较多的原因是二者都需要计算两个点的磁梯度张量。
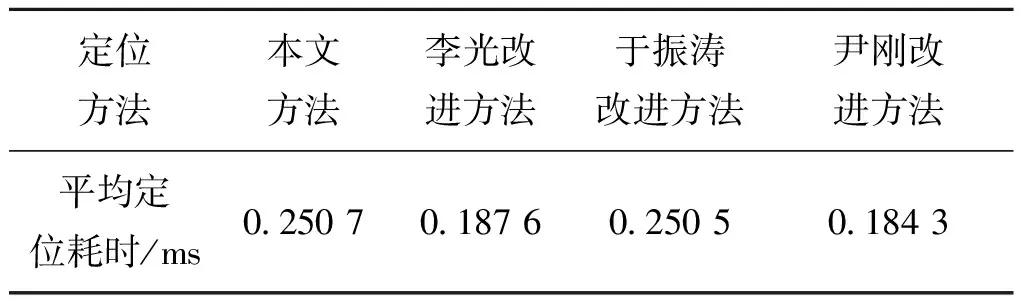
表2 不同方法的定位平均耗时比较
3)实际应用过程中,存在张量测量阵列基线长度d的选取的问题。保持仿真实验步骤2)中的其他条件不变,张量测量系统的基线长度依次取d=(0.1,1,2,3,4,5,6,7,8,9)m。对本文所提方法、李光改进方法、于振涛改进方法和尹刚改进方法进行仿真实验。
通过实验,得到每种方法的定位成功率随基线长度d的变化曲线如图6。

图6 四种方法定位成功率随基线长度的变化曲线Fig.6 Success rate-d curves of different methods
观察四条曲线的变化趋势,可知:定位成功率都随着基线长度d的增加而先增加后减小,本文方法在d=3 m时定位成功率最高(达83.95%),李光改进方法在d=5 m时最高(48.98%),于振涛改进方法在d=4 m时最高(70.25%),尹刚定位方法在d=7 m时最高(70.27%),所以本文方法的最高定位成功率在四种方法中最高;在d≤6 m时,本文方法的定位成功率一直高于其他三种改进方法;
观察发现,定位失败区域随着噪声均值的增加同时发生两种变化:一种是呈环形向内扩张;一种是从成功定位区域的“裂缝”处不断扩张。前者产生的原因是,磁感应强度随距离很快衰减,而噪声均值不变,造成信噪比随距离快速减小,以至于定位失败;后者的原因则与方法本身的特性有关,下文中做详细阐述。
3.2 误差原因分析与应对思路
本文方法在不存在干扰的条件下定位成功率只有98.62%,而该方法的理论推导中并未涉及到近似,定位成功率应为100%。笔者推测产生此种现象的原因是仿真过程中计算机的硬件限制产生的误差(如字长产生的截断误差等)在方法中方程组不适定时被放大。对方法原理进行进一步分析可知,本文方法中式(14),等价于解算线性方程组
(18)

在仿真过程中,计算BA,BB以及计算GA,GB时所用的磁感应强度都是利用磁偶极子的磁场模型通过计算机模拟得到的,由于计算机计算精度的限制,不可避免的会产生截断误差,对方程右侧的观测量造成扰动。截断误差造成的扰动虽然极其微小,但在接近奇异的系数矩阵作用下,依然会对定位结果产生恶劣影响。

对于Nara方法仿真误差的产生原因,采用相同的分析思路,对比图4(a)与图4(c)可以得到同样的结论。

所以,如何在式(18)不适定时,尽量减小定位结果解算的误差是未来研究的一个方向。
4 结论
本文提出了基于两点磁梯度张量磁偶极子在线定位方法。该方法利用任意两点的磁梯度张量差分量与目标磁感应强度差分量定位磁偶极子。仿真实验结果表明,该方法定位成功率不受背景磁场的影响;相同条件下,该方法的定位成功率为44.69%,而其他基于Nara方法的改进方法定位成功率最高为37.65%。方法解算过程中出现的不适定问题有待进一步解决。
[1]于振涛,吕俊伟,毕波,等. 四面体磁梯度张量系统的载体磁干扰补偿方法[J]. 物理学报, 2014, 63(11): 139-144.
[2]张光,张英堂,尹刚,等. 基于线性误差模型的磁张量系统校正[J]. 吉林大学学报(工学版), 2015, 45(3): 1012-1016.
[3]张光,张英堂,尹刚,等. 一种张量探测系统载体的磁张量补偿方法[J]. 地球物理学报, 2016, 59(1): 311-317.
[4]张朝阳,肖昌汉,高俊吉,等. 磁性物体磁偶极子模型适用性的试验研究[J]. 应用基础与工程科学学报,2010,05:862-868.
[5]Nara T, Suzuki S, Ando S. A closed-form formula for magnetic dipole localization by measurement of its magnetic field and spatial gradients[J]. Magnetics, IEEE Transactions on, 2006, 42(10): 3291-3293.
[6]李光,随阳轶,刘丽敏,等. 基于差分的磁偶极子单点张量定位方法[J]. 探测与控制学报, 2012, 34(5): 50-54.
[7]于振涛,吕俊伟,樊利恒,等. 基于磁梯度张量的目标定位改进方法[J]. 系统工程与电子技术, 2014, 36(7): 1250-1254.
[8]Yin A G, Zhang Y, Fan H, et al. Magnetic dipole localization based on magnetic gradient tensor data at a single point[J]. Journal of Applied Remote Sensing, 2014, 8(1):5230-5237.
[9]刘继昊,李夕海,于帆. 基于磁梯度张量的磁异常在线定位方法分析与评估[C]// 国家安全地球物理丛书(十二).西安:西安地图出版社,2016:19-30.
AnOnlineMagneticDipoleLocationMethodBasedonMagneticGradientTensorofTwoPoints
LIU Jihao, LI Xihai, ZENG Xiaoniu, LIU Daizhi
(Rocket Force University of Engineering, Xi’an 710025, China)
Nara’s method is affected greatly by the background magnetic field as the magnetic induction of the target is requisite. To solve this problem, a novel online location method which used the magnetic gradient tensor and the magnetic induction of two points to locate the magnetic dipole was proposed in this paper. The result of simulation experiments indicated that the location precision of the proposed method was free from the affection of the uniform background magnetic field and the localization success rate of the promoted method was 44.69%, while the others improved Nara methods was smaller than 37.65%.
magnetic gradient tensor, magnetic dipole, location
2017-02-21
:刘继昊(1993—),男,河南新乡人,硕士研究生,研究方向:磁性目标探测。E-mail:liujihao1993@163.com。
P318.4
:A
:1008-1194(2017)04-0108-05
