样本列信息与自适应邻域图的局部保持投影*

王海燕，林克正，马 龙，李 骜

哈尔滨理工大学 计算机科学与技术学院，哈尔滨 150080

样本列信息与自适应邻域图的局部保持投影*

王海燕，林克正+，马 龙，李 骜

哈尔滨理工大学 计算机科学与技术学院，哈尔滨 150080

k近邻；局部保持投影；自适应邻域；样本列；结构特征

1 引言

近年来，基于子空间分析的人脸特征提取方法成为人脸识别领域的研究热点[1]。基于子空间的人脸特征提取方法，将人脸看作一个处于高维空间中的整体[2]，选择线性或者非线性映射，将样本数据从高维空间映射到一个低维空间内，同时保持数据在原有高维空间中的内在本质结构特征[3]。经过多年研究，人们已提出了一些线性的人脸特征提取算法，如主分量分析[4]（principal component analysis，PCA）、线性鉴别分析[5]（linear discriminant analysis，LDA）等。很多研究者发现人脸图像空间的高维样本数据极可能分布于一个非线性流形空间上[6-8]，因此非线性的基于子空间分析的流形学习方法应运而生。例如，等距映射算法[8]（isometric mapping，ISOMAP）和局部线性嵌入算法[9]（locally linear embedding，LLE）在Science杂志的发表，以及随后被提出的拉普拉斯特征映射[10]（Laplacian eigenmap，LE），均促进了流形学习方法的研究。但是上述这些算法对新定义的样本数据的泛化能力不强。据此，He等人提出了局部保留投影[11]（locality preserving projection，LPP）。

LPP算法继承了拉普拉斯算法[10]的思想，即在降维过程中需要通过构造邻接图来保持原高维空间中样本数据之间的结构特征。然而，LPP是一种无监督的降维方法，没有利用样本的类别信息，对有监督的学习问题的识别效果不是太好。因此，有研究者提出了有监督的LPP算法——鉴别局部保持投影（discriminant locality preserving projection，DLPP）[12]。然而这些LPP算法及其变体在构建邻接图时采用的是一种全局性的k近邻构图方法，即假设每个样本的近邻个数是一样的，这样很容易造成投影空间中样本的局部结构失真，同时参数k的选择也十分困难。针对这个问题，有人提出了一种局部保持鉴别投影方法[13]，解决了全局参数k的选择问题，样本的局部结构也得到了保持。然而在构建邻接图时，采用的是将二维结构的图片样本转化成了一维向量形式，样本的内部结构信息利用得不够，而这些二维结构信息很有可能帮助构建更合理的邻接图，从而提高识别率。因此，本文提出一种全新的自适应确定邻域的构图方法——基于样本的列信息的自适应邻域构图方法（adaptive neighbor and corresponding columns on graph，ANCCG）。在该方法中，将一个图像样本分成若干个列样本，每个列样本的列近邻由该列样本与对应该位置的其他图像样本的列样本的相关关联度来确定。然后比较两个样本之间的所有列近邻对个数和总体样本平均近邻对个数，来决定两个样本最终的近邻关系，然后构造样本的近邻图。将该方法与LPP算法结合形成了ANCCG-LPP算法。为了提高ANCCG-LPP算法的识别率，通过加入样本类别信息提出了监督的ANCCG-LPP算法（supervised ANCCG-LPP，SANCCG-LPP）。整个构图过程是一个自适应确定邻域的过程，消除了参数k选择困难问题及选择不当所造成的样本空间的局部信息缺失或者过于零散问题。另外，由于充分利用了样本的二维结构列特征，这种方式更好地挖掘样本之间的近邻关系，增强了样本的局部流形结构的表征能力。

2 局部保持投影算法

LPP算法是一个非监督的基于邻接图的流形学习算法，它的宗旨是尽可能地保持投影到低维空间后的样本在原始高维空间的流形结构[14]。因此，LPP算法就是要寻找一组最佳投影矢量集，以使投影后样本能最大程度地保持原高维空间中顶点间的相似性，以使样本的局部离散度最小[15]。

设高维空间中含有N个样本的数据集合为X={x1,x2…,xN}，LPP的目标是找到一个低维表示Y=ATX。令{V,E,W}表示一个对应样本集的邻接图，V是一个样本点集合；E表示图中两个点之间的边；W表示带权邻接矩阵，反映了样本点集合中样本之间的关系。

2.1 LPP构图方式

2.1.1 k近邻法构造邻接矩阵E

k近邻法：采用欧式距离来衡量样本空间中数据点的远近关系，找出k个距离样本xi最近的点组成样本xi的近邻集合，集合中所包含的样本点都是样本xi的k近邻；如果节点xj是xi的k近邻或者xi是xj的k近邻，则在节点xi与xj之间用一条边相连；最后在构造邻接矩阵时，有边相连的标记为1，没有边相连的标记为0。

2.1.2 构造权值矩阵

在确定好样本的邻接矩阵之后，仅仅是基本确定了样本点之间的邻接情况，还需通过在边上加权重来描述邻接图中两个样本点之间的边的重要性。因此为了进一步描述样本点之间的相似程度和彼此间的依赖程度，需要构造带权邻接矩阵。LPP算法的权值矩阵的构造方式如下。

热核法：如果 xi与xj相连接，则权值wij=exp(-||xi-xj||2/t),否则wij=0。其中，t是核参数；||xi-xj||表示xi与xj间的欧氏距离；W∈RN×N是一个对称半正定矩阵。

2.2 LPP算法目标函数

为了保持原始高维空间中样本之间的相似性和局部邻域结构，需要使样本的局部离散度最小为目标。因此LPP的目标函数如式（1）所示：

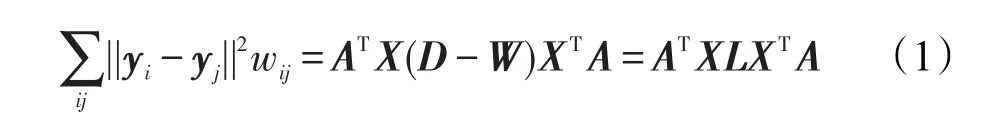
其中,W=(wij)是采用热核法构造的权值邻接矩阵；D是对角矩阵，为拉普拉斯矩阵且L=D-W。

为了求得最优投影矢量集，将ATXDXTA=I作为限制条件加入到LPP的目标函数中去。这里，I是单位矩阵。因此，最优投影矢量集可通过下式求得：

投影矩阵A∗可通过式（3）的前d个最小的特征值集合 λ=[λ1,λ2,…,λd]对应的特征向量得到。

假定求解出来的特征向量为 [α1,α2,…,αd]，则经过LPP算法，高维空间样本的低维表示为Y=ATX。

3 ANCCG-LPP算法

3.1 样本列信息的自适应构图方式

假设含有N个训练样本的图片集合为I={I1,I2…,IN}，对于一个图像样本Ii（尺寸为 p×q，这里 p表示样本图片的高度，q表示样本图片的宽度）。图片集合I的向量形式的集合可表示为X={x1,x2…,xN},xi∈RD。首先，对于一个图像样本Ii，将其分成l个列(l=1,2,…,q)，令表示样本Ii的第l列，表示对应样本Ii的第l列的向量形式。对于所有其他样本图片矩阵的第l列，通过一种自适应的方式来确定样本的每个列样本的列近邻和邻域，最终确定样本近邻。分以下几个步骤来确定样本xi的邻域。

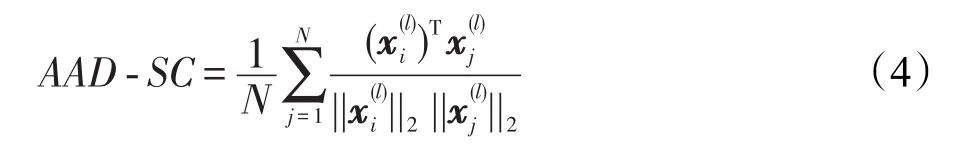
定义1样本列的平均相关度可通过式（4）计算。上式的意义在于：计算样本图片Ii对应第l位置的列样本与其他样本中对应l列的列样本的平均关联度，描述的是两个样本之间对应列样本之间的相似性。

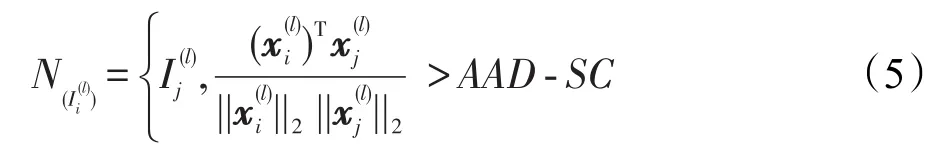
步骤3确定样本之间的列近邻对的个数。

Nij表示两个样本之间列近邻对的个数，即样本Ii和Ij之间有多少对列向量成为列近邻，初始的时候Nij=0。Nij代表了样本之间的相似度。样本之间列近邻的确定可通过下面的式子来计算：

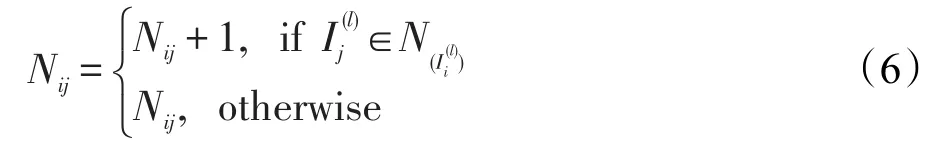
步骤4构造邻接矩阵和权值矩阵。

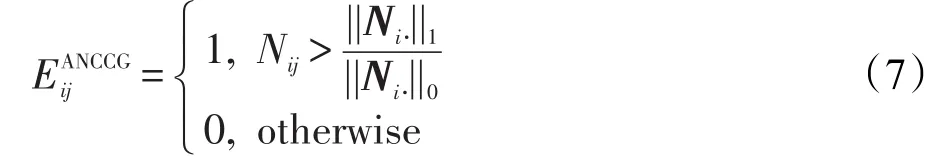
其中，Ni·=[Nij](j≠i,j=1,2,…,p)，它反映了样本 Ii对于其他所有样本的相似度。||Ni·||0表示向量Ni·中非零元素的个数，实际计算的是有多少个样本与样本xi之间的列近邻个数不为0，它是向量Ni·的L0范数。||Ni·||1表示向量Ni·中所有非零元素绝对值的累加和，实际是对所有样本与xi样本之间的列近邻对个数进行求和，它是向量Ni·的L1范数。因此，上式可解释为：Ii对于所有其他样本的平均相似度为，如果Ii和Ij之间的样本相似度大于这个值，那么让Ij成为Ii的一个近邻，即。

样本的带权邻接矩阵，通过以下公式来计算：

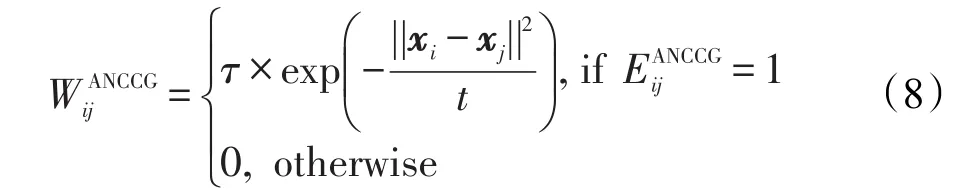
上述这种基于样本列信息的自适应邻域构图方法的优点在于：（1）首先对样本图片进行列划分，利用划分后的列图片信息进行自适应列邻域的寻找，这样确定的样本相似度，充分利用了原始样本的二维结构信息。（2）整个过程不需要参数的设置，避免了传统k近邻方法的参数k的选择所带来的嵌入空间分散琐碎和局部空间问题。（3）权值矩阵的构造通过加入一个反映两个样本相似度比重的参数，来衡量两个边之间的重要程度，更有助于真实地反映样本之间的近邻关系。（4）本文的邻接矩阵和权值矩阵的非对称性的特点，更好地描述了样本之间的真实邻域关系和样本的流形结构。

3.2 目标函数及最优投影矢量

令 A表示投影矩阵，xi的投影为yi，即yi=ATxi，则在嵌入空间中，希望样本能保持局部结构不变性，即新投影后的样本保持其在原始高维空间的邻域结构关系，也即使样本在变换后的低维空间中的局部离散度最小。因此目标函数可表述为：

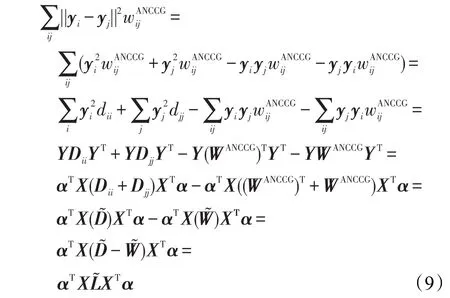
其中，矩阵D=[dii](i=1,2,…,N)是一个对角矩阵，dii=，并 且是对称矩阵，是对角矩阵，͂中的每个行元素是中的对应每一行的所有列元素的累加和，满足拉普拉斯矩阵的条件。因此，是拉普拉斯矩阵，加入约束条件，因此，本文算法的目标函数为：

投影矩阵A∗可通过求解式（11）的前m个最小的特征值λ对应的特征向量得到。

由于在实际实验中，人脸样本的数量N往往是有限的，远远小于样本数据的维数n，因此经常面临着小样本问题。这种情况下，为奇异矩阵，这就为投影矢量的求解带来困难，因此在进行本文算法之前，先将高维空间的样本数据通过主成分分析法进行降维，之后采用本文所提出的ANCCG-LPP算法进行特征提取工作。

3.3 监督的ANCCG-LPP

ANCCG-LPP算法在构造图的过程中，一直考虑如何利用好样本的结构信息来更好地揭示样本之间的近邻关系。为了提高本文算法的识别性能，通过加入样本的类别信息，去除不相关样本的干扰。因此，由3.2节ANCCG-LPP的构图方法结合样本的类别信息，提出了监督的ANCCG-LPP（SANCCG-LPP）。SANCCG-LPP算法的目标函数的形式与ANCCGLPP的相同，投影向量的求解过程也基本相同。在计算边权的时候考虑了类别信息，式（12）展示了SANCCG-LPP算法的边权重矩阵的定义方式：

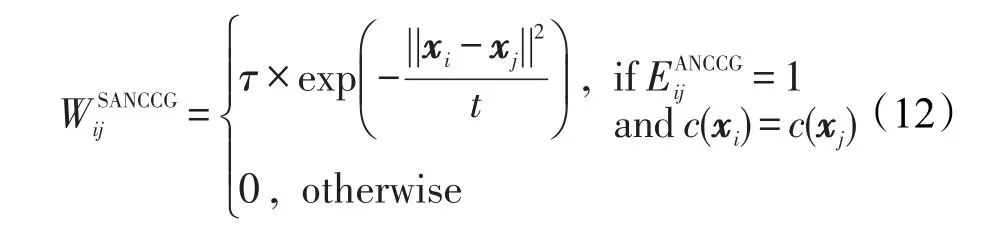
式中，c(xi)和c(xj)分别表示xi和xj所属的类标签。在实际计算过程中，将式（9）中的边权重矩阵公式用式（12）替换，即可得到SANCCG-LPP算法的目标函数公式，通过加入相应的约束条件求出对应的特征向量。

3.4 本文算法步骤

根据前面的推导和分析，以ANCCG-LPP算法为例，具体阐述该算法的具体操作步骤。

步骤1对原始高维空间中的样本进行PCA降维至k维空间。利用公式计算样本的总体散布矩阵，采用奇异值分解的思想，间接求出总体散布矩阵对应的前k个非零的最大特征值对应的特征向量，作为最优投影矢量集，即APCA=[η1,η2,…,ηk]，最终得到原始样本经 PCA 降维至低维空间的表示为

步骤2构造邻接图ANCCG。对图片进行分块，分成l列，对每个图片列样本利用式（4）、（5）得出样本对应的列近邻点集；根据式（6）确定任意两个样本xi和xj之间列近邻对个数；根据式（7）计算邻接矩阵，确定样本的近邻关系；利用式（8）计算样本的带权邻接矩阵WANCCG，同时计算带权邻接矩阵的转置(WANCCG)T。

步骤4通过目标函数求最优投影矩阵。计算式（11）的前d个最小特征值对应的特征向量[α1,α2,…,αd]，得最优投影矩阵为 AANCCG=[α1,α2,…,αd]。

步骤6对测试样本采用步骤1～步骤4，得到对应测试样本的最优投影，采用最近邻分类器进行分类。

步骤7对于监督的算法SANCCG-LPP，最优投影的计算和求解过程与上述步骤一样，只需将公式中有的地方换成即可。

4 实验结果与分析

为了验证ANCCG-LPP和SANCCG-LPP算法的有效性，将本文算法和其他所有算法都统一在ORL人脸库和Extended Yale B人脸库上进行实验，实验中将Matlab R2014作为测试平台，所有算法的分类器都采用最近邻分类器，采用的核参数范围为{105,106,107}，结果取最佳识别率。

ORL人脸库，由10个人的400幅图像组成，分别在不同的面部表情、姿态和细节有轻微变化的情况下拍摄，其中有些图像是在不同的时期拍摄的。在实验时为计算方便，统一将图片进行裁切处理，只保留脸部区域。本文将每幅图像的大小调整为32×32像素。

Extended Yale B人脸库，由28个人的16 128幅图像组成，分别在不同姿态和不同光照条件下拍摄。本实验中统一对图片进行裁切，只保留脸部区域，并将图片大小设置为32×32像素。

4.1 结构变化实验

为了与传统的k近邻构图方法形成对比，比较出本文算法在构造图的过程中样本空间结构关系变化。本实验从ORL人脸库选取10张照片，其中1、2、4、6、7是属于同一个人的照片，3和5是另外一个人的照片，其他照片是随机选取的他人照片，形成一个实验数据集。在这个数据集上分别采用传统k近邻构图方法和本文ANCCG的构图方法。按照本文构图方法得出的样本相似度矩阵(Nij)如图1。图2和图3分别展示了ANCCG构图方法和k近邻构图方法的邻接矩阵。

图1是在ORL人脸库的样本集上用本文方法计算出来的相似度矩阵。图中不带圆圈的数字表示的是两个样本之间的相似度情况。图中第2行第4列的值为17，表示的是用本文自适应列近邻法计算出来的列近邻数，即样本4中有17列成为了样本2的列近邻。图中第4行第2列的值为14，即样本2中有14列成为了样本4的列近邻。可见，本文方法的相似度矩阵是不对称的，这就更好地反映了样本之间的结构和关系。

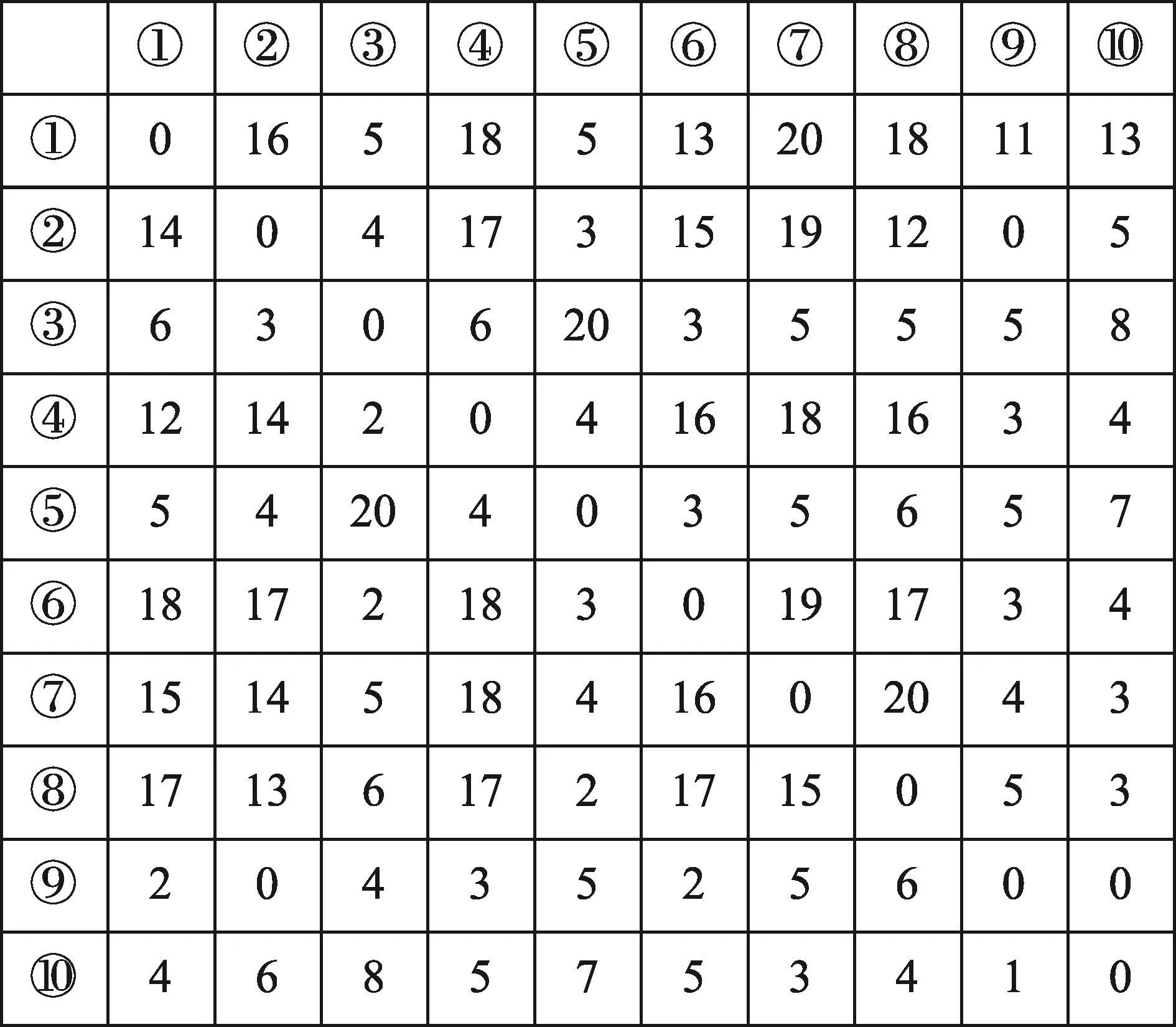
Fig.1 Similarity matrix ofANCCG method图1 ANCCG算法的相似度矩阵

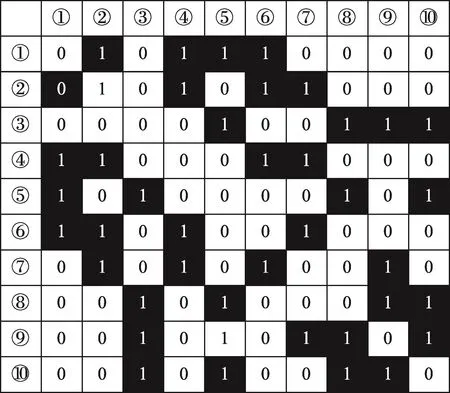
Fig.2 Adjacency matrix ofANCCG method图2 ANCCG算法的邻接矩阵

图2、图3是在实验数据集计算出来的ANCCG邻接图的邻接矩阵和k邻接图的邻接矩阵。黑色方块表示的是两个样本是邻接的。从图中可以看出，在ANCCG邻接图的邻接矩阵中，邻接的样本大致都属于同一个人，而在k邻接矩阵中，这种正确的样本邻接关系没有得到很好的体现。例如，在ANCCG邻接图的邻接矩阵中的第5行，只有样本3和5邻接，事实上样本3和5也是来自同一个人；k邻接图的邻接矩阵中的第5行，样本1、3、8、10都和样本5邻接，而事实上，只有样本3是和样本5来自同一人，样本1、8和10分别来自不同的人。同时传统的k近邻图的邻接矩阵是对称的，而ANCCG图构造出来的邻接图是不对称的，这更好地体现了真实样本空间的情况。

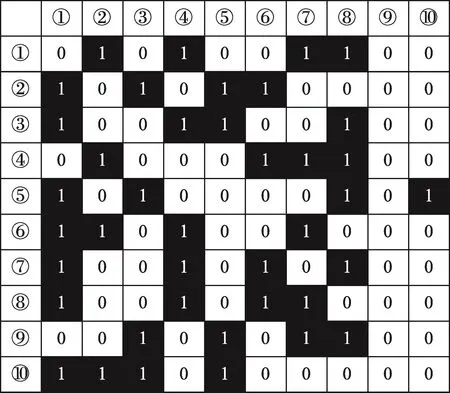
Fig.3 Adjacency matrix of k adjacency graph图3 k邻接图方法的邻接矩阵

4.2 识别率实验

为验证本文方法的识别率情况，各算法的识别率实验选择在ORL、Yale Extended B人脸库上进行，将算法 LPP[11]、LDP[12]、LPDP[13]与本文提出的 ANCCGLPP、SANCCG-LPP算法进行对比分析，其中在传统k近邻构图方法中，k近邻参数的选择范围是{1,2,…,10}。实验结果主要从两方面进行分析：（1）分析特征维数与识别率的关系；（2）分析样本数与识别率的关系。

4.2.1 特征维数与识别率的关系

ORL人脸库中，每人随机选择5张作为训练集，其他的作为测试集，即训练样本200张图片，测试样本200张图片。Yale Extended B人脸库中对于每一个志愿者分别随机选择50张图片作为训练样本，其他的作为测试样本。实验中参数k的取值范围(k=3,4,5)，每个实验重复20次，最后选取最佳识别率结果。图4、图5分别显示了样本在ORL、Yale Extended B人脸库上各算法特征维数与识别率的关系。

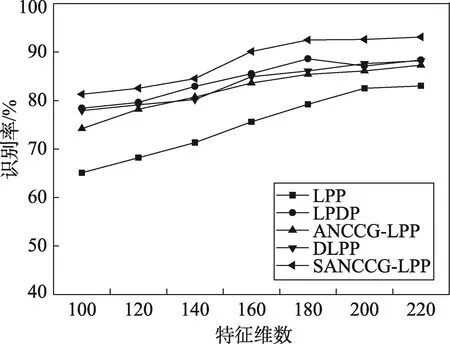
Fig.4 Recognition rate comparison on ORL face database图4 ORL人脸库的识别率对比

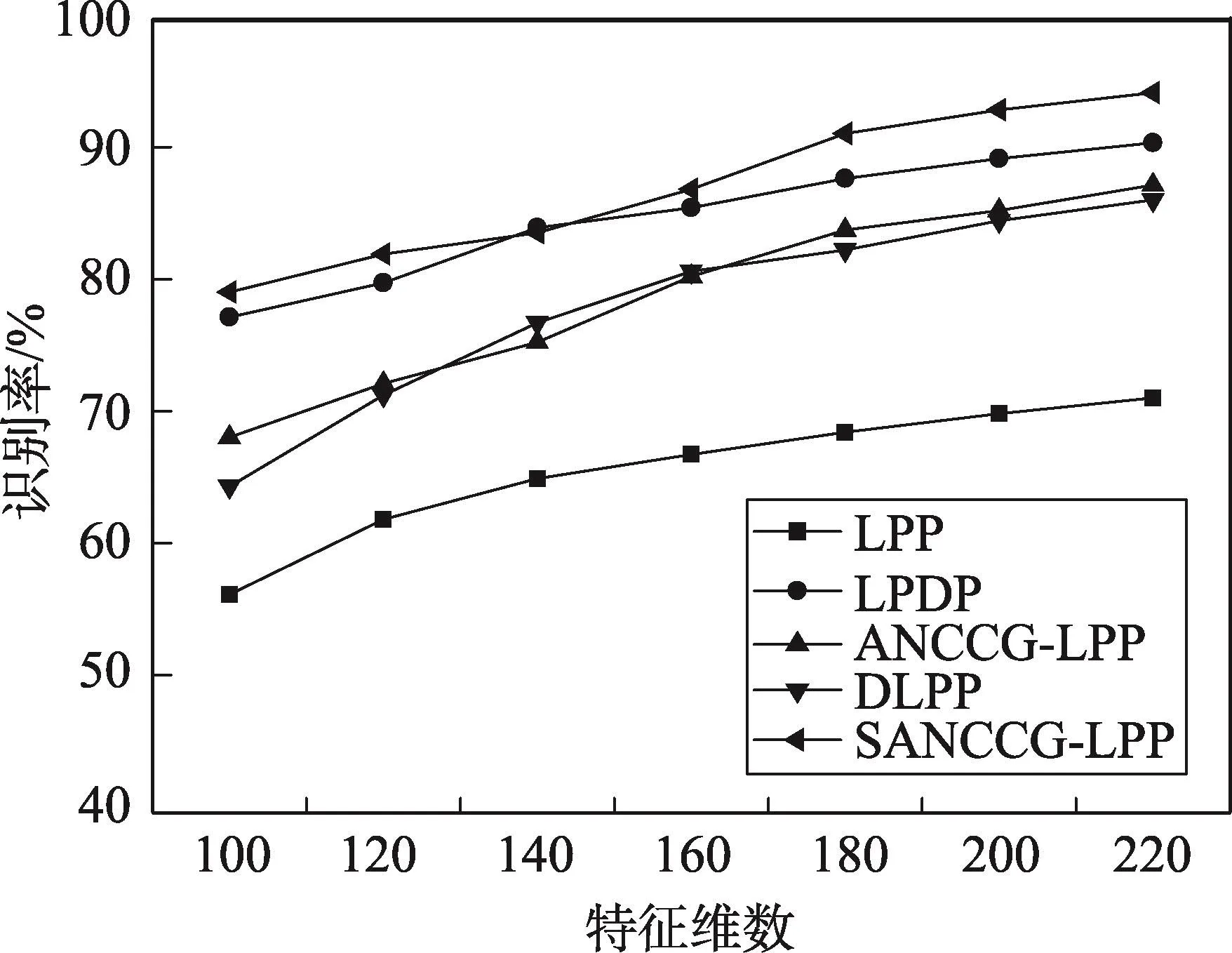
Fig.5 Recognition rate comparison on Yale Extended B face database图5 Yale Extended B人脸库的识别率对比

由图4、图5可知，在ORL人脸库和Yale Extended B人脸库中，随着特征维数的增加，本文ANCCG-LPP算法的识别率都比LPP算法的识别率有显著提升。然而由于ANCCG-LPP算法没有利用样本的类别信息，在ORL人脸库的实验结果显示，ANCCG-LPP算法的识别率要比利用样本类别信息的DLPP、LPDP算法略低。在Yale Extended B人脸库的实验结果显示，在特征维数大于160以后，ANCCG-LPP算法的识别率高于DLPP。这可能是因为随着特征维数的增加，样本内部结构信息的影响逐渐增加。相比于LPP算法的识别率，本文算法在Yale Extended B人脸库的识别率比在ORL人脸库上的识别率提高得较为明显，而由于Yale Extended B人脸库的光照、姿态条件更加复杂，可见本文算法在人脸图像光照、姿态、表情比较复杂的情况下的识别率比较理想。本文提出的SANCCG-LPP算法不仅充分利用了样本的二维结构的列样本特征，同时加入了样本的类别信息，因此它的识别率是最高的。

4.2.2 样本数与识别率的关系

在训练样本数与识别率关系的实验中，ORL人脸库上的实验选择了40个志愿者，每个人分别取2、3、4、5张图片作为训练样本集，其他的为测试样本集，即组成了4个训练样本集/测试样本集组合对80/320,120/280,160/240,200/200；Yale Extended B人脸库中，随机选择包含了不同姿态、光照和表情的16个志愿者的人脸图像，每个人分别随机选取20、30、40、50幅作为训练样本，对分别由320幅、480幅、640幅、900幅图像组成的训练样本集采用相同的测试集合，对应训练集中的每个志愿者选择50幅图片共800幅图像作为测试样本集。为了考查几种算法的识别率大小及其识别率波动范围情况，在两个人脸库中所选的训练样本/测试样本组都进行10次重复实验，最后结果取平均识别率。对应ORL人脸库和Yale Extended B人脸库中不同算法的识别率与训练样本数的关系情况如表1和表2所示。表1和表2中的训练样本数是选取一个志愿者的不同数量的图像作为训练样本。

由表1可知，不同的训练样本数情况下，各算法的识别率都是随着训练样本数的增加而提高的，LDP、LPDP、本文算法都较LPP的识别率有很大提高。随着训练样本数的增加，本文算法的识别率提高的幅度最大，样本数的增多，为本文算法在通过列信息特征确定样本间的相似程度的过程提供较大的参考价值，使得本文算法能充分发挥样本二维结构中列样本信息的优势。类别信息的加入，使得算法识别率进一步提升。同时各算法在进行重复实验时，识别率在一定范围内变化。

相比于ORL人脸库上的实验结果，由表2中各算法识别率后面的数字可知，在Yale Extended B人脸库中进行实验的所有算法的识别率的波动范围较大，这是因为Yale Extended B人脸库的人脸图像的表情、姿态、光照更为复杂，导致识别率上下波动更加明显。本文算法较其他算法的波动幅度小，说明算法更加稳定。表1和表2的结果都表明训练样本数量对识别率的重要影响。在ORL人脸库中的实验结果显示ANCCG-LPP算法的各个训练样本下的识别率都要略低于DLPP、LPDP这两种利用了样本鉴别信息的算法；而在Yale Extended B人脸库的结果则表明ANCCG-LPP算法的识别率要高于DLPP，但仍比LPDP低。这说明ANCCG构图方式能对复杂情况如姿态、表情、光照的人脸图像进行更有效的投射。ORL人脸库中的图像情况相对简单，类别信息发挥了重要的作用。

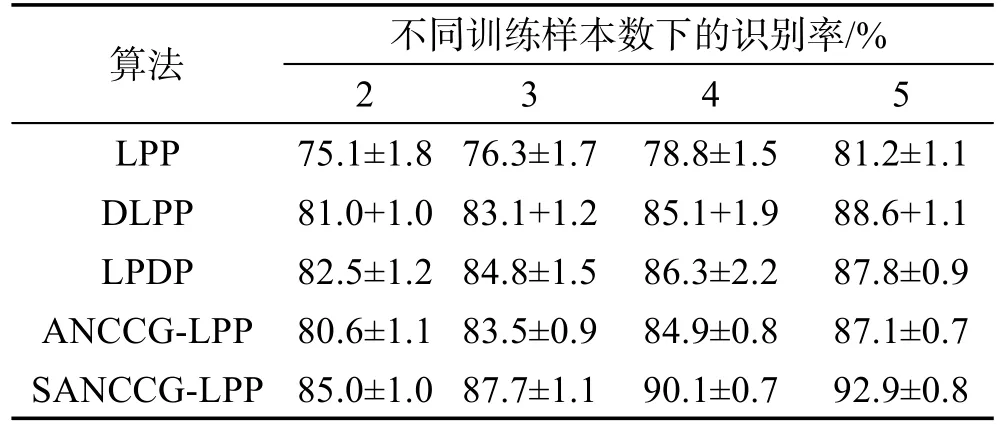
Table 1 Recognition rate comparison on ORL face database with different methods表1 在ORL人脸库中不同算法的识别率对比

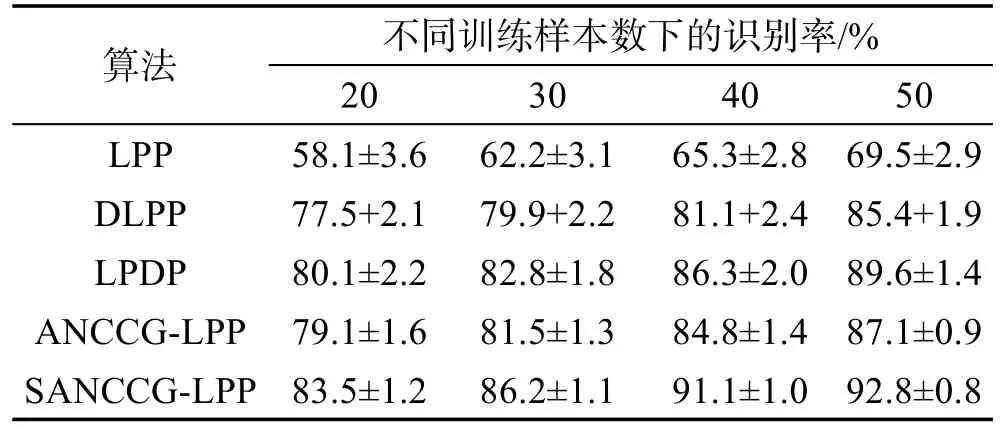
Table 2 Recognition rate comparison on Yale Extended B face database with different methods表2 在Yale Extended B人脸库中不同算法的识别率对比

5 结束语

本文充分考虑传统k近邻构图方法中全局k值的选择方式所带来的空间结构零散或者损失空间结构信息等问题，结合人脸图像样本的内部结构信息，提出了根据样本的内部结构信息来自适应确定邻域的方法。一方面充分利用了人脸图像的原始结构信息，更好地反映样本之间的近邻关系，构造一个样本局部流形结构更加紧凑的嵌入空间，为分类打下基础；另一方面，基于样本的二维结构信息来自适应地获取样本邻域的方法，解决了参数k的选择困难问题，提高了样本空间的信息表征能力，更好地描述了样本空间的数据分布。最后还加入了样本类别信息，进一步提高了算法的识别率。实验结果表明：在人脸图像情况复杂时，ANCCG-LPP算法能最大程度地发挥样本内部结构列信息的作用来自适应地构造样本局部流形空间结构。

[1]Gu Xiaohua,Gong Weiguo,Yang Liping.Supervised graghoptimized locality preserving projections[J].Optics and Precision Engineering,2011,19(3):672-680.

[2]Deng Sujuan,Zhou Xinyi,Tang Nianqing.Research and design of face recognition system combined with subspace projection and manifold learning[J].Journal of Chengdu Normal University,2015,31(3):109-112.

[3]Wang Yongmao,Li Geng.Local discriminant projection algorithm based on complete adaptive neighborhood graph embedding[J].Journal of Data Acquisition and Processing,2015,30(6):1271-1278.

[4]Turk M,Pentland A.Eigenfaces for recognition[J].Journal of Cognitive Neuroscience,1991,3(1):71-86.

[5]Belhumeur P N,Hespanha J P,Kriegman D J.Eigenfaces vs.Fisherfaces:recognition using class specific linear projection[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,1997,19(7):711-720.

[6]Cui Peng,Zhang Rubo.A semi-supervised coefficient selection method for face recognition[J].Journal of Harbin Engineering University,2012,33(7):855-861.

[7]Belkin M,Niyogi P.Laplacian eigenmaps for dimensionality reduction and data representation[J].Neural Computation,2003,15(6):1373-1396.

[8]Tenenbaum J B,de Silva V,Langford J C.A global geometric framework for nonlinear dimensionality reduction[J].Science,2000,290(5500):2319-2323.

[9]Roweis S T,Saul L K.Nonlinear dimensionality reduction by locally linear embedding[J].Science,2000,290(5500):2323-2326.

[10]Belkin M,Niyogi P.Laplacian eigenmaps and spectral techniques for embedding and clustering[J].Advances in Neural Information Processing Systems,2002,14(6):585-591.

[11]He Xiaofei,Yan Shuicheng,Hu Yuxiao,et al.Face recognition using Laplacian faces[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2005,27(3):328-340.

[12]Yu Weiwei,Teng Xiaolong,Liu Chongqing.Face recognition using discriminant locality preserving projections[J].Image and Vision Computing,2006,24(3):239-248.

[13]Zhao Zhenhua,Hao Xiaohong.Linear locality preserving and discriminating projection for face recognition[J].Journal of Electronics&Information Technology,2013,35(2):463-467.

[14]Li Bin.Research of feature extraction method based on GIST feature and manifold learning[D].Changchun:Jilin University,2015.

[15]Huang Pu,Tang Zhenmin.Parameter-free locality preserving projections and face recognition[J].Pattern Recognition and Artificial Intelligence,2013,26(9):865-871.

附中文参考文献：

[1]辜小花,龚卫国,杨利平.有监督图优化保局投影[J].光学精密工程,2011,19(3):672-680.

[2]邓素娟,周鑫燚,唐年庆.结合子空间投影和流形学习的人脸识别系统研发[J].成都师范学院学报,2015,31(3):109-112.

[3]王永茂,李赓.完备自适应近邻图嵌入的局部鉴别投影算法[J].数据采集与处理,2015,30(6):1271-1278.

[6]崔鹏,张汝波.半监督系数选择法的人脸识别[J].哈尔滨工程大学学报,2012,33(7):855-861.

[13]赵振华,郝晓弘.局部保持鉴别投影及其在人脸识别中的应用[J].电子与信息学报,2013,35(2):463-467.

[14]李斌.基于GIST特征和流形学习的特征抽取方法的研究[D].长春:吉林大学,2015.

[15]黄璞,唐振民.无参数局部保持投影及人脸识别[J].模式识别与人工智能,2013,26(9):865-871.

WANG Haiyan was born in 1988.She is an M.S.candidate at Harbin University of Science and technology.Her research interests include image processing and pattern recognition,etc.

王海燕（1988—），女，黑龙江齐齐哈尔人，哈尔滨理工大学硕士研究生，主要研究领域为图像处理，模式识别等。

林克正（1962—)，男，山东蓬莱人，2001年于哈尔滨工程大学控制理论与控制工程专业获得博士学位，现为哈尔滨理工大学教授、硕士生导师，主要研究领域为图像处理，机器视觉，模式识别等。发表学术论文70余篇,主持完成了黑龙江省教育厅科研基金项目，承担过多项国家科技攻关项目。

Muhammad Rafique was born in 1989.He is an M.S.candidate at Harbin University of Science and Technology(international student).His research interests include image processing and pattern recognition,etc.

马龙（1989—），男，巴基斯坦人，哈尔滨理工大学硕士研究生（留学生），主要研究领域为图像处理，模式识别等。

LI Ao was born in 1986.He received the Ph.D.degree in communication and information systems from Harbin Engineering University in 2014.Now he is a lecturer at Harbin University of Science and Technology.His research interests include sparse representation,image restoration and computer vision,etc.

李骜（1986—），男，黑龙江哈尔滨人，2014年于哈尔滨工程大学通信与信息系统专业获得博士学位，现为哈尔滨理工大学讲师，主要研究领域为稀疏表示，图像复原，计算机视觉等。主持国家自然科学基金1项、黑龙江省自然科学基金1项，参与船舶工业国防科技预研项目1项，发表学术论文10余篇，授权发明专利1项。

Local Preserving Projection Based on Sample Column Information and Adaptive Neighborhood Graph*

WANG Haiyan,LIN Kezheng+,Muhammad Rafique,LIAo
School of Computer Science and Technology,Harbin University of Science and Technology,Harbin 150080,China

Through introducing the column information of sample,this paper proposes an improved locality preserving projection(LPP)algorithm named adaptive neighbor and corresponding columns of the samples based graph construction method on LPP(ANCCG-LPP)to overcome the defects which parameter k is difficultly selected in traditional k-nearest neighbor graph and the original structure of the image sample is easily ignored by one dimensional vector of the sample for LPP.In the proposed algorithm,corresponding column neighbors of column samples are determined adaptively by the column information of the samples,and then the neighbors of the sample are determined adaptively by the number of coupled column neighbors between two samples.Finally,the optimal projection vectors are solved by redefining the weight matrix to optimize the objective function.Supervised ANCCG-LPP algorithm based on ANCCG-LPP is put forward through adding class information of the samples.The simulation experiments on ORL,Yale Extended B face databases validate the effectiveness of theANCCG-LPP and SANCCG-LPP.

k-nearest neighbor;locality preserving projection;adaptive neighborhood;sample column;structural characteristics

the Ph.D.degree in control theory and control engineering from Harbin Engineering University in 2001.Now he is a professor and M.S.supervisor at Harbin University of Science and Technology.His research interests include image processing,machine vision and pattern recognition,etc.

2016-06, Accepted 2016-10.

A

TP391.4

+Corresponding author:E-mail:link@hrbust.edu.cn

WANG Haiyan,LIN Kezheng,Muhammad Rafique,et al.Local preserving projection based on sample column information and adaptive neighborhood graph.Journal of Frontiers of Computer Science and Technology,2017,11(9)：1474-1483.

10.3778/j.issn.1673-9418.1606030

*The National Natural Science Foundation of China under Grant No.61501147(国家自然科学基金);the Natural Science Foundation of Heilongjiang Province under Grant No.F2015040(黑龙江省自然科学基金).

CNKI网络优先出版: 2016-10-18, http://www.cnki.net/kcms/detail/11.5602.TP.20161018.1622.006.html

摘 要：针对局部保持投影（locality preserving projection，LPP）算法在传统k近邻构图过程中出现的参数k选择困难问题和样本的一维向量容易忽略样本的原始结构特征问题，引入样本的列信息思想，提出了一种基于样本对应列信息的自适应邻域构图的局部保持投影算法（adaptive neighbor and corresponding columns based graph construction on LPP,ANCCG-LPP）。该算法根据样本间的列信息自适应地得出所有样本列的列近邻，然后根据样本间成对的列近邻个数自适应地确定样本的邻域；最后通过重新定义权值矩阵来优化目标函数进行最优投影向量集的求解。在ANCCG-LPP算法的基础上，通过加入样本的类别信息，提出了有监督的ANCCGLPP算法。在ORL、Yale Extended B人脸库上的仿真实验验证了该算法的有效性。