非线性距离的最近邻特征空间嵌入改进方法*
2017-09-18杜弘彦王士同
杜弘彦,王士同
江南大学 数字媒体学院,江苏 无锡 214122
非线性距离的最近邻特征空间嵌入改进方法*
杜弘彦+,王士同
江南大学 数字媒体学院,江苏 无锡 214122
最近邻特征空间嵌入(nearest feature space embedding,NFSE)方法选取最近邻特征空间时使用欧氏距离度量,导致样本的类内离散度和类间离散度同步变化,无法准确反映样本在高维空间的分布;选取每个样本最近邻特征空间都要遍历所有类,导致训练时间长。针对以上问题,提出非线性距离的最近邻特征空间嵌入改进方法(nearest feature space embedding method based on nonlinear distance metric,NDNFSE),引入非线性距离公式选取最近邻特征空间,并使用结合夹角度量的最近邻分类器,提高了识别率;仅在样本的近邻类中选取最近邻特征空间,有效减少了训练时间。实验表明,NDNFSE的训练时间明显低于NFSE,识别率总体高于各对比算法。
人脸识别;非线性距离;夹角;最近邻特征空间嵌入;近邻类
1 引言
在过去的几十年中,模式识别领域的人脸识别越来越为人们所关注,与之相关的技术应运而生,国内外众多学者提出各种算法致力于提高人脸识别的效率和精度,取得了一定的成果。主成分分析(principal components analysis,PCA)[1]方法是一种经典的降维方法,通过线性变换将原始样本映射到低维空间,应用广泛。文献[2]提出的近邻保持嵌入(neighborhood preserving embedding,NPE)方法是无监督降维方法,能够保留局部邻近结构。文献[3]提出的拉普拉斯特征脸方法也可以保留样本的局部结构。拉普拉斯特征映射(Laplacian eigenmaps,LE)[1]和非监督判别投影(unsuperviseddiscriminantprojection,UDP)[4]等方法则可以产生其他非线性流形结构,从而保留样本的局部信息。
无监督的降维算法有时并不能满足所有的应用需要,有监督的算法可以充分利用样本的类标签信息。线性判别分析(linear discriminant analysis,LDA)[5]是最受欢迎的经典的线性降维算法之一,常用于人脸识别。LDA方法利用同类的点到点的向量来计算类内离散度,不同类的点到点的向量计算类间离散度,能够使类间离散度和类内离散度比值最大的判别向量组成最优的转换矩阵,即样本降维的最佳投影方向。LDA是基于整体的学习方法,当样本为线性分布时,收到较好的效果;但当样本不符合线性分布时,则可能难以发现样本的真实结构。
针对上述问题,学者们提出了局部线性嵌入(locally linear embedding,LLE)[6-7]、局部保留投影(locally preserving projection,LPP)[3]、边界费舍尔分析(marginal Fisher analysis,MFA)[8]等基于局部的学习方法。样本的全局非线性结构可视为局部线性,因此LLE通过局部的线性结构来揭示全局的非线性结构。因为缺乏明确的样本投影,所以LLE很难得到测试集中样本点的图像。线性降维方法LPP能够保留样本固有的几何结构,产生适合于训练样本和测试样本的明确线性投影,更适合应用于人脸识别。不过,LPP有着大多数基于流形的学习方法共有的局限性,其目标函数只是最小化局部数量,与分类并不具有直接关系,致使在某些情况下,不能确定生成的是有利于分类的投影矩阵。为了打破LDA和LPP的限制,文献[8]结合LDA与LPP的优势,提出了MFA,使用图嵌入框架,综合样本的局部信息和类别信息来刻画同类样本的紧密程度和异类样本的离散程度,对样本的分布没有特殊要求,应用范围较广。
MFA计算离散度时使用样本点到样本点的向量,文献[9]提出了最近邻特征空间嵌入(nearest feature space embedding,NFSE)方法,借鉴MFA选取类边界样本点参与离散度计算的方法,融入了最近邻特征线(nearest feature line,NFL)[10]匹配方法的思想,以线、面等形成的特征子空间代替单独的点来表示每个类,包含了更多的类别信息,能够更好地表示某个类别的样本,有利于提高分类精度。皋军等多位学者对NFSE进行改进,均取得了一定的成果[11-12]。但是,NFSE在求最近邻特征空间时采用线性的欧氏距离公式进行度量,引起类间离散度和类内离散度同步变化,降低了识别率。作者曾提出基于非线性距离和夹角组合的最近邻特征空间嵌入方法(nearest feature space embedding method based on the combination of nonlinear distance metric and included angle,NL_IANFSE),引入非线性距离公式计算样本点到特征空间的距离,保证类内距离的变化速率远小于类间距离变化速率,使得类间离散度与类内离散度的比值增大,得到判别力更强的投影矩阵;另外,NL_IANFSE在测试阶段使用结合夹角度量的最近邻分类器代替传统的最近邻(nearest neighbor,NN)分类器,将不同样本的相似性和它们的位置关系都纳入考虑范围,最终得到了比NFSE更高的识别率。
NFL匹配规则可用于人脸识别的测试阶段,将NN中求两个样本点之间的距离改为求样本点到它在特征线上投影点的距离,分类效果比NN好,但所花费时间却更长。NL_IANFSE和NFSE都是把NFL通过判别分析嵌入到转换过程中,相当于把求特征点到特征子空间距离的计算从测试阶段转移到训练阶段,故二者的训练时间都较长。
为了降低NL_IANFSE训练阶段的时间复杂度,本文借用文献[13]提出的加强的边界费舍尔分析(enhanced marginal Fisher analysis,EMFA)的思想,先通过比较某样本点所在类的类中心与其他类中心的距离,选出若干个近邻的类,然后再计算这个样本点到近邻类的各个特征子空间的距离,并分别取出每个类中相同数目的最小距离参与类间离散度的计算。这样做有效避免了求样本点到其他类别的特征子空间距离时遍历训练集中所有类别的做法,节省了大量的时间。实验表明,采用这种方法,在大幅度提升训练效率的情况下仍能得到和NL_IANFSE相当的分类准确率。
2 相关研究
2.1 最近邻特征空间嵌入
最近邻特征空间嵌入方法综合前人算法的优点,利用LPP方法保留局部结构,将最近邻特征空间度量、邻近结构保留和分类相结合。用每一类中若干个特征点线性结合形成的特征子空间来分别表示各个类,依次求出每个样本点到同类和不同类特征子空间的向量,根据向量长度排序,取出同类特征子空间中前K1个长度最短的向量和不同类特征子空间中前K2个长度最短的向量。在计算离散度时,借助拉普拉斯矩阵来简化计算,然后最大化Fisher准则以得到最优转换矩阵。
2.2 基于非线性距离和夹角组合的最近邻特征空间嵌入方法
NL_IANFSE在NFSE的基础上,引入非线性距离公式选取最近邻特征空间,使得类间离散度的变化速度远大于类内离散度的变化速度,从而嵌入空间中同类样本更为接近,不同类样本相距较远,更便于分类。另外,针对传统最近邻分类器只考虑样本间直线距离而无法如实反映高维空间中样本分布的问题,NL_IANFSE使用结合夹角度量的分类器,提高了最终识别率。
2.2.1 非线性距离计算公式
有监督的局部线性嵌入(supervised locally linear embedding,SLLE)[14]算法中加入样本类别信息构造邻域。文献[15]对构造邻域时用到的距离公式进行改进,提出非线性距离公式。设xi、xj为两个样本点,二者之间的非线性距离计算公式可写作:

其中,A是xi、xj两个样本点间的欧氏距离;B是所有样本点两两之间的欧式距离的均值;α是一个属于[0,1]区间的参数,表示样本点类别信息的结合程度,调节不同类的样本之间的距离。
2.2.2 结合夹角度量的最邻近分类器
由于样本间的相似性越大,其夹角越小,而同类样本间的相似性要比异类样本间的相似性更大,通过样本间夹角大小来辅助判断两个样本类标签是否相同是可行的。文献[16]将样本两两之间的夹角和其直线距离相结合,得到结合夹角度量的最近邻分类器。相比最近邻分类器,结合夹角度量的最近邻分类器的优点在于,当高维空间中样本间直线距离趋同时,可以凭借夹角的大小反映样本分布情况,更适合高维数据分类。
首先,通过余弦定理求出两个高维空间样本xi和xj的夹角:

然后,通过以下公式计算得到关于xi、xj的融合值:

其中,β∈[0,1],是融合系数;Di·表示 xi和其他所有样本点的直线距离;θi·表示xi和其他所有样本点的夹角。与xi融合后取得最小值的样本所属的类即是xi所属的类。
2.3 加强的边界费舍尔分析
传统的边界费舍尔分析用k1和k2两个参数分别控制类内样本的紧密度和类间样本的分散度,其中k1表示距离样本xi最近的与xi同类的样本点的个数,k2表示距离xi最近的位于其他类边界的样本点的个数。参数k2的确定对于正确划分不同类样本至关重要。假设训练集共有N个类,传统的MFA在选取xi到其他类的最近邻样本时,遍历除xi所在类之外的N-1个类,求出xi到这些类中每个样本点的距离,将这些距离按照从小到大的顺序排列,取出前k2个到xi距离最小的样本点参与后续的类间离散度矩阵的计算。
这样做可能带来两个问题:第一,求每个样本的类间近邻点都遍历N-1个类会耗费大量的时间,降低算法效率。第二,直接从所有与xi不同类的样本点中选择前k2个到xi距离最小的样本点,可能漏掉某些类的边界点,导致边界点选取有误差,不利于投影空间中的样本分类。
因此,文献[13]提出加强的边界费舍尔分析。首先求出各类的类均值和xi所在类与其他类的距离,然后选出距离最小亦即最接近xi所在类的Ne个类。依次计算xi到Ne个类中每个类的所有样本的直线距离,从每个类中选取距离最小的Ke个样本点,共计Ne×Ke个样本点。用得到的Ne×Ke个样本点代替传统MFA选取的k2个类间近邻点参与类间离散度的计算。如图1所示,Ne=2,Ke=3,第B类样本集和第C类样本集是第A类样本集的最近邻样本集,B、C中的到xi最近的边界点用连线标出。
3 非线性距离的最近邻特征空间嵌入改进方法
NFSE和NL_IANFSE在训练阶段,计算类间离散度之前寻找每个训练样本的不同类的最近邻特征子空间,需要遍历训练集的所有类,耗费大量的时间。为提高效率,本文引入EMFA先求近邻类再取边界点的思想,提出了非线性距离的最近邻特征空间嵌入改进方法(nearest feature space embedding method based on nonlinear distance metric,NDNFSE),在求类间最近邻特征子空间之前先求出xi所在类的近邻类,然后只遍历这些邻近类中的特征子空间,计算其到xi的距离,最后排序取出距离xi最近的特征子空间。这样做有效减少了训练时间,同时能够保证识别率比NFSE高,和NL_IANFSE基本持平。下文将对此方法进行详细介绍。

Fig.1 Selecting marginal points of one sample图1 选取某样本类边界点
3.1 寻找每个类的近邻类
减少训练时间的关键是仅从xi所在类的近邻类中选取边界点,而不再要求每次取训练样本边界点时都遍历所有类。因此,通过以下方法先求出每个类的邻近类。假设训练集共有Nc个类,每类有mi(i=1,2,…,Nc)个样本。Xi(i=1,2,…,Nc)表示训练集中第i类的样本集,每类样本的平均向量即均值用vi(i=1,2,…,Nc)表示,计算类均值的公式如下:

求出各类均值后,利用这些均值两两之间的欧氏距离表示每类样本集之间的中心距离,以此来衡量类与类之间的远近。如以下公式所示,用q表示某类的中心,Cab表示第a类和第b类样本集的类中心距离的平方:

其中,a,b∈{1,2,…,Nc},a≠b。φi={Xri|i=1,2,…,Nc,r=1,2,…,Ne}表示与第 i个类近邻的Ne个类,如果Xr∈φi,则可以认为第r个类的样本接近于第i个类的样本,即第r个类是第i个类的近邻类。
3.2 选取样本点的近邻特征子空间
特征线比特征点包含更多的信息,能够更好地表示类,文献[10]使用一类中两个样本点线性组合形成的特征线来表示该类样本,提出了一种更利于样本分类的最近线性组合的分类器。假设每个类中有mi(i=1,2,…,Nc)个样本,每个子空间由Q个样本点生成,此时第i个类总共可以产生个特征子空间。当Q=1时,特征子空间为一个特征点;当Q=2时,特征子空间为一条特征线;当Q=3时,特征子空间为一个特征面;进而可推广至Q>3。由于没有证据表明,当Q≥3时NFSE算法最终的分类效果更佳,故本文只讨论Q=2时的情况。为第i类的第j个样本,设xm、xn为不同于的两个同类样本点,通过xm、xn的直线即为xm、xn所在类的特征线,的投影点记为p(2)(xji),可以用xm、xn的线性组合表示为,根据文献[10],。
3.3 转换矩阵
人脸识别算法中时常用到Fisher准则,这是利用了类别信息的判别准则函数,定义为类间离散度和类内离散度的比,通过最大化这个比值得到优化的判别投影轴,使得样本投影到投影空间后不同类样本间距离较大,同类样本间距离较小,更容易进行分类。由3.2节得到集合,用以计算类内离散度矩阵和类间离散度矩阵。取Q=2,假设经过yi=wTxi转换后的低维空间中的样本集合为T={y1,y2,…,yN},T中的样本点两两之间共可产生个特征子空间,即条特征线,用 p(2)表示。样本点yi到特征线的投影点表示为p(2)(yi),yi到特征线的向量yi-p(2)(yi)用ym和yn表示,共有个向量,公式推导如下:
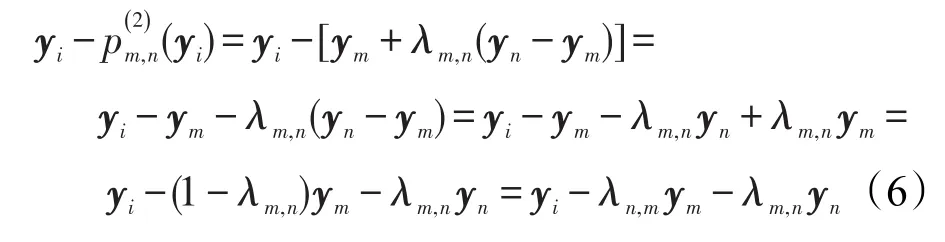
其中,λm,n、λn,m是低维空间中的权重,满足条件λm,n+λn,m=1。
计算离散度矩阵的公式如下:
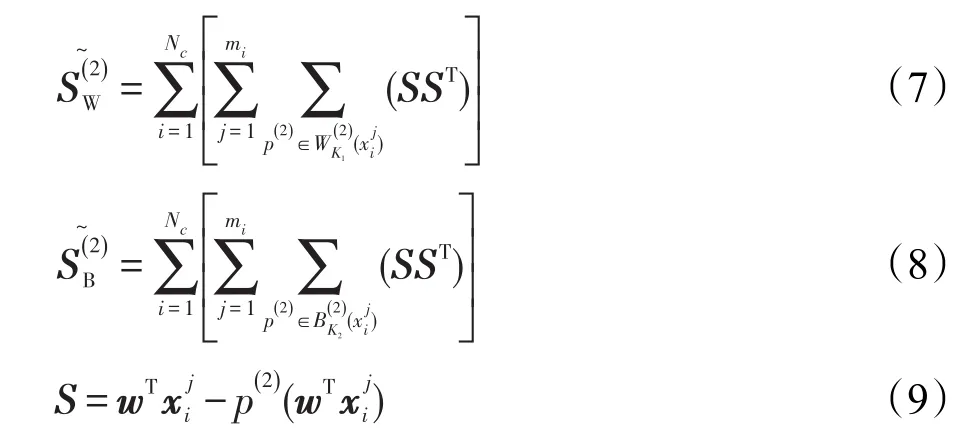
找出样本点yi到最近的K个特征子空间的判别向量进行判别分析,向量yi-p(2)(yi)的长度为||yig(2)(yi)||,写出NDNFSE的目标函数,当此目标函数取得最小值时,线性变换yi=wTxi中的w即为所求的转换矩阵。

其中,权值矩阵ω(2)(yi)表示N个特征点和它们对应的投影点之间的连接关系。
目标函数F可以看作由K个部分组成,分别为各个样本点到第K近的特征线的距离的平方和,逐步推导成便于计算的拉普拉斯矩阵的形式。
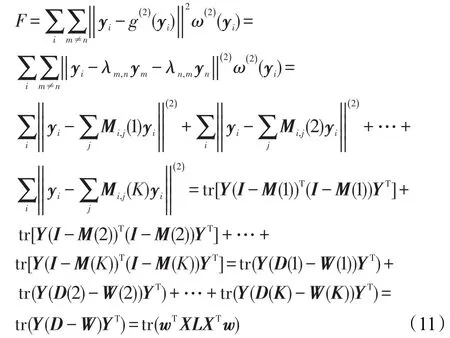
式中,Mi,j(K)是一个稀疏矩阵,表示yi和距离它第K近的特征线的连接关系。M的每一行有且只有两个相加和为1的非零值。例如,Mi,j(1)是yi和最近邻特征线的连接关系矩阵,i≠m≠n。Mi,m(1)=λn,m,Mi,n(1)=λm,n,并且满足 Mi,m(1)+Mi,n(1)=1,Mi,j(1)中第 i行的其他列元素均为0。同理,Mi,j(2)是yi和第二近的特征线的连接关系矩阵,Mi,m(2)=λn,m,。
依此类推。当i=j时,Wi,j(K)=(M(K)+M(K)T-M(K)TM(K))i,j,当 i≠j时,Wi,j(K)=0。另外,D=(D(1)+D(2)+…+D(K))/K,W=(W(1)+W(2)+…+W(K))/K。
根据矩阵的迹的性质||S||2=SST,离散度矩阵可以化简成拉普拉斯矩阵的形式:
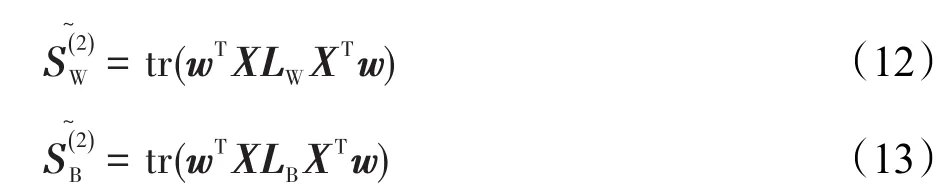
其中,LW=DW-WW表示类内的情况,LB=DB-WB表示类间的情况。
求出类内离散度和类间离散度的表达式后,最大化Fisher准则得到转换矩阵。
3.4 NDNFSE算法步骤
结合以上叙述,总结出NDNFSE的算法步骤如下。
输入:N 个训练样本 s1,s2,…,sN,参数 R、K1、K2、Ke、Ne、α、β、r。
输出:转换矩阵w=wPCAw*。
步骤1每个训练样本为一个列向量,通过PCA算法将训练样本降到R维,使样本维数小于样本总数,从而避免小样本问题。由此得到第一个转换矩阵wPCA和降维后的训练样本xi=wPCAsi,i=1,2,…,N。
步骤2 通过式(4)、(5)求出 xi所在类的 Ne个近邻类。
步骤3求出xi在特征空间中的投影点p(2)(xi),i=1,2,…,N。对于每个样本点,依据式(1)计算其到类内特征子空间的距离,并按照距离大小排序,选出K1个最近邻特征空间;再求出xi到Ne个近邻类的特征子空间的距离,在Ne个类的每类中都选出距离xi最近的 Ke个特征空间,共 Ke×Ne个,记 K2=Ke×Ne。
步骤4根据式(7)、(8)计算类内离散度和类间离散度。
步骤5最大化Fisher得到第二个转换矩阵w*=。取最大的r个特征值对应的特征向量组成w*。
步骤6得到最终的转换矩阵w=wPCAw*。
步骤7通过w将测试集也投影到低维空间,利用式(3)判断测试样本所属类别。
3.5 NDNFSE算法效率分析
在训练阶段,计算样本的类间离散度之前需要选出每个训练样本在不同类样本中的K2个最近邻特征空间。因此,NFSE算法依次求出各样本到Nc-1个类中所有特征子空间的距离,亦即到特征子空间的投影点的欧氏距离,将得到的个距离进行排序,取最小的前K2个。NL_IANFSE方法在这一步需要计算的距离数目与NFSE相等,但它采用非线性距离度量,根据式(1)的参数要求,预先遍历所有类,计算所有训练样本到各个类的特征子空间的欧氏距离之和,取其均值作为式(1)的参数B。NDNFSE方法同样使用了非线性距离公式,但改变了NFSE遍历所有类寻找最近邻特征子空间的做法,先通过计算每类样本中心及类中心两两之间的距离求出每类样本的Ne个近邻类,求每个样本的类间最近邻特征子空间时,只要计算每个样本到所在类的这Ne个近邻类中特征子空间的个非线性距离即可。当数据集的类别数较多时,控制Ne的取值,可以使NDNFSE的训练时间远远小于NFSE和NL_IANFSE算法的训练时间。
在测试阶段,NFSE使用传统的最近邻匹配方法,依次求出每个测试样本到各训练样本的欧氏距离,将距离最近的训练样本的类标作为预测的结果。设每类有mi个训练样本,则对于一个测试样本,需计算Nc×mi个距离。NL_IANFSE和NDNFSE使用结合夹角的最近邻分类器,除了计算测试样本到训练样本的欧氏距离外,还要利用式(2)求测试样本与训练样本之间的夹角,并进而通过式(3)得到样本间的融合值,所需时间较长。
4 实验设计及结果分析
4.1 数据集与实验设计
本文使用Yale B、ORL、CMU PIE[17]和AR共4个人脸数据集进行实验。Yale B数据集是耶鲁大学建立的,由10位志愿者的面部图像组成,每人585幅,实验选用其中的640幅图像,每人64幅。由剑桥大学创建的ORL人脸数据集采集了40位志愿者的图像,每人10张表情不同的正面照,总共400张。CMU PIE数据集包含68名志愿者在不同的姿势、光照、表情下的面部图像,共有4万多张,本文选用了其中67人的照片,每人170张。AR数据集由西班牙巴塞罗那计算机视觉中心创建,本文使用120名志愿者的面部图像,每人26幅。
实验之前需要进行图像的归一化处理,减少背景和头发对识别的影响,将每幅图像裁剪成32×32像素大小的灰度图像。每类随机抽出一定数目的样本组成训练集,其余作为测试集,再使用PCA算法将原始训练集降到R维(R小于训练样本数N)以避免小样本问题。用随机选取的方式分别将每个数据集以不同比例划分为训练集和测试集,观察训练样本的数量对识别率和训练时间的影响。
按照经验,式(1)中的参数 α设为0.5,式(3)中结合夹角度量的最近邻分类器中的融合参数 β设为0.2。为了研究最终转换空间维数对识别率的影响,对于转换矩阵w*的维数r,实验取5至80之间的不同值。
实验着重对比了K2取不同值时,NDNFSE识别率和训练时间的变化。相应地,对NDNFSE中的参数Ne和Ke进行调整,比较当选取的不同类最近邻特征空间数目大约相同时,NDNFSE和NFSE、NL_IANFSE的识别率及训练时间。
实验中的对比算法包括PCA+LPP[3]、PCA[1]、PCA+LDA[5]、PCA+NPE[2]、PCA+NFSE[9]以及 PCA+NL_IANFSE。在测试阶段,PCA+LPP、PCA、PCA+LDA、PCA+NPE、PCA+NFSE用NN规则,也就是最近邻分类器来匹配,NL_IANFSE和NDNFSE则使用结合夹角度量的最近邻分类器。下文列出的每个识别率都是分别在相同条件下运行10次后求取的平均值。
实验平台:上述4个数据集均在Intel Core i3-3240×2CPU的Windows操作系统的计算机上进行实验,主频为3.4 GHz,内存为4 GB,编程环境为Matlab R2015a。
4.2 实验结果与分析
将实验所得数据整理归纳,用图、表的形式表示。下面按数据集归类展示结果,并进行必要的描述和分析。
4.2.1 Yale B数据集
从Yale B数据集的每类中随机抽取一定数量的样本用于训练,其余留作测试集,并通过PCA算法将训练集降到100维,每个训练样本的类内最近邻特征空间的个数 K1设为10,Ne依次设为3、6、9,Ke设为3,于是每个训练样本的不同类最近邻特征空间依次取9、18、27个。表1列出了NDNFSE、NL_IANFSE和N FSE在每类训练样本数分别为10和15个,K2值不同时的最高识别率、标准差和相应的转换空间维数,以及运行1次平均需要花费的训练时间。
由表1得,在参数K2相近时,NDNFSE在5到80维的最高识别率均明显高于NFSE的最高识别率,略高于NL_IANFSE;NDNFSE单次运行所花的训练时间均少于NL_IANFSE和NFSE的训练时间。
表2列出了各算法的最高和最低识别率及所在维数、标准差,图2则描绘了在NDNFSE方法K2=27,NFSE方法K2=30时,各算法在不同维数投影空间的识别率。可以看出,NDNFSE在各个维数的识别率几乎都要高于对比算法,标准差也较低,说明NDNFSE较为稳定。

Table 1 Recognition rates and training time on Yale B database表1 Yale B数据集上的识别率和训练时间
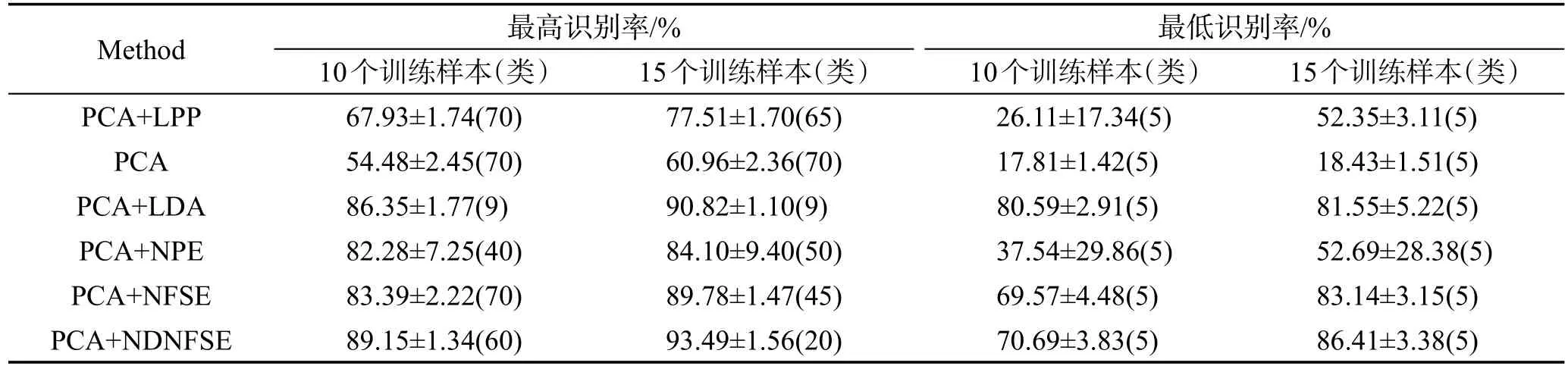
Table 2 The highest and the lowest recognition rates,standard derivations on Yale B database表2 Yale B数据集上的最高识别率、最低识别率及标准差

Fig.2 Recognition rates versus dimensionality reduction with various training samples on Yale B database图2 各算法将Yale B数据集降到不同维数时的识别率
4.2.2 ORL数据集
当ORL数据集每类任取4个样本组成训练集时,用PCA算法降至120维,设K1=3;当每类任取5个样本进行训练时,训练集用PCA算法降至160维,设K1=6。NDNFSE中参数Ne,即每类样本的近邻类的数目,分别取10、15、20,参数 Ke都取3。在 K2值分别不同的条件下,NDNFSE、NL_IANFSE和NFSE最高识别率、训练时间等对比如表3所示。
根据实验结果可知,在参数相同的情况下,NDNFSE用更短的训练时间达到了和NL_IANFSE、NFSE几乎相当的最高识别率,尤其当K2值为60的时候NDNFSE的识别率比NFSE高1.96%,但所用的训练时间只有NFSE的66.1%。
NDNFSE与NFSE的参数K2都设为60时,NDNFSE与对比算法的最高识别率、最低识别率如表4所示。从中可知,NDNFSE的最高识别率高于各对比算法,最低识别率虽然低于某些对比算法,但比NFSE稍高。
4.2.3CMU数据集
PCA算法将CMU训练集降到300维,设K1为10,Ke为1。表5列出了训练集每类9个、14个样本时NDNFSE、NL_IANFSE、NFSE在不同K2值的最高识别率和训练时间。可见,当K2值相等时,NDNFSE的最高识别率与NL_IANFSE基本持平,比NFSE高出5%左右,而训练时间要远远少于NL_IANFSE和NFSE。
图3画出了NDNFSE与对比算法在5~70维的识别率变化曲线,NDNFSE及NFSE均设 K2为30。NDNFSE在各维度的识别率都优于对比算法,在较高维度表现出更明显的优势。随着维数的增大,识别率稳步提升,逐渐趋于稳定。
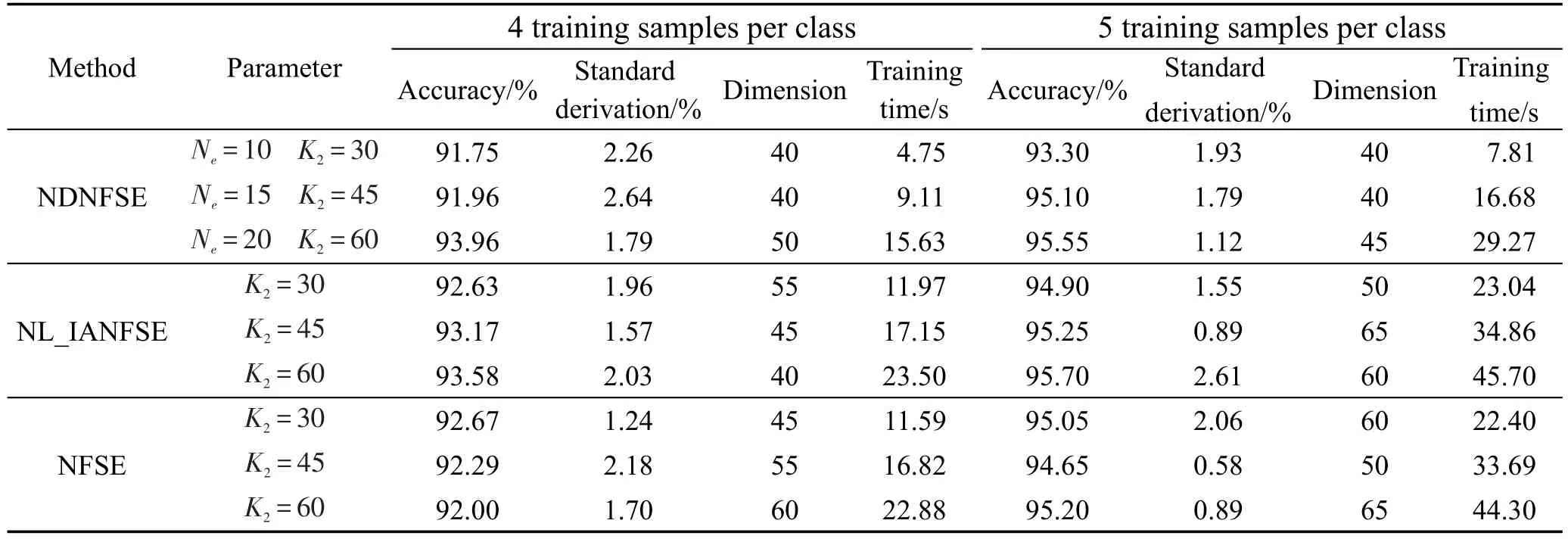
Table 3 Recognition rates and training time on ORL database表3 ORL数据集上的识别率及训练时间
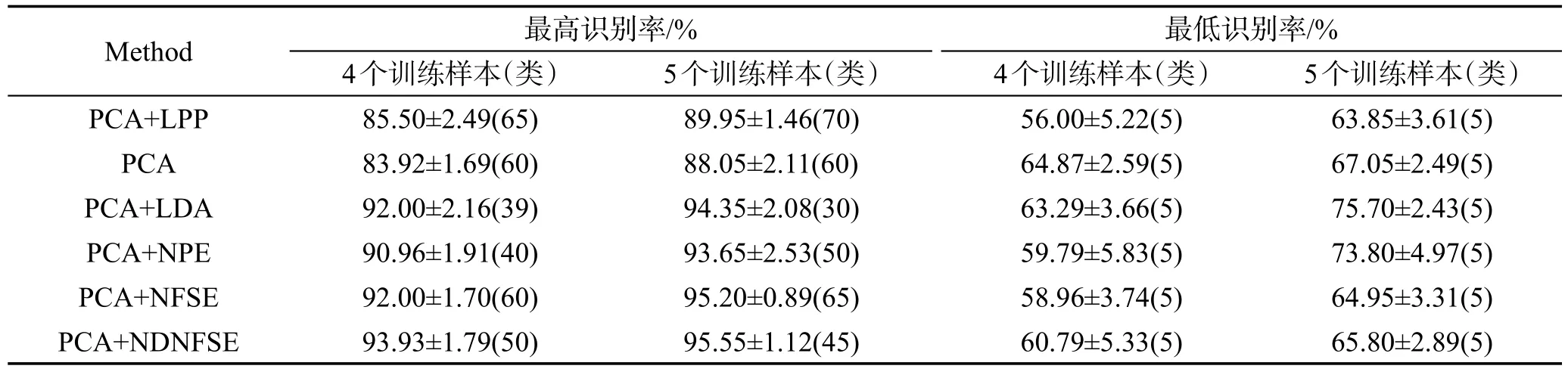
Table 4 The highest and the lowest recognition rates,standard derivations on ORL database表4 ORL数据集上的最高识别率、最低识别率及标准差

Table 5 Recognition rates and training time on CMU database表5 CMU数据集上的识别率及训练时间

Fig.3 Recognition rates versus dimensionality reduction with various training samples on CMU database图3 各算法将CMU数据集降到不同维数时的识别率
4.2.4 AR数据集
与CMU数据集相同,AR数据集的训练集通过PCA算法降到300维,Ke=1。每类4个训练样本时K1=3,每类6个训练样本时K1=6。
NDNFSE、NL_IANFSE和NFSE在不同参数条件下的最高识别率和训练时间如表6所示。表7是K2=30时NDNFSE与对比算法在各维度投影空间的最高和最低识别率。NDNFSE的最高识别率几乎高于所有对比算法,而且训练时间只有NL_IANFSE和NFSE的1/6到1/3。
4.2.5 测试时间
根据3.5节中对测试方法的分析可知,NFSE、NL_IANFSE和NDNFSE的测试时间与K1、K2取值无关,只与训练集、测试集的划分比例有关。表8列出了Yale B、ORL、CMU和AR数据集上的参数设置,以及在不同参数设置下3种算法求出单个测试样本类别所用的测试时间。
NL_IANFSE和NDNFSE使用的结合夹角度量的最近邻分类器比NFSE使用的传统最近邻分类器更复杂,对于每一个测试样本,都需要求出其与所有训练样本的直线距离及夹角,并分别计算距离和夹角的最大、最小值,最后得出待测试样本与训练样本的融合值。因此,当训练样本数目越大时,所需的测试时间越长。

Table 6 Recognition rates and training time onAR database表6 AR数据集上的识别率及训练时间
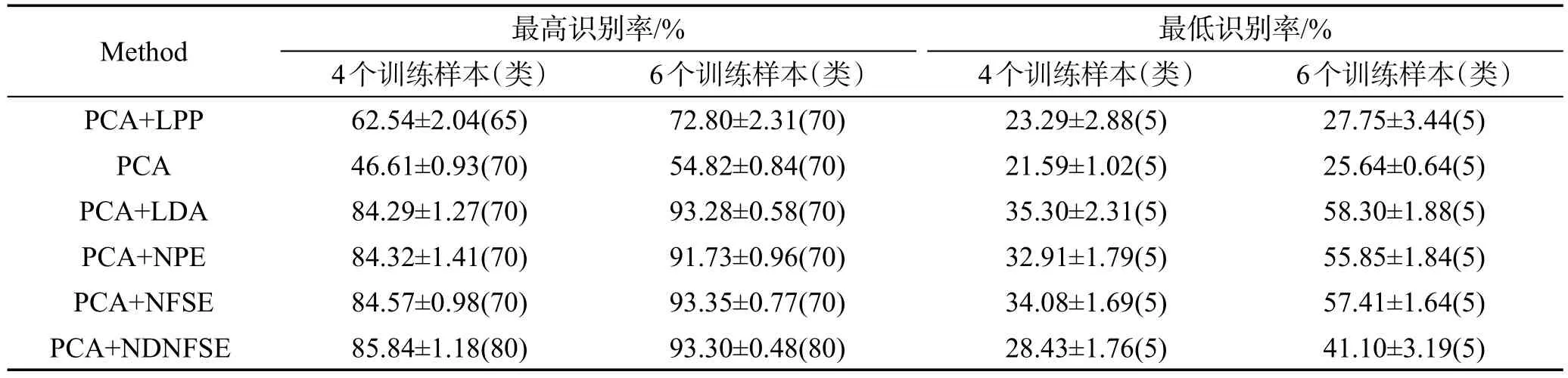
Table 7 The highest and the lowest recognition rates,standard derivations onAR database表7 AR数据集上的最高识别率、最低识别率及标准差
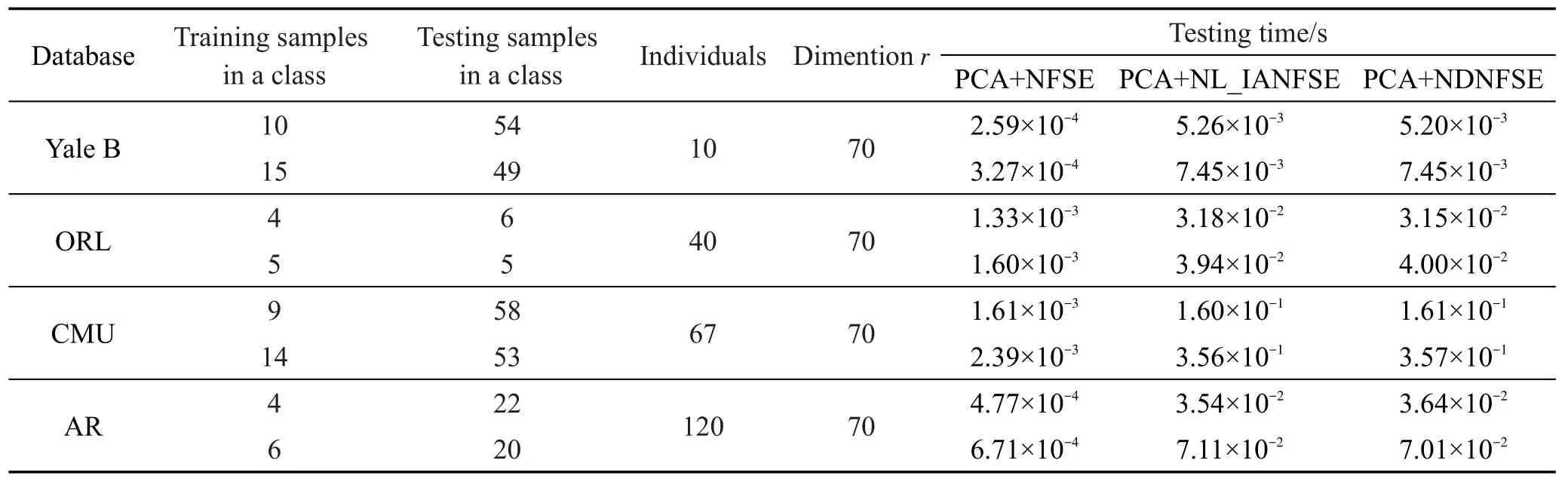
Table 8 Testing time of single sample algorithms spending on 4 databases表8 在4个数据集上求出单个测试样本类别所需时间
由表8可以看出,Yale B、ORL数据集上各算法的测试时间差距不是很大,训练样本数较多的CMU和AR数据集上,NL_IANFSE和NDNFSE的测试时间明显比NFSE长。
根据以上4个数据集的实验结果,可以归纳出以下几点:
(1)当K2值相等或接近时,NDNFSE的最高识别率与NL_IANFSE相差很小,基本在1%以内,在Yale B和CMU这两个数据集上比NFSE高5%左右;
(2)NDNFSE运行一次的训练时间要比NL_IANFSE和NFSE大幅度减少;
(3)在除ORL数据集之外的3个数据集的实验中,没有发现NDNFSE得到的识别率随K2的增大而提高,但是却发现训练时间随K2的增大而迅速增加;
(4)随着每类训练样本数和样本维数的增加,样本信息增加,各算法识别率有不同程度提高;
(5)在4个数据集的实验中,NDNFSE的标准差大多在1%上下,性能比较稳定;
(6)NDNFSE 与 PCA+LPP、PCA、PCA+LDA、PCA+NPE等经典算法相比也具有一定的优势;
(7)由于分类器不同,NDNFSE和NL_IANFSE的测试时间比NFSE长,并且数据集中训练样本数越多,测试时间越长。
5 结束语
本文以NFSE算法为基础,结合非线性距离公式[14]和结合夹角度量的最近邻分类器[17],在一定程度上解决了高维空间中样本欧氏距离无法准确描述样本分布的问题,在匹配时充分利用样本间相似性与其夹角的关系,达到提高识别率的目的。引入文献[13]中先求近邻类再选取边界点的方法,避免了寻找每个样本的类间最近邻特征空间时都要遍历所有类的样本,节省了大量训练时间。实验表明,较之NL_IANFSE、NFSE,NDNFSE单次运行的训练时间明显大幅减少,同时能够保持识别率与NL_IANFSE基本相当,比NFSE等5个经典算法更高。NDNFSE的不足之处是测试阶段花费时间比NFSE长,今后工作中需要寻找效率更高的匹配方法。
[1]Turk M A,Pentland A P.Face recognition using eigenfaces[C]//Proceedings of the 1991 Computer Society Conference on Computer Vision and Pattern Recognition,Maui,USA,Jun 3-6,1991.Piscataway,USA:IEEE,1991:586-591.
[2]He Xiaofei,Cai Deng,Yan Shuicheng,et al.Neighborhood preserving embedding[C]//Proceedings of the 10th International Conference on Computer Vision,Beijing,Oct 17-21,2005.Washington:IEEE Computer Society,2005:1208-1213.[3]He Xiaofei,Yan Shuicheng,Hu Yuxiao,et al.Face recognition using Laplacian faces[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2005,27(3):328-340.
[4]Zhang Taiping,Fang Bin,Tang Yuanyan,et al.Topology preserving non-negative matrix factorization for face recognition[J].IEEE Transactions on Image Processing,2008,17(4):574-584.
[5]Belhumeur P N,Hespanha J P,Kriegman D J.Eigenfaces vs.Fisherfaces:recognition using class specific linear projection[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2007,19(7):711-720.
[6]Roweis S T,Saul L K.Nonlinear dimensionality reduction by locally linear embedding[J].Science,2000,290(22):2323-2326.
[7]Saul L K,Roweis S T.Think globally,fit locally:unsupervised learning of low dimensional manifolds[J].Journal of Machine Learning Research,2003,4(2):119-155.
[8]Yan Shuicheng,Xu Dong,Zhang Benyu,et al.Graph embedding and extensions:general framework for dimensionality reduction[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2007,29(1):40-51.
[9]Chen Y N,Han C C,Wang C T,et al.Face recognition using nearest feature space Embedding[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2011,33(6):1073-1086.
[10]Li S Z,Lu Juwei.Face recognition using the nearest feature line method[J].IEEE Transactions on Neural Networks,1999,10(2):439-433.
[11]Gao Jun,Huang Lili,Wang Shitong.Local sub-domains based maximum margin criterion[J].Control and Decision,2014,29(5):827-832.
[12]Chen Y N,Ho G F,Fan K C,et al.Orthogonal nearest neighbor feature space embedding[C]//Proceedings of the 8th International Conference on Intelligent Information Hiding and Multimedia Signal Processing,Piraeus-Athens,Greece,Jul 18-20,2012.Piscataway,USA:IEEE,2012:166-169.
[13]Huang Pu,Chen Caikou.Enhanced marginal Fisher analysis for face recognition[C]//Proceedings of the 2009 International Conference on Artificial Intelligence and Computational Intelligence,Shanghai,Nov 7-8,2009.Washington:IEEE Computer Society,2009:403-407.
[14]Ridder D D,Kouropteva O,Okun O,et al.Supervised locally linear embedding[C]//LNCS 2714:Proceedings of the 2003 Joint International Conference on Artificial Neural Net-works and Neural Information Processing,Istanbul,Turkey,Jun 26-29,2003.Berlin,Heidelberg:Springer,2003:333-341.
[15]Zhang Shiqing,Li Lemin,Zhao Zhijin.Speech emotion recognition based on an improved supervised manifold learning algorithm[J].Journal of Electronics&Information Technology,2010,32(11):2724-2729.
[16]Liu Jiamin,Luo Fulin,Huang Hong,et al.Locally linear embedding algorithm based on fusion angle measurement[J].Opto-Electronic Engineering,2013,40(6):97-105.
[17]Sim T,Baker S,Bsat M.The CMU pose,illumination,and expression database[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2003,25(12):1615-1618.
附中文参考文献:
[11]皋军,黄丽莉,王士同.基于局部子域的最大间距判别分析[J].控制与决策,2014,29(5):827-832.
[15]张石清,李乐民,赵知劲.基于一种改进的监督流形学习算法的语音情感识别[J].电子与信息学报,2010,32(11):2724-2729.
[16]刘嘉敏,罗甫林,黄鸿,等.融合夹角度量的局部线性嵌入算法[J].光电工程,2013,40(6):97-105.

DU Hongyan was born in 1990.She is an M.S.candidate at Jiangnan University.Her research interests include artificial intelligence and pattern recognition.
杜弘彦(1990—),女,山西太原人,江南大学硕士研究生,主要研究领域为人工智能,模式识别。

WANG Shitong was born in 1964.He is a professor and Ph.D.supervisor at Jiangnan University.His research interests include artificial intelligence,pattern recognition,image processing and application.
王士同(1964—),男,江苏扬州人,江南大学教授、博士生导师,主要研究领域为人工智能,模式识别,图像处理及应用。
Nearest Feature Space Embedding Method Based on Nonlinear Distance Metric*
DU Hongyan+,WANG Shitong
College of Digital Media,Jiangnan University,Wuxi,Jiangsu 214122,China
Nearest feature space embedding(NFSE)method uses traditional Euclidean distance measure to select the nearest feature spaces,which causes within-class scatters and between-class scatters changing synchronously and cannot reflect the distribution of samples in the higher dimensional space accurately.Traversing all the classes when selecting the nearest feature space classes of every sample makes the training time long.To solve above problems,this paper proposes the nearest feature space embedding method based on nonlinear distance metric(NDNFSE),by using nonlinear distance formula to select the nearest feature spaces and using the nearest neighbor classifier combined with Euclidean distance and included angle between two samples to improve the recognition rate.NDNFSE only selects the nearest feature spaces within the nearest classes of every sample to save the training time.According to the experimental results,NDNFSE outperforms comparison algorithms for classification as a whole,with much shorter training time than that of NFSE.
face recognition;nonlinear distance;included angle;nearest feature space embedding;nearest classes
2017-03, Accepted 2017-05.
A
TP181
+Corresponding author:E-mail:18800585201@163.com
DU Hongyan,WANG Shitong.Nearest feature space embedding method based on nonlinear distance metric.Journal of Frontiers of Computer Science and Technology,2017,11(9):1461-1473.
10.3778/j.issn.1673-9418.1703034
*The National Natural Science Foundation of China under Grant No.61272210(国家自然科学基金).
CNKI网络优先出版: 2017-05-16, http://kns.cnki.net/kcms/detail/11.5602.TP.20170516.1306.002.html
