平原感潮地区雨型潮型组合对除涝规模的影响

季永兴,刘水芹

(1.上海市水利工程设计研究院有限公司,上海 200061; 2.上海市水务局防汛减灾工程技术研究中心,上海 200061;3.上海市水文总站,上海 200332)

平原感潮地区雨型潮型组合对除涝规模的影响

季永兴1,2,刘水芹3

(1.上海市水利工程设计研究院有限公司,上海 200061; 2.上海市水务局防汛减灾工程技术研究中心,上海 200061;3.上海市水文总站,上海 200332)

以上海某感潮圩区水系除涝规模计算为例,采用水量平衡法和河网水动力数学模型法,研究了平原感潮地区的雨型潮型组合对圩区除涝规模的影响,并对涉及除涝标准的暴雨历时取值、涝水排除程度确定、起调水位与预降可能性、河道分期实施状况、用地性质变化、水面率控制等影响因素进行了分析。结果表明:在约100 km2区域内,采用水量平衡法和河网水动力数学模型法计算的河道水力要素和除涝设施规模均可满足工程精度要求;对确定的除涝规模,不同雨型潮型组合情况下,内河最高水位和高水位持续时间不同,“麦莎”雨型潮型组合情况下内河最高水位较高,而“63年”雨型潮型组合情况下高水位持续时间较长,后期河道水位也较高;平原感潮圩区除涝标准的确定涉及设计暴雨重现期、设计暴雨历时、涝水排除时间、涝水排除程度、设计潮位与过程等因素,尤其是雨型潮型组合对除涝规模影响较大。

平原感潮地区;圩区;雨型潮型组合;除涝标准;除涝规模

为适应社会经济发展需要,缓解人口增长对土地需求的压力,保持耕地动态平衡,我国沿海各省利用滩涂资源建设了大量的围海造地工程,如河北曹妃甸[1]、江苏沿海[2]、上海浦东机场[3]、浙江温州浅滩[4]、福建东壁岛[5]等围海造地工程。位于沿海的新围区域,成陆高程较低,有海堤保护,围区除涝排水有其共同特点:外海高潮位时,围区内水难以排出,需要泵站强排;外海低潮位时,围区内水又可自流外排。新围区域的圩区排水既可建成独立排水体系,又可与内陆水系合并排水。与内陆水系合并的围区,其排水系统(包括河道与口门控制建筑物等)需综合考虑原排水范围及新围区的上游来水与本地区降雨;独立排水体系的新围区一般仅考虑本区域降雨。但是,不管是否与内陆水系合并排水,新围区域排水系统的水系河道规模及口门控制建筑物的规模,均与降雨、潮位组合关系密切,属于典型的平原感潮区排水除涝问题。

2016年1月水利部颁布的SL 723—2016《治涝标准》规定了除涝标准“应同时以设计暴雨重现期、设计暴雨历时、涝水排除时间和涝水排除程度等指标表示”,但相关研究表明,设计暴雨过程(雨型)与设计潮位过程(潮型)组合对感潮区除涝规模影响较大[6-9]。在上海,水利部门以往采用典型年法来解决雨型潮型组合时除涝规模的影响问题,即采用1963年9月12—13日24 h降雨(总降雨量204.6 mm,相当于20年一遇降雨标准,其中1 h最大降雨36 mm)与同步的外海潮位进行组合(简称“63年”雨型潮型组合)。2005年8月6—7日,“麦莎”台风期出现了台风、暴雨、高潮“三碰头”情况[10](总降雨量为198.9 mm,也接近20年一遇降雨量,其中1 h最大降雨49 mm),许多区域出现内涝,相关部门和学者开始着手研究原“63年”雨型潮型组合的可靠性、采用“麦莎”台风期间雨型潮型组合(简称“麦莎”雨型潮型组合)的可行性[11]以及其他雨型潮型组合的合理性。

由于雨型潮型组合确定最终是为确定水系河道规模和口门控制建筑物规模服务的,本文以上海某圈围成陆总面积约87.9 km2的围海造地工程内的除涝规划设计为例,对雨型潮型组合对水系河道规模确定的影响进行分析,并对平原感潮圩区除涝标准涉及的暴雨历时取值、涝水排除程度确定、起调水位与预降可能性、河道分期实施状况、用地性质变化、水面率控制等影响因素进行分析,以供相关决策部门参考。

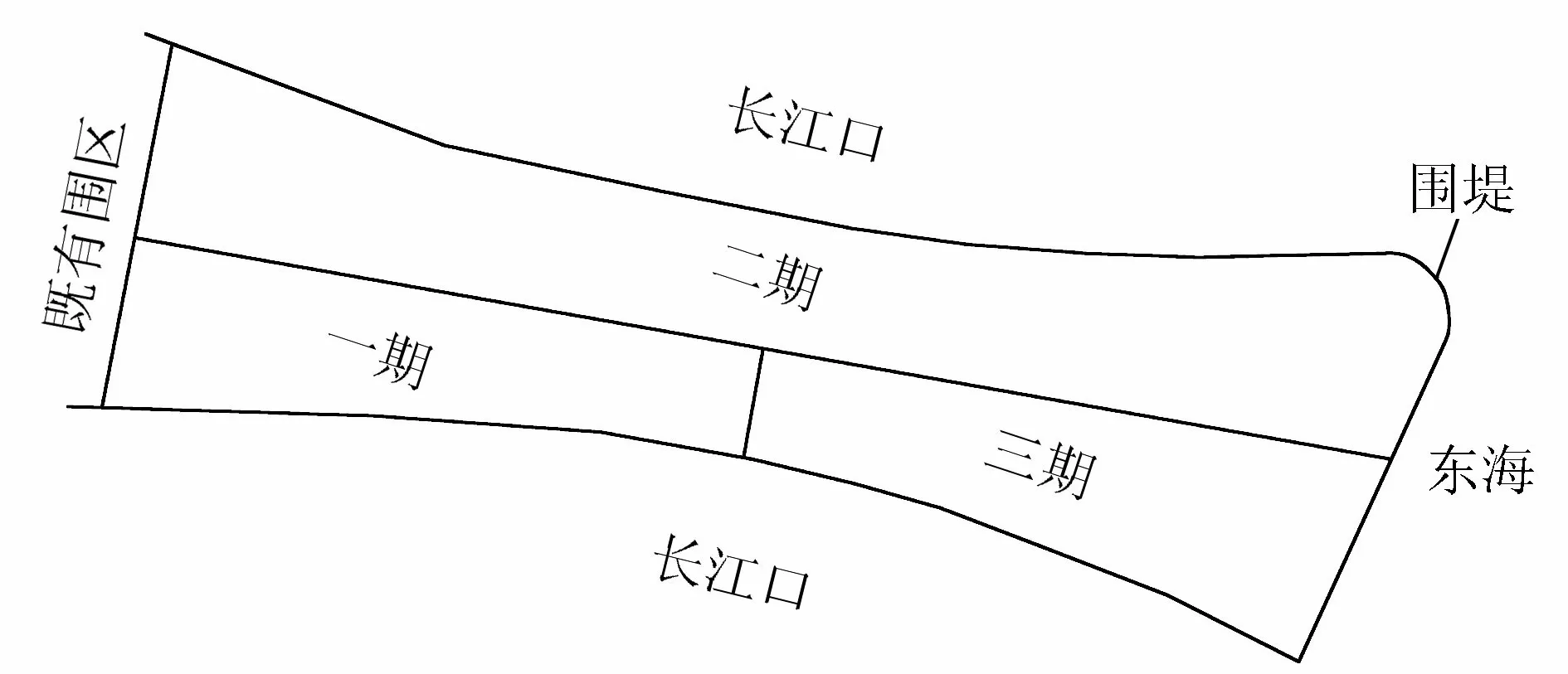
图1 上海某围海造地工程示意图

1 资料及方法

1.1 工程概况

上海某围海造地工程采用促淤、圈围、吹填方式圈围造地约87.9 km2,分3期完成(图1)。一期圈围32 km2已于2015年底完成,二期圈围13.5 km2将于2017年底完成,三期圈围42.4 km2将于2020年底完成。圈围后的土地最终标高为3.00 m,用地性质为现代农业和高端服务业。根据规划,先期根据圈围成陆时机,在围区实施“三横七纵”骨干排涝河道(图2);未来根据开发需要建设蓄淡水湖泊和田间水系工程,最终达到水面率控制要求。排涝河道口宽除纵三河Z3、纵五河Z5和纵七河Z7为50 m外,其余均为80 m,常水位2.20 m时总水面面积约为680万m2。蓄淡水湖泊和田间水系的水面面积不小于320万m2。根据既有周边水系运行情况和场地实施标高,规划常水位为2.20 m,控制最高水位2.70 m;暴雨期提前排水,预降水系河道内水位至1.70 m。

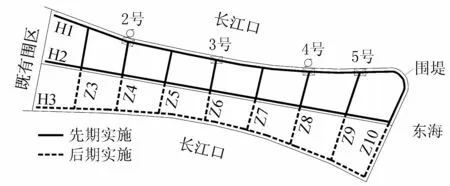
图2 围区水系概化示意图

1.2 分析方法

相关研究显示,新围区域根据不同用地性质可采取不同的除涝排水模式:城市化区域采用市政与水利结合的两级排放模式[12-13],农业开发区域则采用水利区域除涝模式。新围区域为感潮区域,排水受圩外潮位影响较大,受圩外高潮位顶托时采用泵站抽排,圩外潮位低于水系内水位时趁低潮位由水闸自流排出。根据水系特性,考虑采用水量平衡法和一维非恒定流河网水动力数学模型方法分别进行计算和校验。

1.2.1 水量平衡法

视水系河道为水库,采用水库调节方法,将除涝周期划分为若干计算时段,在任何一个时段Δt内,进入水系河道的水量Q入Δt(即降雨量)与流出水系河道的水量Q出Δt之差,等于水系河道内这一时段内蓄水量变化ΔV,即

(1)

(2)

式中:i为降雨强度;A为汇水面积。因排涝期均为暴雨期,蒸发、渗漏等损失量较小,为安全起见可不考虑。Q出根据泵站抽排和水闸自排分别考虑,当水系河道水位低于圩外潮位时,采用泵站抽排量Q出,泵;当水系河道水位高于圩外潮位时,采用水闸自排流量Q出,闸,并按宽顶堰公式计算:

(3)

式中:B为水闸净宽度;h为堰上水头；μ0为综合流量系数,平原地区水闸一般取0.34～0.35[14]。

水系河道蓄水量变化ΔV根据起调水位时的总河道水面积∑S和蓄水水深变化Δh、河道长度L计算,公式为

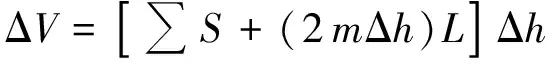
(4)

式中，m为河道边坡坡比。

按上述系列公式,在Excel表中以0.5 h或1 h时间步长建立水系排涝计算过程,进行循环迭代计算,直至收敛。

1.2.2 河网水动力数学模型法

采用一维非恒定流水动力学方法建立河网模型,其基本方程如下:

(5)

(6)

式中:A为河道过水面积,m2;t为时间,s;Q为流量,m3/s;x为沿河距离,m;h为水位,m;R为水力半径,m;C为谢才系数,m0.5/s;g为重力加速度,m/s2;q为单位河长侧向入流量(流入为正,流出为负),m2/s。

对式(5)(6)采用Preissmann四点隐式差分格式进行数值离散,按每个节点的水量平衡解线性方程组。河网水系侧向流入量q为围区降雨河网分区汇水量,就近汇入河道。外海水位边界条件采用潮位过程。谢才系数C由糙率系数计算,糙率系数根据河道特性取0.018～0.025。对于流量Q,当水闸自排时,按宽顶堰公式计算;当泵站抽排时,按泵站设计流量计算。

1.3 计算边界条件

根据规划要求,围区除涝标准按照20年一遇24 h设计面暴雨情况下,河道水位不超过最高2.70 m控制,围区外潮位采用设计暴雨同步潮位过程。

1.3.1 雨型潮型组合

分别采用“63年”雨型潮型组合(图3)和“麦莎”雨型潮型组合(图4)进行计算论证。另外,由于运行期台风、暴雨、高潮“两碰头”或“三碰头”的情况较少,需复核经常性不利雨型潮型组合情况(简称运行期雨型潮型组合)。拟定多年平均高潮位(3.30 m)与多年平均低潮位(0.84 m)组合的潮型,并与“麦莎”台风期的暴雨雨型进行组合,潮型相位与“麦莎”台风期潮型相位相同,如图5所示。

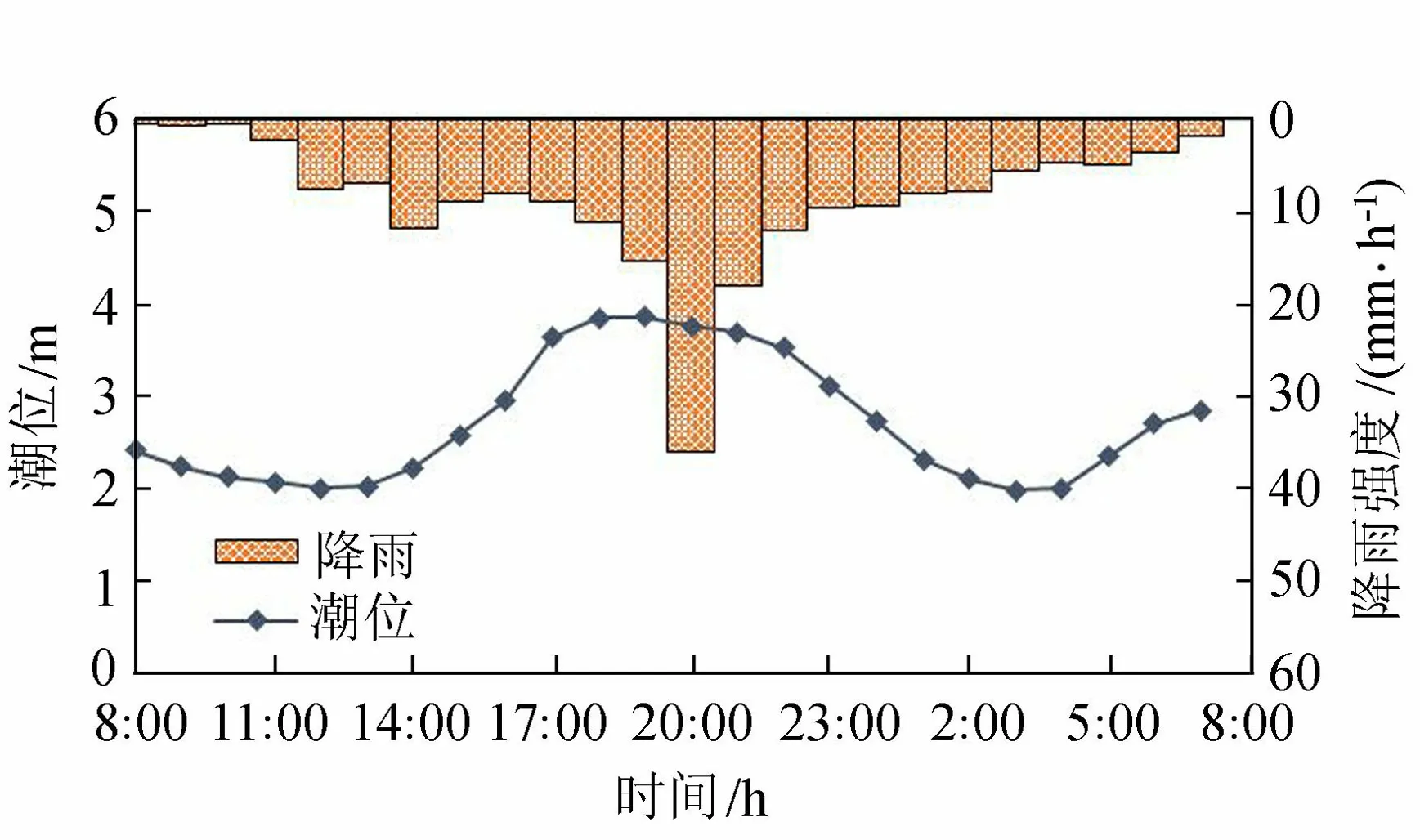
图3 “63年”雨型潮型组合

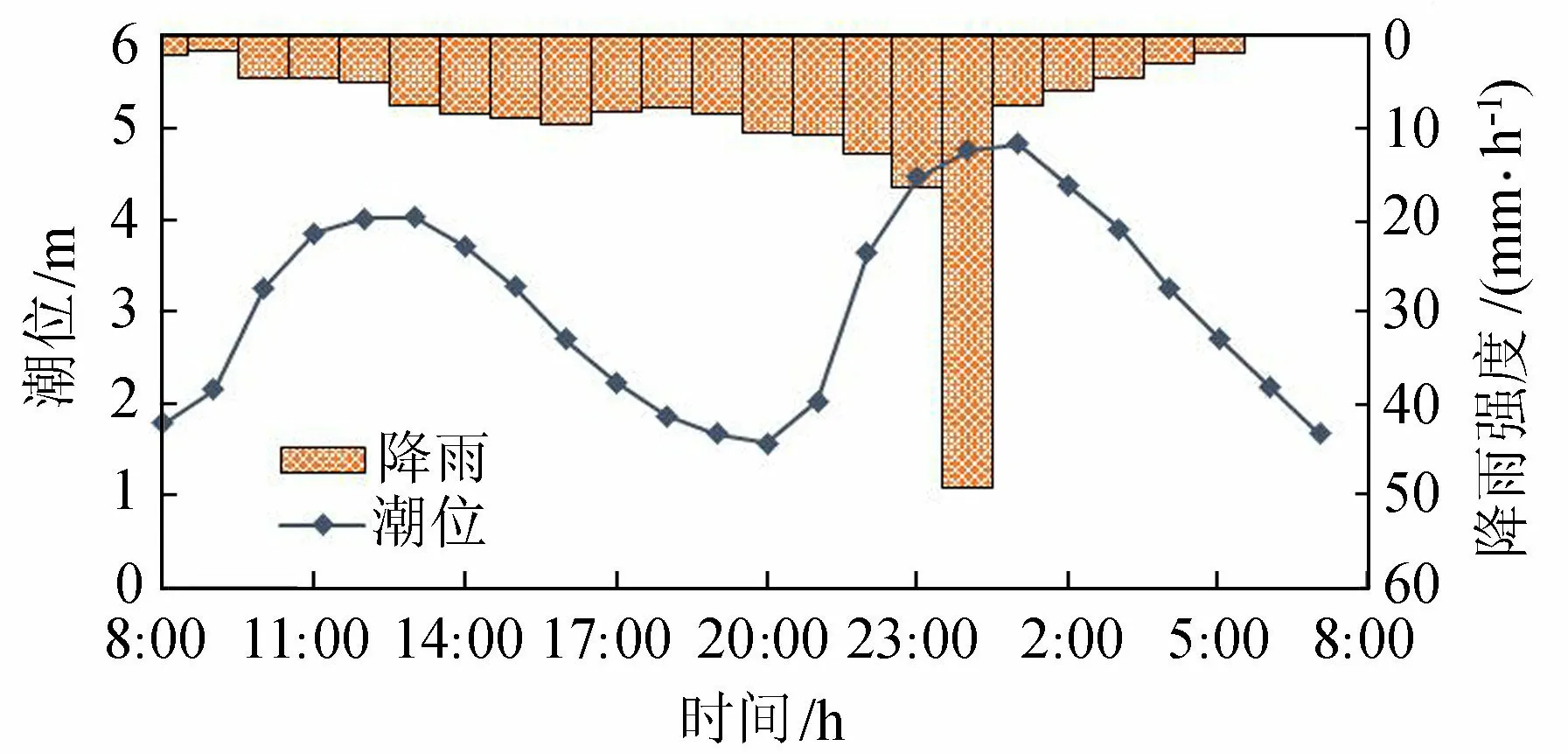
图4 “麦莎”雨型潮型组合

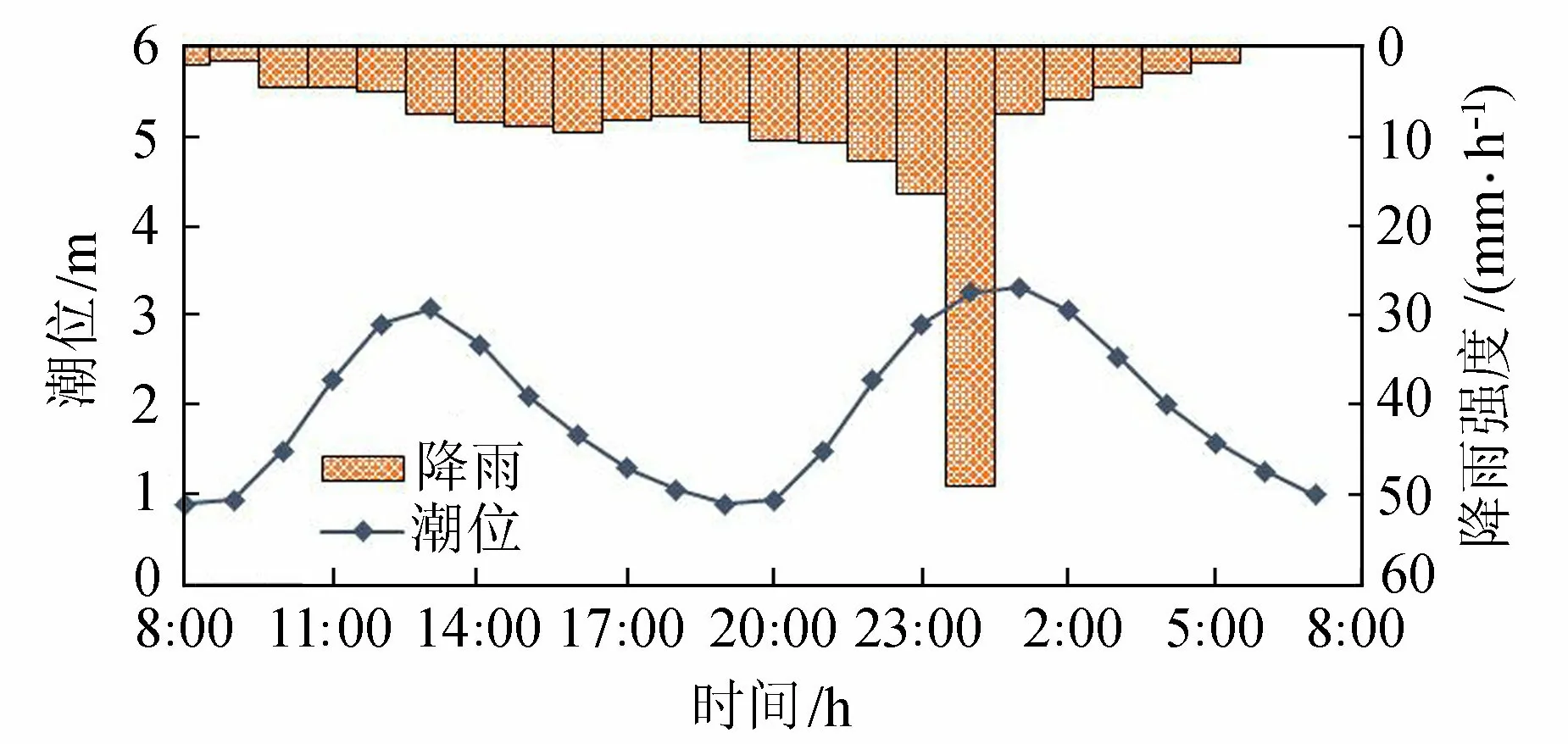
图5 运行期雨型潮型组合

1.3.2 起调水位

规划水系控制水位为1.70～2.70 m,常水位为2.20 m,所以设计除涝规模计算以规划预降的最低水位1.70 m作为起调水位。考虑到降雨前可能未及时预降和避免预降后无充分降雨量,取2.20 m与2.00 m作为校核工况起调水位。

1.4 研究工况

根据围区大小和工程经验,初拟在围区北侧2号和4号位置设排涝泵站与水闸组合枢纽,3号和5号位置单设排涝水闸(图2)。其中,2号和4号泵站的初始计算流量均为40 m3/s,以后以5 m3/s逐级递加;4座水闸初拟净宽均为10 m,以后以2 m逐级递加。计算的目的主要是确定在既定“63年”雨型潮型组合和“麦莎”雨型潮型组合,以及1.70～2.70 m控制水位情况下,合适的泵站排涝流量和水闸宽度。根据上海地区泵站与水闸建设投资情况,以及节能运行要求,运行期应尽量采用水闸排水,所以泵闸规模的确定需综合运行期雨型潮型组合情况下的要求。另外,考虑暴雨前未及时预降水位,需计算起调水位为2.00 m或2.20 m的情况,校核水系最高水位,判定风险。由于建设进度原因,所有骨干水系建成时,田间水系和蓄淡水湖泊并不能同步建成,所以需复核设计雨型潮型组合情况下河道最高水位情况。综合上述要求,拟定计算的工况如表1所示。

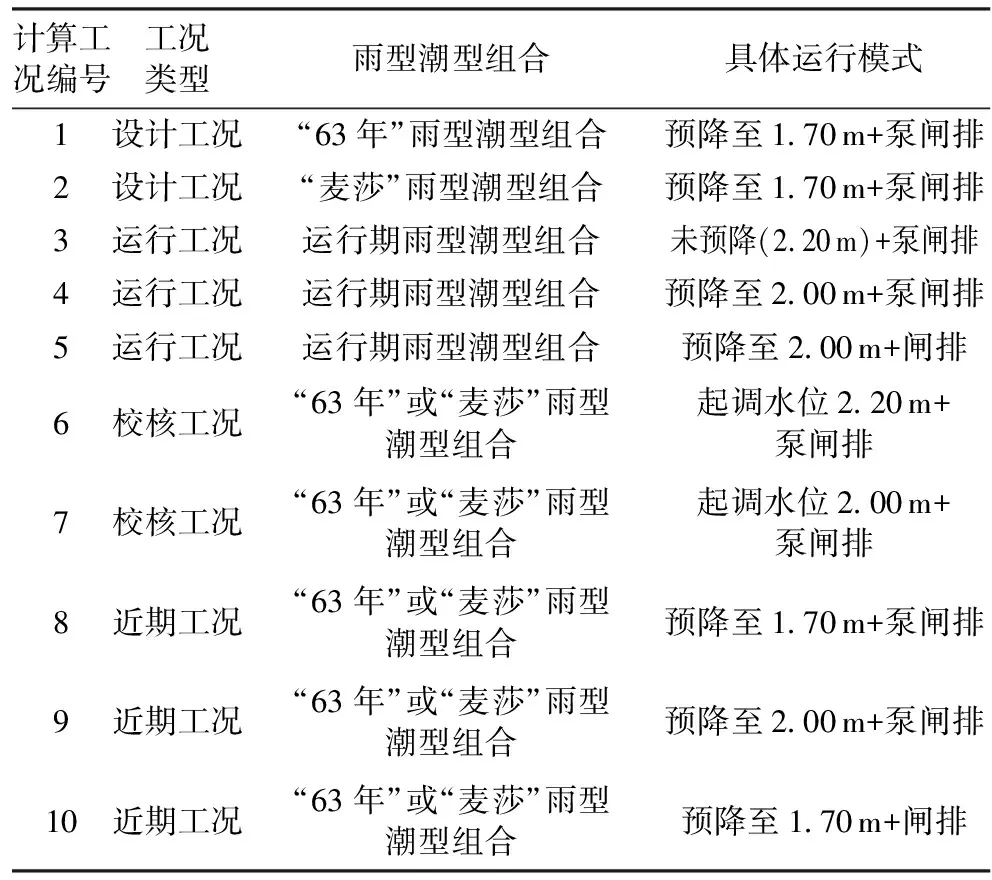
表1 计算工况

2 结果分析

2.1 排水规模初选

经试算,在设计工况下,不论“63年”雨型潮型组合还是“麦莎”雨型潮型组合,2号和4号泵站均采用设计流量40 m3/s不能满足最高水位控制在2.70 m以内的要求,而采用较大设计流量又不经济,比较合适的设计流量为2座泵站均采用60 m3/s与4座均大于12 m的水闸组合。

2.2 计算方法对比

对确定的泵站和水闸规模(2座泵站总流量120 m3/s,4座水闸总宽48 m),采用水量平衡法和河网水动力数学模型法分别计算,结果显示,设计工况下河网水动力数学模型法计算的最高瞬时水位在围区水系的分布基本一致,最高与最低值仅差2 cm(图6)；水量平衡法计算的全围区水系水位为定值。因此，在与本工程面积相近的河网水系内,采用两种方法分析均可满足工程精度要求。为减少计算工作量,以下采用水量平衡法计算成果进行比较分析。

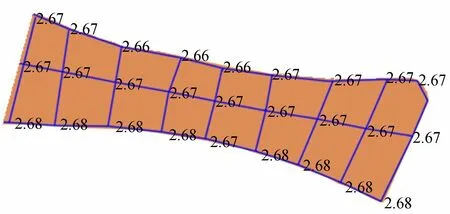
图6 设计工况下河网模型计算的最高瞬时水位分布(单位:m)

2.3 雨型潮型组合影响

为分析“63年”雨型潮型组合与“麦莎”雨型潮型组合对内河水位的影响,以2座泵站总流量120 m3/s和4座水闸总宽48 m为口门建筑排水规模,采用设计工况计算分析。结果显示:虽然在24 h内两种雨型潮型组合情况下的最高水位未超过2.70 m,但24 h末内河水位均高于常水位2.20 m,所以延长计算时间6 h,期间泵站抽排和水闸自排仍按前述原则运行,计算结果如图7所示。结果显示:①“63年”雨型潮型组合情况下,内河最高水位为2.63 m;24 h末泵站排水总量为734.4万m3,水闸排水总量为222.9万m3,期末内河最高水位为2.56 m;30 h末泵站排水总量为864.0万m3,水闸排水总量为273.6万m3,期末内河最高水位2.35 m。期间,2.50 m以上高水位持续时间约12 h,水泵排水约20 h,水闸排水约7 h。若要将内河水位降低至常水位2.20 m,水闸还需开启排水2 h,泵站还需抽排3 h。②“麦莎”雨型潮型组合情况下,内河最高水位为2.68 m;24 h末泵站排水总量为734.4万m3,水闸排水总量为234.4万m3,期末内河最高水位为2.45 m;30 h末排水总量为907.2万m3,水闸排水总量为275.0万m3,期末内河最高水位为2.28 m。期间,2.50 m以上高水位持续时间约8 h,水泵排水约21 h,水闸排水约8 h。若要将内河水位降低至常水位2.20 m,泵站还需运行2 h。

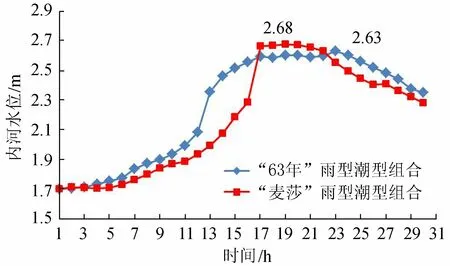
图7 设计工况不同雨型潮型组合内河水位过程线

可见,“麦莎”雨型潮型组合情况下内河最高水位较“63年”雨型潮型组合情况下略高,而在高水位持续时间上“63年”雨型潮型组合情况下要长于“麦莎”雨型潮型组合情况。

另外,为分析雨型潮型组合相位差对水系水位的影响,以“麦莎”雨型潮型组合为原型,将雨型和潮型分别前后移动1 h组合,再次计算水系水位。结果显示:内河水系最高水位分别为2.62 m和2.67 m,均较“麦莎”雨型潮型组合下的水系最高水位要低。

2.4 运行期节能对口门建筑物规模影响

以2座泵站总流量120 m3/s和4座水闸总宽48 m试算,在内河常水位2.20 m状态下突降暴雨,采用泵闸联合排水,内河水位较高,难以满足最高水位控制在2.70 m以内的要求,须调整水闸和泵站规模。

若常水位2.20 m时突降暴雨,采用泵闸联合排水,2座泵站规模保持不变,将4座水闸总宽增加至72 m,内河水位最高达到2.86 m(图8);将4座水闸总宽增加至96 m,内河水位可控制在2.70 m以内;若仅采用水闸排水,且需控制最高水位不超过2.70 m,需将水闸总宽增加至120 m以上。

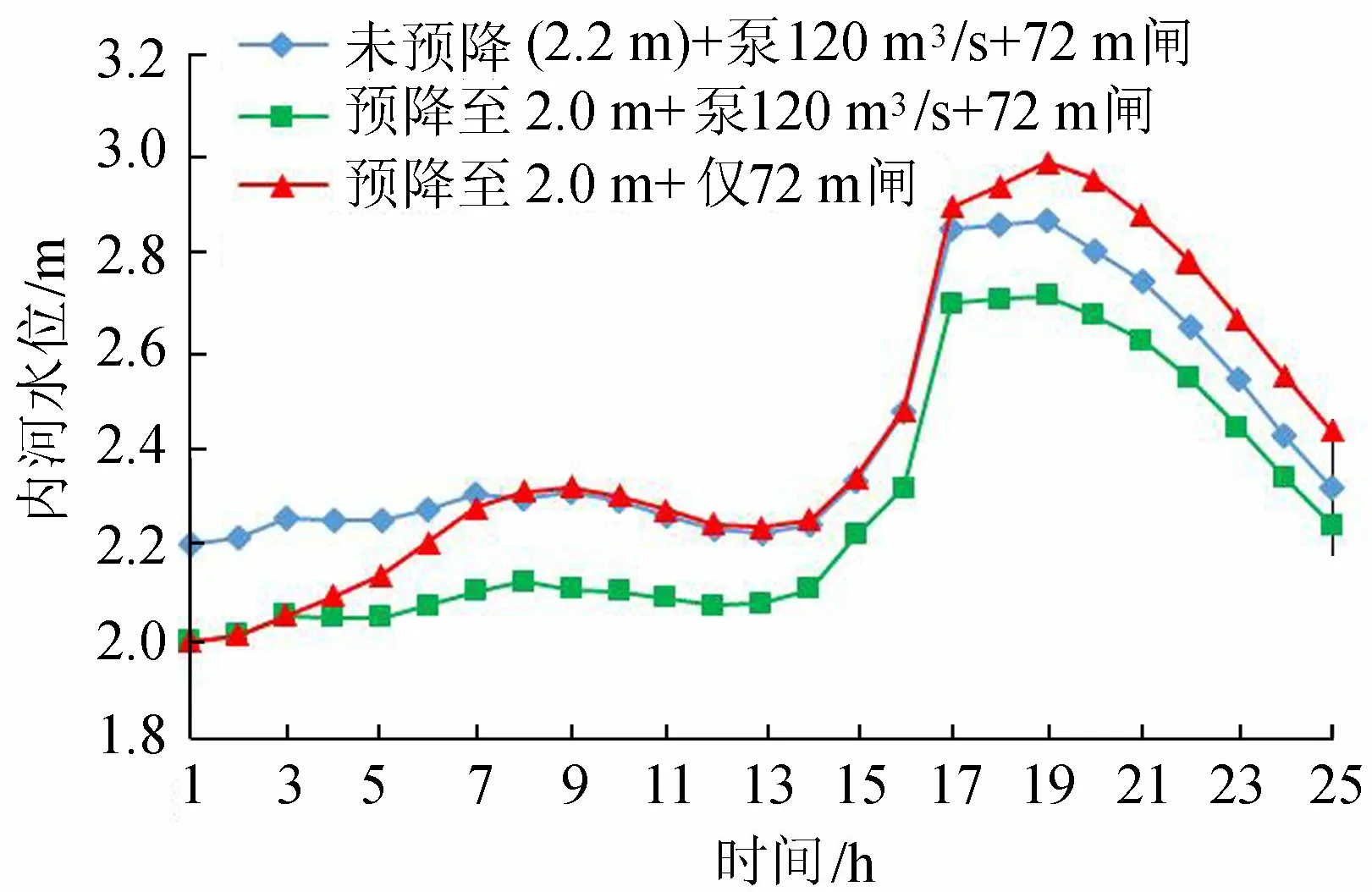
图8 运行期不同排水模式下内河水位过程线

若提前将水位预降至2.00 m,采用泵闸联合排水,2座泵站规模保持不变,将4座水闸总宽增加至72 m,内河水位可控制在2.70 m以内(图8);若仅采用水闸排水,内河水位最高达2.98 m。

2.5 适宜的除涝规模确定

由上述分析,无论“63年”雨型潮型组合,还是“麦莎”雨型潮型组合,受外海潮位顶托,利于水闸自流排水的时间均较短,且水位差不大,水闸自排水量有限,所以要控制水系最高水位主要依靠泵站抽排,泵站的规模应以设计工况下相应设计标准的雨型潮型组合计算结果来确定。但是,运行期经常性情况是低潮位较低,水闸排涝时间较长,且排涝流量较大,为节能要求尽量减少泵站运行提供可能,水闸规模应以经常性的雨型潮型组合确定。

根据计算,泵站的规模以2座泵站总流量120 m3/s较适宜,4座水闸总宽48 m在设计工况下可满足控制设计周期内最高水位要求,但运行期遭遇暴雨情况的不利雨型潮型组合情况下,内河水位较高。在常水位2.20 m情况下,水闸总宽增加至72 m,最高水位还是超过控制要求,但风险可基本接受(超最高控制水位0.16 m,但未超过场地的标高(3.00 m));若暴雨前微降内河水位至2.00 m,则基本可满足最高水位控制要求。因此,推荐采用2座泵站总流量120 m3/s加4座水闸总宽72 m作为水系口门控制建筑物规模。

2.6 “两碰头”前水系水位未预降影响

根据推荐的泵闸规模,计算结果显示,在遭遇暴雨和高潮位的“两碰头”情况下,水系水位若未提前预降,但开始降雨时能及时开始泵站排水,最高水位将达到2.98 m,若暴雨前微降内河水位至2.00 m,则最高水位为2.71 m,基本满足最高水位控制要求。

2.7 近远期实施对水系水位影响

根据计算,在田间水系和蓄淡水湖泊尚未建成时,若提前预降水系水位至1.70 m,水系最高水位将达到3.00 m;若未能提前预降水系水位(常水位2.20 m),水系最高水位将达到3.28 m;若提前预降水系水位至1.70 m,但仅依靠水闸排水,水系最高水位将达到3.51 m;若不提前预降水系水位,且仅由水闸自排,水系最高水位将更高。

3 讨 论

3.1 感潮圩区除涝标准表达方式

对于治涝标准,SL 723—2016《治涝标准》除规定了“应同时以设计暴雨重现期、设计暴雨历时、涝水排除时间和涝水排出程度等指标表示”,还对感潮承泄区提出了“采用2～5年重现期排涝期高潮位或5～10年一遇排涝期平均潮位作为设计水位”“有条件时应选择相应排涝期的典型潮位过程线,并分析涝区涝水与潮水的遭遇条件,考虑天文潮的不利组合因素分析确定”,所以,感潮圩区除涝标准应包括设计暴雨重现期、设计暴雨历时、涝水排除时间、涝水排除程度、设计潮位与过程等指标。

从上述计算分析看,设计暴雨过程(雨型)与设计潮位过程(潮型)组合对感潮圩区除涝规模的确定影响较大,在确定除涝标准时建议加以明确。

3.2 暴雨历时延长和双峰暴雨的风险

对于设计暴雨历时和涝水排除时间,SL 723—2016《治涝标准》规定一般取24 h降雨24 h排除。但由于气候因素,连续降雨导致围区受涝和引起水工建筑物失事的现象也较多。历史上“75·8”石漫滩水库垮坝事件就是由于降雨历时较长,并发生“双峰”暴雨：1975年8月4日11:00开始降雨,5日降雨强度增大,6日降雨减弱,7日降雨强度再次增大,8日1:00降雨减小,5:00雨停,总降雨量1 074.4 m m[15]。另外,有研究表明,上海地区年最大1 d 和3 d 设计暴雨同频遭遇风险率在75%～85%之间,且同现风险率随年最大1 d 设计暴雨值增大而增大[16]。若发生大于24 h降雨历时的“双峰”暴雨,在第一个24 h降雨后,水系水位未排除至设计水位,再次遭遇大暴雨时,就可能发生圩区受涝风险。因此,在确定除涝标准时,若能考虑年最大1 d 和3 d 降水量的遭遇组合,则有利于降低除涝风险。

3.3 涝水排出程度对除涝规模影响

上述结果显示,在设计工况确定的泵闸规模情况下,按照最高水位不超过控制水位的涝水排出标准,24 h末内河水位均高于常水位。若按照24 h末内河水位控制为常水位标准,在水闸规模不变(因设计雨型潮型组合情况下水闸发挥作用较小)情况下,泵站规模需增加至165 m3/s,约增加37.5%;若按照24 h降雨24 h排出,即24 h末内河水位降至预降水位(为降低“双峰”暴雨受涝风险),则在水闸规模不变情况下,泵站规模需增加至260 m3/s,约增加117%。可见,平原感潮圩区的涝水排出程度的确定对除涝规模影响较大。

3.4 预降可能性及其风险

在平原地区,为尽量降低除涝设施规模,水利规划部门经多方案计算分析,拟定了最低预降水位和最高控制水位,以合理增加河道调蓄量和控制河道堤防高度。由于平原地区河网密布,许多河道承担了通航功能,受通航能力影响,河道又有通航最低水位要求,且一般高于水利除涝最低控制水位,因此实际运行时河道低水位又受通航影响,在预报降雨前预降河道至水利规划最低水位较难。另外,由于预报降雨准确性和河道运行管理部门对预降水位的控制准确性,很难在暴雨来临前将河道水位预降至规划最低水位。因此,受多种因素影响,在真正遇到设计工况情况时,河道水位超过规划最高水位的可能性就较大。

3.5 水面率和用地性质变化影响

水面率是控制河道调蓄量的重要指标。适宜的水面率不仅有利于防洪除涝,而且对城市生态环境起着重要作用。SL 413—2008《城市水系规划导则》提出了各区域适宜的水面率控制要求。在新圈围成陆地的区域更应在规划阶段控制水面率,进而减小除涝设施规模,减轻洪涝灾害风险。

随着社会经济发展,土地利用性质会发生变化,尤其是原农业用地、绿化用地转化为建设用地以后,地面硬化,透水性减弱,导致径流系数增加,进而影响降雨产流过程,暴雨产生的峰值径流量增大,尤其是按照短历时暴雨设计的管渠规模将会增大。由于水利除涝采用24 h以上降雨历时,所以对采用水利除涝模式计算的除涝规模影响较小。

4 结 论

a. 在约100 km2区域内,采用水量平衡法和河网水动力数学模型法分析计算水系河道水力要素和除涝设施规模,均可满足工程精度要求。

b. 不同雨型潮型组合情况下内河最高水位和高水位持续时间不同,“麦莎”雨型潮型组合情况下内河最高水位较高,而“63年”雨型潮型组合情况下高水位持续时间较长,后期河道水位也较高。

c. 设计雨型潮型组合情况下,泵站强排对控制内河水系最高水位影响较大,但为减少运行期能耗,应尽量加大水闸规模,利用水闸自流排涝。

d. 暴雨前预降内河水位,增加河道调蓄量,对降低除涝设施规模有利,但需考虑河道水位预降可能性及其风险。

e. 平原感潮圩区除涝标准的确定涉及设计暴雨重现期、设计暴雨历时、涝水排除时间、涝水排除程度、设计潮位与过程等因素,尤其雨型潮型组合对除涝规模影响较大。

[ 1 ] 侯庆志,季荣耀,左利钦,等.曹妃甸海域围填海工程动力地貌环境遥感分析[J].水利水运工程学报,2013(3):1-7.(HOU Qingzhi, JI Rongyao, ZUO Liqi, et al. Remote sensing monitoring and environmental impact analysis of reclamation in Caofeidian sea area [J].Hydro-Science and Engineering,2013(3):1-7.(in Chinese))

[ 2 ] 袁汝华,张长宽,林康,等.江苏滩涂围区功能及产业布局分析[J].河海大学学报(自然科学版),2011,39(2):220-224.(YUAN Ruhua, ZHANG Changkuan, LIN Kang, et al. Function and industry layout of reclamation areas of coastal tidal flats in Jiangsu Province[J].Journal of Hohai University(Natural Sciences),2011,39(2):220-224.(in Chinese))

[ 3 ] 季永兴,卢永金,姚华生.浦东国际机场围海大堤龙口水力数学模型研究[J].水利水电科技进展,2000,20(6):36-38.(JI Yongxing, LU Yongjin, YAO Huasheng. Hydrodynamic model study for beach reclamation closure of Shanghai Pudong International Airport[J].Advances in Science and Technology of Water Resources,2000,20(6):36-38.(in Chinese))

[ 4 ] 王留洋,沈永明.温州浅滩围涂工程对周边水动力环境的影响[J].水动力学研究与进:A辑,2014,29(1):67-75.(WANG Liuyang, SHEN Yongming. Study on hydrodynamic environment of land-making project at Wenzhou shoal[J].Chinese Journal of Hydrodynamics,2014,29 (1):67-75.(in Chinese))

[ 5 ] 王震,邰佳爱,张东生.东壁岛围垦对元洪港区潮流及泥沙淤积影响的数值模拟[J].河海大学学报(自然科学版),2003,31(2):220-223.(WANG Zhen,TAI Jiaai, ZHANG Dongsheng. Numerical simulation of influence of Dongbi Island reclamation project on tidal current and sediment deposition in Yuanhong Port area[J].Journal of Hohai University(Natural Sciences),2003,31(2):220-223.(in Chinese))

[ 6 ] 贾卫红,李琼芳.上海市排水标准与除涝标准衔接研究[J].中国给水排水,2015(15):122-126.(JIA Weihong, LI Qiongfang. Study on linkage between drainage standards and waterlogging control standards in Shanghai [J].China Water & Wastewater,2015(5): 122-126.(in Chinese))[ 7 ] 唐迎洲.不同暴雨等级下崇明岛除涝能力评估[J].水资源保护,2011,27(3):42-44.(TANG Yingzhou. Evaluation of waterlogging drainage capacity in different rainstorm conditions on Chongming Island[J].Water Resources Protection,2011,27(3):42-44.(in Chinese))

[ 8 ] SHAHAPURE S S,ELDHO T I,RAO E P. Flood simulation in an urban catchment of Navi Mumbai City with detention pond and tidal effects using FEM, GIS, and remote sensing[J].Journal of Waterway, Port, Coast and Ocean Engineering,2011,137(6):286-299.

[ 9 ] KULKARNI A T,ELDHO T I,RAO,E P, et al. An integrated flood inundation model for coastal urban watershed of Navi Mumbai, India [J].Nature Hazards,2014,73 (2):403-425.

[10] 胡泽浦.2005年“麦莎”和“卡努”台风影响上海的特点分析及对策建议[J].城市道桥与防洪,2007(4):9-14.(HU Zepu. Characteristic analysis of influence of typhoons “Maisha” and “Kanu” on Shanghai in 2005 and counter-measure suggestion [J].Urban Roads Bridges & Flood Control,2007(4):9-14.(in Chinese))

[11] 虞美秀,杭庆生,贾卫红,等.上海市设计潮位及典型过程推求[J].人民长江,2015,46(增刊1):77-79.(YU Meixiu, HANG Qingsheng, JIA Weihong, et al. Design tidal level of Shanghai City and derivation of typical tidal curve[J]. Yangtze River, 2015, 46(Sup1): 77-79.(in Chinese))

[12] 刘水芹,季永兴.平原城市化区域雨水二级排放规模的确定[J].灌溉排水,2000,19(4):45-48.(LIU Shuiqin, JI Yongxing. Study on two stage drainage scale of rainwater in urbanized region[J].Irrigation and Drainage,2000,19(4):45-48.(in Chinese))

[13] 谢华,黄介生.平原河网地区城市两级排涝标准匹配关系[J].武汉大学学报(工学版),2007,40(5):39-42.(XIE Hua, HUANG Jiesheng. Research on matching relations of two-stage drainage systems for city in plain river network area[J].Engineering Journal of Wuhan University,2007,40(5):39-42.(in Chinese))

[14] 吕列民.平原水闸泄流能力计算与试验[J].南昌大学学报(工科版),2005,27(3):30-33.(LÜ Liemin. Discharge calculation and experimental for plain sluice [J]. Journal of Nanchang University(Engineering & Technology),2005,27(3):30-33.(in Chinese))

[15] 吴旭. 石漫滩水库的“75·8”事件[J].中国防汛抗旱,2005(3):27-37.(WU Xu. “75.8” flood incident of Shimantan Reservoir, China [J]. China Flood and Drought Management, 2005(3):27-37.(in Chinese))

[16] 曾明,张雨凤,李琼芳,等.上海市不同历时暴雨组合概率研究[J].水资源保护,2015,31(4):82-86.(ZENG Ming, ZHANG Yufeng, LI Qiongfang, et al. Study on probability for rainstorm combinations during different durations in Shanghai City[J].Water Resources Protection,2015,31(4):82-86.(in Chinese))

Studyonrainfall-tide-combinationsimpactingonthedrainagescalesinaplaintidalarea

JI Yongxing1, 2, LIU Shuiqin3

(1.ShanghaiWaterEngineeringDesignandResearchInstitute,Co.,Ltd.,Shanghai200061,China; 2.EngineeringResearchCenteronFloodControlandDisasterAlleviation,ShanghaiWaterAuthority,Shanghai200061,China; 3.ShanghaiHydrologyAdministration,Shanghai200332,China)

Based on the water budget method and a river-network numerical model, the drainage effects of the rainfall-tide-combinations were analyzed through the scenario of a certain tidal polder in Shanghai. Factors involving the drainage criteria, such as the value of rainstorm duration, the determination of drainage degree, the possibility of starting regulation level and pre-reducing water level, the short and long-term implementation of river regulation, the land usage transition and the controlling of the water surface ratio, were analyzed. The results indicate that in the study area of 100 km2, the river hydraulic factors and the scales of the drainage facilities calculated by both the water budge method and the numerical model fulfill the engineering accuracy. For a certain drainage scale, the peak water levels and their durations vary under the different rainfall-tide-combinations. The peak water level is relatively large under the “Matsa” case,yet the duration of the high-water-level stage is longer and the water level is higher in the later stage under the “63-year” case. The technical standards of drainage in a plain tidal polder are related to the design rainstorm recurrence interval, the design rainstorm duration, the drainage time, the degree of the drainage, the design tidal level and tidal process. In addition, the rainfall-tide-combinations can highly affect the scale of drainage ability.

plain tidal area; polder; rainfall-tide-combinations; drainage criteria; drainage scale

上海市科委2013年度创新行动计划(13DZ2251500)

季永兴(1970—),男,教授级高级工程师,博士,主要从事水利工程设计工作。E-mail:jiyx@sh163.net

10.3880/j.issn.1006-7647.2017.05.004

TV212.5+3

：A

：1006-7647(2017)05-0022-06

2016-12-19 编辑：熊水斌)