不同底缘形式的平板闸门水力特性数值模拟
2017-09-16赵梦丽冷东升邢仕强
刘 昉,赵梦丽,冷东升,邢仕强
(天津大学水利工程仿真与安全国家重点实验室,天津 300072)
不同底缘形式的平板闸门水力特性数值模拟
刘 昉,赵梦丽,冷东升,邢仕强
(天津大学水利工程仿真与安全国家重点实验室,天津 300072)
为优化闸门体型,探究不同底缘形式下闸门的水力学特性,采用RNGk-ε模型和VOF方法,结合动网格划分技术,对高水头平板闸门闭门过程中水力学特性进行了数值模拟分析。采用模型试验实测数据验证了数值方法的可靠性;利用非平稳随机过程处理技术(EMD),有效地提取底缘压力趋势项,进而开展底缘形式与水流脉动、持住力相关关系的探讨;通过综合考量底缘压力脉动、空化及持住力特性,寻求最佳底缘体型。结果表明, 闸门底缘形式的改变对启闭力影响显著,前倾角底缘形式启闭力最小,底缘压力脉动较小,最不易出现空蚀破坏。
平板闸门;动水闭门;数值模拟;水动力特性;底缘形式;经验模态分解
平板事故闸门因其动水关闭过程中的水动力特性非常复杂,一直是闸门设计及研究的重点和难点,尤其是闸门启闭力特性[1-3]和闸区空化特性成为学者们关注的焦点。高速水流下的闭门过程流态不同于闸门全开或局开工况,为强烈的水气两相紊流流动,闸后水流由满流过渡到明流,若底缘体形设计不合理,将会造成闸下水流流态不佳,门体形成负压,底缘因水流分离而导致的压力波动亦会诱发闸门振动,给闸门体系带来安全隐患。
闸门底缘倾角的朝向、角度均是影响启闭力的关键因素。早期研究人员主要采用模型试验方法探究闸门底缘形式与启闭力的相关关系,通过直接改换闸底体型,测试连接在闸门及启闭机之间钢丝绳的受力,反推闸门的启闭力,方法简单易于操作,却存在缩尺效应,且实测物理量有限,无法直接反映作用在闸门底缘处的上托力或下吸力的大小,不利于闸门受力机理的研究。随着数值方法的成熟及软件的完善,李利荣等[4]曾利用数值计算方法,模拟分析水力自动滚筒闸门表面的动水压力、流速分布等水动力特性;张冬等[5]通过ADINA软件对平面闸门不同开度下启闭力的变化特征进行研究;章晋雄等[6]采用RNGk-ε模型和水-气两相VOF模型,分析比较不同上游底缘倾角对上托力的影响。前人的闸底体型数值工作大多集中于倾角角度的研究,且综合考量底缘倾角、朝向对闭门力及底缘脉动和空化特性影响的相关报道鲜少。鉴于此,本文以某泄洪洞内事故平板闸门为研究对象,采用RNGk-ε模型和VOF方法对闸门静态持住力进行试验验证,并在考虑底缘脉动和空化特性基础上,开展底缘倾角、朝向与闸门闭门力相关关系的探讨,寻求最优的底缘形式,以期为高水头事故闸门设计提供借鉴。
1 模型建立
1.1 模型方程和数值方法
N-S方程采用有限体积法进行离散,压力速度的耦合求解选用PISO算法[7]。紊流模型选取考虑各向异性效应的RNGk-ε模型,该方法在处理流线弯曲及瞬态问题方面较标准k-ε模型更具优越性。
闸井内水气两相交界面的追踪可利用VOF法[8]实现,VOF法通过建立和求解计算网格内流体体积函数αw的输运扩散方程来捕捉自由表面。当第w相流体体积函数αw=1则单元体内充满流体,反之αw=0则单元内无该相流体,αw=0~1之间表明单元体积内半充满流体,即此单元为自由表面单元。
第w相流体体积函数输运扩散方程:
(1)
式中:αw为第w相流体体积函数;xi为i方向流体位移;ui为i方向流体速度。
水气两相流中,单元体内密度ρ和速度u可表示为
(2)
(3)
式中:ρw为水的密度;ρa为气的密度;uw为水的速度;ua为气的速度。
VOF法简便易行且无须占用大量内存和CPU。在模型建立时,为预防库区水流波动溢出,所建库高超出水面1/3。
1.2 边界条件和初始条件
本文依托于某水利工程,其右岸设有长759.7 m的泄洪放空洞,采用有压洞接无压洞布置型式。在距进水口约94 m的下游设置1扇平板事故闸门,孔口宽6.0 m、高12.0 m,设计水头100 m。闸门下游84 m处布置1扇弧形工作闸门,孔口宽7.0 m、高6.5 m;事故闸门上游面板止水,底缘采用下游倾角30°的布置型式,并在门槽下游预留缺口进行补气。
计算模型总长259 m,上游水库长度为5倍的进口高度,下游模拟至弧形闸门出口。水库进口通过自编程序UDF,设置为静压分布压力入口边界;库顶及闸井顶部定义为空气入口边界条件,弧门出口给定1个大气压力出口边界条件,并以平板闸门全开时恒定泄流流场作为闭门瞬态问题的初始条件。边界条件设置如图1所示。
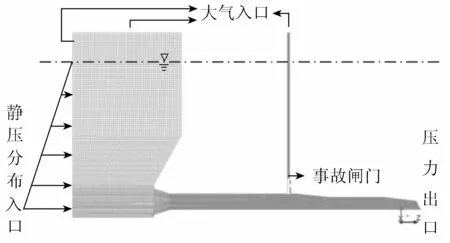
图1 计算模型边界条件设置
1.3 网格划分
网格划分优劣直接关系计算的收敛性、准确性,为提高网格质量,整个计算区域以六面体网格为主,复杂渐变区采用四面体网格形式,并对计算关注区——事故门槽附近进行局部网格加密,总网格数共计124万个。
考虑到闸门闭门为单向运动,可结合“域动网格”更新技术和动态分层方法[9]进行动网格划分。动态分层法即在闸门运动边界相邻处根据运动规律动态增加或减少网格层数,适用于结构化网格,通过设置适当的分层和缩减系数,更新后的网格依然为均匀结构化网格,因此对计算精度影响较小。“域动网格”则是设置一个包含闸门运动边界的内部计算域,该计算域与外部静态计算域分界面定义为变形边界,闸门上下界面给定刚体运动边界,这样即可通过内部计算域的整体运动模拟域内闸门的运动(图2)。上述两种方法的结合有效避免闸门区网格更新后的畸变,从而保证网格质量,提高计算精度。
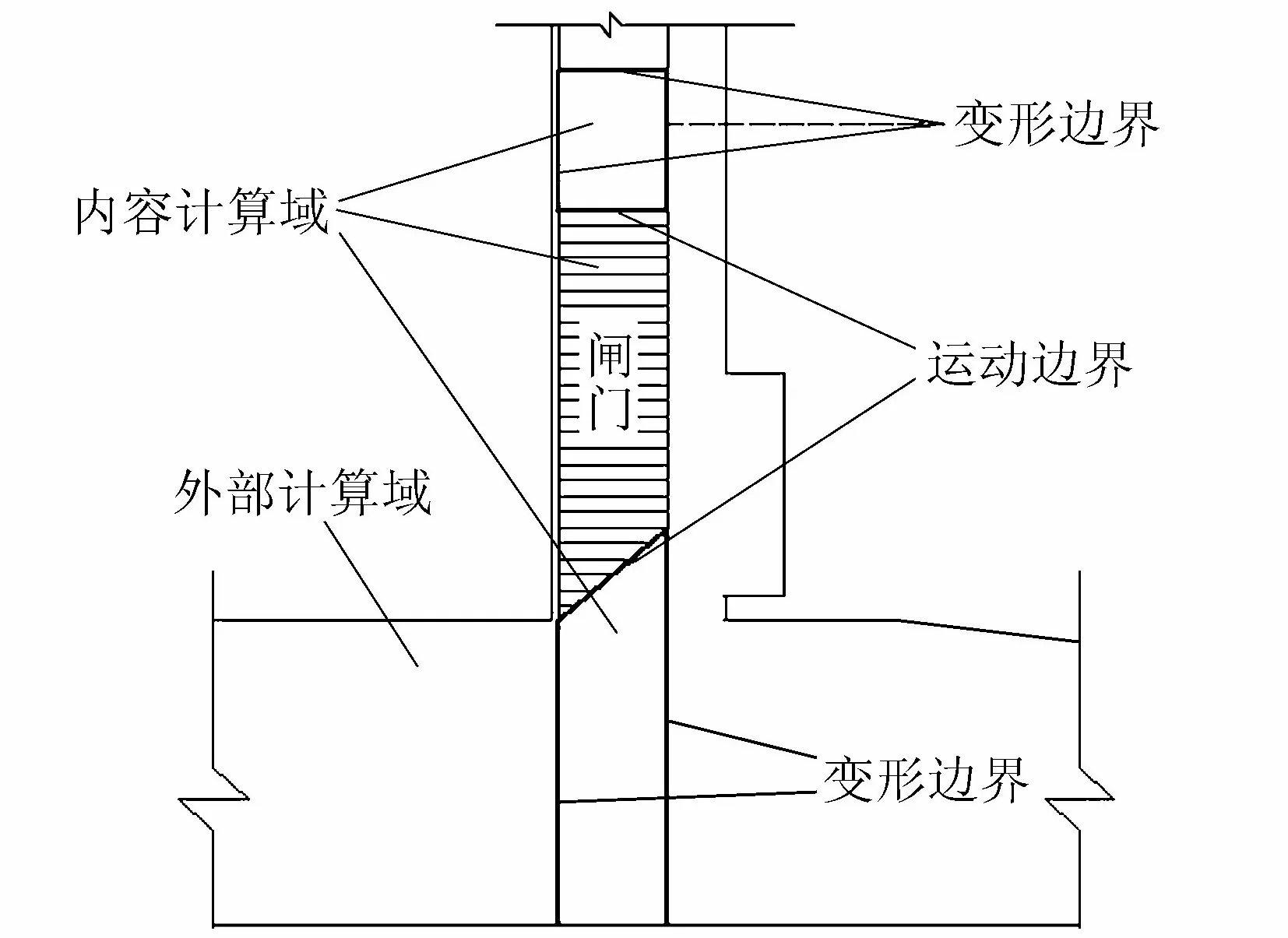
图2 “域动网格”界面设置示意图
2 模型验证
潜孔式平面钢闸门持住力FT的计算根据SL 74—2013《水利水电工程钢闸门设计规范》确定:
(4)
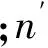
选取上游水头100 m、工作门相对开度0.92(工况1)及上游水头85 m、工作门相对开度0.46(工况2)两种工况为计算工况,通过数值计算求得不同事故闸门相对开度状态下的静态持住力(图3),并与实测结果进行验证。因数值方法模拟摩擦力困难,且不同底缘形式摩阻特性一致,摩擦力对底缘选型无影响,故未做考虑。因此持住力的计算值整体高于试验值,且差值随事故门相对开度的增加而增大。由表1可知,工况1和工况2的事故闸门静态持住力最大计算误差分别为5.8%和7.0%,对应事故相对开度分别为0.62和0.33,其他开度均低于6.0%,满足计算精度要求,验证了计算模型的可靠性。
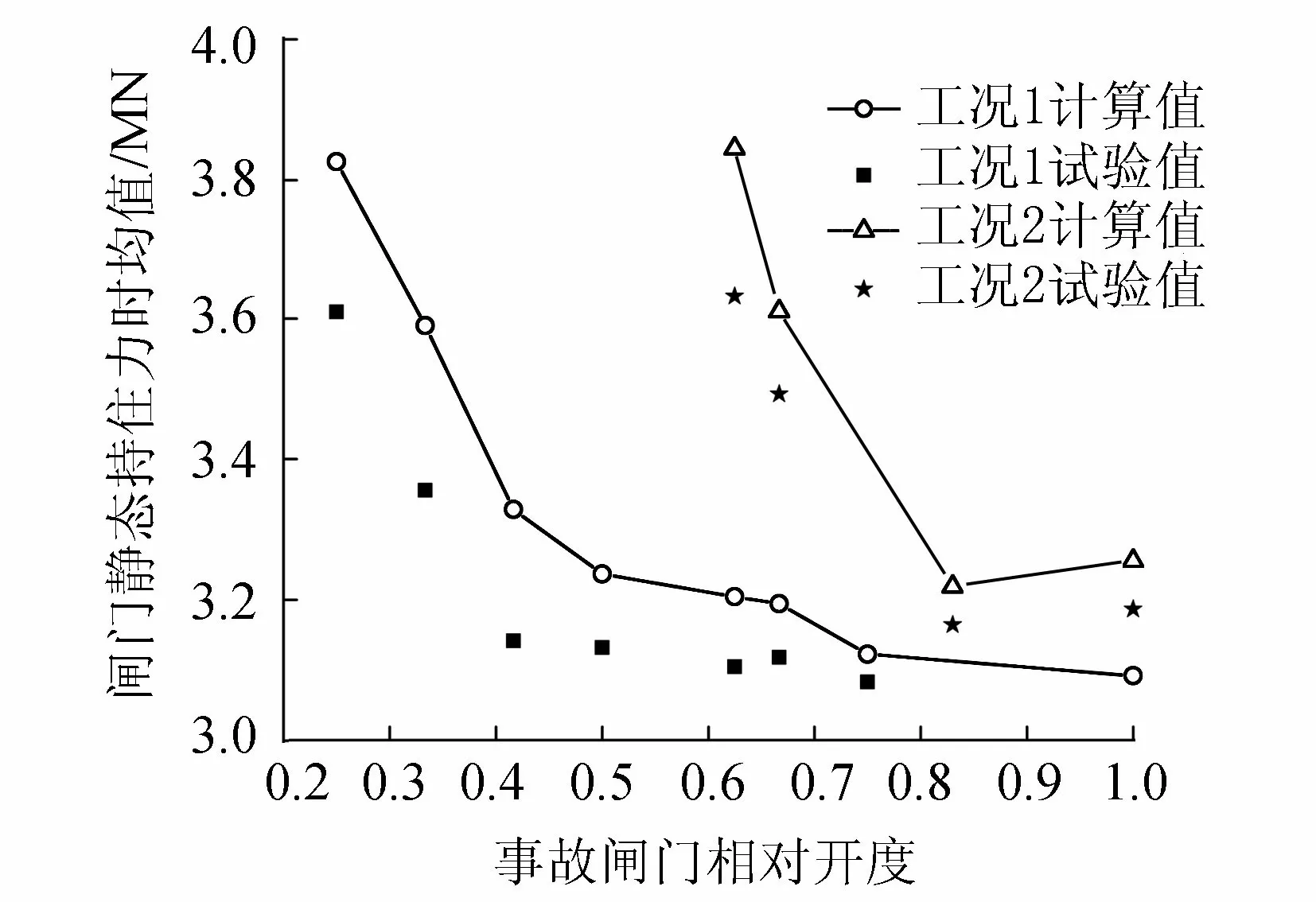
图3 闸门静态持住力验证
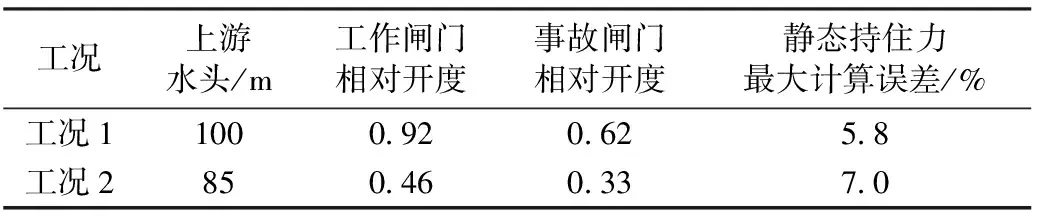
表1 2种工况下静态持住力最大计算误差
3 不同底缘形式的水力特性
对于高水头事故闸门,形成闸门持住力的主要因素为水流的下曳力(或上托力)。底缘形式的变化将改变闸下水流形态,影响底缘压力分布情况,进而转变闸底的受力。本文对平底底缘、后倾角30°(原体型)、后倾角45°、前倾角45°及前倾角45°后倾角30°(图4)这5个体型进行对比研究,分析工况1下闸门底缘压力脉动特性、时域变化情况,研究其空化特性,并对底缘选型进行初步探讨。
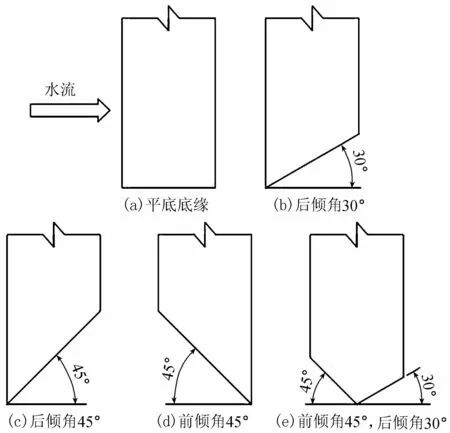
图4 平板闸门底缘选型
3.1 底缘压力脉动特性
事故闸门在连续闭门过程中,闸门底缘的平均压强随其位置的改变而变化,底缘脉动压强亦随闸后流态的转变而变化,故计算得到的压力时程曲线为一非平稳随机过程。为探究不同底缘形式下闸底的稳定特性,获得底缘脉动压力的统计特征,首先要解决的是非平稳随机过程的趋势项剔除问题。目前,趋势项剔除的方法大致可分为如下几类:拟合法[10]、模型法、滤波法、小波法等。其中,经验模态分解(empirical mode decomposition,EMD)能够有效的提取简单及复杂的趋势项成分,获得平滑的趋势项信号[11]。鉴于此,本文利用EMD[12]方法,滤除计算压强曲线的趋势项部分,得到脉动压强时程线,并结合数据分段处理技术,获得时变均方根计算曲线。
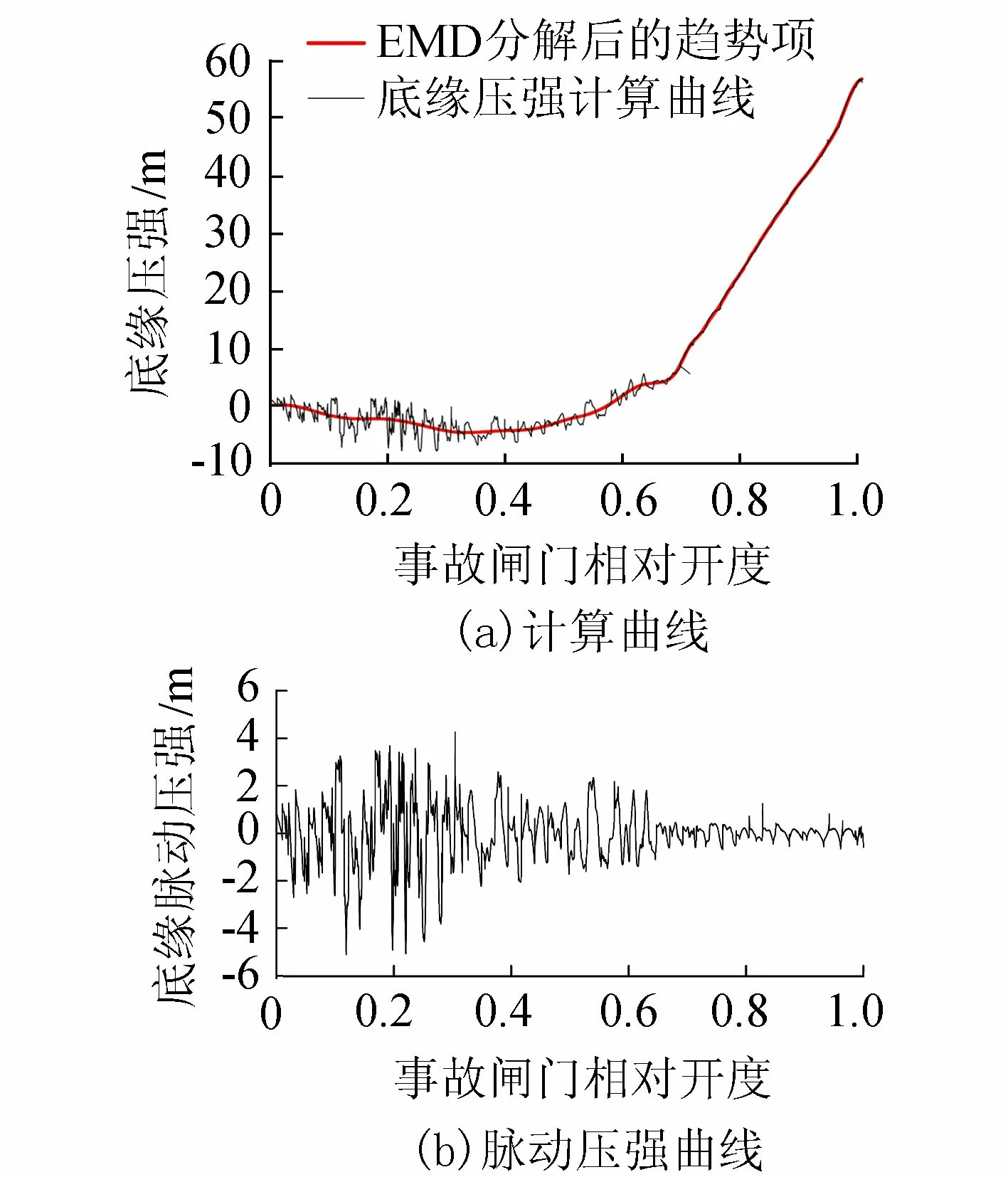
图5 底缘压强脉动特性(后倾角30°)
以后倾角30°为例,给出该体型下闸底压强计算曲线、EMD分解后的趋势项线及脉动压强曲线如图5所示(本文压强均以压力水头计,单位为m)。结果表明:EMD对于数值计算结果同样适用,通过重构获得的趋向性信号能够有效反映底缘压力的整体变化趋势;此外,闸底脉动压强基本在0 kPa附近上下波动,闸后为明流流态时,波动幅度显著增大;上述脉动压强时程线虽能反映闸底压力脉动情况,却无法直观、定量地给出各体型的稳定特性。通过引入时变均方根参数对比发现:平底底缘脉动压强最大时变均方根为2.6 m,数值最大,紧跟随后的为前后倾角组合形式,后倾角30°和前倾角45°最大时变均方根相当,后倾角45°最大时变均方根最小,为1.94 m。
3.2 闭门力
图6为闭门过程中各底缘形式的压力趋势线,可以看出:闸门底缘形式对启闭力的影响显著。底缘倾角朝向上游,其压力在整个闭门过程中表现为上托力,随着闸门开度的增加,底缘压力先小范围内陡然上升,后持续下降至最低点,最后迅速增至100 m水柱附近。对于后倾角和平底底缘而言,底缘受力形式与闸后流态有关,门后满流流态易形成上托力,明满流或明流流态形成下吸力。压力曲线变化趋势类似于上游倾角形式,闸门全开时底缘压力最大,约56 m水柱。闸后为明流流态后,闸门底缘出现水流分离现象,闸下产生负压,由于水流旋滚掺气越来越剧烈,闸门的下吸力达到最大,随着事故门开度的继续减小,闸后通气逐渐充分,闸底负压减小,下吸力降至为0 kN。对比两种后倾底缘形式,闸门后倾角由30°增至45°,底缘最大负压从7.67 m水柱降至7.28 m水柱,减小5.0%,下吸力随下游倾角增大而减小,这与文献[14]中的结论相符。明流流态时平底形式的底缘压力整体低于后倾30°的底缘压力,最大负压相差1.11 m水柱,且其负压持续开度较长。前后倾角组合形式,底缘压力基本呈上托力,计算曲线整体位于前、后倾角底缘之间。
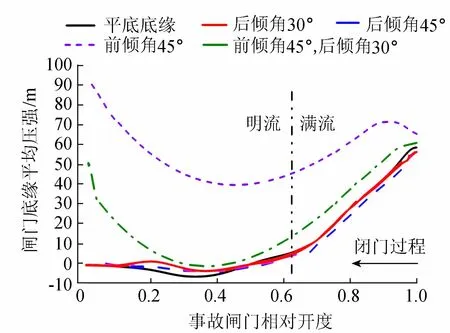
图6 闸门底缘压强趋势线
3.3 闸底空化特性
3.3.1 闸底空化特性
底缘空化特性是判断闸底体型好坏的关键指标之一。为此,通过分析各体型下水流空化数随闸门开度的变化情况,探究闸下压力分布特性,寻求最优底缘体型。
按照SL 74—2013《水利水电工程钢闸门设计规范》,水流空化数K的计算公式如下:
(5)
式中:v1为闸门底缘的平均流速,m/s;H1为底缘相对压强,m;Ha为大气压强,m;Hv为汽化压强,取0.25 m。
水流空化数K随闸门开度的整体变动趋势与底缘压强变动趋势基本一致。上游倾角和前后倾角组合形式:随闸门开度的减小,K值先降后升,在0.4开度附近出现最小值,分别为1.22和0.20。下游倾角和平底底缘K值随开度的增大而减小,闸后为明流时水流空化数均小于0.6,其中平底底缘K值最小,为0.06,计算结果见表2。
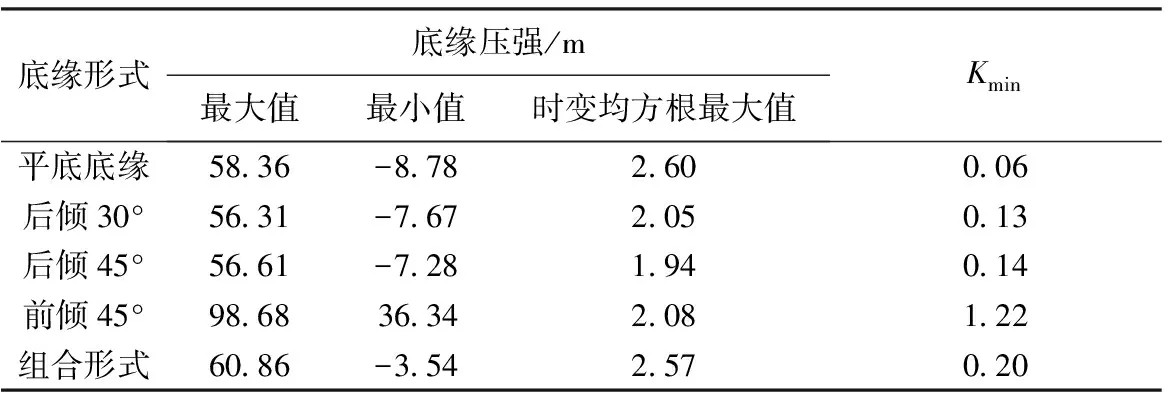
表2 各底缘形式计算结果
3.3.2 闸底压力分布特征
取事故闸门相对开度为0.25时的闸下压力分布情况进行研究,计算结果见图7。平底底缘和组合倾角形式的后半面底缘出现较显著的低压区,水流分离点在靠近负压区的上游侧,当水流脱壁时,闸下射流与底缘之间形成空隙,若空隙得不到及时补气,闸底产生负压。后倾角底缘,若倾角设计得当,底缘处无明显负压,过闸流态良好,补气充分。前倾角底缘整体压力较大,发生空蚀破坏的可能性最低。
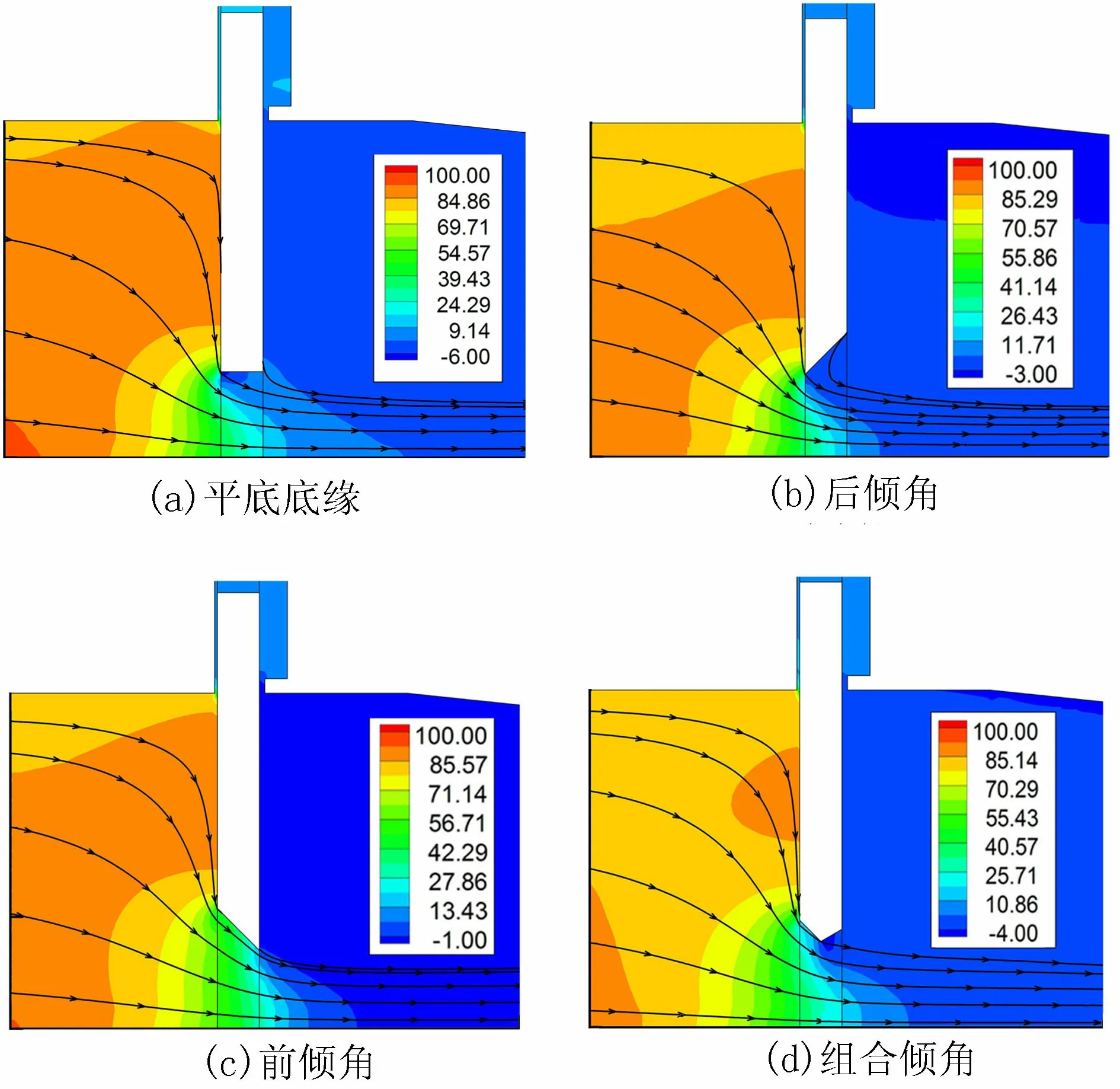
图7 闸门区压强分布云图(单位:m)
3.4 底缘选型初步探讨
综合分析:①前倾角底缘形式,闸下易形成上托力,进而降低闸门的启闭力,故对靠自重无法下门的事故闸门不利;若上游倾角布置合理,闸门底缘几乎无水流分离点,过闸水流流态稳定,闸底脉动情况适中,底缘空化数较大,发生空蚀破坏的可能性最低,且压力分布情况最优。②后倾角底缘形式,闸后明流流态时底缘压力呈下吸力,有利于闸门的落门;该体型闸底上游侧易产生空蚀破坏,底缘倾角的增大可改善闸下流态、提高闸门稳定性、增大水流空化数、降低闸门的闭门持住力。③前、后倾角组合形式的底缘,闸下流态较后倾角底缘复杂,水流脉动较高,计算空化数整体虽高,但后半面底缘压强过低,最易发生空蚀破坏,可尝试增大底缘后倾角以改善闸底流态;此外,该体型部分利用水柱下门,整体底缘压力位于前倾角和后倾角之间。④平底底缘形式,闸下水流条件较差,水流脉动最强,空化数最低,所需启闭力最大,适用于小型工程中的闸门。
在考虑闸底压力分布特性的基础上,从降低启闭力、提高闸门稳定性、减小底缘空化数三者综合考量,各底缘形式优先级由低到高依次为:平底底缘、组合底缘体型、后倾30°、后倾45°、前倾45°。
上述优选体型适用于能靠自重下门的闸门,对于无法靠自重下门的闸门还需另行设计考量。
4 结 论
a. 数值模拟得到的规律和试验结果基本吻合,说明本文所采用的数值方法较合理。
b. 通过EMD方法提取底缘压力计算曲线的趋势项,获得闸底水流脉动特征,结果表明后倾角45°脉动最小。
c. 闸门底缘形式的改变对启闭力影响显著。前倾角或前、后倾角组合形式,闸底压力基本呈上托力,降低闸门的启闭力;平底底缘和后倾角底缘的闸底受力形式与闸后流态有关,满流流态表现为上托力,明满流或明流流态呈下吸力,且下游倾角的增加会降低下吸力,进而减小闸门的启闭力。
d. 底缘空化特性因底缘形式而异。按发生空蚀破坏的可能性由低到高依次排序:前倾角45°、后倾角45°、后倾角30°、前后倾角组合形式(主要是后半底面)、平底底缘。
e. 综合考量,对能靠自重下门的事故门而言,前倾角45°方案最优。
[ 1 ] 肖兴斌,王业红.高水头平板闸门水力特性研究[J].水利水电科技进展,2001,21(4):29-32.(XIAO Xingbin,WANG Yehong.Study on hydraulic characteristics of high head plain gate[J].Advances in Science and Technology of Water Resources,2001,21(4):29-32.(in Chinese))
[ 2 ] NAUDASCHER E,KOBUS H E’,RAO R P R.Hydrodynamic analysis for high-head leaf gates[J].Journal of the Hydraulics Division,1964,90(3):155-192.
[ 3 ] 李丹,田士豪,段亚辉,等.天生桥二级水电站事故检修闸门动水下门试验[J].武汉大学学报(工学版),2009(3):284-286.(LI Dan,TIAN Tuhao,DUAN Yahui,et al.Experiment on shutting of emergency overhaul gate in surge shaft of Tianshengqiao Cascade II Hydropower Station[J].Engineering Journal of Wuhan University,2009(3):284-286.(in Chinese))
[ 4 ] 李利荣,王福军,文恒,等.水力自动滚筒闸门水动力特性数值模拟[J].水利学报,2010,41(1):30-36.(LI Lirong,WANG Fujun,WEN Heng,et al.Numerical analysis of hydrodynamics for hydro-automatic roller gate[J].Journal of Hydraulic Engineering,2010,41(1): 30-36.(in Chinese))
[ 5 ] 张冬,张燎军,陈超,等.高水头平面钢闸门启闭力数值模拟研究[J].水电能源科学,2014(1):168-171.(ZHANG Dong,ZHANG Liaojun,CHEN Chao,et al.Numerical calculation method of force during opening and closing process of high head plane steel gate[J].Water Resources and Power,2014(1): 168-171.(in Chinese))
[ 6 ] 章晋雄,吴一红,张东,等.高水头平面闸门动水关闭的水动力特性数值模拟研究[J].水力发电学报,2013(5):184-190.(ZHANG Jinxiong,WU Yihong,ZHANG Dong,et al.Numerical simulation of hydrodynamics on high-head plane gate[J].Journal of Hydroelectric Engineering,2013(5): 184-190.(in Chinese))
[ 7 ] 王福军.计算流体动力学分析:CFD 软件原理与应用[M].北京:清华大学出版社,2004.
[ 8 ] HIRT C W,NICHOLS B D.Volume of fluid(VOF) method for the dynamics of free boundaries[J].Journal of Computational Physics,1981,39(1): 201-225.
[ 9 ] 郝继光,姜毅,韩书永,等.一种新的动网格更新技术及其应用[J].弹道学报,2007,72(2):88-92.(HAO Jiguang,JIANG Yi,HAN Shuyong,et al.A new dynamic mesh update method and its apllications[J].Journal of Ballistics,2007,72(2): 88-92.(in Chinese))
[10] PANCLIT S M,WU S M.Time series and system analysis with application[M].NewYork: John Wiley & Sons,1983.
[11] 朱学锋,韩宁.基于经验模态分解的非平稳信号趋势项消除[J].飞行器测控学报,2012(1):65-70.(ZHU Xuefeng,HAN Ning.Removal of nonStationary Signal trend items by empirical mode decomposition [J].Journal of Spacecraft TT & Technology,2012(1): 65-70.(in Chinese))[12] 李成业,练继建,刘昉,等.EMD与小波阈值联合滤波方法的改进及其在泄流结构振动分析中的应用[J].振动与冲击,2013(19):63-70.(LI Chengye,LIAN Jijian,LIU Fang,et al.An improved filtering method based on EMD and wavelet-threshold and its application invibration analysis for a flood discharge structure[J].Journal of Vibration and Shock,2013(19): 63-70.(in Chinese))
[13] 徐国宾,訾娟,高仕赵.平面闸门启闭过程中的动水垂直力数值模拟研究[J].水电能源科学,2012(10):132-135.(XU Guobin,ZI Juan,GAO Shizhao.Numerical simulation of hydrodynamics vetical force during plane gate opening and closing process[J].Water Resources and Power,2012(10): 132-135.(in Chinese))
Numericalsimulationofhydrauliccharacteristicsofplaingatewithdifferenttypesofbottomedges
LIU Fang, ZHAO MingLi, LENG Dongsheng, XIN Shiqiang
(StateKeyLaboratoryofHydraulicEngineeringSimulationandSafety,TianjinUniversity,Tianjin300072,China)
The closing process of high-head plain gates was numerically simulated with the RNGk-εmodel, VOF method, and dynamic mesh division technique. The reliability of the numerical method was verified with measured data. The trend term of bottom edge pressure was extracted using empirical mode decomposition (EMD), a processing technology of a nonstationary random process. The relationships between the bottom edge type, flow fluctuation, and holding force were examined. The optimal bottom edge type was determined through comprehensive consideration of the pressure fluctuation, cavitation, and holding force characteristics of the bottom edge. The results show that the type of bottom edges of gates has a significant influence on the opening and closing forces, and a bottom edge with a front inclination leads to the minimum opening and closing forces, lower pressure fluctuation, and less cavitation damage.
plain gate; hydrodynamic closing; numerical simulation; hydrodynamic characteristic; bottom edge type; empirical mode decomposition
国家自然科学基金 (51579172)
刘昉(1979—),男,副教授,博士,主要从事水动力特性研究。E-mail:fangliu@tju.edu.cn
10.3880/j.issn.1006-7647.2017.05.008
TV135.41
:A
:1006-7647(2017)05-0046-05
2016-09-06 编辑:张志琴)
