浅谈教学中创造性思维的培养
2017-09-16江苏省邳州市八义集高级中学王建春
江苏省邳州市八义集高级中学 王建春
浅谈教学中创造性思维的培养
江苏省邳州市八义集高级中学 王建春
在新课程的教育理念下,培养学生积极主动、勇于探索的学习能力已经成为一个重要课题,如何培养学生的创造性思维成为关键。创造性的思维必须有创新意识和创新精神做支撑,这就要求广大教师在新理念的指导下创新教学模式,改革教学方式,提升教学质量,还原教育本质,提升学生的学科核心素养。
创造性思维;独立性;综合性
素质教育要求教育者以人为本,发展个性教育、主动教育、人本教育、创新教育,创新教育是素质教育的时代内涵。在新课改的背景下,教育必须迅速从传统的圈子里走出来,大力推进素质教育,培养青少年学生的创新意识、创新精神、创新能力,进行创新教育。那么在数学教学中,如何培养学生的创造性思维品质呢?下面谈谈我的初步实践和认识。
一、主动发展,培养独立性思维
素质教育的工作重点就是要培养受教育者的创新精神和实践能力。数学学科以其学科特点对学生的独立性思维和主动创新思维有更高的要求,所以在教学实践中要面向全体学生,“让学生主动发展”,有意识地鼓励学生养成独立思维的意识和习惯,敢于发表独立见解,并付诸实践。
比如必修2第32页有这样一道例题:
例1 如图,已知:a∥b,a⊥α求证:b⊥α。

针对这道题目,教材是通过定义法证明线段与平面内的任意一条直线,我在课堂讲解这道例题时,除了应用课本上的方法外,还积极引导学生在学习“线面垂直的判定定理”之后思考其他证明方法。
现把学生的一种证法整理如下:
证明:在平面内作两条相交直线m,n,且m∩n=A。
∵直线a⊥α,
∴a⊥m,a⊥n(由直线与平面垂直的定义知)。
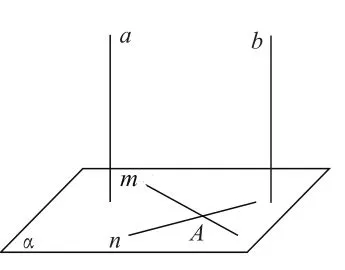
又∵a∥b,
∴b⊥m,b⊥n。
又∵ , ,m∩n=A,
∴b⊥α。
再比如在学习“平面的基本性质”中的公理2“如果两个平面有一个公共点,那么它们还有其他公共点,这些公共点的集合是经过这个公共点的一条直线”时,我随手拿起两本书作为平面模型,让学生体会两个平面的公共点,我故意将其中一本书的端点与另一本书的表面接触,让学生感受到发散思维:两个平面会不会只有一个公共点?这时候学生分组开始讨论。我再利用两张纸演示“平面的无限延伸性”,其中一张纸带有缝隙,再次演示一个交点的情况,顺势将一张纸插到另一张纸的缝隙中,这就会让学生有深刻的印象,培养学生的创造性思维。
二、全面发展,培养综合性思维
数学课堂中要积极培养学生的综合性思维,只有在教学实践中积极运用综合思维,才能提高学生的综合能力和学科素养。
分析:这道题要是直接求解需要从三个方面讨论,这样非常冗繁,此时可以引导学生进行逆向思维,从反面思考,考虑函数图象与x轴的交点均在原点的右侧可得m≥9,其反面为m<9,再考虑Δ≥0,m≠0,可得m的取值范围是m≤1且m≠0(解略)。
思维的“类比推理”是指思维也像数学的“类比推理”一样,寻求事物之间的关系,类比从特殊到特殊。
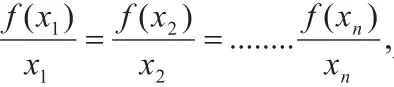
三、创造想象,培养跳跃性思维
爱因斯坦指出:“想象力比知识更重要,因为知识是有限的,而想象力概括着世界上的一切,严格地说,想象力是科学研究中的实在因素。”教师要在民主、平等、轻松的教学情境中,实现创造性的学习活动,并有针对性地进行跳跃性思维的训练。
例如:在正四棱锥O—ABCD中,E,F分别为AD,BC的中点,且OE⊥OB,P为平面OEF与此正四棱锥内切单位球球面的交线上的一动点,求P点到△OEF三个顶点距离平方和的最大值与最小值。
分析:此题分两步考虑。第一步是确定△ABC的形状,第二步是对△OEF内切单位圆上动点求“距离”的最大值与最小值。

猜测:根据经验及题目条件,凭直觉将会预感到这个△OEF是一个等腰直角三角形。通过证明,易得△OEF是等腰直角三角形。之后只要以O为原点,OE,OF为坐标轴建立直角坐标系,问题即趋于明朗化。
教学中,教师把课堂还给学生,相信学生,让学生“先发制人”,大胆直觉、猜想,思维“完美跳跃”,这才是走向成功的捷径。
四、一题多解,培养发散性思维
发散性思维是创造性的思维,要求思维朝着各个方向发散开去,达到流畅、变通、独特。
比如:正三角形两个顶点的坐标是 第三个顶点C在第一象限,求C点坐标。
此题比较简单,但如果能就此例组织一题多解教学,那么,对培养学生的发散性思维能力有促进作用,学生将会受益匪浅。
解法1:方程法。
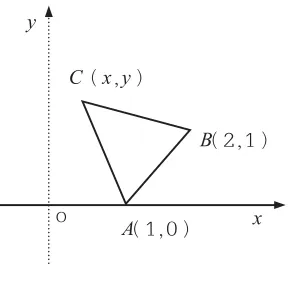
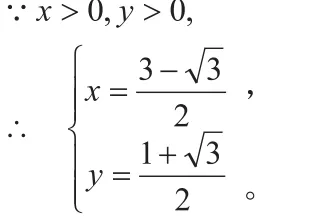
解法2:三角法。
作CD⊥OA, 垂 足 为D, 在 直 角 三 角 形ADC中,于是:

解法3:复数法。
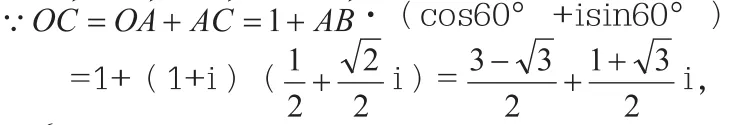
解法4:参数法(理)。
解法5:极坐标法(理)。
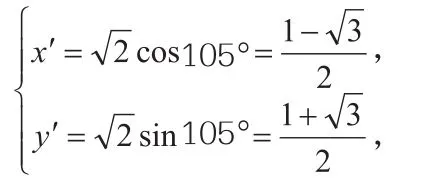
在平时的教学中,教师应帮助学生树立数学精神、求真精神、创新精神,领悟数学的真谛,也许这才是学生受益一生的东西。
