善用韦达定理，提高解题效率

江苏省如皋市第二中学 杨小娟

善用韦达定理，提高解题效率

江苏省如皋市第二中学 杨小娟

韦达定理在高中数学中有诸多应用，无论是解析几何中求两点之间的距离问题、代数问题中求方程根的问题，还是与三角函数相关的问题，应用韦达定理都能起到简化解题过程的作用，学生在学习过程中对这一定理应当加以重视。

两点距离；代数方程；三角函数

韦达定理反映了一元二次方程两根之间的关系，对于某些问题，并不需要求出一元二次方程两个根的具体值，通过韦达定理的应用，就可以解决相关问题，所以韦达定理的应用避免了烦琐的计算，大大提高了解题效率。

一、合理转化，巧求两点距离

对于解析几何中求两点之间距离的问题，直接求点的坐标往往会比较麻烦。如果能够得到相关的方程，通过韦达定理，换一种思路表示出两点之间的距离，则可以使得解题柳暗花明，达到事半功倍的效果。

二、单刀直入，解出方程实根

在解方程的相关问题中，如果题目条件中给出了两根之间的关系，可以联想到使用韦达定理，再结合其他相关的条件，构造出一个新的方程，从而将问题简化。下面的例子就是韦达定理在代数方程问题中的典型应用。

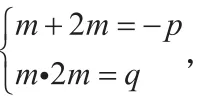
三、紧密联系，解决三角函数问题

数学中的知识相互之间都是紧密联系的，三角函数与方程的根相结合的问题也是非常常见的，对于复合的三角函数问题，直接求解并不可行，若能通过韦达定理将问题进行适当转化，就可以很好地解决相关问题。

例3 已知tanα，tanβ是方程mx2=（2m-3）x+（m-2）=0的两个根，求tan（α+β）的最小值。

解析：由于方程mx2=（2m-3）x+（m-2）=0有两个实根，所以m≠0且Δ≥0，即解得且 m≠0。根据韦达定理，有而tan（α+β）且m≠0，所以等号成立，所以tan（α+β）的最小值为

综上所述，作为高中数学中的一个重要定理，韦达定理在高中数学中的应用非常广泛。应用韦达定理可以大大简化解题过程，将烦琐复杂的问题变得简单直接，同时也可以锻炼学生的数学思维，让学生敢于追求数学的简洁之美。

[1]眭锡坤．应用韦达定理解题的一个问题探讨[J]．数学教学，1992（02）．

[2]肖世安．运用韦达定理解题应注意的问题[J]．中学数学教学参考，2015（21）．