数学课堂中有效的教学设计
2017-09-16江苏省丹阳市云阳学校王红祥
江苏省丹阳市云阳学校 王红祥
数学课堂中有效的教学设计
江苏省丹阳市云阳学校 王红祥
“早改革早收益,晚改革晚收益,不改革不收益。”现在许多学校都在搞教学改革,这肯定是一种趋势,同时也是让大家受益的。随着新课程的改革,教学改革的基本方向为走向自主合作探究的学习,将以往的以“教师为中心,讲授为中心”变为以“学生为中心,学习为中心”的学习模式。在课堂中老师的角色改变了,那么我们怎么样才能获得有效的教学效果呢?课前的教学设计在其中起到的作用必不可少。
把学生的思维充分调动起来,引导学生逐步逼近知识的核心概念、本质内涵、基本原理,达到对知识内部规律的深层次理解,帮助学生真正“学懂”,这是我们教学成功关键的一步,也是我们提高教学质量的核心一环。如何让学生在课堂的学习环节中实现深度学习呢?在初中数学的教学课堂中,有效的教学设计显得非常重要,它能引导学生往学习的深层次发展。
设计有效教学要呈现学习的“主问题”,根据主问题进行针对重难点突破的教学。这就要求我们一线教师要精心地备课,准确地把握每一课的重难点,设计问题要充分体现“问题思维化”,要少问“是什么”,多问“为什么”。
案例1:八(下)第九章《中心对称图形——平行四边形》的复习课的教学案。
原学习内容一:
1.一个菱形的一个内角是60°,其边长为6,那么该菱形的面积是?
2.一个矩形的面积是4,其对角线长为 ,那么其较长的一边长为?
这是两道用以基础训练的小题目,一般是学生先做,然后再交流,最后由学生来讲评,很快就过去了。这样就题论题,学生有的会了,不会的通过同伴教也可能会了,但是我这里要讲的是,如果改变一下条件,那些不会的同学还会不会呢?为什么我们在设计这个问题的时候不能提升一下,让学生彻底搞清晰更深一层的数学方法与思想呢?“授人以鱼,不如授人以渔”,我将它设计如下:
学习内容一:
1.一个菱形的一个内角是60°,其边长为6,那么该菱形的面积是?
同组交流:
问题1:题目的两个条件不变,那么我们还可以求出什么?(结论开放)
问题2:更换条件,但个数不变,你又能求出什么?(条件与结论都开放)
问题3:这说明菱形(矩形)有几个独立的量就可以确定了呢?(维度和基本量的思想)
问题4:正方形有几个基本量就可以确定了?
问题5:根据以上你能否自己编制一些有创意的题目,并让小组成员解决?
问题1、2是学生常见的问题,中等学生完成是没有问题的,它为学生的归纳提炼提供了支撑、依据,问题3是学生思考的航标灯,它为学生的思考指明了方向,它是思想方法的提炼,问题4是方法的迁移,起到举一反三之效果,问题5是结论的应用。每个环节都有特定的任务,而每个问题都能承担特定的功能,串联起来却给人以一气呵成并不断往深处延伸的感觉。可谓小地方也可以深立意,小题目也可派大用场,讲的题目数量少了,但效果好了、品位高了,如果每节课我们都是这样去精心设计和揣摩,何愁教学质量和效果呢?
案例2:在△ABC中,∠ACB=90°,∠ABC=30°,将△ABC绕顶点C顺时针旋转,旋转角为θ(0°<θ<180°),得到△A′B′C。
探究一:
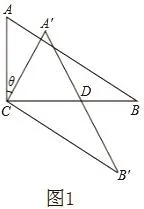
①如图1,当AB∥CB′时,设A′B′与CB相交于点D。求证:△A′CD是等边三角形。
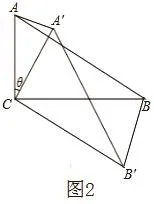
②如图2,连接AA′、BB′,设△ACA′ 和△BCB′ 的面积分别为S△ACA′和S△BCB′。求证:S△ACA′∶S△BCB′=1∶3。
探究二:
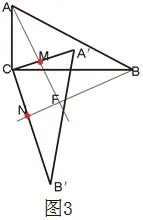
如图3,取A′C ,B′C的中点M、N,设直线AM与BN相交于点F, 求∠AFB的度数和AM∶BN的值。
探究三:
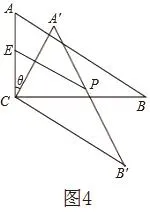
如图4,设AC中点为E,A′B′中点为P,AC=a,连接EP,当θ=______时,EP长度最大,最大值为___________。
设计分析:它是旋转问题,这是几种变换中的重点,也是历年来中考的热点。笔者通过探究一的一个预热过程很好地帮学生复习了有关旋转的基本知识,探究二是笔者自编的旋转与相似相结合的一道探究题,是为让学生结合问题生成变化过程,时刻联系我们学过的所有几何方法并灵活应用,探究三是探究的高潮,学生可以通过三角形两边之和大于第三边来做,是画出点P运动的轨迹,从而发现当点E、C、P共线时,EP最长。过程中,笔者努力营造一种民主、平等、和谐的课堂氛围,积极鼓励学生参与学习,鼓励质疑问难,发表不同意见,使每位学生不用担心自己的意见被批评,而是坚信自己的观点是受欢迎的。这样,学生讨论起来才心无疑虑,才能互相启发,取长补短,不同层次的学生才能各有发展。同时,多注重情感投入,加强师生的情感沟通。新课程有效教学的最终目的是:彻底改变学生的学习方式,实现学生的有效学习。研究表明,每个人同时具有多种智能,并以不同的方式表现出来。这给我们的启发是课堂上应当让学生选择适合自己的学习方式,让每个人都参与到课堂中来,发挥每个人的智能特长。
我们提倡教师在课堂上要尽可能地给学生多一点思考的时间,多一点活动余地,多一点表现自己的机会,多一点体验成功的愉快,促使学生不断掌握学习方法,逐步从“学会”到“会学”,最后达到“好学”的美好境界。