提高相位干涉仪测角精度新方法

王克让，李娟慧，朱晓丹，张广宇， 朱伟强

(中国航天科工集团8511研究所,江苏 南京 210007)

·技术前沿·

提高相位干涉仪测角精度新方法

王克让，李娟慧，朱晓丹，张广宇， 朱伟强

(中国航天科工集团8511研究所,江苏 南京 210007)

为进一步提高传统相位干涉仪测角精度，提出一种利用所有基线信息的新测角方法。在给出该测角方法的基础上，分析了该方法的测角精度。理论分析表明该方法测角精度优于传统方法，可适用于一维和二维线阵，且不改变现有阵列的布阵形式，算法计算量小。仿真结果验证了理论分析的正确性，且在低信噪比情况下，该方法测角性能提高更加明显。

电子侦察；相位干涉仪；测角精度；线阵

0 引言

电子侦察是现代电子战中必不可少的重要组成部分，其中目标角度参数具有相对的稳定性，是进行信号分选和识别的重要参数。对目标角度参数的测量主要有振幅法、比相法、空间谱估计等方法，相位干涉仪[1-4]测向作为比相法的一种，具有测向精度高、实时性好、技术相对简单和工程上易于实现等优点，在电子侦察测向[1]中得到了广泛的应用。在军事领域，相位干涉仪可对雷达、通信、测控、敌我识别等辐射源进行测向定位，能在实施针对性电子干扰和军事打击中发挥重要作用；在民用领域，它可用于交通管制、生命救援、无线电频谱管理等诸多方面。

相位干涉仪测向体制利用不同通道的相位差估计辐射源方向，为了提高测角精度，干涉仪一般采用多基线的方式，即使用长基线测向保证测角精度[5]，短基线解模糊，整个系统的测角精度取决于最长基线长度。为了进一步提高测角精度，理论上可继续加大基线长度，但是加大基线长度必然造成通道数多,设备体积、质量和功耗的进一步加大，设备成本的升高。而且在一些应用平台中，如机载、星载[6]等对载荷设备的体积、质量和功耗有着严格的限制，不可能无限制地加大基线长度来提高测向精度。

本文提出一种充分利用干涉仪多基线信息的测向方法，该方法不影响原干涉仪的布阵方式和解模糊方法，也不增加基线长度，可有效提高测向精度。

1 提高测角精度方法

(1)

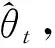
(2)

(3)

(4)

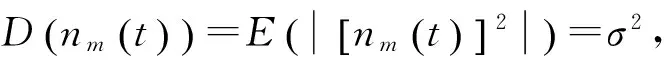
(5)

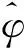
(6)

式中，λ为信号波长。

因此，当相位干涉仪布阵设计完成后，可选择的基线个数M也就确定了，本文方法仅比传统方法多了算式(5)，因此基本不增加算法的计算量。

2 理论分析

(7)

可写为：

φt

(8)

式中，φt可称之为归一化相位差，其误差直接传递到目标角度的估计。为了比较本文和传统方法角度估计精度，可以通过比较归一化相位差得到，由式(6)可知本文的归一化相位差φ为：

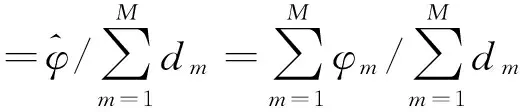
(9)

由于nm为相互独立的零均值高斯噪声，则式(9)方差为:

(10)

传统方法的归一化相位差方差为：

(11)

则：

(12)

下面采用归纳法证明式(12)不大于1，即证明式(13)成立。

(13)

当M=1时，式(13)显然成立；

(14)

即式(13)成立；

假设M=K-1时式(13)成立，下面证明M=K时式(13)也成立，K为变量，根据式(13)有：

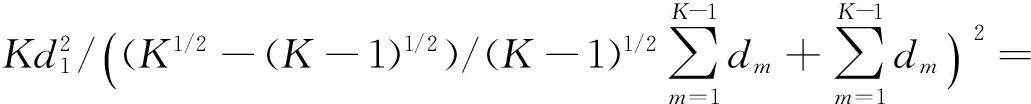
(15)

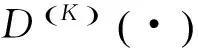
3 仿真

仿真对比实验1：

为了说明本文测角精度较传统干涉仪算法的优越性，做如下仿真实验。干涉仪由4个阵元组成3基线干涉仪，3基线长度分别为0.1m、0.15m、0.225m，如图1所示。假设辐射源频率为8GHz，所在角度为69°。本文方法和传统方法估计的角度均方根误差与相位差误差之间的关系如图2所示。

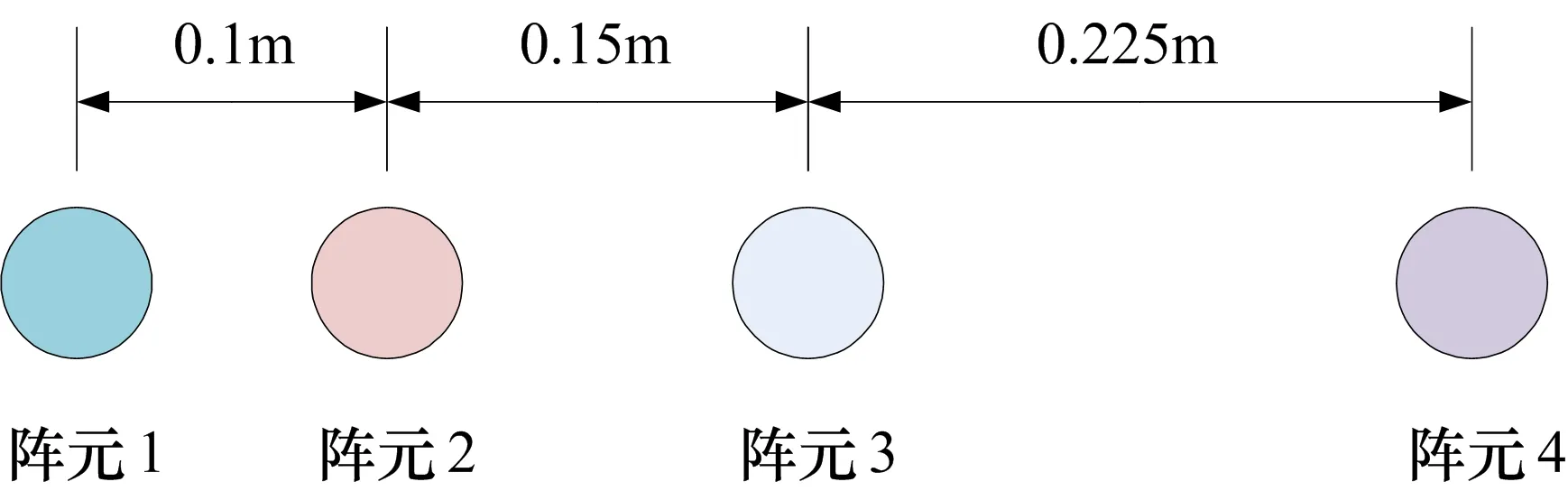
图1 一种3基线天线布阵方式

图2 一维阵角度估计误差与相位误差关系曲线图

从图2可知，本文方法角度估计误差要小于传统方法，且随着相位误差的增大，本文方法提高性能越明显；同时本文并没有对阵列布阵方式有额外的要求，仅要求能够正确解模糊，阵列适应性较广；此外，一旦阵列形式确定以后，在测角时本文测角方法仅比传统方法多出一步计算，算法简单，运算量小。

仿真对比实验2：

本实验的相位干涉仪为L形状的二维干涉仪，每维3基线共7个阵元(其中1个阵元共用)，其中方位维的布阵方式与实验1相同，俯仰维布阵方式的基线比为2∶3∶10，其3个基线长度分别为0.05m、0.075m、0.25m，如图3所示。假设辐射源频率为8GHz，辐射源方位角和俯仰角角度分别为69°和20°，那么把二维干涉仪分为2个一维干涉仪，方位维本文方法和传统方法估计的角度均方根误差与相位差误差之间的关系如图4(a)所示，俯仰维本文方法和传统方法估计的角度均方根误差与相位差误差之间的关系如图4(b)所示。

图3 一种二维L形天线布阵方式

图4 二维阵方位角度估计误差与相位误差关系曲线图

对比图4(a)和图2可知，实验1和实验2结果一致，这是由于本次实验的方位维布阵方式、目标角度与实验1相同。从图4(b)可知，本文方法角度估计误差小于传统方法，且随着相位误差的增大，本文方法性能提高越明显。这说明本文方法不仅能够提高定位精度，而且还适合二维阵列相位干涉仪。

4 结束语

在电子侦察中，相位干涉仪是一种重要的测向装备。本文提出一种相位干涉仪测向方法，可以充分利用干涉仪的多条基线信息，从而提高测角精度。该方法仅比传统方法增加一步求和计算，具有计算量少的优点，且可适应一维和二维线阵，可不改变现有布阵方法。因此，本文方法无论是对改造升级传统相位干涉仪装备还是对设计新装备都具有重要参考价值。■

[1] 吴奉微, 程婷, 贾可新, 等. 基于虚拟阵列变换的干涉仪测向算法[J]. 现代雷达， 2012，34(3)：42-49.

[2] Schmieder L，Mellon D，et al．Interference cancellation and signal direction finding with low complexity[J]．IEEE Trans. on AES，2010，46(3):1052-1063．

[3] Liu Tingting，Xiao Ling．About the ambiguities in DOA estimation[J]．Chinese Journal of Electronics，2010，19(4):747-751．

[4] 韩月涛, 潘伟萍, 吴嗣亮,等. 干涉仪解模糊异常值检测及纠错方法[J]. 北京理工大学学报, 2012, 32(8):849-854.

[5] 石荣, 阎剑, 张聪. 干涉仪相位差测量精度及其影响因素分析[J]. 航天电子对抗, 2013, 29(2):35-38.

[6] 李腾, 郭福成, 姜文利. 星载干涉仪无源定位新方法及其误差分析[J]. 国防科技大学学报, 2012, 34(3):164-170.

A novel improving angle accuracy method for phase interferometer

Wang Kerang, Li Juanhui, Zhu Xiaodan, Zhang Guangyu,Zhu Weiqiang

(No.8511 Research Institute of CASIC, Nanjing 210007, Jiangsu,China)

In order to further improve the angle accuracy of the traditional phase interferometer, a novel measuring angle method using all baseline information is introduced. The angle accuracy of the method is analyzed theoretically. The analysis shows that the angle accuracy of the method without extra computational loads is superior to that of the traditional method. The proposed method is suitable for 1D and 2D linear array without changing the array form of the existing array. Simulation results verify the correctness of the propose method, and the accuracy of the method is more obvious in the case of low SNR.

electronic reconnaissance; phase interferometer; angle accuracy; linear array

2017-05-16；2017-06-26修回。

王克让(1983-)，男，高工,博士，主要研究方向为电子侦察总体技术。

TN971

： A