我国财政教育支出的趋势ARIMA模型

(云南财经大学 云南 昆明 650000)

我国财政教育支出的趋势ARIMA模型

朱峰亿

(云南财经大学云南昆明650000)

随着我国经济的快速发展，政府对教育投入规模不断扩大。本文基于1952-2015年财经教育支出的数据，利用趋势ARMA模型，对我国未来几年的教育支出进行了定量预测。预测结果显示：我国财政教育支出大致呈现指数增长趋势。

时间序列；教育支出；平稳性；趋势ARMA模型；预测

一、研究背景与文献综述

在当今世界，知识经济已成为占主导地位的经济形态，整个教育事业的发展水平和发展质量关系到国民经济的发展水平和国家综合国力的提高，关系到社会主义现在化建设的全局和未来，教育事业必须摆在优先发展的战略地位。

世界各国尤其是发达国家为在国际经济竞争中争取主动权，纷纷把推动人才教育作为国家发展战略，大幅度提高教育投入。我国政府亦明确提出，实现长期可持续发展要依靠科技进步和劳动素质的提高，要深入实施科教兴国战略和人才强国战略。科技进步的核心因素是教育，随着经济的发展，我国的教育投入经费也在快速增长。

现代国内有关教育投资的文献很多，研究的角度也各不相同，如：李艳、刘锐、武志鸿、刘惠生等研究的角度是纵向比较我国教育支出经费情况，揭示我国教育投资的现状以及存在的问题；王莹、陈平等主要从政府教育投资与经济增长的关系进行研究的，进而揭示教育投资对经济增长的促进。

从上述研究来看，由于采用的数据以及时间跨度不同、数学模型和计量方法的差异，得出的结果不尽相同。因财政教育支出受经济基础、人口、环境等诸多因素的影响，这些因素之间由有着错综复杂的关系，运用结构性的因果模型分析和预测其值往往比较困难，所以，本文在借鉴诸位专家学者的基础上，结合本人所学的时间序列知识，从历年的数据出发，拟合趋势—ARMA模型分别来预测未来我国财政教育支出的趋势。

二、趋势ARMA模型的基本思想

ARMA(p,q)模型，是一类常用的随机时序模型，它是一种精度较高的时间序列预测方法。其基本思想是：某些时间序列是依赖于时间t的一族随机变量，构成该时序的单个序列值虽然具有不确定性，但整个序列的变化却有一定的规律可以用相应的数学模型近似描述。通过都该数学模型的分析，能够更本质的认识时间序列的结构和特征，达到最小方差意义下的最优预测。在现实生活中，我们常常运用ARMA(p,q)模型对经济体进行预测和分析，得到较为满意的效果。

而在自然界中，由确定性因素导致的非平稳通常显示出非常明显的规律性，比如有显著的趋势或者有固定的变化周期，这种规律性通常比较容易提取，而由随机因素导致的波动则非常难以确定、分析。根据这种性质，传统的时序分析方法通常都把分析的重点放在确定性信息的提取上，忽视对随机信息的提取，将序列简单地假定为：

Xt=μt+εt

式中，{εt}为零均值白噪声序列。这种分析方法就称为确定性分析方法。

当预测对象依时间变化呈现某种上升或下降的趋势，并且无明显的季节波动，又能找到一条合适的函数曲线反映这种变化趋势时，可以以时间t为自变量，该时间序列为因变量，建立趋势模型：

Yt=f(t)+μt

模型中的f(t)包含了反映各种主要因素对Yt长期变化趋势的影响，残差项ut既反映Yt的长期趋势中随机波动的影响，又包含构成Yt预测模型的主要因素之外的其他因素的影响。f(t)的函数形式取决于时间序列本身的变化规律和所采用的的预测方法，它常常表现为线性回归、指数函数、多项式和一些特定的函数。在用传统方法得到f(t)的估计后，利用时间序列分析，再对产生的残差项ut建立ARMA(p,q)模型，这样就构成了有趋势的时间序列模型：

其中，εt为服从正态分布的白噪声序列。

从理论上讲，趋势ARMA模型比单一的ARMA模型的预测效果好，这是由于它既包含了可由时间变量t解释的Yt的那部分，又包含了时间变量不可解释的但可由ARMA模型解释的Yt的变差的另一部分。因此建立趋势ARMA模型的方法，简单地说就是选用最小二乘按照某类函数拟合数据序列的确定性部分，即先将趋势(线性或指数)性拟合提出，建立其趋势方程，然后将残差序列建立合适的ARMA(p,q)模型。

三、我国财政教育支出的趋势-ARMA模型的建立

(一)数据的来源

本文的选取的指标是国家财政教育支出(单位：亿元)。数据全部来自中国统计年鉴和中国国家统计局。本文样本为时间序列数据，统计区间选择1952-2015年，包括64个观测值。

图1 1952-2015我国财政教育支出序列

由上图可见，从整体上看出，我国财政教育支出呈逐年上升趋势，不具有明显的周期变化和季节波动。且从1952年至1990年间，上升趋势较缓慢，从1990年至2015年，上升趋势较剧烈。

(二)趋势项的估计

从图1原始序列的时序图可以看出，我国的财政教育支出大致呈现曲线增长的趋势，所以对其进行曲线形式的拟合。

采用R语言中的回归拟合命令对序列进行二次型模型拟合。从输出结果可以得到，我国财政教育支出序列的拟合模型为：

Yt=abt,t=1,2,……64

将模型取对数为：

LnYt=Lna+Lnbt,t=1,2,…,64

同样采用R语言进行指数型模型拟合。输出结果得出，按指数型模型拟合的我国财政教育支出的趋势模型为：

LnYt=1.9738+0.1124t+εt

还原为指数模型为：

Yt=7.1980*1.1190t+eεt

拟合图如下：

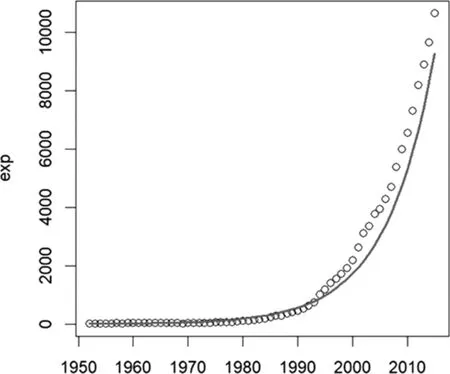
(三)残差序列ARMA模型拟合和白噪声检验

对残差序列进行ARMA模型拟合，采用R语言auto.arima命令自动定阶，输出结果显示，模型为ARIMA(3,1,2)，模型表达式为：

▽εt=-0.4068εt-1-0.7932εt-2+0.2418εt-3+μt+0.8834μt-1+0.8490μt-2

模型的检验主要是检验模型的有效性。若是白噪声，则接受选择的模型；否则，要重新进行模型识别、定阶、估计、检验。现仍然采用LB统计量对拟合的ARIMA(3,1,2)模型进行残差序列的白噪声检验：

表1 白噪声检验结果

从检验结果中看出，残差序列延迟6期和延迟12期的LB统计量的P值均显著大于显著性水平0.1。说明残差序列是一个白噪声，模型拟合效果良好，可以认为该模型是可取的，能用于接下来的预测。

(四)趋势ARMA模型的预测

趋势ARMA模型的预测需要分为两部分预测，一部分为确定的趋势模型的预测，另一部分为残差项的预测，最后将预测值相加。利用上文建立的趋势ARMA模型对2016-2020年的我国财政教育支出进行预测，预测结果如下：

表2 模型的预测结果

(单位：亿元)

四、结论

本文采用趋势ARMA模型我国财政教育投资进行了短期预测。总的来说，本文时间序列模型的建立与实际值拟合效果良好，预测结果较为精准。结果显示，我国财政教育支出呈逐年上升趋势，表明我国对教育事业的重视程度越来越高。

尽管本文结果不能完全代表现实，但对我国教育事业蒸蒸日上的今天，我们把握教育支出的趋势具有较好的借鉴意义。

[1]王燕.时间序列分析[M].北京:中国人民出版社

[2]我国财政教育支出时间序列预测——基于ARMA模型

[3]李艳,刘锐.我国目前人力资本现状分析及对策[J].经济研究.2006.11

[4]武志鸿,刘惠生.中国人力资本投资现状、问题和调整思路[J].内蒙古煤炭经济.2001.05

[5]王莹.政府教育投资与经济增长分析[J].财贸经济.2000.06

[6]陈平.中国人力资本投资与经济增长的关系[J].经营与管理.

朱峰亿(1992-)，男，汉族，四川宜宾人，云南财经大学统计与数学学院，研究方向：数量经济学。