拓扑Hausdorff维数的一种计算方法及其应用

饶 峰， 柯 枫

(1.湖北商贸学院 基础课部， 湖北 武汉 430079; 2.湖北大学 数学与统计学院， 湖北 武汉 430062)

拓扑Hausdorff维数的一种计算方法及其应用

饶 峰1，2， 柯 枫2

(1.湖北商贸学院 基础课部， 湖北 武汉 430079; 2.湖北大学 数学与统计学院， 湖北 武汉 430062)

介绍平面上集合的拓扑Hausdorff维数的一种计算方法，此方法是根据集合的几何特征构造它的一个基，利用基的边界的Hausdorff维数获得该集合的拓扑Hausdorff维数.利用此方法计算了一类分形方块的拓扑Hausdorff维数.

Hausdorff维数; 拓扑维数; 拓扑Hausdorff维数; 分形方块

1 预备知识

在本文中，度量空间X的Hausdorff维数[1]记为dimHX，拓扑维数[2]记为dimtX.dimH∅=dimt∅=-1.拓扑Hausdorff维数是最近由R.Balka等[3]提出来的一种新的维数，它是结合Hausdorff维数与拓扑维数的概念产生的,具有一些好的性质，在分形研究中日益受到关注.

定义 1.1[3]令dimtH∅=-1.非空度量空间X的拓扑Hausdorff维数为dimtHX=inf{d:X有一个基U使得对任意的U∈U都有dimH∂U≤d-1}，其中∂U表示集合U的边界.

从定义不难看出一个非空空间的拓扑Hausdorff维数是0或至少为1.拓扑Hausdorff维数具有单调性;对闭集具有可数稳定性;是双Lipschitz不变量[3].下面的2条性质将在本文中用到.

性质 1.2[3]对任意的度量空间X，有dimtX≤dimtHX≤dimHX.

由此性质可知一个有限集或可数集的拓扑Hausdorff维数为0.

性质 1.3[3]X是一个非空可分度量空间，那么dimtH(X×[0，1])=dimH(X×[0，1])=dimHX+1.

拓扑Hausdorff维数不是由拓扑维数及Hausdorff维数决定的，即存在2个紧度量空间X和Y，虽然dimtX=dimtY，dimHX=dimHY，但dimtHX≠dimHY[3]，因此计算集合的拓扑Hausdorff维数是有意义的.

2 基的构造

维数的计算一直是分形几何研究的热点.本节介绍一种拓扑Hausdorff维数的计算方法.此方法是根据集合的几何结构构造出它的一个拓扑基，确定基的边界的Hausdorff维数，由定义1.1得到该集合的拓扑Hausdorff维数上界，再由集合的特征确定下界.如果上下界相同，则获得该集合的拓扑Hausdorff维数.此方法的关键是构造集合的基，先给出基的判别定理.

定理 2.1[4]设U是拓扑空间(X，T)的一个开集族，则U是拓扑空间X的一个基，当且仅当对于每一个x∈X和x的每一个邻域Ux，存在Vx∈U使得x∈Vx⊆Ux.

定理 2.2 设F是R2中的子空间，开集族U如上所述，则W={U∩F:U∈U}是F的一个基.

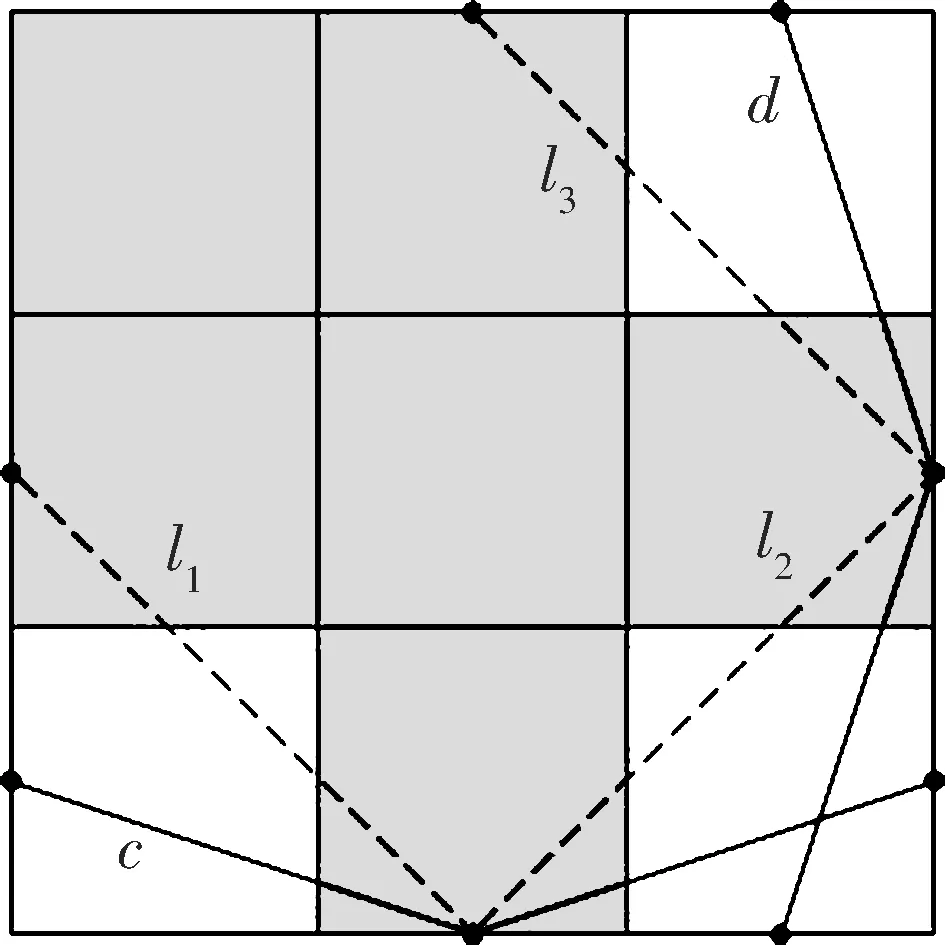
证明 对任意p∈F和p的任意邻域Up⊂F，当|m|，n足够大时，在{cnm}和{dnm}中分别存在2条折线，这4条折线围成一个多边形区域V，使p∈V，V∩F⊂Up，由定理2.1可知定理成立.

3 分形方块维数的计算

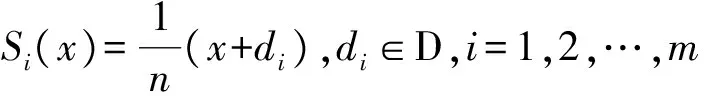
分形方块的形成与三分Cantor集类似:第一步，按照给定的D，将单位正方形[0，1]2等分为n2个小正方形，留下m个(留下的小正方形在本文图中涂黑);第二步，将留下的每个小正方形按第一步方式再等分成n2个小正方形后留下m个;如此反复下去，最后得到的极限集就是由n和D确定的分形方块F.

本节主要计算F3，6中连通分形方块的拓扑Hausdorff维数，图1是F3，6中10个连通分形方块，有下面结论:

定理 3.1 F3，6中连通分形方块的拓扑Hausdorff维数都为1.为后面叙述的方便，先介绍符号空间和编码等概念.

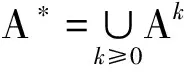
下面计算图1中连通方块的拓扑Hausdorff维数，即证明定理3.1.

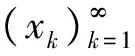
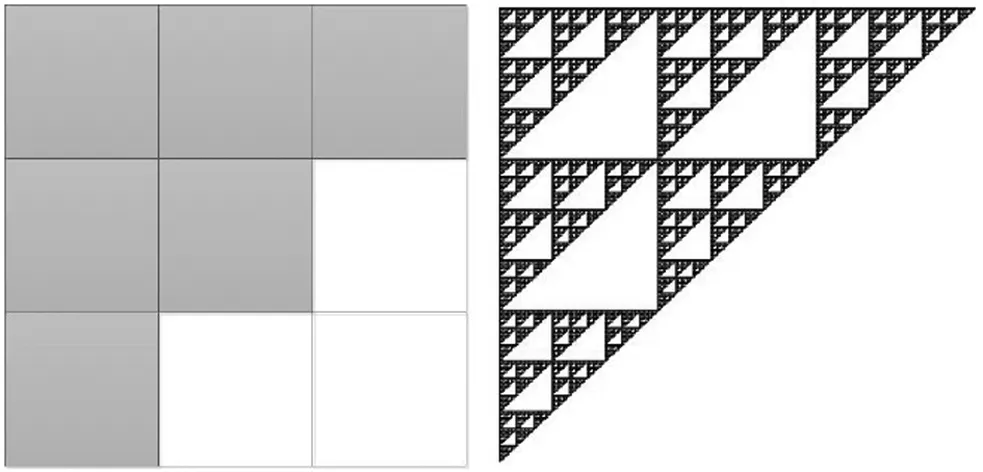
(a) F1

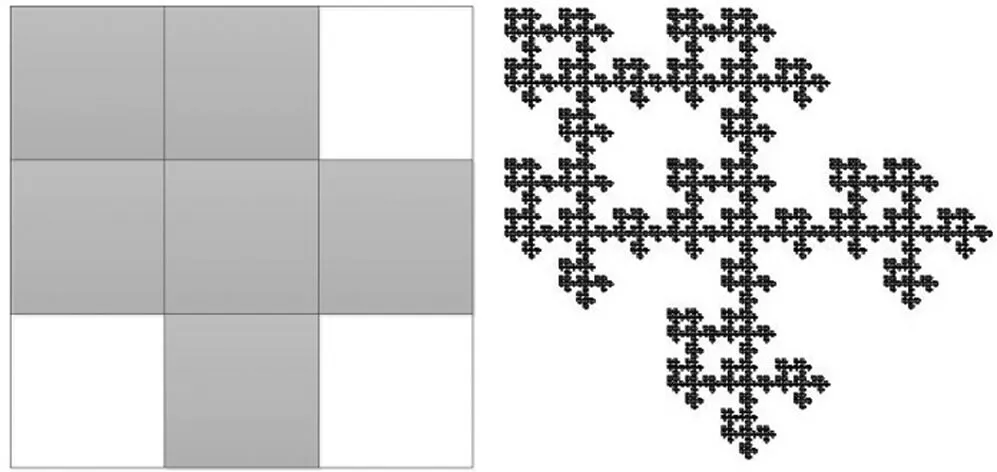
(b) F2

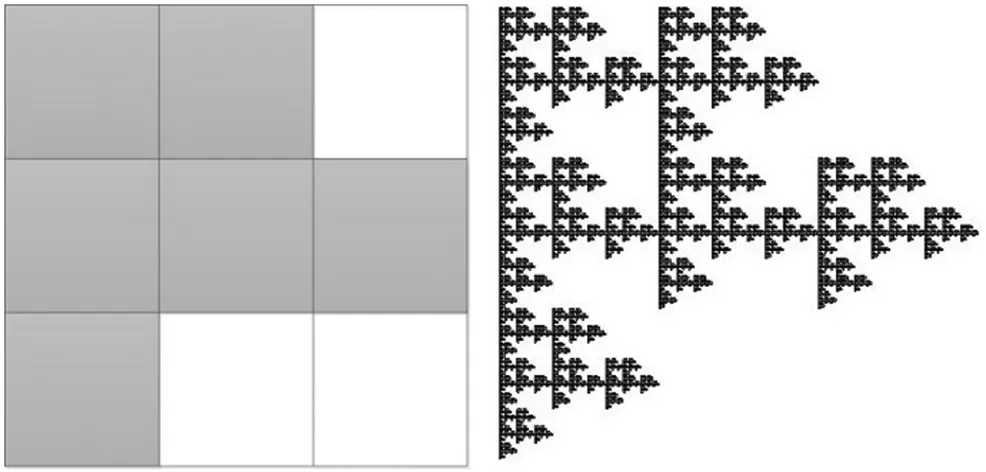
(c) F3

(d) F4

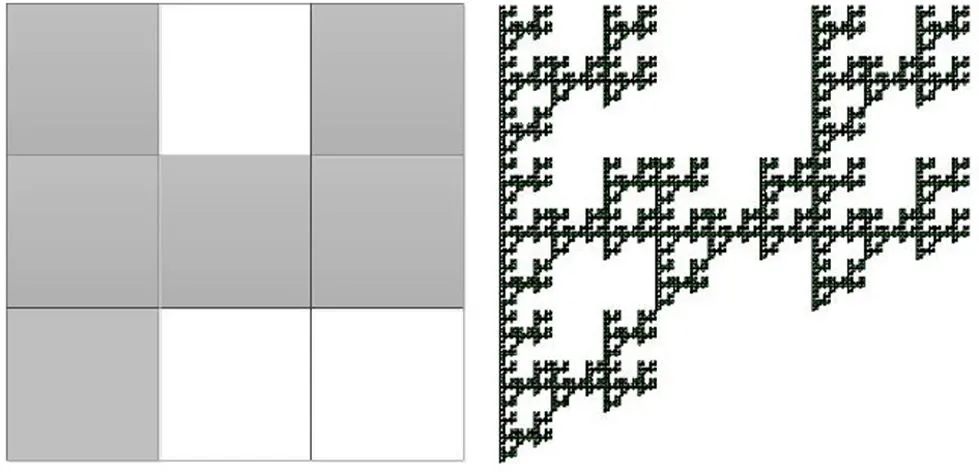
(e) F5

(f) F6

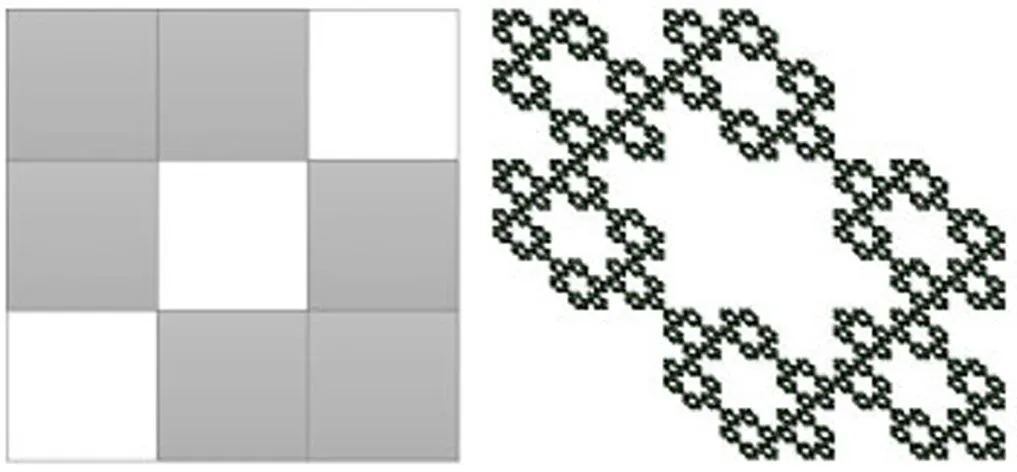
(g) F7

(h) F8

(i) F9

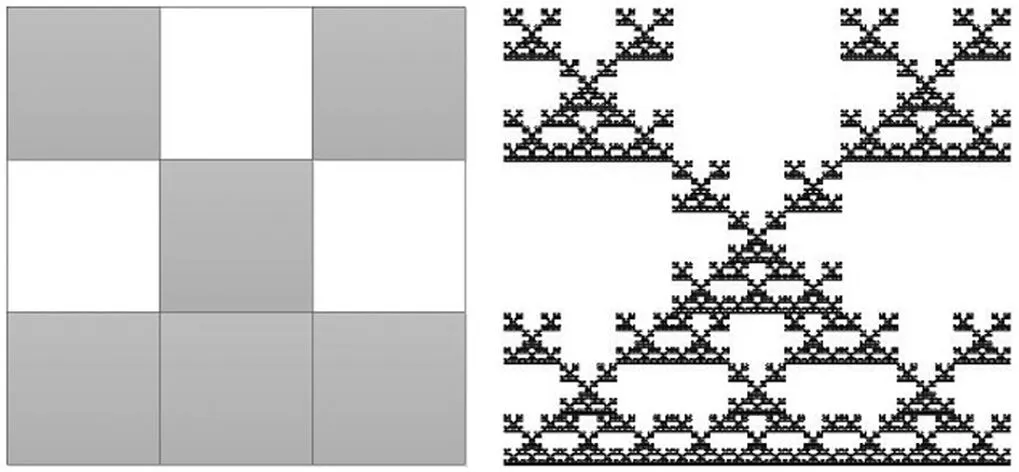
(j) F10

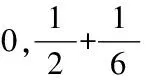
(a)

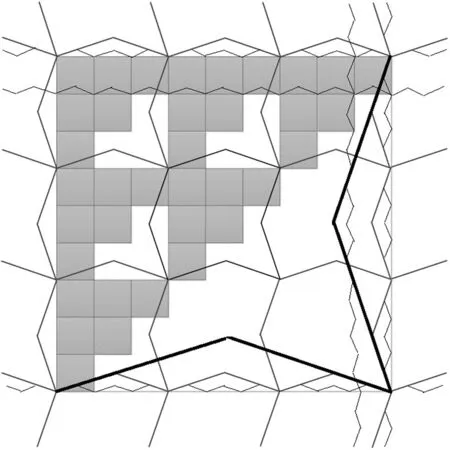
(b)

构成F1的基.由于折线cnm、dnm与F1只交于有限个点，所以∂(U∩F1)是由有限个点构成的，dimH∂(U∩F1)≤0.由定义1.1知dimtHF1≤1.又因为F1包含线段l，由性质1.2知dimtHF1≥1.故dimtHF1=1.

从以上过程可以发现根据集合的几何特征构造折线段c，d是关键，利用它们就可以构造分形方块的基.在后面先构造剩下9个分形方块中的折线段c，d，再一起说明它们的拓扑Hausdorff维数为1.

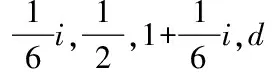
(a) F2

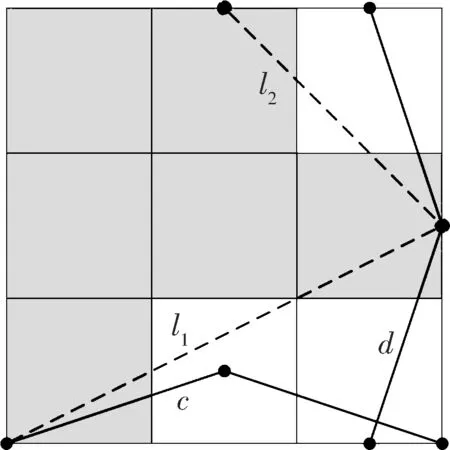
(b) F3

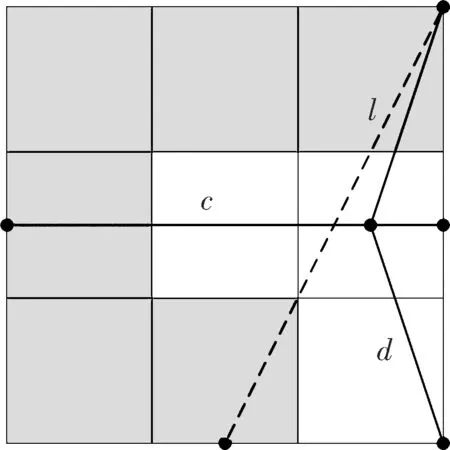
(c) F4

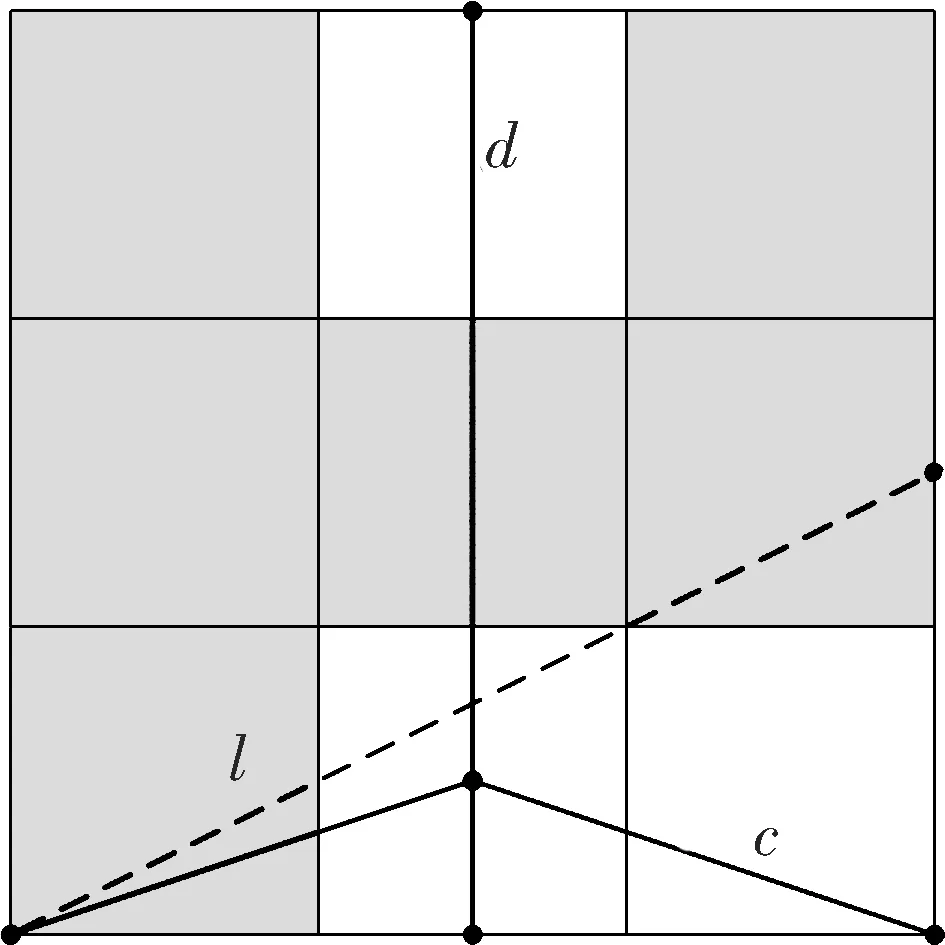
(d) F5

(e) F6

(f) F7

(g) F8

(h) F9

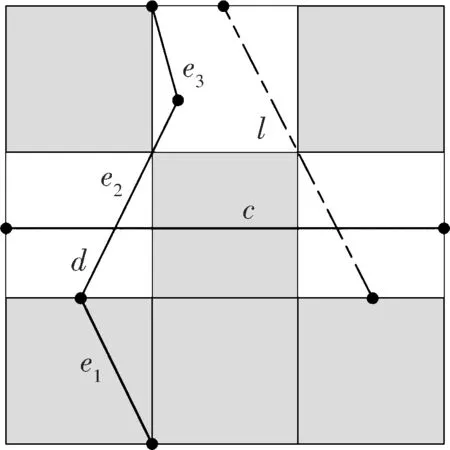
(i) F10

分形方块F4的数字集

D4={d1，d2，d3，d4，d5，d6}=

分形方块F5的数字集

D5={d1，d2，d3，d4，d5，d6}=

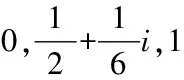
分形方块F6的数字集

D6={d1，d2，d3，d4，d5，d6}=

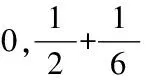
分形方块F7的数字集

D7={d1，d2，d3，d4，d5，d6}=

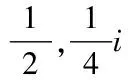
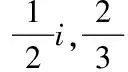
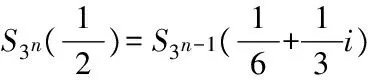
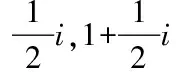
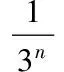
4 问题及展望

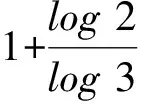
[1] FALCONER K J. Fractal Geometry:Mathematical Foundations and Applications[M]. 2nd. England:John Wiley,2003:31-119.

[2] HUREWICZ W, WALLMAN H. Dimension Theory[M]. Princeton:Princeton Uiversity Press,1948:12-20.

[3] BALKA R, BUCZOLICH Z, ELEKES M. A new fractal dimension:the topological Hausdorff dimension[J]. Adv Math,2015,274(1):881-927.

[4] 熊金城. 点集拓扑讲义[M]. 北京:高等教育出版社,2011:82-83.

[5] BALKA R. Inductive topological Hausdorff dimensions and fibers of generic continuous functions[J]. Monatsh Math,2014,174(1):1-28.

[6] BALKA R, BUCZOLICH Z, ELEKES M. Topological Hausdorff dimension and level sets of generic continuous functions on fractals[J]. Chaos Solitons Fractals,2012,45(12):1579-1589.

[7] BALKA R, FARKAS A, FRASER J M, et al. Dimension and measure for generic continuous images[J]. Ann Acad Sci Fenn Math,2013,38:389-404.

[8] MAULDIN R D, WILLIAMS S C. On the Hausdorff dimension of some graphs[J]. Trans Am Math Soc,1986,298(2):793-803.

[9] HYDE J T, LASCHOS V, OLSEN L, et al. On the box dimensions of graphs of typical continuous functions[J]. J Math Anal Appl,2012,391(2):567-581.

[10] FALCONER K J. On the Hausdorff dimension of distance sets[J]. Mathematika,1985,32(2):206-212.

[11] WHYBURN G T. Topological characterization of the Sierpiński curve[J]. Fund Math,1958,45(6):1090-1099.

2010 MSC: 28A80; 54F45

(编辑 陶志宁)

A Calculation Method of the Topological Hausdorff Dimension and Its Applications

RAO Feng1,2， KE Feng2

(1.FundamentalCourseDepartment,HubeiBusinessCollege,Wuhan430079,Hubei; 2.SchoolofMathematicsandStatistics,HubeiUniversity,Wuhan430062,Hubei)

A calculation method of the topological Hausdorff dimension of a set on a plane is introduced. This method is to construct a basis of the set and then use Hausdorff dimension of the boundary of the basis to obtain the topological Hausdorff dimension of this set. We calculate the topological Hausdorff dimensions of a class of fractal squares by this method.

Hausdorff dimension; topological dimension; topological Hausdorff dimension; fractal square

2016-08-24

湖北省教育厅科学技术研究项目(B2016480)

饶 峰(1977—)，男，讲师，主要从事分形几何的研究，E-mail:601682168@qq.com

O189

A

1001-8395(2017)04-0496-07

10.3969/j.issn.1001-8395.2017.04.012