广义神经传播方程新的非协调混合元方法的超逼近分析

张厚超, 毛凤梅, 白秀琴

(平顶山学院 数学与统计学院, 河南 平顶山 467000)

广义神经传播方程新的非协调混合元方法的超逼近分析

张厚超, 毛凤梅, 白秀琴

(平顶山学院 数学与统计学院, 河南 平顶山 467000)

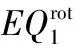
广义神经传播方程; 非协调混合元方法; 半离散及全离散格式; 超逼近

1 预备知识

考虑文献[1]广义神经传播方程的初边值问题

(1)

其中,Ω⊂R2是具有Lipschitz连续边界的有界凸多边形区域,∂Ω为Ω的光滑边界,T∈(0,+∞)为一定值,X=(x,y),u0(X)、u1(X)是充分光滑的已知函数,f(u)、g(u)均为有界函数,且满足对变量u的Lipschitz连续条件.

众所周知,混合有限元方法是有限元领域中最活跃的分支之一,被广泛应用于微分方程的有限元分析[13-14].与传统Galerkin方法相比,混合有限元方法具有对空间要求光滑度较低,并能同时得到原始变量和中间变量的误差估计等优势.该方法对广义神经传播方程的应用也受到较多关注,文献[15-16]分别研究了广义神经传播方程的H1-Galerkin混合元格式和修正的H1-Galerkin混合元方法,都得到了半离散格式下的原始变量和相应中间变量的最优误差估计.文献[17]利用Q00+span{1,x,y,y2}×span{1,x,y,x2}元给出了广义神经传播方程的一个低阶非协调混合元格式,得到了相关变量的最优误差估计.但是,以上研究均是基于传统的混合元格式,有的以投影作为分析的必要工具[16].近年来,文献[18-19]针对二阶椭圆问题提出了一种新的混合元格式,较之传统混合元具有空间对匹配更容易满足离散的BB条件,自由度少,且可以避免对矢量有限元空间的试探函数进行散度运算等优点.目前,这种格式已被广泛应用于二阶椭圆问题[20]、抛物方程[21]和Sobolev方程[22]的高精度分析.

2 混合有限元的构造及性质

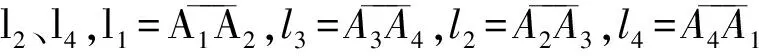
定义混合有限元空间

Vh={vh;vh|K∈span{1,x,y,x2,y2},

对于u∈H1(Ω),w∈(H1(Ω))2,设Ih:H1(Ω)→Vh和Πh:(L2)2→Wh分别为由Vh和Wh诱导的插值算子,满足:Ih|K=IK,Πh|K=ΠK及

(2)

和

其中n是对应边li,i=1,2,3,4的单位外法向量.

下面给出几个引理,它们在后面的误差分析中有重要作用.

引理 2.1[23]若p∈(H2(Ω))2有

(3)

引理 2.2[24]若u∈(H1(Ω))有

(4)

引理 2.3[25]若p∈(H2(Ω))2有

(5)

3 半离散格式及超逼近分析

为了构造问题(1)的混合元格式,引入中间变量p=-(▽ut+▽u),则问题(1)等价于

(7)

其中(u,v)=∫Ωuvdxdy.

考虑(7)式的半离散格式为:求{uh,ph}:[0,T]→Vh×Wh,使得

(8)

定理 3.1 问题(8)的解存在且唯一.

(8)式可表示为如下的等价形式

(9)

其中

因为矩阵C是对称正定矩阵,由(9)式的第一和二式可得

(10)

(10)式是一个关于向量H(t)的微分方程,且A是对称正定的,由注意到F是Lipschitz连续的,由常微分方程解的理论知[26]:当t>0时,H(t)存在且唯一,进而H(t)存在且唯一,即问题(8)存在唯一解.证毕.

下面先讨论上述问题的超逼近性质.

定理 3.2 设{u,p}和{uh,ph}分别是(7)和(8)式的解,u,ut,utt∈H2(Ω)∩W1,∞,p∈(H2(Ω))2,则

(11)

(12)

证明 令u-uh=(u-Ihu)+(Ihu-uh)η+ξ,p-ph=(p-Πhp)+(Πhp-ph)ρ+θ,由(7)和(8)式可得下面的误差方程

在(13)式中令vh=ξt,wh=▽ξt,得

(14)

注意到(14)式左端可表示为

下面依次估计Ai,i=1,2,…,6.

利用Schwarz不等式及Young不等式,可得

根据假设f(·),g(·)是Lipschitz连续的,则有

根据引理2.2的第一式,可得

A4=A5=0.

利用导数转移技巧以及引理2.3,则有

将上述关于Ai,i=1,2,…,6的估计以及(15)式代入(14)式,并由引理2.2的第二式,可得

(16)

对(16)式两端都乘以2,再从0到t积分,并利用ξt(0)=0,ξ(0)=0及Gronwall引理可得

(17)

由(11)式得证.

在(13)式中令vh=ξtt,Wh=▽ξtt,得

(18)

下面对(18)式右端各项进行估计,类似于Ai,i=1,2,…,5的估计,则有

B5=B6=0.

利用导数转移技巧以及引理2.3,则有

将上述对Bi,i=1,2,…,7的估计代入到(18)式,则有

将上式两端都乘以2,然后从0到t积分,并注意到ξt(0)=0,▽ξt(0)=0,利用(17)式,则有

由Fubini定理知

将其代入到(19)式,然后利用Gronwall不等式得

(20)

(21)

利用Schwartz不等式及Young不等式以及引理2.2,容易验证

将对Di,i=1,2,…,5的估计、(17)和(20)式代入(21)式得

定理得证.

4 全离散格式及超逼近分析

下面给出问题的全离散逼近格式,并进行误差分析.

问题(7)的全离散等价表示形式为

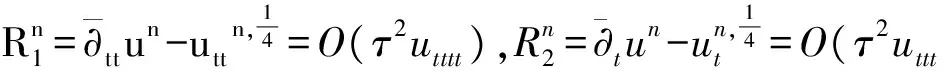
定义(22)式的全离散逼近格式:求{Un,Pn}∈Vh×Wh,使得

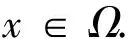
(23)

为了进行误差估计,引入如下记号:

由(22)和(23)式,∀vh∈Vh,Wh∈Wh,可得

定理 4.1 设{u(tn),p(tn)}和{Un,pn}分别是问题(23)和(24)的解,假设u∈L∞(0,T;H2(Ω)),ut,utt∈H2(Ω),uttt∈L∞(0,T;H1(Ω)),uttt∈L∞(0,T;L2(Ω)),p∈L∞(0,T;H2(Ω))有

Ch2F1+Cτ2F2,

(25)

其中

(26)

(26)式的左端可表示为

(27)

对(26)式右端各项进行估计,注意到

则有

根据引理2.2的第一式得

E2=E3=0.

接下来估计E4,先将E4分裂为下面3项,然后分别进行估计.

根据假设知f(·)是有界的,由Schwarz不等式有

同理可得

注意到∀i=1,2,…,n-1有

(28)

综合E4j,j=1,2,3的估计以及(28)式和引理2.2的第二式,则有

根据引理2.3得

将(27)式及上述对Ei,i=1,2,…,8的估计代入到(26)式,然后两端从1到J,J=1,2,…,n-1,求和得

(29)

根据引理2.2的第二式知

(31)

在(31)式中取适当小的τ,使得1-Cτ>0,然后利用离散的Gronwall不等式,则有

(32)

(33)

根据(33)式可得

利用引理2.1以及引理2.2的第一式,容易验证

G4=G5=0.

类似于E8的估计,可得

将上述对Gi,i=1,2,…,6的估计代入(33)式并取充分小的ε,可得

(34)

定理得证.

注 4.1 容易验证,通过利用文献[21]中构造的插值后处理算子,可以得到相应的超收敛结果.值得一提的是,文献[27]利用文献[28-29]的协调混合元,对f(u)=f(X)的特殊情况,在全离散格式下得到了原始变量H1模意义下的超逼近和超收敛结果以及中间变量p的最优误差估计.而本文利用非协调混合元对方程(1)得到了上述变量的超逼近结果,本文的分析结果是对文献[27]以及文献[6-11]的延伸和扩展.

[1] PAO C V. An mixed initial boundary value problem arising in neurophysicology[J]. J Math Anal Appl,1975,52(1):105-119.

[2] 梅茗. 高维广义神经传播方程Cauchy问题整体光滑解[J]. 应用数学学报,1991,14(4):450-461.

[3] 万维明,刘亚成. 神经传播方程初边值问题解的长时间行为[J]. 应用数学学报,1999,22(2):311-315.

[4] 崔霞. 广义神经传播方程的A.D.I.有限元分析[J]. 应用数学学报,1999,22(4):628-633.

[5] 那顺布和. 一类神经传播方程的特征差分方法和最佳L2误差估计[J]. 生物数学学报,2009,24(3):470-478.

[6] 吴志勤,王芬玲,石东洋. 广义神经传播方程一个新的超收敛估计及外推[J]. 数学的实践与认识,2011,41(15):234-240.

[7] 王萍丽,史艳华,石东洋. 广义神经传播方程的超收敛估计及外推[J]. 西北师范大学学报(自然科学版),2012,48(1):22-25.

[8] 王萍丽,石东洋. 广义神经传播方程非协调类Wilson元的超收敛分析及外推[J]. 生物数学学报,2013,28(4):672-680.

[9] 张斐然,石东洋,陈金环. 广义神经传播方程的非协调变网格有限元方法[J]. 应用数学学报,2012,35(3):471-482.

[10] 石东洋,郝颖. 广义神经传播方程的一个各向异性非协调有限元超收敛分析[J]. 生物数学学报,2009,24(2):279-286.

[11] 郭志林,陆风玲. 一类非线性广义神经传播方程的非协调元超收敛分析[J]. 湖南师范大学(自然科学学报),2011,34(6):1-5.

[12] 乔保民,梁洪亮. 一类非线性广义神经传播方程Adini元超收敛分析[J]. 山东大学学报,2011,46(8):42-46.

[13] VIDER THOMEE. Galerkin Finite Element Methods for Parabolic Problems[M]. 2nd ed. Berlin:Spring-Verlag,2006.

[14] LIN Q, LIN J F. Finite Element Methods:Accuracy and Improvement[M]. 北京:科学出版社,2006.

[15] 石东洋,周家全. 广义神经传播方程一个新的H1-Galerkin非协调混合有限元格式[J]. 河南师范大学学报(自然科学版),2010,38(5):1-6.

[16] 曹京平,刘洋,何斯日古楞,等. 广义神经传播方程的一种修正混合有限元方法的误差分析[J]. 数学的实践与认识,2011,41(24):234-2239.

[17] 马戈,石东洋. 广义神经传播方程的一非协调混合有限元方法[J]. 数学的实践与认识,2010,40(4):217-223.

[18] 陈绍春,陈红如. 二阶椭圆问题新的混合元格式[J]. 计算数学,2010,32(2):213-218.

[19] 史峰,于佳平,李开泰. 椭圆方程的一种新型混合有限元格式[J]. 工程数学学报,2011,28(2):231-237.

[20] 石东洋,李明浩. 二阶椭圆问题一种新格式的高精度分析[J]. 应用数学学报,2014,37(1):45-58.

[21] 石东洋,张亚东. 抛物型方程一个新的非协调混合元超收敛分析与外推[J]. 计算数学,2013,35(4):337-352.

[22] 史艳华,石东洋. Sobolev方程新混合元方法的高精度分析[J]. 系统科学与数学,2014,34(4):452-463.

[23] 林群,严宁宁. 高效有限元构造与分析[M]. 保定:河北大学出版社,1996.

[24] SHI D Y, YU C P, CHEN S C. Superconvergence of a nonconforming finite element approximation to Viscoelasticity type equations on anisotropic meshes[J]. 高等学校计算数学学报(英文版),2006,15(4):375-384.

[25] SHI D Y, MAO S P, CHEN S C. Anisotropic nonconforming finite element with some superconvergence results[J]. J Comput Math,2005,23(3):261-274.

[26] JACK K. HALE. Ordinary Differential Equations[M]. New York:Wiley-Inter-Science,1969.

[27] 樊明智,王芬玲,石东洋. 广义神经传播方程最低阶新混合元格式的高精度分析[J]. 山东大学学报,2015,50(8):77-89.

[28] 石东洋,张厚超. 一类非线性四阶双曲方程扩展的混合元方法的超收敛分析[J]. 计算数学,2016,38(1):65-82.

[29] 张厚超,石东洋. 非线性四阶双曲方程低阶混合元方法的超收敛分析[J]. 数学物理学报,2016,36(4):656-671.

2010 MSC：65N15; 65N30

(编辑 郑月蓉)

Superclose Estimates Analysis of a New Mixed Finite Elements Method for Generalized Nerve Conduction Equation

ZHANG Houchao, MAO Fengmei, BAI Xiuqin

(SchoolofMathematicsandStatistics,PingdingshanUniversity,Pingdingshan467000,Henan)

Based on the nonconformingEQrot1element and the Raviart-Thomas(R-T) element, a new lower order nonconforming mixed finite elements method is proposed for Generalized nerve conduction equation. Firstly, the existence and uniqueness of approximation solutions are proved. Secondly, based on the high accuracy results of the about two elements and derivative transferring technique with respect to the time variable, the superclose with orderO(h2) for the primitive solution inH1-norm and the intermediate variablepinL2-norm are obtained under semi-discrete scheme respectively. Finally, a new fully-discrete approximation scheme is proposed and the superclose estimates with orderO(h2+τ2) are deduced for the primitive solution inH1-norm and the intermediate variablepinL2-norm respectively. Here,handτare the subdivision parameter in space and time step respectively.

generalized nerve conduction equation; nonconforming mixed finite elements method; semi-discrete and fully-discrete schemes; superclose

2016-10-05

国家自然科学基金(11271340)和河南省科技计划项目(162300410082)

张厚超(1980—),男,讲师,主要从事有限元方法及应用的研究,E-mail:zhc0375@126.com

O242.21

A

1001-8395(2017)04-0464-09

10.3969/j.issn.1001-8395.2017.04.006