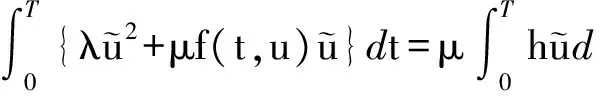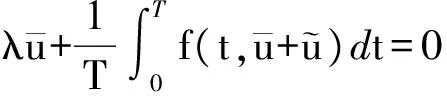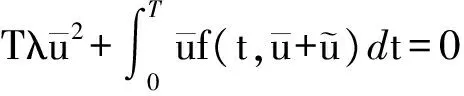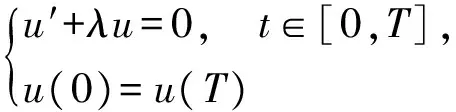非线性一阶周期边值问题解的分歧结构

2017-09-15马陆一闫东亮李晓燕

四川师范大学学报（自然科学版） 2017年4期

关键词：李晓燕边值问题时滞

马陆一, 闫东亮, 李晓燕

(西北师范大学数学与统计学院, 甘肃兰州 730070)

非线性一阶周期边值问题解的分歧结构

马陆一, 闫东亮, 李晓燕*

(西北师范大学数学与统计学院, 甘肃兰州 730070)

利用分歧理论和解集连通理论,研究非线性一阶周期边值问题

分歧理论; 一阶周期边值问题; 多解性

1 引言及主要结果

一阶周期边值问题在经济学、生态学等研究领域中有丰富的实际应用背景.近年来,许多学者对该类问题进行了广泛研究.例如:1980年,W.S.Gurney等[1]建立了一个绿蝇繁殖模型,该模型可由如下一阶微分方程刻画

2004年,PengS.G.[2]运用锥拉伸与锥压缩不动点定理在一定条件下获得一阶周期边值问题

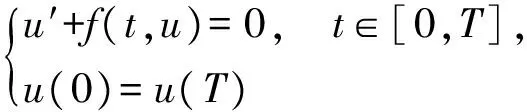
正解的存在性结果,其中f∈C([0,T]×R,R),并且存在常数M>0,使得当t∈[0,T]时,Mt-f(t,u)≥0.2004年,WangH.Y.[3]利用锥拉伸与锥压缩不动点定理,研究了一阶带时滞微分方程

u′(t)=a(t)g(u(t))u(t)-

λb(t)f(u(t-τ(t))),t∈R,

并获得正周期解的存在性与多解性结果.对于这类一阶时滞微分方程,Ma R. Y.等[4]作了进一步的研究.

1990年,J. Mawhin等[5]运用分歧理论和解集连通理论,在一定条件下证明了非线性二阶周期边值问题

(1)

解的个数在λ=0附近的变化情况:∀λ∈(-∞,1),问题(1)至少有一个解;当λ<0且靠近0时,问题(1)至少有3个解.

受以上文献的启发,一个值得思考的问题是:一阶周期边值问题

(2)

能否建立起类似的解的存在性结果?

本文将运用分歧理论和解集联通理论建立类似于二阶情形下的结果,即在适当条件下确定：当λ在0附近变化时,问题(2)解的个数的变化情况.由于二阶微分算子是对称算子,而一阶微分算子非对称,所以一阶周期边值问题解的存在性的研究会遇到一些新的困难,需要创新和改变.

本文假设:

(C2) f∈C([0,T]×R,R),且存在γ∈C[0,T]使得|f(t,u)|≤γ(t);

(C3) 存在一个常数R>0,使得|u|≥R时有f(t,u)u>0成立.

定理 1 假设(C1)～(C3)成立,则存在λ+,λ->0,当λ∈[0,λ+]时,该问题至少有一个解;当λ∈[-λ-,0)时,该问题至少有3个解.

2 预备知识

设Y={u∈C1[0,T]∶u(0)=u(T)}为范数‖u‖Y=max{‖u‖∞,‖u′‖∞}下构成的Banach空间,C:=C[0,T].

定义算子L:Y→C,Lu=u′-u,容易验证L可逆.因此线性问题

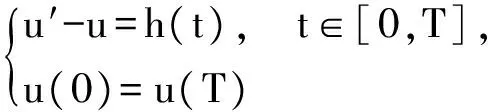
(3)

有唯一解,则问题(2)可以转化成

u=-L-1(λ+1)u+L-1[h(t)-f(t,u)],

其中L-1:C→Y为紧算子,且当‖u‖→∞时,

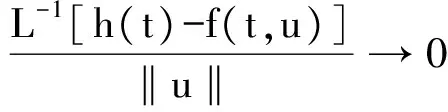
3 主要结果的证明

为了证明主要结果,首先给出以下3个引理.

设E为一个实Banach空间,F:E×R→E为一个全连续映射,考虑方程

u-F(u,λ)=0.

(4)

引理 3.1[5]假设存在E中的有界开集O,使得

deg(I-F(·,a),O,0)≠0.

则存在(4)式的解集连通分支C1和C2,并且

C1⊂E×(-∞,a]∩(I-F)-1(0),

C2⊂E×[a,∞)∩(I-F)-1(0).

当C=C1或C=C2时,有以下结论成立:

1)C∩O×{a}≠Ø;

2)C有界或者C∩EO×{a}≠Ø.

引理 3.2[5]定义O=BR(O)={u∈E:‖u‖a,使得当a≤λ≤b时有‖u‖0,使得当b≤λ≤b+δ时存在(u,λ)∈C2且满足‖u‖≤2R.

当λ在a的左侧时可以得到类似的结论.

引理 3.3 假设(C1)～(C3)成立,则存在R0>0,使得当λ≥0时,问题(2)存在一个解u,并且‖u‖

证明考虑问题(2)的同伦族问题

(5)

由Leray-Schauder原理可知,若(5)式的所有可能解都有一个先验界,则问题(2)存在一个解.显然这个解有界.下面证明(5)式解的先验界的存在性.

假设0<δ≤λ,令

(6)

其中

对(5)式两边从0到T积分得

在等式两边同时乘以1/T,则

可推得

化简得

(7)

由于

所以

(7)式可以化简为

结合条件(C2)和(C3)可知

因此

令

则

对(5)式两边从0到T积分并取μ=1得

因此

定理1的证明由于在∂R0上问题对应的算子方程没有不动点,由拓扑度的同伦不变性可知当λ≥0时,

deg(I-h(·,λ),O,0)≠0.

由引理3.1和3.2的结论,当λ≥0时,存在一个解的连通分支C,并且C延伸到λ=0的左侧.

另一方面,λ=0是

的主特征值,由文献[6]中关于分歧问题的方法,在λ=0侧有解的连通分支从无穷远处产生.分歧产生的解的连通分支C具有以下性质:∀ε>0,存在(u,λ)∈C,使得当|λ-0|<ε时,有‖u‖>1/ε成立.而根据之前的证明,由于当λ≥0时,问题(2)的所有可能解都有界,若连通分支从λ=0的右侧产生,则出现矛盾.因此,解的连通分支从λ=0的左侧产生.由文献[6]的结论可知,若λ<0并且靠近0,一定从无穷远处产生两条解的连通分支C+与C-,并且有以下结论成立:

若R<1/ε,即ε<1/R时,∀-1/R<λ<0,可以获得两个解u+和u-,其中u+∈C+,u-∈C-,并且‖u‖>R.再结合解的连通分支C,一定存在λ->0,使得λ∈[-λ-,0)时,问题(2)至少有3个解.

所以当假设(C1)～(C3)成立时,存在λ+,λ->0,当λ∈[0,λ+]时,问题(2)至少有一个解;当λ∈[-λ-,0)时,问题(2)至少有3个解.

[1] GURNEY W S, BLYTHE S P, NISBET R N. Nicholson’s blowflies revisited[J]. Nature,1980,287(5777):17-21.

[2] PENG S G. Positive solutions for first order periodic boundary value problem[J]. Appl Math Comput,2004,158(2):345-351.

[3] WANG H Y. Positive periodic solutions of functional differential equations[J]. J Diff Eqns,2004,202(2):354-366.

[4] MA R Y, CHEN R P, CHEN T L. Existence of positive periodic solutions of nonlinear first-order delayed differential equations[J]. J Math Anal Appl,2011,384(2):527-535.

[5] MAWHIN J, SCHMITT K. Nonlinear eigenvalue problems with the parameter near resonance[J]. Ann Polon Math,1990,51(1):241-248.

[6] RABINOWITZ P H. On bifurcation from infinity[J]. J Diff Eqns,1973,14(3):462-475.

[7] BEREANU C, MAWHIN J. Upper and lower solutions for periodic problems:first order difference vs first order differential equations[C]//Inter Conf Math Anal Appl. Craiova:AIP,2005:23-24.

[8] SUN J P, LI W T. Existence of solutions to nonlinear first-order PBVPs on time scales[J]. Nonlinear Anal,2007,67(3):883-888.

[9] LIU X, LI W. Existence and uniqueness of positive periodic solutions of functional differential equations[J]. J Math Anal Appl,2004,293(1):28-39.

[10] WU Y. Existence of positive periodic solutions for a functional differential equation with a parameter[J]. Nonlinear Anal,2008,68(7):1954-1962.

[11] 张露,刘瑞宽. 一阶时滞微分方程正周期解的存在性[J]. 四川师范大学学报(自然科学版),2014,37(5):649-652.

[12] 朱雯雯,徐有基. 带非线性边界条件的一阶微分方程多个正解的存在性[J]. 四川师范大学学报(自然科学版),2016,39(2):226-230.

[13] MA R Y. Existence and uniqueness of solutions to first-order three-point boundary value problems[J]. Appl Math Lett,2002,15(2):211-216.

[14] LIU B. Existence and uniqueness of solutionsto first-order multipoint boundary value problems[J]. Appl Math Lett,2004,17(11):1307-1316.

[15] CHEN R P, MA R Y, HE Z Q. Positive periodic solutions of first-order singular systems[J]. Appl Math Comput,2012,218(23):11421-11428.

[16] 谭亮,钟守铭. 一类具有离散时滞和分布时滞的BAM神经网络的全局耗散分析[J]. 四川师范大学学报(自然科学版),2017,40(1):11-17.

[17] NIETO J J, RODRIGUEZ-LOPEZ R. Existence and approximation of solutions for nonlinear functional differential equations with periodic boundary value conditions[J]. Comput Math Appl,2000,40(4):433-442.

2010MSC：34B15

(编辑周俊)

Bifurcation Structure of Nonlinear First-order Periodic Boundary Value Problems

MA Luyi, YAN Dongliang, LI Xiaoyan

(CollegeofMathematicsandStatistics,NorthwestNormalUniversity,Lanzhou730070,Gansu)

In this paper, we use bifurcation theory and continuation theory to show the multiplicity results for first-order periodic boundary value problem