区间直觉模糊支付合作对策的核仁
2017-09-15董立伟温晓楠
董立伟, 修 春, 温晓楠
(1. 北京交通大学 海滨学院, 河北 黄骅 061100; 2. 河北农业大学 基础课部, 河北 保定 071000)
区间直觉模糊支付合作对策的核仁
董立伟1, 修 春1, 温晓楠2*
(1. 北京交通大学 海滨学院, 河北 黄骅 061100; 2. 河北农业大学 基础课部, 河北 保定 071000)
在考虑支付值为区间直觉模糊集问题的基础上,对合作对策的核仁进行推广.在已知区间直觉模糊集的得分函数和精确函数及其排序方法的基础上,建立区间直觉模糊支付合作对策模型,并提出区间直觉模糊核仁的概念,给出区间直觉模糊支付合作对策的核仁与核心、稳定集之间的关系,讨论区间直觉模糊支付合作对策核仁的特征和性质.
区间直觉模糊集; 模糊合作对策; 字典序; 核仁
1981年J. P. Aubin[1]提出模糊合作对策,之后其理论得到了越来越广泛的研究与应用.在合作对策中,最受关注的问题是总联盟的收益如何才能公平合理的分配,即求对策的解.面对这个问题人们给出了许多形式的解[2-4],其中包括核心和稳定集、核仁和预核仁、Shapley值和Owen值等,其中核心和稳定集是常用的集合形式的解,但可能为空,Shapley值是常用的单值形式的解,Owen值是基于联盟结构的解.D. Schmeidler[5]提出的核仁解的定义,不仅弥补了核心和稳定集可能为空这一缺陷,且这种解是由唯一的一个分配构成.
但在实际对策问题中,参与人的判断存在一定的犹豫度的现象是普遍的.K. T. Atanassov等[6-7]把模糊集理论推广到直觉模糊集和区间直觉模糊集,并定义了一些基本的运算规则.目前的研究主要集中在徐泽水[8]的多属性决策和郭菊花等[9]研究的直觉模糊对策.本文在具有区间直觉模糊支付的合作对策模型下,建立核仁的概念及相关理论,并对其性质进行讨论.
1 预备知识
1.1 区间直觉模糊集
定义 1 设X是一个给定论域,则A是一个区间直觉模糊集
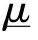
定义 2 设X是非空集合,X=(x1,x2,...,xn),A、B为区间直觉模糊集,且

3) A∩B={〈x,[min(a1,a2),min(b1,b2)],[max(c1,c2),max(d1,d2)]〉|x∈X};
4) A∪B={〈x,[max(a1,a2),max(b1,b2)],[min(c1,c2),min(d1,d2)]〉|x∈X}.
1.2 区间直觉模糊集IIFS的排序方法
定义 3 设α={〈x,[a,b],[c,d]〉|x∈X}是一个区间直觉模糊数,则称:


定义 4 设α1、α2为任意2个区间直觉模糊数,则:
1) 若S(α1) 2) 若S(α1)=S(α2),则H(α1)=H(α2),α1=α2;H(α1) 定义 6 设IIFΓ为区间直觉模糊合作对策,称 为IIFΓ的分配集. 其中 即 用≥L或者≤L来表示字典序. 2) 由得分函数和精确函数的定义3知 同理 (1) 1≤i≤2N-1, 取Ω′⊂Ω,|Ω′|=i,则 从而 因此,由定义9知 (2) (3) 唯一性用反证法证明,设 并且 从而 (4) 如果 则 由(5)式有 从而 (6) 不难证明 由(6)式有 所以 取 则 本文主要研究支付值为区间直觉模糊集的模糊合作对策问题,通过文献[10]中定义的IIFS的得分函数和精确函数概念及给出的新的排序方法,构造区间直觉模糊合作对策模型,定义其核心、核仁等概念,并证明了直觉模糊合作对策核仁的存在性和唯一性,以及核仁与核心、稳定集的关系. [1] AUBIN J P. Cooperative fuzzy game[J]. Mathematics of Operations Research,1981,6(1):1-13. [2] CHUN Y. On the symmetric and weighted shapley values[J]. International J Game Theory,1991,20(2):183-190. [3] BRANZEI R, DIMITROV D, TIJS S. Models in Cooperative Game Theory[M]. Berlin:Springer-Verlag,2008. [4] 高作峰,徐东方,鄂成国. 重复模糊合作对策的核心和稳定集[J]. 运筹与管理,2006,15(4):68-72. [5] SCHMEIDLER D. The nucleolus of a characteristic function game[J]. SIAM J Appl Math,1968,17(6):1163-1170. [6] ATANASSOV K T. Intuitionistic fuzzy sets[J]. Fuzzy Sets and Systems,1986,20(1): 87-96. [7] ATANASSOV K T. Intuitionistic Fuzzy Sets[M]. Berlin:Springer-Verlag,1999. [8] 徐泽水. 区间直觉模糊信息的集成方法及其在决策中的应用[J]. 控制与决策,2007,22(2):215-219. [9] 郭菊花,高作峰. 直觉模糊支付合作对策的核心[J]. 系统科学与数学,2014,34(4):420-430. [10] 王坚强. 模糊多准则决策方法研究综述[J]. 控制与决策,2008,23(6):601-606. [11] 张晓玲,高作峰. 效用可转移的模糊族对策[J]. 辽宁工程技术大学学报(自然科学版),2015,34(10):1196-1200. [12] LI D F, NAN J X. A nonlinear programming approach to matrix games with payoffs of atanassov’s intuitionistic fuzzy sets[J]. Int J Uncertainty, Fuzziness and Knowledge- based Systems,2009,17(4):585-607. [13] 邹正兴,李登峰,何云. 基于风险偏好和满意度的区间值合作对策[J]. 运筹与管理,2015,24(6):34-43. [14] 温晓楠,董立伟. 重复模糊合作对策的核仁[J]. 长春大学学报,2012(8):980-982. [15] 张盛开,张亚东. 对策论与决策方法[M]. 大连:东北财经大学出版社,2000. [16] 高作峰,王友,王国成. 对策理论与经济管理决策[M]. 北京:中国林业出版社,2006. 2010 MSC:03E72 (编辑 郑月蓉) Nucleolus of Interval Intuitionistic Fuzzy Payoffs Cooperative Game DONG Liwei1, XIU Chun1, WEN Xiaonan2 ( 1.HaibinCollege,BeijingJiaotongUniversity,Huanghua061100,Hebei; 2.BasicCourseDepartment,HebeiAgriculturalUniversity,Baoding071000,Hebei) Based on the problem of payoffs for interval intuitionistic fuzzy sets, in this paper we generalize the nucleolus of cooperative game. For given score function, accurate function and their approach for rangking of IIFS, the cooperative game model and the concept of the fuzzy nucleolus are founded. Further, we give the relations among nucleolus, core and stable set, and discuss the characteristics and properties of interval intuitionistic fuzzy cooperative games. interval intuitionistic fuzzy set; fuzzy cooperative game; lexicographic order; the nucleolus 2016-08-12 河北省高等教育学会基金(GJXH2013-189) O225 A 1001-8395(2017)04-0473-05 10.3969/j.issn.1001-8395.2017.04.007 *通信作者简介:温晓楠(1985—),女,讲师,主要从事概率论和对策论的研究,E-mail:304968792@qq.com2 区间直觉模糊支付合作对策模型



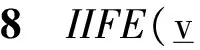





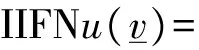

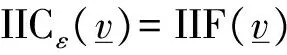
3 主要结论及证明



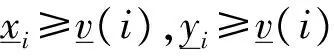

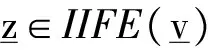

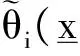
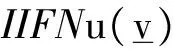



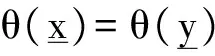

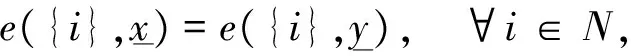






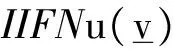
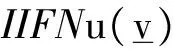







4 结束语
