零和自由半环上的半可逆矩阵

龙艳华, 王学平

(1. 成都大学 师范学院, 四川 成都 610106； 2. 四川师范大学 数学与软件科学学院, 四川 成都 610066)

零和自由半环上的半可逆矩阵

龙艳华1, 王学平2*

(1. 成都大学 师范学院, 四川 成都 610106； 2. 四川师范大学 数学与软件科学学院, 四川 成都 610066)

在零和自由半环上,举例说明矩阵方程组AX=B和X+A1B=A2B并不是在所有情况下都同解,其中A是已知的n×n阶半可逆矩阵,X是未知的n维列向量,A1和A2分别满足条件I+AA1=AA2和I+A1A=A2A.得到关于方程AX=B和X+A1B=A2B同解的一些条件,完善零和自由半环上半可逆矩阵的相关性质,扩展矩阵的应用范围.

零和自由半环; 交换半环; 半可逆矩阵; 线性方程组； 方程组的解

1 基本概念及预备知识

矩阵是重要的数学工具,在信息理论、不确定信息处理、图像处理、计算智能和群体决策等方面有着广泛应用,如文献[1-9].半环上的矩阵理论也在最优化理论、运筹学、自动化控制、离散事件网络与图论的模型方面有许多应用,如文献[5,10-15]，其中,半环上的可逆矩阵是一类重要的矩阵.1952年,R. D. Luce[16]讨论了布尔代数(一种特殊的半环)上的布尔矩阵,证明了矩阵可逆当且仅当它是一个正交矩阵[15].从此以后,半环上可逆矩阵的理论便得到了广泛研究,如文献[4,17-18].特别地,Zhao C.K.[19]得到了在Brouwer格上矩阵可逆的必要条件和充分条件,Han S.C.等[20]给出了坡矩阵可逆的一些充分必要条件,Tan Y.J.[21]考虑了交换零和自由半环(亦称为反环[21])上的可逆矩阵,得到了矩阵可逆的一些充要条件等.事实上,max-plus代数、min-max代数、完备Brouwer格、模糊代数、坡代数和瓶颈代数等都是特殊半环,如文献[2,6,22-23].可逆矩阵是一种重要的矩阵,很多学者研究了各种半环上的可逆矩阵.

众所周知,经典线性代数中可逆矩阵对矩阵方程的求解非常有用.文献[24]研究发现在交换的零和自由半环和零除子自由半环上,可逆矩阵是非常稀疏的.文献[25]给出了半可逆的概念,并得到半可逆矩阵的一些性质,得到了矩阵半可逆的必要条件和充分条件.利用这个结论,通过对矩阵方程X+A1B=A2B的讨论,从而研究了矩阵方程AX=B的解的问题.其中,A是已知的n×n阶半可逆矩阵,X是未知的n维列向量,A1和A2分别满足I+AA1=AA2和I+A1A=A2A.然而经过讨论,发现方程AX=B和X+A1B=A2B并不是在任何情况下解都相同.

为此,本文将围绕矩阵的半可逆展开详细讨论,在交换的零和自由半环上,研究矩阵方程AX=B和X+A1B=A2B在满足何种条件下才是同解的.首先给出了半可逆的定义及一些相关性质,举出方程组AX=B和X+A1B=A2B不同解的反例,同时得到方程同解的一些条件和矩阵可逆的性质,进一步概括并完善了半可逆矩阵的性质及其应用.

下面给出一些定义和已知引理.为了方便起见,用n代替集合{1,2,…,n},其中n是正整数.

定义 1.1[12]设R是一个非空集合,若在R中存在2个代数运算“+”和“·”,使得:

(i) (R,+,0)是一个交换幺半群；

(ii) (R,·,1)一个幺半群；

(iii) 任意r,s,t∈R,r·(s+t)=r·s+r·t,(s+t)·r=s·r+t·r；

(iv) 任意r∈R,0·r=r·0=0；

(v) 0≠1，

则称R=〈R,+,·,0,1,〉为半环.如果对任意r,r′∈R,都有r·r′=r′·r成立,那么称半环R是交换的.

例 1.1 设(R,+,0)是交换幺半群,若R={f:R→R,对任意a,b∈R,都有f(a+b)=f(a)+f(b)},对任意a∈R,f,g∈R,定义运算：

(f+g)(a)=f(a)+g(a),(f·g)(a)=f(g(a)),

则R是交换半环.

设R=〈R,+,·,0,1,〉是半环,若对任意a,b∈R,a+b=0蕴含a=b=0,则称半环R是零和自由的.如果对任意a∈R,存在b∈R使得ab=ba=1,则称b是a的逆.容易证明,半环上a的逆元是唯一的.用U(R)表示半环R上所有可逆元的集合.若对任意a∈R都有a∈U(R),则称半环R是半域.

例 1.2 设R是实数集,若对任意a,b∈R∪{-∞},都有

a+Rb=max{a,b},a·b=a+b

成立,其中“+”表示普通的加法,则R=〈R∪{-∞},+R,·,{-∞},0〉是交换的零和自由半环.

例 1.3 1) 设N是所有自然数构成的集合,“+”、“·”分别表示普通的加法和乘法运算,则R=〈N,+,·,0,1,〉是一个交换的零和自由半环；

2) 模糊代数([0,1],max,min)是交换的零和自由半环；

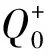
设R=〈R,+,·,0,1,〉是半环,用Mm×n(R)表示R上所有m×n阶矩阵的集合.特别地,用Mn(R)表示半环R上所有n阶方阵的集合,用Vn(R)表示R中所有n维列向量的集合.明显地,Vn(R)=Mm×1(R).设A=(aij)∈Mn×m(R),用AT=(aij)m×n表示A的转置.设

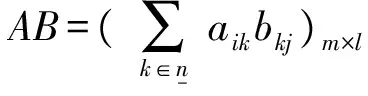
定义 1.2[5,26]设A∈Mn(R)且An(或SnAn)为{1,2,…,n}的偶(或奇)置换集合.矩阵A的双行列式|A|是一个序对|A|=(|A|+,|A|-),

其中

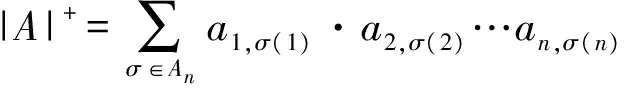
且

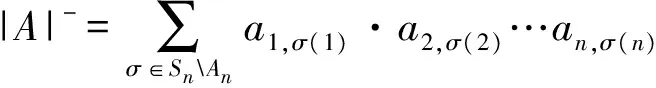
对任意i,j∈n,用Aij∈Mn-1(R)表示矩阵A删去第i行和第j列后的余子式.特别地,分别称|Aij|+和|Aij|-为矩阵A的正,负余子式[13],则

或

(1)

其中,

2 半可逆的基本定义和反例

下面给出零和自由半环上半可逆矩阵的一些基本定义和反例.

定义 2.1[12]设R=〈R,+,·,0,1,〉是半环,若对任意a,b∈R,ab=0蕴含a=0或b=0,则称半环R是零除子自由的,也称半环为整的.

引理 2.1[25]设A=(aij)∈Mn(R),则对任意r≠t,

引理 2.2[25]设A∈Mn(R)是可逆的,则|A|+≠|A|-.

定义 2.2[25]设R为零和自由半环,若对任意a≠0∈R都存在r,s∈R使得1+ra=sa,则称半环R满足条件(C).

定义 2.3[25]设R为零和自由半环,若对任意a≠b,a,b∈R都存在r,s∈R使得1+ra+sb=sa+rb,则称半环R满足条件(D).

明显地,若半环满足条件(D),则一定满足条件(C).反之,如果半环满足条件(C),则不一定满足条件(D)(参见文献[25]中的例2.3).

注 1 设半环R满足条件(D)且A∈Mn(R),若|A|+≠|A|-,则矩阵A是半可逆的.

定义 2.4[25]设A∈Mn(R),若存在A1,A2∈Mn(R)使得I+AA1=AA2且I+A1A=A2A,则称矩阵A是半可逆的.

引理 2.3[25]设半环R满足条件(D)且A∈Mn(R),若|A|+≠|A|-,则矩阵A是半可逆的.

以下例子主要说明:设A∈Mn(R),当I+AA1=AA2且I+A1A=A2A时,方程组AX=B和X+A1B=A2B不同解,其中A1,A2∈Mn(R).

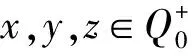
1+35r+28s=28r+35s

(2)

成立.因为半环R满足条件(D)且满足I+B1A=B2A,所以X+B1AX=B2AX,即

X+B1B=B2B.

(3)

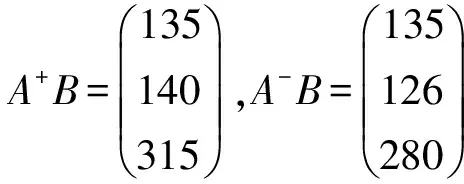
3 方程组AX=B与X+A1B=A2B同解的条件

在半环R=〈R,+,·,0,1〉上讨论方程组AX=B与X+A1B=A2B同解的条件.

分别定义矩阵A的A+和A-[18]如下：

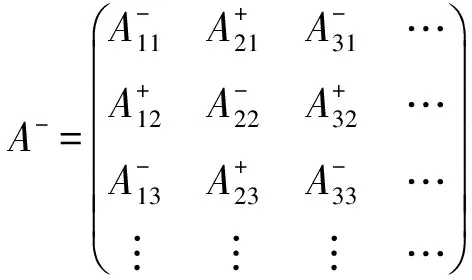
(4)

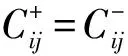
引理 3.1[18]A+A=Aδ++C,A-A=Aδ-+C,其中Aδ+和Aδ-分别是对角线上元素为|A|+和|A|-的对角矩阵.

且

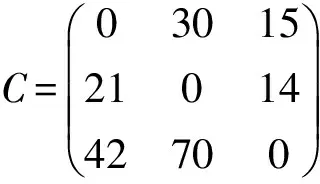
同时有

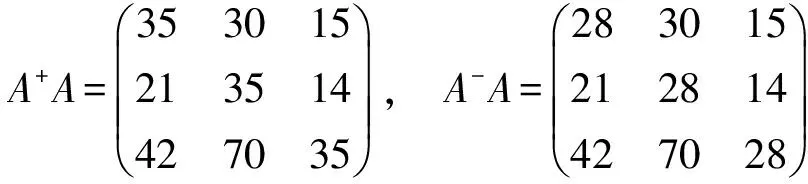
命题 3.1 设A∈Mn(R),若1+|A|+=|A|-,则A是半可逆的.

类似命题3.1可以证明以下条件成立.

命题 3.2 设A∈Mn(R),若1+|A|-=|A|+,则A是半可逆的.

定义 3.1[12]设R是半环,若ZR={x∈R:x+z=z,对任意z∈R},则称ZR是零化的.如果R=ZR,那么称R是零化半环.

定义 3.2[27]设R是半环,对任意a,b,c∈R,若a+c=b+c都有a=b,则称R是加法可消的.

命题 3.3[25]设R是半环且满足条件(D),则R要么加法可消要么零化.

下文假定B1=rA++sA-,B2=sA++rA-,αij=|Aji|(+),βij=|Aji|(-),A+=(αij)且A-=(βij),其中r,s∈R.

命题 3.4 设R是半环且满足条件(D),A∈Mn(R),若|A|+≠|A|-,则以下2个结论成立:

(i) 若R是加法可消的,则r≠s;

(ii) 若r=s,则R是零化的.

证明 由引理2.3知A是半可逆的.由定义2.4知,存在A1,A2∈Mn(R)使得I+AA1=AA2和I+A1A=A2A成立.特别地,由文献[25]中命题2.10的证明可以得到I+AB1=AB2,I+B1A=B2A.以下设B1A=(Cij)n×n,即有:

(i) 设R是加法可消的,若r=s,则B1=B2=rA++rA-,再由I+B1A=B2A可以推出I+(Cij)n×n=(Cij)n×n,即1+Cii=Cii,其中i=1,2,…,n,又因为R是加法可消的,即有1=0,矛盾,因此r≠s.

(ii) 类似(i)中证明可知:若r=s,则1+Cii=Cii,其中i=1,2,…,n,也就是说1∈Zr,故对任意x∈R,都有x+Ciix=Ciix,即R⊆Zr,又因为R⊇Zr,所以R=Zr.

然而,命题3.4的逆命题一般不成立,如例3.2所示.

注 2 设R是零化半环且满足条件(D),A∈Mn(R),|A|-≠|A|+,r,s∈R且r≠s,然而,方程组AX=B和X+B1B=B2B不一定同解(见例3.2).

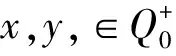
1+4r+35s=35r+4s

(5)

成立.因为半环R满足条件(D),再由I+B1A=B2A可推得X+B1AX=B2AX,即有

X+B1B=B2B

(6)

成立.由(1)和(4)式可以推出

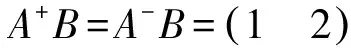
命题 3.5 设R是加法可消半环,A∈Mn(R),如果I+AA1=AA2且I+A1A=A2A,那么方程组AX=B和X+A1B=A2B同解.

证明 若存在A1,A2∈Mn(R)使得I+AA1=AA2和I+A1A=A2A都成立,则对任意X∈Mn×l(R)都有X+A1AX=A2AX,因此,由AX=B可得X+A1B=A2B.

反之,设X满足方程X+A1B=A2B,则由I+AA1=AA2知AX+AA1B=AA2B=(I+AA1)B=B+AA1B,即有AX+AA1B=B+AA1B,又因为R是加法可消的,所以AX=B.

利用命题3.1，3.2和3.5可以推出：

推理 3.1 设R是加法可消半环,A∈Mn(R),若1+|A|+=|A|-或1+|A|-=|A|+成立,则方程组AX=B与X+A+B=A-B同解.

应该注意的是：一般来说,即使半环R是零化的,方程组AX=B和X+A1B=A2B也不一定同解,其中I+AA1=AA2,I+A1A=A2A(参见例2.1).

例 3.3 设R=(N,+,·)是加法可消半环,N为自然数,“+”、“·”分别表示普通的加法和乘法运算，求:2x+z=7,3y+5z=15,x+y+2z=8,其中x,y,z∈N.

解 设

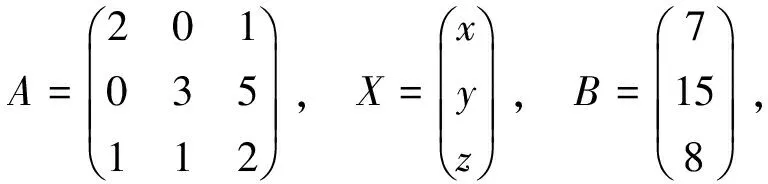
则有AX=B.

由推论3.1知|A|+=12≠13=|A|-,即A是半可逆的,因此再由定义2.4知,存在A1,A2∈Mn(R)使得I+AA1=AA2和I+A1A=A2A恒成立.特别地,由命题3.1的证明可以得到I+AB1=AB2,I+B1A=B2A,其中B1=A+,B2=A-.由I+A+A=A-A知X+A+AX=A-AX,即有

X+A+B=A-B.

(7)

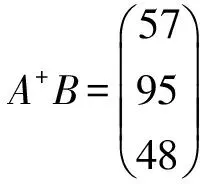
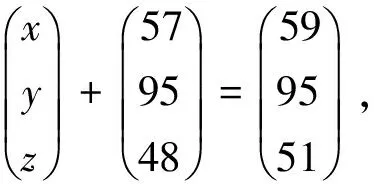
解 设

则有AX=B.由推论3.1知|A|+=9,|A|-=3,|A|+≠|A|-,则A是半可逆的.特别地,由文献[25]中命题2.10的证明可以得到:I+AB1=AB2且I+B1A=B2A,其中B1=rA++sA-,B2=sA++rA-,r,s∈R,并有

1+9r+3s=3r+9s

(8)

成立.

又因为半环R满足条件(D)且I+A1A=A2A,所以X+A1AX=A2AX,即

X+A1B=A2B.

(9)

故有

[1] BROUWER R K. A method of relational fuzzy clustering based on producing feature vectors using fast map[J]. Info Sci,2009,179(20):3561-3582.

[2] CAO Z Q, KIM K H, ROUSH F W. Incline Algebra and Applications[M]. New York:Ellis Horwood,1984.

[3] GHAZINOORY S, ESMAIL ZADEH A, KHEIRKHAH A S. Application of fuzzy calculations for improving portfolio matrices[J]. Info Sci,2010,180(9):1582-1590.

[4] GIVE’ON Y. Lattice matrices[J]. Info Control,1964,7(4):477-484.

[5] GONDRAN M, MINOUX M. Graphs Dioïds and Semirings[M]. New York:Springer-Verlag,2008.

[6] KIM K H, ROUSH F W. Generalized fuzzy matrices[J]. Fuzzy Sets and Systems,1980,4(3):293-315.

[7] NOBUHARA H, TRIEU D B K, MARUYAMA T, et al. Max-plus algebra-based wavelet transforms and their FPGA implementation for image coding[J]. Info Sci,2010,180(17):3232-3247.

[8] XU Z. A method based on distance measure for interval-valued intuitionistic fuzzy group decision making[J]. Info Sci,2010,180(1):181-190.

[9] ZHAO X Z, JUN Y B, REN F. The semiring of matrices over a finite chain[J]. Info Sci,2008,178(17):3443-3450.

[10] BACCELLI F L, MAIRESSE I. Ergodic theorems for stochastic operators and discrete event networks[J]. Idempotency,1995,11:171-208.

[11] CUNINGHAME-GREEN R A. Minimax Algebra, Lecture Notes in Economics and Mathematical Systems[M]. Berlin:Springer-Verlag,1979.

[12] GOLAN J S. Semirings and Their Applications[M]. Dordrecht:Kluwer Academic Publishers,1999.

[13] GONDRAN M, MINOUX M. Linear algebra in dioids:a survey of recent results[J]. North-Holland Mathematics Studies,1984,95(8):147-163.

[14] GONDRAN M, MINOUX M. Dioids and semirings:links to fuzzy sets and other applications[J]. Fuzzy Sets and Systems,2007,158(12):1273-1294.

[15] ZIMMERMANN U. Linear and combinatorial optimization in ordered algebraic structures[J]. Bull Am Math Soc,1985,12(1):148-150.

[16] LUCE R D. A note on Boolean matrix theory[J]. Proc Am Math Society,1952,3(3):382-388.

[17] RUTHERFORD D E. Inverses of Boolean matrices[J]. Proc Glasgow Math Association,1963,6(1):49-53.

[18] REUTENAUER C, STRAUBING H. Inversion of matrices over a commutative semiring[J]. J Algebra,1984,88(2):350-360.

[19] ZHAO C K. Inverses of L-fuzzy matrices[J]. Fuzzy Sets and Systems,1990,34(1):103-116.

[20] HAN S C, LI H X. Invertible incline matrices and Cramer’s rule over inclines[J]. Lin Alg Appl,2004,389(1):121-138.

[21] TAN Y J. On invertible matrices over antirings[J]. Lin Alg Appl,2007,423(2):428-444.

[23] CUNINGHAME-GREEN R A, BUTKOVIC P. Bases in max-algebra[J]. Lin Alg Appl,2004,389(1):107-120.

[24] BEASLEY L R B, PULLMAN N J. Linlnear operators strongly preserving idem, pot, ent matrices over semirings[J]. Lin Alg Appl,1988,99(99):199-216.

[25] GHOSH S. Matrices over semirings[J]. Info Sci,1995,90(1/4):221-230.

[26] PERFILIEVA I, KUPKA J. Kronecker-Capelli Theorem in Semilinear Spaces[M]. Computational Intelligence:Foundations and Applications,2015:43-51.

[27] WEINERT H J. Über Halbringe and Halbkörper Ⅲ[J]. Acta Mathematica Hungarica,1964,15(1):177-194.

2010 MSC： 06B15; 06D05; 03E72

(编辑 陶志宁)

Semi-invertible Matrices over Zero-sum-free Semirings

LONG Yanhua1, WANG Xueping2

(1.CollegeofTeachers,ChengduUniversity,Chengdu610016,Sichuan; 2.CollegeofMathematicsandSoftwareScience,SichuanNormalUniversity,Chengdu610066,Sichuan)

Over zero-sum-free semirings, we give an example to show that matrix equationsAX=BandX+A1B=A2Bdo not always have the same solutions, whereAis a knownn×nsemi-invertible matrix andBis an unknownn-dimensions column vector,A1andA2satisfyI+AA1=AA2andI+A1A=A2A. We present some conditions under which the systemsAX=BandX+A1B=A2Bhave the same solutions and give some properties of semi-invertible matrices. Our results extend the scope of the application of matrices.

zero-sum-free semirings; commutative semirings; semi-invertible matrix; system of linear equations; solving systems of equations

2015-06-08

国家自然科学基金(11171242)、教育部博士点基金(20105134110002)和四川省杰出青年基金(2011JQ0055)

O153.1; O159

A

1001-8395(2017)04-0450-07

10.3969/j.issn.1001-8395.2017.04.004

*通信作者简介：王学平(1965—),男,教授,主要从事不确定性的数学理论、格理论和半环上线性代数理论等方面的研究，E-mail:xpwang1@hotmail.com