完全组合作用下木-混凝土组合梁承载力计算

邱枫帆

(上海市市政工程建设处，上海市 200025)

完全组合作用下木-混凝土组合梁承载力计算

邱枫帆

(上海市市政工程建设处，上海市 200025)

木-混凝土组合梁是将木梁和混凝土梁通过剪力连接件组合到一起从而共同承担外力作用的结构体系。根据剪力连接件的抗滑移性能，木和混组合梁的连接可分为刚性连接和柔性连接。当组合梁采用刚性连接时，木梁和混凝土梁之间的相对滑移可以忽略，此时剪力连接件的连接可视为完全组合作用。根据弹性理论方法，采用应力表达的极限状态方程计算完全组合作用下木-混凝土组合梁的抗弯承载力与抗剪承载力，以期指导实际工程。

木-混凝土；组合梁；抗弯承载力；抗剪承载力；完全组合作用

0 引言

在欧、美地区，木结构、木-混凝土组合结构有着巨大的市场需求。与纯木梁相比，木-混凝土组合梁在强度和刚度等方面有着明显提升，具备较好的隔音性能；而与混凝土梁相比，木混凝土组合梁的结构自重更小，延性和抗震性能更好。

当作为受弯构件时，木梁和混凝土梁的接触面上存在纵向剪力，纵向剪力由剪力连接件承受。根据剪力连接件的抗滑移性能，木和混组合梁的连接可分为刚性连接和柔性连接。当组合梁采用粘钢、剪力隼-锚钉等刚性连接时，木梁和混凝土梁之间的相对滑移可以忽略，在计算木-混凝土组合梁此时剪力连接件的连接可视为完全组合作用[1、2]。

采用刚性连接的木-混凝土组合梁抗弯承载力和刚度较大，适合在大跨厂房、桥梁甚至高层建筑中推广使用。因此，作用在梁上的荷载强度较大时，需要对组合梁的抗弯承载力进行计算。本文根据弹性理论方法，考虑到实际工程中木-混凝土组合梁是预制构件的特点，根据一个阶段受力设计原则，采用应力表达的极限状态方程计算完全组合作用下木-混凝土组合梁的抗弯承载力，以期指导工程实际。

1 基本假设

由于木-混凝土组合梁中存在木材、混凝土、钢筋、金属连接件等材料，因此，在实际的设计过程中需要做以下几项假设：

（1）混凝土和木材均为理想的弹性材料；（2）完全组合作用下，木梁和混凝土梁之间的滑移忽略不计；（3）组合梁在受弯状态下，横截面应变成线性分布，符合平截面假定；（4）受弯状态下，木梁与混凝土梁曲率相同，不考虑混凝土板的掀起；（5）在计算混凝土梁横截面面积时不考虑钢筋的面积；（6）在跨中正弯矩作用下，不考虑混凝土梁中钢筋的作用；（7）在梁端负弯矩作用下，由混凝土梁中的钢筋抵抗拉应力（正应力）。

2 抗弯承载力计算

2.1 极限状态方程

按照弹性方法计算组合梁受弯承载力极限状态必须满足如下方程：

对于木梁，有：

对混凝土梁，有：

对于纵向受拉钢筋，有：

式中：σw为外荷载在木梁不利点处（尤其注意胶合木的指节处和枝干节点）引起的正应力，受拉为正；fw为木梁的抗拉、抗压强度设计值；σc为外荷载在混凝土梁处引起的正应力，受拉为正；fc为混凝土的抗压强度设计值；σst为外荷载引起的纵向钢筋的拉应力；fst为钢筋的抗拉强度设计值。

2.2 等效截面计算

由于忽略了木梁和混凝土梁之间的滑移，因此木梁和混凝土可以看成一个整体，可以根据材料力学的思路来分析梁单元，因此需要将混凝土梁等效为与木梁弹性模量Ew、应变εw相同的弹性截面，如图1所示，其中hw、hc、bw、bc分别为木梁和混凝土梁的高度和宽度，beq为将混凝土梁等效为木材界面后的梁宽。

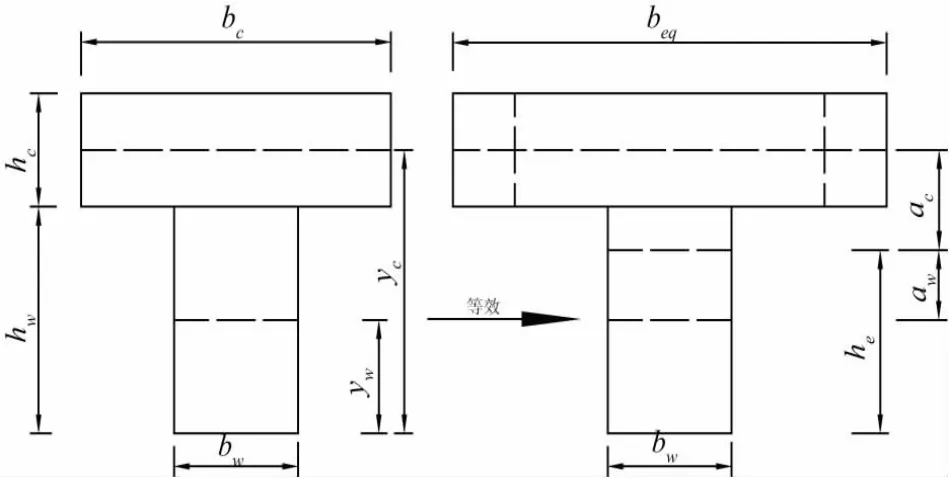
图1 组合梁截面等效示意图

根据应变相同和内力不变的原则，等效界面符合：

由式（4）和（5）可以得到：

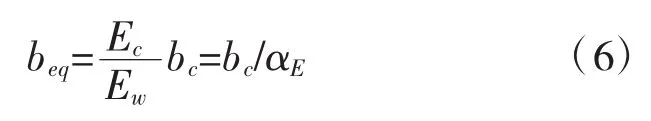
当考虑长期荷载影响时，beq=bc/（2αE）。

2.3 换算截面惯性矩计算

根据等效后的组合梁界面，确认中和轴位置为：

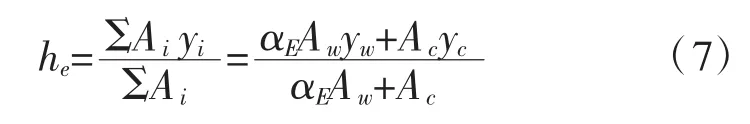
木梁形心到中和轴的距离为：

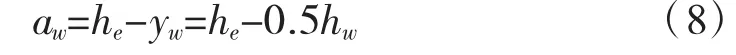
等效混凝土梁形心到中和轴的距离为：

等效截面绕中和轴的惯性矩：

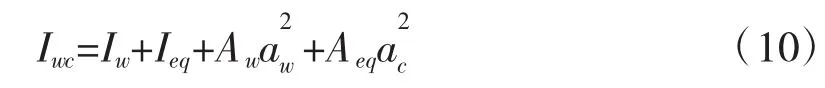
上式中Ieq=Ic/αE，Aeq=beqhc，Aw=bwhw。

2.4 抗弯承载力计算

考虑到实际工程中木-混凝土梁多为预制构件，因此与钢-混凝土组合的梁采用两个阶段受力设计方法[3]不同，在这里我们采用一个阶段受力设计。

（1）在正弯矩作用下，对混凝土梁，其最大应力为：

对木梁，截面上最大应力：

因此，正弯矩作用下，组合梁的抗弯极限承载力为式（11）、（12）的较小值：

（2）梁作为受弯构件时，梁端会出现负弯矩的作用。对混凝土梁而言，拉应力主要有钢筋承担，出于安全设计考虑，受拉区高度取到梁的上表面，因此钢筋的最大拉应力为：

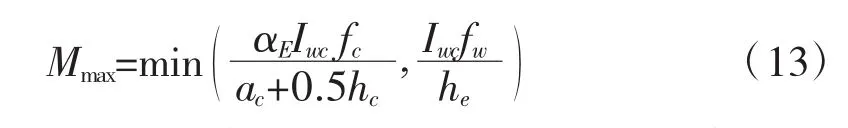
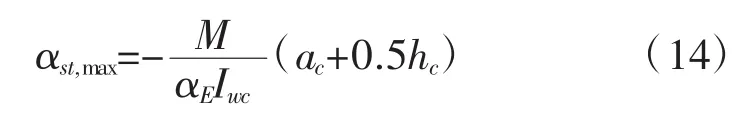
对木梁，截面上最大应力：

因此，负弯矩荷载下，组合梁的极限抗弯承载力为式（14）、（15）的较小值：

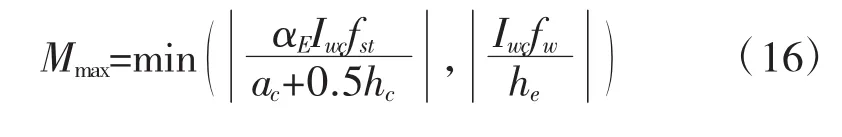
3 竖向受剪承载力计算

实际工程中，木-混凝土组合梁的除了受弯矩的作用之外，还受竖向剪力的影响。目前的试验研究[4-6]还主要停留在对组合梁受弯承载力的研究，很少有针对组合梁竖向剪力承载力的试验。因此有必要展开木-混凝土组合梁竖向受剪承载力的理论计算。

3.1 极限状态方程

按照弹性方法计算组合梁竖向受剪承载力极限状态必须满足如下方程：

对于木梁，剪应力需满足：

对混凝土梁，为了防止出现斜压破坏和大裂缝现象，必须满足如下条件：

式中：τw为木梁在竖向剪力设计值作用下的剪应力；fs为木梁的抗剪强度设计值；τc为混凝土梁在竖向剪力设计值作用下的剪应力；fc为混凝土的轴心抗压强度设计值。

此外，在进行组合梁设计时，还要根据进行横向钢筋的计算，这里不一一赘述。

3.2 抗剪承载力

与2.2节类似，考虑到大多数情况下木-混凝土组合梁多为预制构件，在这里采用一个阶段受力设计的思想进行计算分析。因此，组合梁上的竖向剪力由木梁和混凝土板共同承担。

对混凝土梁，其横截面上的最大剪应力可由下式求的：

式中，S是计算点以上换算截面对总截面的中和轴的的面积矩。

对木梁，横截面上的最大剪应力计算公式为：

因此，木-混凝土组合梁的极限抗剪承载力为式（19）、（20）的较小值：

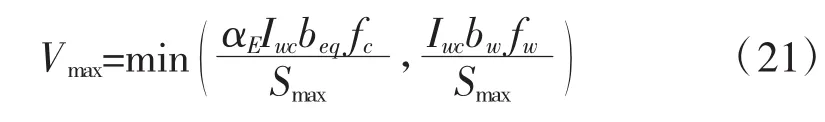
4 理论验证分析

本文根据理论的正确性，将本文计算结果和Gutkowski[7]与陈伟[8]的木-混凝土组合梁抗弯试验结果进行对比。二者分别采用剪力隼-角钢、剪力隼-螺纹钢筋作为剪力连接件。它们的共同特点是连接刚度大、抗滑移性能好，符合本文完全剪力作用的刚性连接假设。

Gutkowski[7]研究了截面为a、b两种情况的木-混凝土组合梁的抗弯承载力试验，组合梁横截面尺寸如图2所示。组合梁抗弯承载力试验采用对称四点加载法，组合梁全跨尺寸及荷载加载位置如图3所示。

图2 组合梁试件横截面示意图

图3 组合梁尺寸示意图

结合Gutkowski[7]试验中提供的数据和欧洲规范[9]的规定，图表1给出了组合梁a、b中和轴高度、惯性矩以及抗弯承载力的理论值。通过与抗弯承载力实验值的对比，可知本文的理论值偏大，但仍在在合理的范围内。

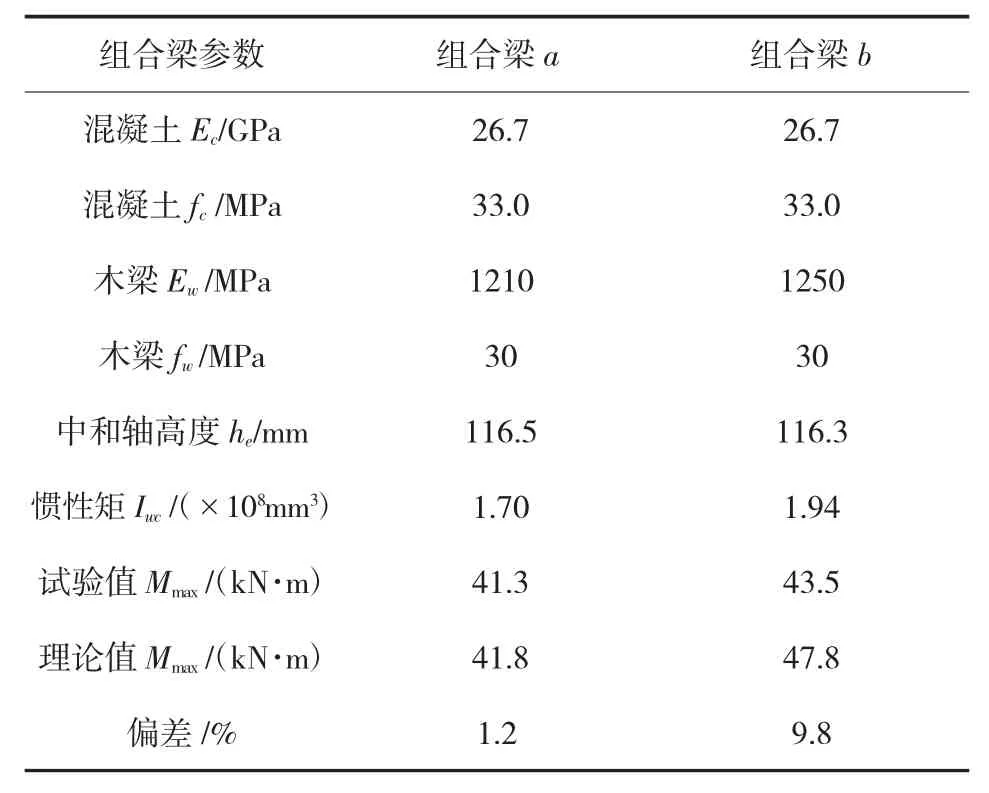
表1 组合梁抗弯承载力

陈伟[8]研究了采用剪力隼-角钢作为连接件的木-混凝土组合梁的抗弯性能和滑移特性，并分析了剪力隼间距对组合梁组合效应的影响。试验中设计了B400、B250、B200三组试件，其中数字代表剪力隼的间距（单位为mm）。由于本文理论计算采用的是完全组合作用，因此选用剪力隼较密集、抗滑移刚度较大、与本文假设模型较为相近的B250、B200进行对比计算。

表2为剪力隼间距分别为250mm和200mm时，组合梁的抗弯承载力试验值和理论值。由于组合梁B250和B200的梁截面参数和加载方式相同，因此其理论值相同。从表2中可以看出，当组合梁的剪力隼连接件间距较小时，其理论值和试验中差距较小，表明此时组合梁的连接为完全组合作用，也证明了本文理论的正确性；当组合梁的剪力隼连接件间距较大时，理论值的偏差较大，说明此时组合梁的连接为柔性连接，而本文理论采用刚性连接假设不再适用。

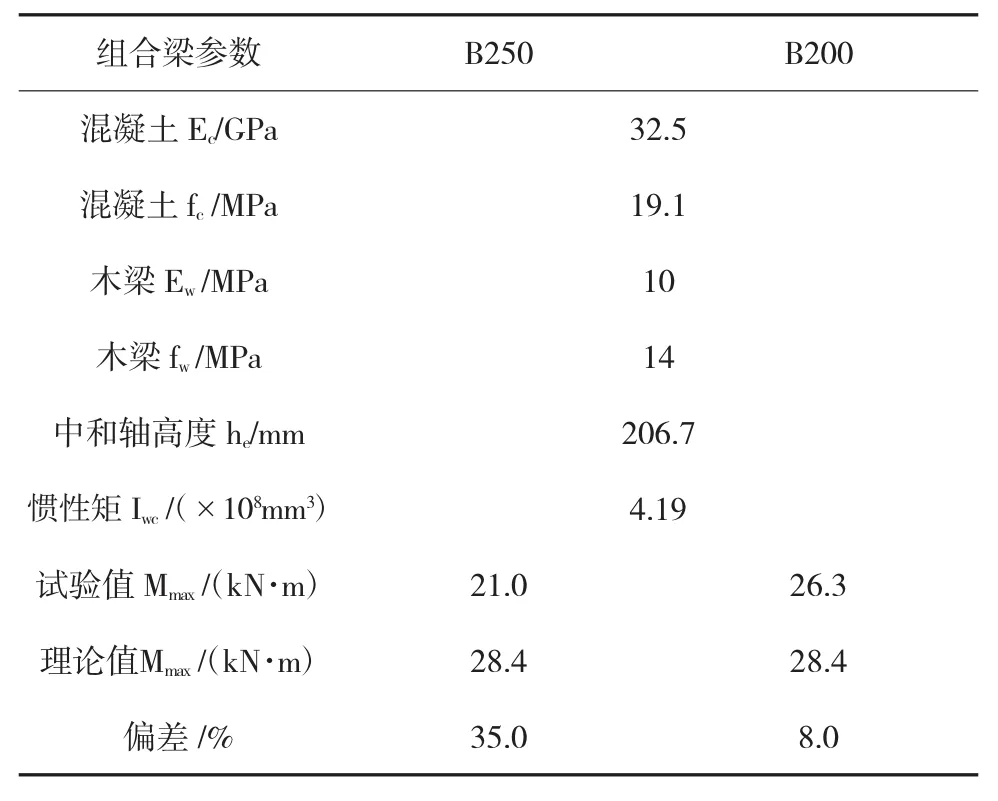
表2 剪力隼间距不同时组合梁的抗弯承载力

5 结论与展望

本文根据弹性理论方法，采用应力表达的极限状态方程对采用刚性连接件的完全组合作用下的木-混凝土组合梁进行分析，并得到了组合梁正、负弯矩的极限抗弯承载力和极限抗剪承载力的计算方法，为设计木-混凝土组合梁提供了理论基础。此外，将本文理论结果与Gutkowski[7]和陈伟[8]的试验结果进行对比，证明了本文理论的正确性。

本文的推导基于强度极限状态分析，而在实际工程中，木梁的弹性模量较小、变形较大，因此有必要进一步研究木-混凝土组合梁的变形控制条件。此外，本文的极限抗弯、抗剪承载力是基于梁的尺寸和材料（木、混凝土）参数，并未考虑连接件间距、锚入深度等因素的影响，有必要展开刚性连接件相关参数对抗弯、抗剪承载力的影响分析。

[1]俞宏,宋林,吴文清.木-混凝土组合梁剪力连接件研究现状[J].世界桥梁,2014,(6):61-67.

[2]王斌,肖飞.木-混凝土组合梁剪力连接件研究现状综述[J].江苏建筑,2012,(3):42-43.

[3]陈忠汉,胡夏闽.钢混凝土组合结构设计[M].北京:中国建筑工业出版社,2009.

[4]胡夏闽,李巧,彭虹毅,陆伟东.木-混凝土组合梁静力试验研究[J].建筑结构学报,2013,(S1):371-376.

[5]SáRibeiro R A,SáRibeiro M G.Composite Wood–Concrete Structural Floor System with Horizontal Connectors[J].International Journal of Concrete Structures and Materials,2015,9(1):61-67.

[6]Yeoh D,Boon K H,Loon L Y.Timber-Concrete Composite Floor Beams under 4 Years Long-Term Load[J].International Journal of Integrated Engineering,2013,5(2).

[7]Gutkowski R,Brown K,Shigidi A,et al.Laboratory tests of composite wood-concrete beams. Construction and Building Materials,2008,22(6):1059-66.

[8]陈伟.工程木—混凝土组合梁受力性能分析与试验研究[D].长沙:中南林业科技大学,2016.

[9]European Committee for Normalization,Eurocode 5(2003)-Design of timber structures-Part 1-1:General-Common rules and rules for buildings,Final Draft,prEN 1995-1-1(Bruxelles,Belgium).

TU318.1

B

1009-7716（2017）08-0275-04

10.16799/j.cnki.csdqyfh.2017.08.087

2017-06-01

邱枫帆（1971-），男，上海人，本科，工程师，主要从事工程建设项目建设管理。