FRP加固木梁受弯承载力与挠度研究

，，,

(1.西南科技大学 土木工程与建筑学院，四川 绵阳 621010；2.西南科技大学 文学与艺术学院，四川 绵阳 621010)

木结构是我国传统建筑中最为重要的结构形式之一，目前，我国木结构仍广泛应用.木材质量较轻，顺纹强度较高，但由于天然缺陷和环境因素的影响，定期的维护和加固是必不可少的.纤维增强复合材料(FRP)具有轻质、高强的特点和优越的抗腐蚀性能，用于木结构加固可以克服传统加固方法的缺点[1-3].美、日等国家最早用FRP加固修复木结构，Plevris与Triantafillou[4]从单向纤维布加固木梁的抗弯性能试验中发现，木梁经纤维布加固后其承载力、刚度和延性等方面均有非常大的提高.Borri[5]对20根FRP加固旧木梁进行四点弯曲试验，并根据Bazan[6]模型建立起木梁的极限承载力公式和数值计算方法,对比试验结果，发现两者吻合较好，建议使用Bazan本构模型进行计算.Chen[7]在研究FRP加固木梁时，分析了Neely[8]模型和Bazan[6]模型存在的缺点，提出Chen应力-应变模型.国内祝金标[9]对FRP加固破损木梁进行了试验研究，试验表明CFRP对木梁有良好的加固效果.谢启芳[10-11]总结了木梁受弯破坏模式，发现梁底粘贴CFRP布能提高木梁抗弯承载力与刚度，但提高程度不高，主要因为控制木梁破坏的是木纤维的极限抗拉强度，而纤维布的强度优势得不到发挥.可见，已有的研究成果对于FRP加固木梁破坏模式、承载力提高以及改善木梁脆性破坏方面达成共识，但在FRP加固木材计算模型仍有待深入研究，Neely的理想弹塑性模型精度较差，Bazan模型比较接近木材真实的应力-应变行为，但用作计算过于复杂；谢启芳和Chen的模型类似，虽然谢启芳的模型更符合实际，但在满足计算准确度的情况下，Chen模型用于计算更为方便快捷，以便更广泛应用.

笔者基于Chen提出的木材等效最大压应力本构模型，理论推导并建立FRP加固木梁的受弯承载力和挠度的计算公式，并进行CFRP加固木梁抗弯承载力试验，以试验结果验证理论公式计算的可靠性，为今后FRP加固木梁的工程设计提供理论依据.

1 FRP加固木梁受弯承载力分析

1.1 基本假定

只考虑木梁受弯，忽略剪力影响，平截面假定成立；木材的受拉和受压弹性模量相同；忽略FRP布厚度影响；木梁与FRP布之间不发生粘结滑移；木材的应力—应变关系采用Chen模型，见图1(a)，碳纤维布采用线弹性模型，见图1(b).

图1 木材和碳纤维布的应力-应变模型

Chen应力—应变模型[7]表达式为

(1)

FRP布的应力-应变曲线可表达为

(2)

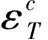
1.2 全过程受弯承载力理论分析

图2为木梁受弯时典型的M-δ曲线，共分为两个阶段.当荷载较小时，木材和FRP都处于弹性阶段，该阶段可用材料的强度理论进行分析，直到压区木纤维达到等效最大应力时，阶段Ⅰ终止.阶段Ⅱ始于压区纤维屈服，终止点可能是拉区纤维被拉断、压区纤维被压皱或是FRP被拉断.大量试验表明：拉区木纤维拉断和压区木纤维压皱是FRP加固木梁常见的两种受弯破坏模式，FRP拉断破坏很少发生[11].

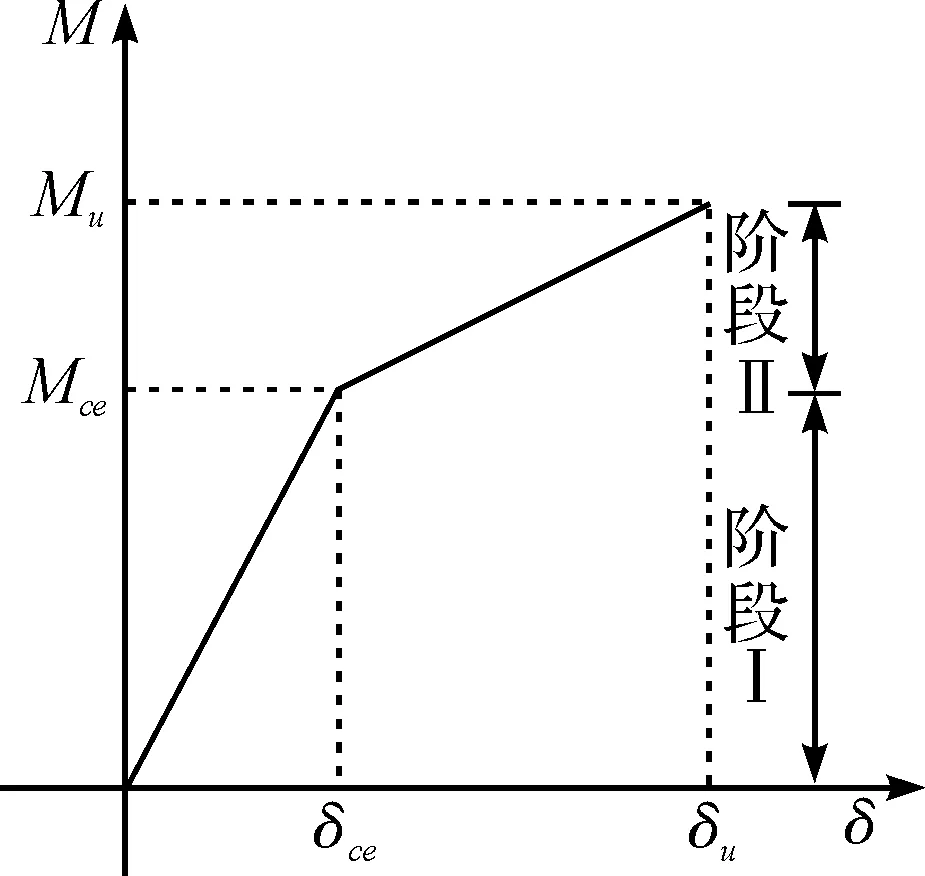
图2 木梁受弯M-δ曲线

1.2.1 阶段Ⅰ—木材和FRP处于弹性阶段

(3)

则截面惯性矩为

(4)

根据经典弯曲理论，木梁截面上的最大拉、压应力分别为

(5)

FRP上的应力为

(6)

在阶段Ⅰ，FRP加固木梁压区木纤维达到等效最大压应力时的极限弯矩承载力为

(7)

对于未加固梁，取纤维布面积AF=0，即为未加固木梁截面上相应的应力和承载力.

式(3—7)中：AF为FRP布截面面积；b,h,c分别为木梁宽度、高度和截面压区高度；n为FRP与木材弹性模量之比；M为荷载作用下的弯矩；I1为木材和FRP处于弹性阶段时的截面惯性矩；δ为木梁跨中挠度；Mce为木材压区木纤维达到弹性极限压应变时木梁弯矩.

1.2.2 阶段Ⅱ—压区木纤维进入塑性阶段

阶段Ⅱ，加固木梁压区进入塑性阶段，M-δ曲线斜率发生变化.阶段Ⅱ有可能发生拉区木纤维拉断破坏或压区木纤维压皱破坏.

1) 拉区木纤维拉断破坏.当木纤维达到极限拉应变时，根据截面变形协调关系和力平衡条件则可建立FRP加固木梁的极限承载力计算公式，图3(a)为计算简图.

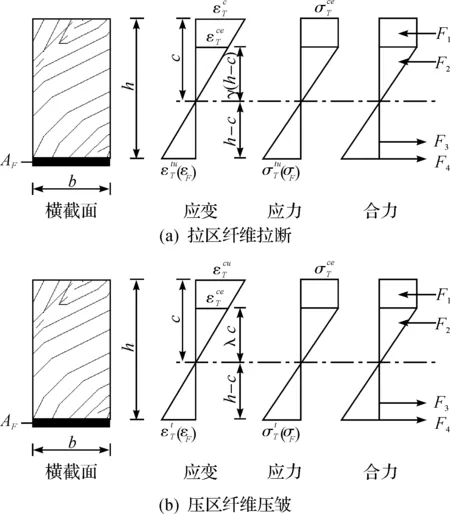
图3 极限承载力计算简图

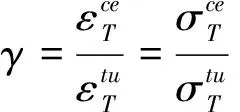
(8)

木梁正截面拉区木纤维拉力F3和FRP布拉力F4分别为

(9)

由木梁正截面静力平衡条件可知

F1+F2=F3+F4

(10)

式中：F1,F2分别为木纤维压区弹性压力和塑性压力；F3,F4分别为木梁拉区木纤维拉力和FRP布拉力.将式(8，9)代入式(10)得

(11)

故FRP加固木梁发生受拉木纤维拉断破坏时的截面压区高度表达式为

(12)

则FRP加固木梁的极限弯矩承载力为

(13)

(14)

则，木梁正截面压区弹性压力F1和塑性压力F2分别为

(15)

木梁正截面拉区木纤维拉力F3和FRP布拉力F4分别为

(16)

将式(14—16)代入式(10)得

(17)

由式(17)便可解得FRP加固木梁发生受压木纤维压皱破坏时的截面压区高度c.

故极限弯矩承载力为

(18)

其中λ为木材压区弹性极限压应变与木材极限压应变之比.

在阶段Ⅱ中，1)和2)两种破坏模式的承载力计算公式取ρF=0时，即为未加固木梁的受弯极限承载力.

2 FRP加固木梁抗弯全过程挠度计算理论分析

图2中木梁受弯时的M-δ曲线分为两个阶段，木梁挠度计算则应分阶段计算.针对常见的两点集中荷载作用下木梁跨中挠度进行分析.此时，木梁跨中挠度为

(19)

式中：a,l分别为木梁的剪跨比和净跨.

2.1 阶段Ⅰ—木材和FRP处于弹性阶段

当木材和FRP处于弹性阶段时，先通过式(3，4)计算出加固木梁的截面惯性矩I1，再将I1代入式(19)，即可求出加固木梁在弹性阶段的挠度.阶段Ⅰ压区木纤维达到等效最大压应力时，木梁跨中挠度公式为

(20)

式中：δce为压区木纤维达到等效最大压应力时的木梁跨中挠度；Me为压区木纤维达到等效最大压应力时的木梁的弯矩.

2.2 阶段Ⅱ—压区木纤维进入塑性阶段

在阶段Ⅱ，由于木梁截面压区纤维进入了塑性阶段，不能再用阶段Ⅰ的弹性模量ET进行挠度计算.因此，可先计算弹性区和塑性区对中性轴的弯曲刚度，再合成为总的弯曲刚度[10].

1) 拉区纤维拉断破坏.图4(a)为拉区纤维拉断破坏时的弯曲刚度计算简图.

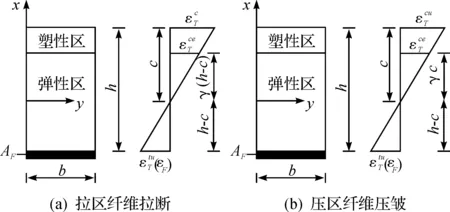
图4 弯曲刚度计算简图

木纤维弹性区的弯曲刚度为

(21)

FRP换算弯曲刚度为

(22)

木纤维塑性区弯曲刚度为

(23)

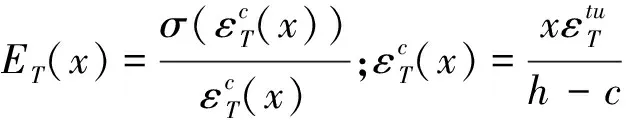
(24)

总的弯曲刚度为

(25)

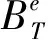
2) 压区木纤维压皱破坏.图4(b)为压区纤维被压皱破坏时弯曲刚度计算简图.

木纤维弹性区的弯曲刚度为

(26)

FRP换算弯曲刚度同式(23).由于压区木纤维达到了极限压应变，近似取塑性区模量为弹性极限应变和极限压应变模量的平均值，则木纤维塑性区弯曲刚度为

(27)

故任意弯矩M作用下，FRP加固木梁在阶段Ⅰ和阶段Ⅱ过程中的挠度可以线性插值的方法得到

(28)

式中δu为木梁的极限跨中挠度.

(29)

Chen对《Wood handbook》中22种不同木材进行强度的线性回归分析，得出μ=0.93.因此，当没有木材足够数据的情况下，可取μ=0.93进行计算.

3 试验研究及对比分析

3.1 全过程受弯承载力理论分析

本试验共制作了三根木梁，木梁尺寸及FRP布粘贴层数、厚度见表1.选用的碳纤维布(CFRP)为东丽UT70-20，厚度为0.167 mm，弹性模量为214 GPa，极限抗拉强度为3 430 MPa.结构胶采用B&803，抗剪强度为37 MPa.基于材性试验[12-13]测得木材顺纹抗拉强度为46 MPa，顺纹抗压强度为18.4 MPa，弹性模量为8.2 GPa.在粘贴CFRP之前先用砂纸去除木梁底部多余的木纤维，用结构胶将凹凸不平的表面填平，接着在梁底涂上结构胶，再CFRP布沿木梁顺纹方向粘贴，为防止CFRP与木梁剥离破坏，粘贴U型箍，如图5，6所示.

表1 木梁尺寸及纤维布粘贴层数表

图5 木梁加载简图

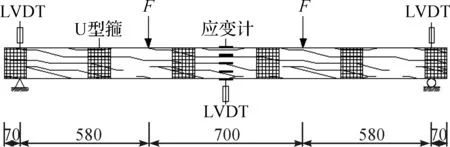
图6 测点布置图

试验共计3个工况，第一组不进行任何形式加固，作为参照对比梁，编号TB0，第二组木梁底部全跨顺纹粘贴一层CFRP布，编号TB1，第三组木梁底部全跨顺纹粘贴两层CFRP布，编号TB2.木梁采用两点集中加载方式进行抗弯承载力试验，先对试件进行预加载，加载采用匀速单调加载，加载共分10～20级，每级持荷3～5 min.

本试验中三根木梁均发生受拉木纤维拉断坏，表2为各工况木梁的极限承载力和挠度的试验结果，采用一层CFRP加固木梁，极限承载力提高了8.7%，两层CFRP加固木梁极限承载力提高24.7%.同时，CFRP加固木梁减小了木梁极限状态时的跨中的挠度，加固一层跨中极限挠度减小了12.5%，加固二层跨中极限挠度减小了15.1%.对比加固一层和两层的木梁，挠度减小并不够显著，因此纤维布的配布率的增加对的木梁的截面刚度提高不明显，说明单独依靠增加配布率并不能有效地改善木梁的变形.

表2 木梁的极限承载力和跨中挠度

3.2 全过程受弯承载力理论分析

本试验中三根木梁均发生拉区木纤维拉断破坏，基于试验木梁及CFRP布物理参数，采用笔者所建立的理论计算公式进行CFRP加固木梁的抗承载力和挠度计算，并与试验值对比，如表3,4所示.可见CFRP加固木梁承载力理论计算值与试验值吻合较好，挠度计算理论值与试验值有一定偏差，这可能跟近似计算塑性区模量、木材的内部的缺陷以及不均匀性有关.

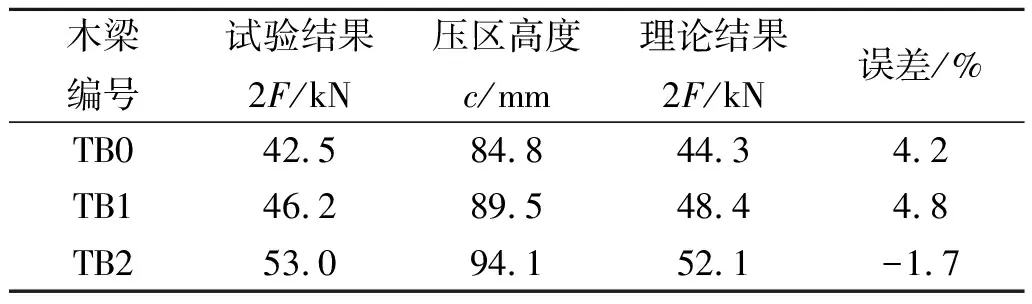
表3 极限承载力的理论值与试验值

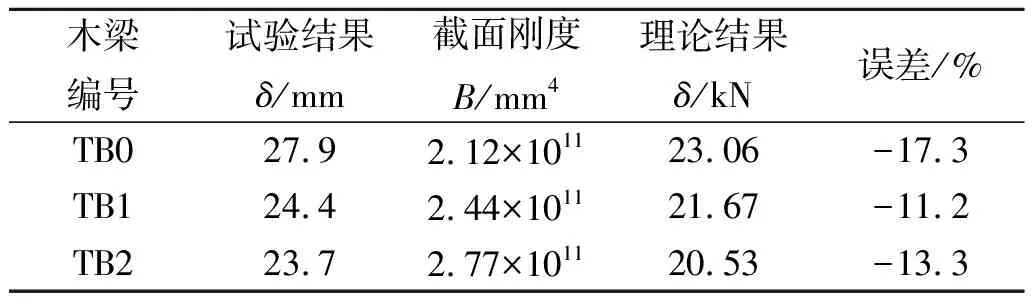
表4 极限跨中挠度的理论值与试验值

4 结 论

根据木梁受弯时典型的M-δ曲线，对两种常见破坏模式下FRP加固木梁的弹性阶段和弹塑性阶段进行了全过程分析.基于木材Chen本构模型，建立了FRP加固木梁在弹性极限和弹塑性破坏时的受弯承载力和挠度公式.对三根木梁进行了抗弯性能试验，结果表明：三根试验木梁均发生受拉木纤维拉断破坏，随着配FRP布率增加，木梁破坏时的荷载明显增大，说明粘贴FRP布能有效提高木梁极限承载力；随着配FRP布率的增加，木梁的挠度呈减小趋势，但减小并不够显著，因此纤维布的配布率的增加对木梁的截面刚度提高不明显，说明单独依靠增加配布率并不能有效地改善木梁的变形.通过建立的理论公式，计算出的各木梁极限承载力和跨中挠度，并与试验结果对比，承载力计算结果与试验值吻合较好，挠度值存在一定偏差，这可能跟近似计算塑性区模量、木材的内部的缺陷以及不均匀性有关，还需进行更深入的研究.

参考文献：

[1] 许清风，朱雷.FRP加固木结构的研究进展[J].工业建筑，2007,37(9)：104-180.

[2] 马建勋，蒋湘闽，胡平，等.碳纤维布加固木梁抗弯性能的试验研究[J].工业建筑，2005,35(8)：35-39.

[3] 梁正洪，杨俊杰.CFRP加固大偏压RC柱二次受力时的机理分析[J].浙江工业大学学报，2010,38(4):458-461.

[4] PLEVRIS N, TRIANTAFILLOU T C. FRP-reinforced wood as a structural material[J]. Journal of Material in Civil Engineering,1992,4(3)：300-317.

[5] ANTONIO B, MARCO C. A method for flexural reinforcement of old wood beams with CFRP materials [J]. Part B，2005，36：143-153.

[6] BAZAN IM. Ultimate bending strength of timber beams [D]. Halifax, NS, Canada：PhD Thesis. Nova Scotia Technical College,1980.

[7] CHEN Yong-xian. Flexural analysis and design of timber strengthened with high strength composites [D]. PhD Thesis: New Brunswick Rutgers, the State University of New Jersey,2003.

[8] NEELY S T. Relation of compression-endwise to breaking load of beam [J]. Progress in Timber Physics, USDA,1898,18:13-17.

[9] 祝金标，王柏生，王建波.碳纤维布加固破损木梁的试验研究[J].工业建筑，2005,35(10):86-89.

[10] 谢启芳.中国木结构古建筑加固的试验研究和理论分析[D].陕西：西安建筑科技大学，2007.

[11] 谢启芳,赵鸿铁,薛建阳,等.碳纤维布加固木梁正截面抗弯承载力的计算[J].建筑结构，2008,38(5):76-79.

[12] 中华人民共和国住房和城乡建设部.GB/T 50329—2012 木结构试验方法标准[S].北京：中国建筑工业出版社，2012.

[13] 中华人名共和国建设部.GB 50005—2003 木结构设计规范(2005版)[S].北京：中国建筑工业出版社，2006.