梁格法建模在宽箱梁桥静载试验中的应用

邵样林

（东莞市交业工程质量检测中心，广东 东莞 523125）

梁格法建模在宽箱梁桥静载试验中的应用

邵样林

（东莞市交业工程质量检测中心，广东 东莞 523125）

梁格法是一种空间计算分析的方法，具有清晰、易理解等特点，广泛引用到宽桥、异形桥等的计算分析。在桥梁静载试验理论分析中，它能得到主要控制截面的挠度、应变数据，以满足宽箱梁桥静载试验的理论计算要求。基于梁格法理论，采用空间梁格法对某连续宽箱梁桥进行分析，计算分析了设计活载静载响应，得出主要控制截面的横向测点理论计算值，并根据现场静载试验结果对该桥进行评估。对梁格法在桥梁静载试验应用中提供了借鉴和参考。

梁格法；静载试验；宽箱梁桥

0 引言

随着交通运输的蓬勃发展，尤其是高速公路，城市立交的增多，各种结构形式复杂的桥梁也随之出现。为了满足交通运输快速顺畅的要求，斜桥、宽桥、弯桥等复杂的桥梁得到广泛的引用。而在桥梁设计、交竣工检测中，桥梁上部结构受力分析比一般直桥、窄桥复杂的多。目前在桥梁内力建模计算的方法有单梁法、板单元法、实体单元法、梁格法等。单梁法的特点是能直接计算结构的内力和变形，在计算窄桥和直桥的时候很方便快捷且准确度高；而在计算宽跨比比较大的桥时有很大的局限性，宽桥梁不能满足基本假定。其次该方法不能满足桥梁的横向受力分布。在桥梁检测时，特别是宽桥的静载检测中，必须检测桥梁的横向受力分布情况。采用单梁模型，不管车道如何布置，如何进行偏载计算，对其正力都是没有影响的，对于弯矩在各腹板的受力是无法体现的。在桥梁的检测中，特别是偏载加载的时候，桥梁的横向受力不均的，要得到桥梁横向分布测点的计算的理论值，采用梁格模型计算，更能合理接近结构的实际受力。板单元和实体单元法在桥梁检测工况多的时候，计算工作量比较大，计算繁琐，模型复杂，数据处理繁琐，其应用受到限制。梁格法在计算宽桥、斜弯桥不仅有效，而且经济，结构提取方便。对其选择合适的分析方法进行分析，不仅能够反映结构的真实受力，在偏载作用下，结构受力的真实情况、横向受力分布等，而且能控制质量和造价，对各个腹板的受力配筋有一定的指导作用。

1 梁格法的基本理论

梁格法的基本思路是将桥梁的上部结构用一个等效的梁格来模拟，将桥梁上部结构模拟成若干个等效梁格。将分散在原板梁和箱梁每个区段的抗弯刚度和抗扭刚度集中于最邻近的梁格内，使实际结构纵向刚度集中在模型的纵向梁格上，横向刚度集中在模型的横向梁格内，再对形成的“空间梁格”施加荷载分析。梁格划分必须满足等效原则：承受相同的荷载时，实际结构和所划分的梁格所产生的挠度曲线应该是相同的，而且每个梁格内的弯矩、剪力、扭矩应该等于所代表实际结果部分的内力。采用梁格法建模时，梁格的建模非常重要，划分得合理，所用的梁格模型和实际结构受力就非常吻合。划分得不恰当，所用的模型受力就偏离实际结构的受力，给实际结构设计和检测所需理论值带来错误的影响。由于实际结构和梁格体系在结构上的差异，使得这种等效只是近似的。梁格的划分，截面的选取必须满足以下几个要求：

（1）为了得到每条腹板各个截面的设计弯矩和设计剪力，在每条腹板处设置纵向单元。为了加载的方便，特别是在桥梁检测偏载加载时，需在悬臂端部设置虚拟的纵向单元,纵梁抗扭刚度的计算按整体箱型断面自由扭转刚度平摊到各纵梁上。

（2）梁格的纵向杆件形心高度位置应尽量与箱梁截面的形心高度相一致，纵横杆件的中心与原结构梁肋的中心线相重合，使腹板剪力直接由所在位置的梁格构件承受。

（3）横向单元应与纵向单元垂直。一般在跨中、1/4跨、1/8跨、支座处、横格梁处设置横向单元。横向单元的间距直接决定了荷载在纵向单元之间的传递，间距过大会使相邻纵向单元间的力产生很大跳跃；间距太密又会大大增加工作量，也毫无必要。为保证荷载的正确传递，最大间距不能超过相邻两个反弯点间距的1/4，在支点的附近应适当加密,横向梁格的间距根据不同位置有所不同，墩顶和跨中的则要根据桥梁的实际情况调整。

2 梁格法建模在宽箱梁桥检测实例分析

2.1 工程概况

某高速公路跨铁路桥梁，桥梁跨径为58 m+ 105 m+58 m，半幅桥梁宽16.5 m，桥梁上部结构采用变截面结构形式，采用单箱双室。设计活载是公路-Ⅰ级。桥梁立面图、平面图、横截面图分别见图1、图2和图3。

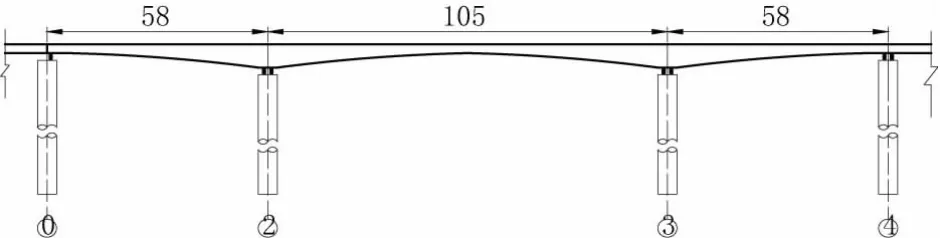
图1 立面图（单位：m）

图2 平面图（单位：m）

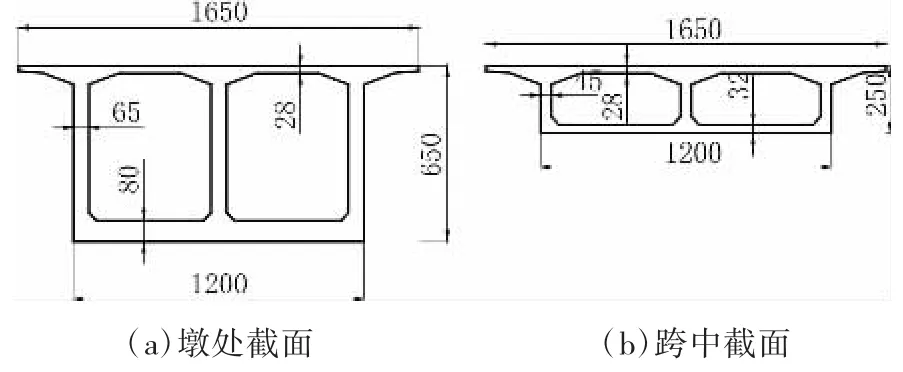
图3 桥梁横截面图（单位：cm）

2.2 桥梁模型

2.2.1 单梁模型

对该桥梁分别用单梁进行分析，见图4所示。得出该桥在设计活载作用下的弯矩包络图，见图5所示。在设计活载作用下，第一跨0.45L、中跨0.5L、第三跨0.55L弯矩最大，可知桥梁试验的截面位置和加载位置分别为主跨的跨中位置、主墩附近位置、边跨0.45L位置。可知边跨在设计活载作用下最大正弯矩为252 40 kN·m。

图4 单梁模型

图5 设计活载弯矩包络图（单位:kN·m）

2.2.2 梁格模型

（1）箱梁截面的划分如图6所示，梁格纵向杆件的中性轴的位置尽量保持和箱梁的刚度一致,由于该桥的箱梁是单箱双室，因此在设计梁格截面时，以腹板作为每片梁的代表。本试验根据桥梁的实际情况设计了梁格空间杆系模型,如图7所示。

图6 梁格纵梁划分

图7 空间梁格杆系模型

（2）一般情况下，横向梁格间距根据不同位置而有所不同，本桥边跨主桥的梁格间距为5.6 m，主跨的梁格间距为10.3 m，墩顶横梁根据桥梁实际情况进行调整。该宽度的抗扭刚度惯性矩计算公式为[1]：

公式的字母代表如图8所示。

图8 梁格构件示意图

根据图6可知，每片腹板梁的抗弯特性与纵向梁格截面相同，同时在设计墩顶横梁和跨中横梁刚度时，应该将横隔板的作用列入考虑范围，使其横梁刚度更具有合理性。该宽度的抗扭刚度惯性矩计算公式为[1]：

在箱梁的空间设计时应考虑横隔板的作用，若横隔板无法承受箱梁箱室的重力，就会造成顶板和底板变形弯曲，各腹板也会出现不同程度的弯曲变形，而腹板为竖向方向箱梁，其单位宽度等效剪切面积可根据以下公式计算[2-4]：

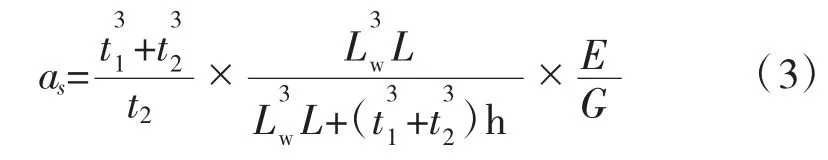
箱梁截面梁格的划分、横隔梁格间距的选取以及横隔板结构尺寸的选取至关重要。选取的合理，所计算的理论值与实际结构受力相符合，便能为箱梁静载试验提供理论基础。

2.3 桥梁静载试验及分析

2.3.1 静载理论分析

桥梁设计软件Madia/Civil2012对该桥梁格法进行建模，利用动态规划加载法得出1#肋梁在设计活载下弯矩包络图，如图9所示。在设计活载作用下，1#肋、2#肋、3#肋在边跨弯矩最大总和为245 60 kN·m，与单梁模型比较误差值为（25240-24560）/25240×100%=0.27。

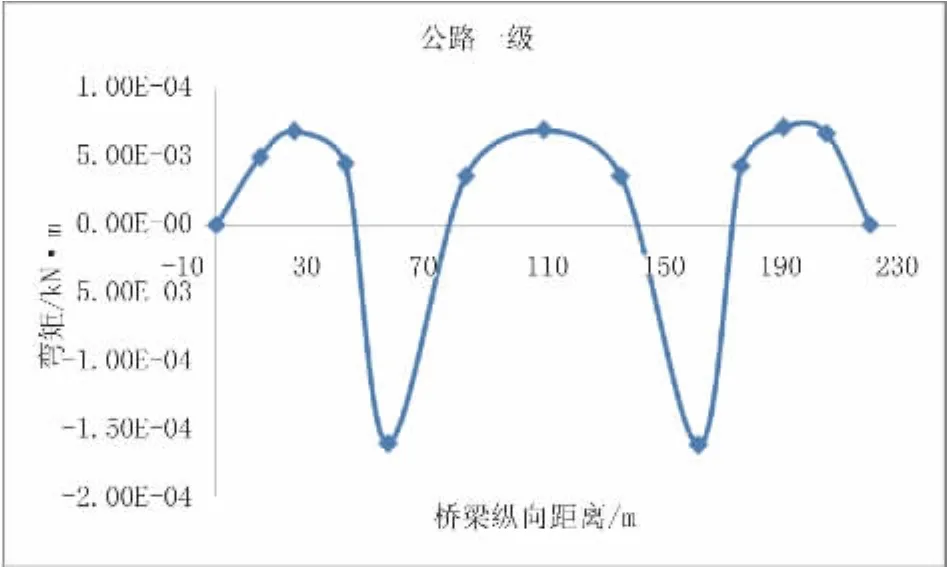
图9 1#肋纵梁在设计活载下的弯矩包络图

2.3.2 测试截面和测点布置

根据的活载作用下的弯矩包络，静载试验分3个工况进行。工况1测试的截面为主跨跨中截面最大正弯矩（A截面），工况2为主墩附近最大负弯矩（B截面），工况3为边跨0.55L截面最大正弯矩（C截面）。本次试验需要10台约350 t的重车，加载平面图见图10，测点分布如图11所示，工况1-工况3截面应变测点如图12所示。

图10 静载车辆加载平面图（单位：m）

图11 挠度测点分布平面图（单位:m）

图12 各工况截面应变测点示意图

2.3.3 静载试验结果分析

（1）挠度测试：工况1和工况3作用下，主要测点在满载测试结果见表1，横向测点在满载时测试值与理论值比较图见图13。

表1 主要测点挠度满载测试结果（单位：mm）

图13 工况1和工况3满载实测值和理论值比较图

（2）应变测试：在各个工况满载下，测出梁底各个肋梁应变值以及腹板的应变测点值。工况1和工况3主要测点满载测量值和理论值见表2。工况2作用下腹板测点应变值见表3。梁底测点（各肋梁测点）在满载下测量值和理论值比较图见图14。腹板测点在工况2满载下，应变沿梁高的变化图见图15。

表2 梁底主要测点在满载应变测点 με

表3 工况2腹板主要测点满载测试结果 με

图14 工况1和工况3满载梁底横向测点实测值和理论值比较图

图15 工况2腹板测点应变测量值

在工况1试验荷载作用下，3-1#测点（1#肋梁）最大弹性挠度12.25 mm，对应的理论计算值为18.65 mm，校验系数为0.66。A1、A2（1#肋梁）最大弹性应变为60 με，对应的理论计算值为90 με，校验系数为0.67；在工况3试验荷载作用下，7-1#测点（1#肋梁）最大弹性挠度5.35 mm，对应的理论计算值为8.55 mm，校验系数为0.63，C1、C2（1#肋梁）最大弹性应变为32 με，对应的理论计算值为43 με，校验系数为0.74。以上挠度和应变均满足《公路桥梁荷载试验规程》（JTG/TJ 21-01-2015）校验系数的要求且小于0.8，表明该桥具有一定的刚度和安全储备[5]。该桥墩处截面中性轴高度为3.0063，通过图15可得出该桥实际截面中性轴高度为2.996 m，基本与设计相符合。

由上述结果可知，各试验工况下，采用梁格法计算的挠度和应变横向分布曲线与实测曲线趋势较为一致，说明该桥在刚度取值以及梁格截面的划分较为合理。采用梁格法分析为箱梁静载试验横向测点提供理论数据，有上述结果（校验系数）可以看出试验测出的数据普遍偏小，笔者认为该桥桥面铺装了10 cm的沥青混凝土，梁格模型分析时未考虑桥梁铺装层对桥梁整体刚度的影响。

3 结 语

（1）梁格法是一种能较好的模拟原结构空间受力的分析方法，对于宽箱梁桥在桥梁检测中，特别是采用偏载法时，采用梁格法建模可以较为准确的反映箱梁各个腹板的受力情况和桥梁的横向分布。为桥梁检测横向测点分布提供有效的理论依据，能满足箱梁桥静载试验理论的要求，在工程界得到广泛应用。梁格模型和单梁模型理论计算值差值较小，表明箱梁的梁格模型能够满足桥梁静载检测的要求。

（2）实测数据变化趋势与理论数据较吻合，说明采用梁格模型能较好的模拟宽箱梁在偏载试验下的空间受力特点，整个受力工作状态都能反映出来。

（3）从试验数据和理论计算数据比较分析得出的校验系数偏小，建议在静载试验理论分析建模的时候，考虑二期恒载对桥梁整体结构刚度的影响。一般建模的时候将箱梁的顶板加厚，但这样使得箱梁截面的中性轴整体上移给计算带来一定的误差，一般是在梁格模型上加入板单元来考虑铺装层的影响。

[1]蒋丽飞,孙卓.基于梁格法的宽箱梁桥静动载试验评估[J].广东土木与建筑,2010，7（7）：11-13.

[2]刘刚城.梁格法在某单箱双室连续箱梁纵向分析中的应用[J].铁道勘察与设计，2002（5）：18-20.

[3]戴公连，李德建.桥梁结构空间分析设计方法与应用[M].北京:北京人民交通出版社，2001.

[4]范立础.桥梁工程[M].北京:人民交通出版社，1996.

[5]JTG/TJ21-01-2015,公路桥梁荷载试验规程[S].

U446

A

1009-7716（2017）08-0262-04

10.16799/j.cnki.csdqyfh.2017.08.083

2017-04-15

邵样林（1985-），男，江西鹰潭人，硕士研究生，路桥工程师，从事路桥检测工作。